Рассмотрим взаимосвязь дифференциала, плеча и эффекта финансового рычага: ЭФР=ДИФ∙ПФР. На практике дифференциал и плечо могут быть взаимозависимыми. Действительно, каждый очередной кредит увеличивает плечо и, соответственно, увеличивается риск невозврата. Поэтому банк даёт его под больший процент. Как следствие, растёт стоимость заёмного капитала, дифференциал уменьшается. Но есть доводы и в пользу независимости: хорошее обеспечение кредита (залоги, поручительства и т.п.), использование различных внешних источников.
Проанализируем влияние дифференциала и плеча на ЭФР в предположении, что они независимы друг от друга. На рисунке 4.2 построены две убывающие ломаные линии. Это зависимости плеча финансового рычага ПФР от дифференциала ДИФ для значений эффекта финансового рычага 5 и 10%. Другими словами – это линии равного уровня для ЭФР в координатах ДИФ и ПФР. То, что они убывают – естественно: например, для обеспечения ЭФР=5% при увеличении ДИФ требуемое значение ПФР снижается, и наоборот: при уменьшении дифференциала требуемое значение плеча растёт.
Рассмотрим проблему финансового риска на конкретном учебном примере. Для удобства обозначим: Р – функция риска, Д – дифференциал, П – плечо, Э – эффект рычага. Введём три функции риска с некоторым обоснованием их вида:
· Р1=К1/(Д+1) (чем больше дифференциал, тем меньше риск невозврата – обратная зависимость, гиперболическая функция); К1 и К2 – ниже - коэффициенты пропорциональности, весовые коэффициенты, с помощью которых из двух функций риска составится одна – их «свёртка»;
· Р2=К2∙П (чем больше плечо, тем больше риск невозврата заёмного капитала – прямая зависимость, линейная функция, );
· Р=Р1+Р2=К1/(Д+1) + К2∙П (это функция суммарного риска, «свёртка»).
Будем измерять степень риска (или просто риск) по 100-бальной шкале в процентах, считая риск в 100% категорически недопустимым. На этом основании методом проб и ошибок определяем эмпирические значения коэффициентов: К1=51, К2=17. Наша функция риска примет конкретный вид:
| Р=51/(Д+1) + 17∙П | (4.9) |
Плечо (ПФР)
3 Риск=60%
Риск=45%
Риск=30%
1 ЭФР=10%
ЭФР=5%
Риск-15%
3 6 9 12 ДИФ, %
Рисунок 4.2 Номограмма: взаимосвязь дифференциала, плеча,
эффекта финансового рычага и финансового риска
На рисунке 4.2 каждая точка на плоскости имеет четыре координаты: дифференциал, плечо, эффект и риск.
Построим линии равного риска в координатах Д и П (дифференциал и плечо для риска Р равного 15% (малый риск), 30, 45, 60% (значительный риск). На рисунке 4.2 эти функции представлены возрастающими ломаными линиями равного уровня, идущими снизу-вверх и слева-направо.
Пример 4.6.Для риска Р=30% запишем функцию риска:
51/(Д+1) + 17∙П=30.
Отсюда следует функция линии равного уровня:
П=(30-51/(Д+1) (1/17).
Окончательно, зависимость плеча от дифференциала для 30% риска примет вид:
П=1.76-3/(Д+1).
Функция риска начинается в углу нашего квадранта, эта точка соответствует риску 30%, но ЭФР здесь близок к нулю. Чтобы повысить эффект, переместимся по линии риска вправо-вверх, увеличивая при этом как дифференциал, так и плечо. Линия риска пересекает сначала линию эффекта 10% в точке с координатами (примерно) Д=4 и П=1.1. Если нас такой эффект не устраивает, двигаемся по лини риска 30% дальше до пересечения с линией эффекта 10%. Здесь точка пересечения имеет координаты: дифференциал Д=7% и очень большое плечо П=1.4. Например, П=ЗК/СК=14 млн.руб/10 млн.руб = 1.4).
Конец примера 4.6.
Пример 4.7. Пусть экономическая рентабельность активов (ЭРА) предприятия 19%, стоимость заёмного капитала 16%. Определить, при каком плече и риске можно достигнуть эффекта рычага 10%.
Решение. 1) найдём дифференциал ДИФ=19-16=3%.
2) используем рисунок 4.2, из точки с координатами (3, 0) поднимаемся вертикально до пересечения с линией ЭФР=10%; эта точка имеет координаты: плечо П=3, риск Р 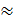 70%, что можно трактовать как большой риск.
70%, что можно трактовать как большой риск.
3) предложение. Для достижения эффекта в 10% желательно постараться увеличить дифференциал, например, до 5%. Тогда для достижения эффекта в 10% необходимо, чтобы прибыль П=2, соответствующий риск будет приемлемым, примерно 38%.
Конец примера 4.7.
Вывод 1. Рисунок 4.2 и пример 4.7 наглядно показывают, что высокого эффекта финансового рычага нельзя достигать только увеличением плеча - наращиванием заимствованных средств - без превышения разумного риска. Для перехода на линию большего эффекта при том же риске требуется значительно увеличить дифференциал и лишь незначительно «позволяется» увеличить плечо.
Вывод 2. Для конкретного предприятия и конкретных условий менеджер должен построить собственную номограмму, со своими коэффициентами К1 и К2 и даже со своими функциями риска. Со временем их нужно «подстраивать».
Вывод 3. На основе выводов 1 и 2 и должна строиться рациональная заёмная политика, политика привлечения внешних финансовых источников, которую можно кратко выразить так: ЭФР 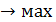 при Риск(ЭФР) при Риск(ЭФР) 
|
Вопросы для самоконтроля к 4.2.
1) Приведите доводы как в пользу зависимости дифференциала и плеча финансового рычага, так и в пользу их независимости.
2) Какие доводы можно привести в пользу обоснования трёх введённых функций риска (ответ строить как комментарий к соответствующим формулам)?
3) Какие поправки к функциям риска вы бы предложили для устранения их «дефектов»?
4) Дайте определение понятию: линия равного уровня.
5) Каким образом точка на плоскости (см рисунок 4.2) соответствует четырём координатам; как это связано с понятием «номограмма».
6) Почему высокого эффекта финансового рычага нельзя достигать только увеличением плеча, ответ обоснуйте с использованием рисунка 4.2.
7) В чём состоит рациональная заёмная политика, дайте развёрнутый ответ (в том числе с возможностью сделать дифференциал и плечо независимыми).
Дата: 2016-10-02, просмотров: 343.