Задачи начисления процентов
Финансовому менеджеру приходится формировать кредитную политику. Для этого необходимо уметь ориентироваться в задачах начисления процентов.
В таблице 3.1 представлены четыре способа начисления процентов при финансовых расчётах.
Таблица 3.1 Классификация способов начисления процентов
| Тип процентной ставки | Способ начисления процентов | |
| Декурсивный | Антисипативный | |
| Простой | 1 Простые ставки ссудных процентов | 2 Простые учётные ставки |
| Сложный | 3 Сложные ставки ссудных процентов | 4 Сложные учётные ставки |
3.1.1 Простые ставки ссудных процентов (ССП).При декурсивном способе проценты начисляются (уплачиваются) по истечении каждого интервала начисления (квартала, года) по отношению к первоначальной сумме. Отсюда следует:
| i = (S-P)/P | (3.1) | |
| где: | i – ставка ссудного процента; | |
| S – наращенная сумма; | ||
| P – первоначальная сумма; | ||
| S–P – процентная сумма. |
Выведем основную формулу для начисления процентов. Пусть вклад (депозит) внесён в банк на три года с ежегодным начислением процентов по годовой ставке i, например, 0,20 (20%). . Тогда по истечении трёх лет вкладчик получит: S = Р + iP +iP + iP= Р(1+3i). Отсюда основная формула для наращенной суммы:
| S=P(1+n∙i) | (3.2) |
Если период начисления процентов задан в днях, то (3.2) примет вид:
| S=P(1+(д/К)i) | (3.3) |
| где | д и К | – число дней в периоде начисления процентов и в году соответственно. |
При начислении процентов используются определённые «практики», см таблицу 3.2.
Таблица 3.2 Практики начисления процентов
| Практика | Вид процентов | Число дней ссуды |
| Германская | Обыкновенные (год = 360 дней) | Приближенное (любой месяц = 30 дней) |
| Французская | Точное (месяц = 28/29, 30, 31 день) | |
| Английская | Точные (год = 365/366 дней) |
Пример 3.1. АО «Алмаз» получает кредит в 50 млн.руб на 1.5 года по годовой простой ставке ссудного процента 18%. Определить наращенную сумму (которую общество должно вернуть банку) и сумму процентных денег.
Решение. 1) Наращенная сумма S=P(1+n∙i)=50(1+1.5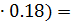 
63.5 млн.руб.
2) Сумма процентных денег = 63.5 - 50= 13.5 млн.руб.
Пример 3.2. Кредит в 10 млн.руб выдан АО «Альфа» на срок со 2 марта и до 11 июля по годовой простой ставке ссудного процента 15%, год високосный. Определить наращенные суммы для германской и английской практик начисления.
Решение. 1) Для германской практики S=P(1+(д/К)i) = 10(1 + 0.15 
129/360) = 10.537500 млн.руб.
2) Для английской практики S=P(1+(д/К)i) = 10(1 + 0.15 132/366) = 10.540983 млн.руб.
3.1.2 Простые учетные ставки.При антисипативном (предварительном) способе проценты начисляются по отношению к наращенной сумме и предъявляются к оплате в начале каждого интервала. Это имеет значение, например, при высокой инфляции. Из сказанного следует:
| d=(S-P)/S | (3.4) |
где d – простая учётная ставка.
В общем виде аналоги формул (3.2) и (3.3) будут иметь вид:
| P = S-D
Р = S(1 - n d)=
Р = S(1- (д/K)d)
| (3.5) | ||
| где | S – наращенная сумма; она должна быть возвращена банку; | ||
| P –сумма, получаемая заёмщиком; | |||
| D = S – P – дисконт, общая сумма процентных денег; | |||
| d – простая годовая учётная ставка. |
Пример 3.3. АО «Гамма» берёт кредит на 2 года по простой учетной ставке 20%. Требуется возвратить 55 млн.руб. Рассчитать а) сумму, которую получит заемщик, б) величину дисконта.
Решение. а) Сумма, которую получит заёмщик Р=55(1 - 2 
0.2)=33 млн.руб.
б) Дисконт D=S-P=55 - 33=22 млн.руб.
3.1.3 Сложные ставки ссудных процентов.Сложная ставка отличается от простой тем, что проценты за каждый очередной период «капитализируются», то есть, прибавляются к телу кредита и на эту сумму начисляются проценты за очередной период. Выведем основную формулу. Пусть вклад (депозит) внесён в банк на три года с ежегодным начислением процентов по сложной годовой ставке iс, например, 0,20. Выражения для наращенных сумм будут иметь вид:
за 0 лет S0 = P;
за 1 год S1 = P + icP;
за 2 года S2 = (P + icP) + (P + icP)ic = P(1 + ic)2
за 3 года S3 = P(1 + ic)2 + P(1 + ic)2ic = P(1 + ic)3
Отсюда нетрудно записать основную формулу:
| S=P(1+∙iс)n | (3.6) |
Если сложные проценты начисляются несколько раз в году, например, поквартально, то (3.6) запишется так:
| Smn=P(1+j/m)mn | (3.7) | ||
| где | m – | число равных интервалов начисления в году (при поквартальном начислении m=4) | |
| j – | номинальная годовая ставка ссудного процента, например, 0.20 | ||
| j/m - | Ставка ссудного процента на интервале внутри года (квартальная) |
Если срок ссуды n не целое число, то используют приближенный способ вычислений:
| S ≈ P(1+ ic)nа(1+nb ic) | (3.8) | ||
| где | na – | целое число лет от n | |
| nb – | остаток – дробная часть года от n, n=na+nb |
На рисунке 3.1 показаны наращивание суммы как процесс во времени для простых и сложных ставок ссудных процентов (декурсивное начисление).
S Сложные проценты
Простые проценты
Р
1 2 3 4 n
Рисунок 3.1 Процессы наращивания сумм
Пример 3.5.АО «Факел» положило на депозит 450 тыс.руб под 18% годовых. Определить 1) наращенную сумму через 3 года для простых и сложных ставок ссудных процентов, 2) то же при начислении процентов по полугодиям.
Решение. .1). для простой ставки имеем S=450(1+3*0.18)=693 тыс.руб; для сложной ставки S=450(1+0.18)3 =739.364 тыс.руб.
2). При начислении по полугодиям: а) для простой ставки результат не изменится, б) для сложной ставки S = 450(1 + 0.18/2)2 3 
754.695 тыс.руб.
Пример 3.6. АО «Вест» положило на депозит 450 тыс.руб на 2 года и 4 месяца под сложные 18% годовых с начислением по полугодиям. Определить приближенно наращенную сумму.
Решение. Используем формулу (3.8): S = 450(1+0.18/2)2 2(1+(0.18/12) 
) = =450 
1.094 1.06 = 673.324 тыс.руб.
В заключение приведём таблицу 3.3 с формулами начисления процентов.
Таблица 3. 3 Шесть формул для определения наращенной суммы
| 1 Простая ставка ссудного процента | S=P(1+n∙i) |
| 2 Простая учётная ставка | S=P/(1-nd), получено из P=S-D=S(1-nd) |
| 3.1 Сложная ставка ссудного процента, m=1 3.2 Сложная ставка ссудного процента, m>1 | Sn=P(1+ ic)n Smn=P(1+j/m)mn |
| 4.1 Сложная учётная ставка, m=1 4.2 Сложная учётная ставка, m>1 | Sn=Р/(1- dс)n S=P/(1-f/m)mn |
3.1.4 Эквивалентные процентные ставки.Эквивалентными называются такие ставки i и d, применение которых при одинаковых условиях дают одинаковые финансовые результаты. Для их нахождения используют уравнение эквивалентности: S1(i)=S2(d). Отсюда можно вывести формулы для каждой из ставок:
| i=f(d) и d=φ(i) | (3.9) |
Выведем конкретный вид формул (3.9) для простых ставок при декурсивном и антисипативном способах начисления. Для этого используем формулы из 1-й и 2-й строк таблицы 3.3. Запишем уравнение эквивалентности: P(1+n∙i)= P/(1-nd). Из него находим:
| i=d/(1-n d); d=i/(1+n i).
| (3.10) |
Пример использования идеи эквивалентности ставок см в 3.2.2 и (3.12).
Пример 3.8.Годовая ставка ссудного процента i=0.17, период начисления 2 года. Определить эквивалентную ей учётную ставку.
Решение. Используем 2-ю формулу из (3.10): d = 0.17/(1+2∙0.17) ≈ 0.13. Вывод: если в банке предложат на выбор кредит по ставкам i=17% либо d=14%, то выгоднее выбрать первое.
Вопросы для самоконтроля к 3.1.
1) В чём суть декурсивного и антисипативного способов начисления процентов?
2) Как проявляются различия в типах процентных ставок: простой и сложной?
3) В чём суть метода капитализации процентов по депозиту?
4) Чем отличается германская практика начисления процентов от французской?
5) Как выглядит уравнение эквивалентности процентных ставок?
Дата: 2016-10-02, просмотров: 302.
