ЛИНЕЙНЫХ ДИФФЕРЕНЦИАЛЬНЫХ
УРАВНЕНИЙ
Решение линейных дифференциальных уравнений операционным методом предполагает три этапа: 1) переход от исходных функций к их изображениям по Лапласу, при этом дифференциальное уравнение преобразуется в алгебраическое относительно изображения искомой функции; 2) решение полученного алгебраического уравнения; 3) получение искомого решения по его изображению.
Рис. 44.1
Решим Задачу Коши для дифференциального уравнения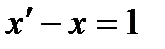 
при начальном условии x(0)=1. Операционный метод решения такой задачи состоит в том, что искомую функцию и правую часть дифференциального уравнения считаем оригиналами и переходим от уравнения, связывающего оригиналы, к уравнению, связывающему их изображения. Воспользуемся формулой дифференцирования оригинала 
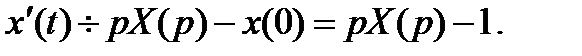Применяя свойство линейности, перейдём в уравнении 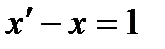от оригинала к изображениям: 
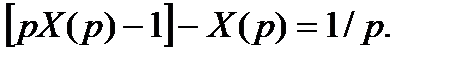Решим полученное уже не дифференциальное, а алгебраическое уравнение относительно неизвестного изображения X(p): 
Осталось по неизвестному изображению X(p) найти соответствующий ему оригинал x(t). Используя свойство линейности преобразования Лапласа и табличные операционные соотношения, получаем 
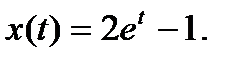Это и есть искомое решение задачи Коши. Аналогично решаются системы линейных дифференциальных уравнений.
Формула Дюамеля
Рассмотрим линейное дифференциальное уравнение n-го порядка с постоянными коэффициентами:
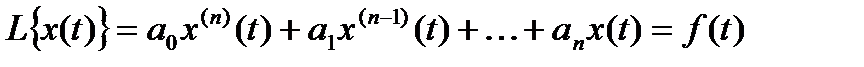
при нулевых начальных условиях
| . |
| ) |
| ( |
| ) |
| ( |
| ) |
| ( |
| ) |
| ( |
| = |
| = |
| = |
| ¢ |
| = |
| - |
| n |
| x |
| x |
| x |
| … |
(Заменой искомой функции задачу с ненулевыми начальными условиями можно свести к задаче с нулевыми условиями.). Допустим, что известно решение уравнения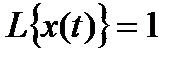 
(с той же левой частью и правой частью, равной единице) при нулевых условиях. Обозначим его 
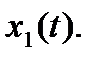Тогда решение x(t) задачи Коши можно выразить через 
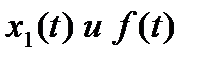с помощью одной из формул:
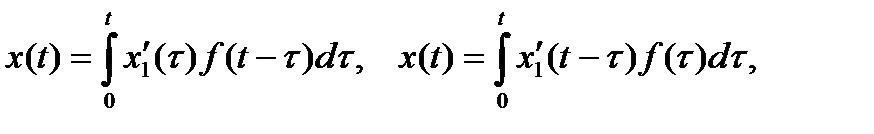
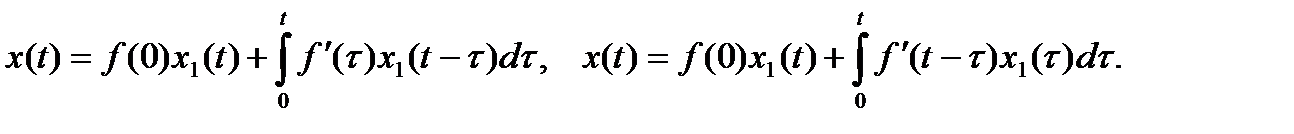
Каждое из этих выражений называют формулой (или интегралом) Дюамеля. Метод решения дифференциальных уравнений, основанный на формуле Дюамеля, применяют, как правило, в тех случаях, когда возникают трудности при нахождении изображения F(p) правой части f(t) , а также при необходимости многократного решения задачи для различных функций f(t)
Пример 1 .На материальную точку массы m действует сила сопротивления R = kv, пропорциональная скорости. Какое расстояние пройдёт точка за неограниченное время, если ей сообщена начальная скорость v0 ? k = m, v0 = 7 м/с.
Решение: Исходя из второго закона Ньютона: am= - kv,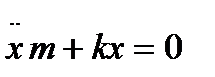 
. Начальные условия: 
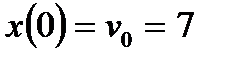, x (0) = 0. Подставим значения k: 
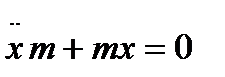. Сократим все выражения на m: 
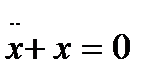. Перейдём к изображениям функций:
p 2 X (p) – px (0) – x (0) –pX(p) – x (0) = 0,
p (p+1)X (p) – 7 = 0, p (p+1)X (p) = 7
X (p) =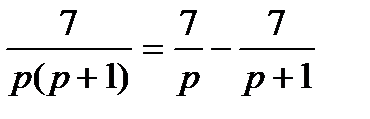 
По такому изображению легко найти оригинал:
x (t)=7 – 7 e -t .
Пример 2 .Найти решение задачи Коши
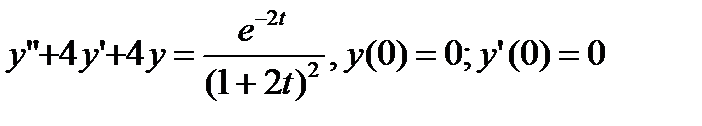
Решение: Вначале решим вспомогательную задачу
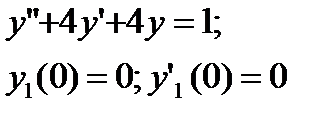
Если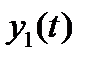 
соответствует изображение 
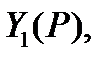то переходят от оригиналов функций к их изображениям, получим
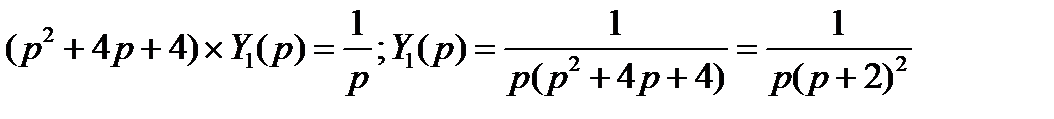
Разложим дробь на простые дроби, получим
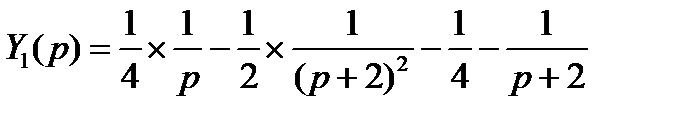
По таблице оригиналов .
Найдем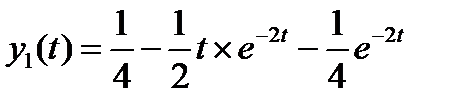 
Используя формулу Дюамеля, получим искомое решение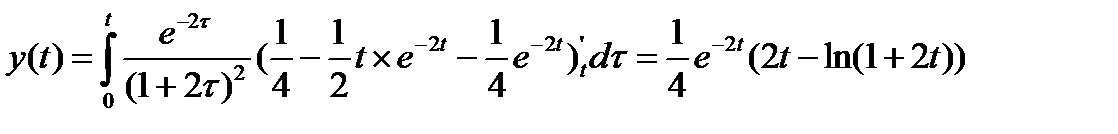 
ЗАКЛЮЧЕНИЕ
В настоящем пособии рассмотрены лекции по разделам «Математика». Издание рекомендуется вместе со стандартными задачами по высшей математике для работы на практических занятиях, а также при выполнении типовых расчетов и при составлении комплексных заданий, аттестационных контрольных работ по указанным темам.
Авторы считают, что пособие поможет более глубокому и полному усвоению студентами материала по данным в пособии разделам и будет соответствовать эффективной организации учебного процесса по курсу «Математика» для студентов инженерно-технических специальностей.
Библиографический список
1. Бугров, Я.С. Элементы алгебры и аналитической геометрии / Я. С. Бугров, С. М. Никольский. – М.: Дрофа, 2006. – 192 с.
2. Беклемешев, Д.В. Курс аналитической геометрии и линейной алгебры / Д. В. Беклемешев. – М.: Наука, 2005. – 320 с.
3. Головина, Л.И. Линейная алгебра и некоторые ее приложения / Л. И. Головина. – М.: Наука, 1979. – 390 с.
4. Клетеник, Д.В. Сборник задач по аналитической геометрии / Д. В. Клетеник. – М.: Наука, 2007. – 333 с.
5. Данко, П.Е. Высшая математика в упражнениях и задачах / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. – Ч. 1. – М.: «Оникс 21 век», 2007. – 368 c.
6. Данко, П.Е. Высшая математика в упражнениях и задачах / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. – Ч. 2. – М.: «Оникс 21 век», 2007. – 416 c.
7. Сборник задач по математике для втузов. В 4 ч. Ч. 1. Линейная алгебра и основы математического анализа / под ред. А.В. Ефимова, А.С. Поспелова. – М.: Физматлит. 2004. – 462 с.
8. Кузнецов, Л.А. Сборник заданий по высшей математике (типовые расчеты)/ Л.А. Кузнецов. – СПб.: Лань, 2008. – 240 c.
9. Шипачев, В.С. Основы высшей математики / В.С. Шипачев. – М.: Высшая школа, 2003. – 479 с.
10. Катрахова, А.А. Элементы линейной алгебры и аналитической геометрии : учеб. пособие/ А.А. Катрахова, Г.Ф. Федотенко. – Воронеж. ВГТУ, 2008. – 161c.
11. Пискунов, Н. С. Дифференциальное и интегральное исчисление / Н. С. Пискунов.– Т.1.– М.:Символ плюс, 2007.–416 с.
12. Катрахова, А. А. Дифференциальные уравнения и их приложения: учебное пособие / А.А. Катрахова, Г.Ф. Федотенко. – Воронеж. ВГТУ, 2009 . –146 с.
13. Краснов, М.А. Функции комплексного переменного. Операционное исчисление. Теория устойчивости / М.А. Краснов, А.И. Киселев , Г.И. Макаренко - М.: 1981. – 204 с.
14. Пискунов, Н. С. Дифференциальное и интегральное исчисление /Н. С. Пискунов.–Т.2.–М.:Символ плюс, 2007.–544 с.
15. Чудесенко, В.Ф. Сборник заданий по специальным курса высшей математики. Типовые расчеты / В.Ф. Чудесенко. –
СПб.: Лань, 2007. –126 с.
16. Фихтенгольц, Г.М. Основы математического анализа / Г.М. Фихтенгольц. – Т. 1. – СПб.: Лань, 2008. – 440 c.
17. Фихтенгольц, Г.М. Основы математического анализа / Г.М. Фихтенгольц. – Т. 2. – СПб.: Лань, 2008. – 464 c.
18. Будак, Б.М. Кратные интегралы и ряды / Б.М. Будак, С.В. Фомин. – M.: Наука, 1967. – 608 c.
19. Лунгу, К.Н. Сборник задач по высшей математике. 2 курс / К.Н. Лунгу, В.П. Норин, Д.Т. Письменный, Ю.А. Шевченко. – М.: Айрис- пресс, 2004. –592 c.
20. Эльсгольц, Л.Э. Дифференциальные уравнения / Л.Э. Эльсгольц. – М. : Ком. Книга, 2006. – 272 с.
21. Бугров, Я.С. Высшая математика. Задачник / Я. С. Бугров. – С. М. Никольский. – М.: Дрофа, 2006. – 253 с.
22. Бугров, Я.С. Дифференциальное и интегральное исчисление / Я. С. Бугров. – С. М. Никольский. – М.: Дрофа, 2006. – 432 с.
23. Бугров, Я.С. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексной переменной / Я. С. Бугров. – С. М. Никольский. – М.: Дрофа, 2006. – 464 с.
24. Катрахова, А. А. Лекции по теории комплексного переменного и операционному исчислению: учебное пособие / А.А. Катрахова, М.П. Семенов. – Воронеж. ВГТУ, 2004 . – 120 с.
25. Катрахова, А. А. Ряды Фурье и их применение в решении
задач математической физики и обработки информации: учебное пособие / А.А. Катрахова, Е.М. Васильев, В.С. Купцов, А.В. Купцов. – Воронеж. ВГТУ, 2010 . – 216 с.
26. Катрахова, А. А. Кратные интегралы. Векторный анализ: учебное пособие / А.А. Катрахова, В.С. Купцов, А.В. Купцов . – Воронеж. ВГТУ, 2006. –97 с.
оглавление
Введение…………………………………………….…………...3
1. Определители, матрицы. Системы линейных уравнений….3
2. Линейные пространства. …………………………………......28
3. Подпространства, образованные решениями линейной
однородной системы (лос) уравнений. Нахождение общего
решения лос………………………………………………...…….36
4. Линейные преобразования и действия над ними ………….39
5. Собственные значения и собственные векторы
матрицы…………….................................................................….41
6. Приведение квадратичной формы к каноническому
виду………………………………………………………………45
7. Векторы и действия над ними …………………………...….48
8. Плоскость и прямая в пространстве………………………… 52
9. Кривые второго порядка на плоскости………………...…...57
10. Приведение общего уравнения кривой второго порядка
к каноническому виду…………………………………...……. 60
11. Исследование общего уравнения кривой.
Поверхности второго порядка.……………………….……..….61
12. Комплексные числа. Теорема Безу. Числовая
последовательность и ее предел ………………..….……..…...77
13. Функция. Предел функции……………………………..… 87
14. Применение эквивалентных бесконечно малых
к вычислению пределов ………………….…………………….101
15.Производная функции и ее вычисление …………………...106
16 Дифференциал функции. Применение дифференциала…..110
17. Неопределенный интеграл ………………………………..132
18. Определенный интеграл…………...……….…………... ...139
19. Несобственные интегралы …………………………….. ...141
20. Приложения определённого интеграла ………………......144
21. Функции нескольких переменных основные
теоретические сведения …………..…………………………..154
22. Частные производные первого порядка. Полный
дифференциал функции и его применение
к приближенным вычислениям …………………….………159
23. Производные и дифференциалы высших порядков ….168
24. Формула Тейлора для функции двух переменных…… 175
25. Экстремум функции нескольких независимых
переменных……………………………………………………176
26. Условный экстремум. Наибольшее и наименьшее
значения функции в замкнутой области …………………...183
27. Дифференциальные уравнения ………………………...189
28. Система линейных дифференциальных уравнений
второго порядка с постоянными коэффициентами …………204
29. Числовые ряды…………….…………………………….....207
30. Функциональные ряды ……………………………………218
31. Тригонометрические ряды Фурье ………………………..232
32. Интеграл Фурье …………………………………………..263
33. Двойной интеграл ………………………………………..272
34.Тройные интегралы……………………………………... ..289
35. Криволинейные интегралы ……………………………….302
36. Поверхностные интегралы ……………………………......319
37. Теория поля …………………………………………….. ….335
38. Оператор Гамильтона ……………………………………..347
39. Функция комплексного переменного……………………. 350
40. Дифференцирование функций комплексного
переменного, условия Коши- Римана …………………..….....362
41. Интегрирование функций комплексного переменного …364
42. Ряд Лорана………………………………...………………. ..366
43. Преобразование Лапласа ………………………………….379
44. Задача Коши для обыкновенных линейных
дифференциальных уравнений ……………………………......385
Заключение……………………….……………….……….........388
Библиографический список ……...………………...…….........389
Учебное издание
Катрахова Алла Анатольевна
Купцов Валерий Семенович
Купцова Екатерина Валериевна
КУРС ЛЕКЦИЙ
ПО ДИСЦИПЛИНЕ «МАТЕМАТИКА»
В авторской редакции
Подписано к изданию 13.05. 2015.
Объем данных 6,17 Mб
ФГБОУ ВПО «Воронежский государственный
технический университет»
394026 Воронеж, Московский просп.,14
Дата: 2016-10-02, просмотров: 208.
