Рассмотрим систему дифференциальных уравнений вида
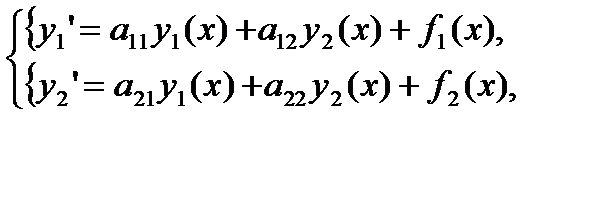 (28.1)
(28.1)
где f1(x) и f2(x)-непрерывные функции. Система (28.1) называется однородной, если f1(x)=0, f2(x)=0, 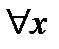 . Решением системы (28.1) называется вектор-функция
. Решением системы (28.1) называется вектор-функция
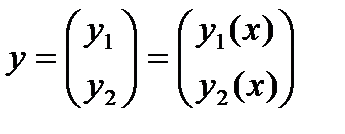 , (28.2)
, (28.2)
координатные функции которой для всех х удовлетворяют
каждому из равенств (28.1).
Задача Коши для системы (28.1) формируется следующим образом: найти решение y=y(x) системы, которые при х=х0 удовлетворяют условиям y1(x0)=y10, y2(x0)=y20, где y10 и y20-заданные числа.
Если ввести векторы у, f(x)= 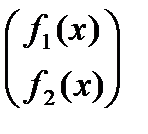 и матрицу
и матрицу
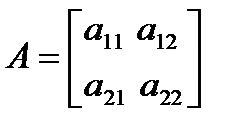 , то систему можно записать в матричном виде
, то систему можно записать в матричном виде
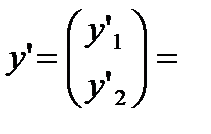
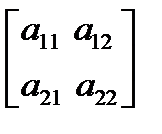
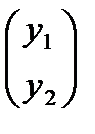 =Ay+f(x). (28.3)
=Ay+f(x). (28.3)
Вектор-функция 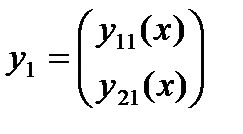 и
и 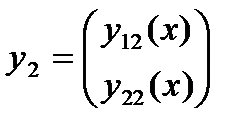 называются линейно независимыми, если существуют числа
называются линейно независимыми, если существуют числа 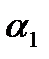 и
и 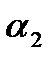 , такие что
, такие что
 (28.4)
(28.4)
и линейно независимыми, если тождество (28.4) выполняется в единственном случае, когда 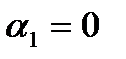 и
и 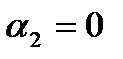 . Фундаментальной системой решений однородной системы
. Фундаментальной системой решений однородной системы 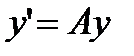 называется два ее линейно независимых решения
называется два ее линейно независимых решения 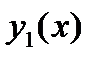 ,
, 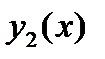 . Общим решением системы
. Общим решением системы  называется решение
называется решение
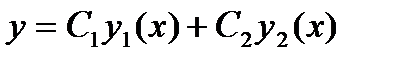 , (28.5)
, (28.5)
где С1 и С2 – произвольные постоянные, у1, у 2 – фундаментальная система решений. Частным решением у0 системы (28.1) называется любое решение, удовлетворяющее ей. Общим решением неоднородной системы является вектор-функция
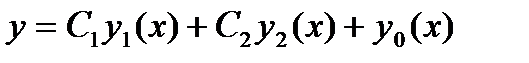 , (28.6)
, (28.6)
где 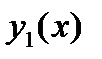 ,
, 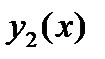 - фундаментальная система,
- фундаментальная система, 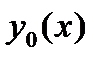 - некоторое частное решение. Рассмотрим метод исключения
- некоторое частное решение. Рассмотрим метод исключения
Пример . Методом исключения решить задачу Коши:
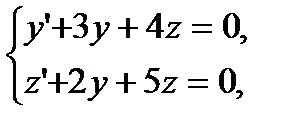
где 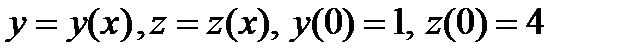 .
.
Решение: Продифференцируем первое уравнение системы: 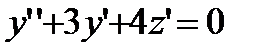 и подставим в него
и подставим в него 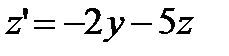 из второго уравнения. Тогда получим
из второго уравнения. Тогда получим 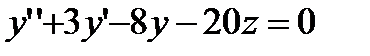 . В это уравнение подставим
. В это уравнение подставим 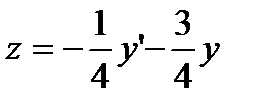 из первого уравнения, получим
из первого уравнения, получим 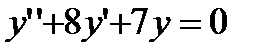 . Решив характеристическое уравнение
. Решив характеристическое уравнение 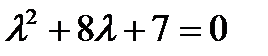 , найдем
, найдем 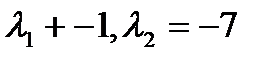 и общее решение
и общее решение 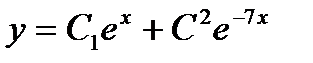 . Тогда
. Тогда
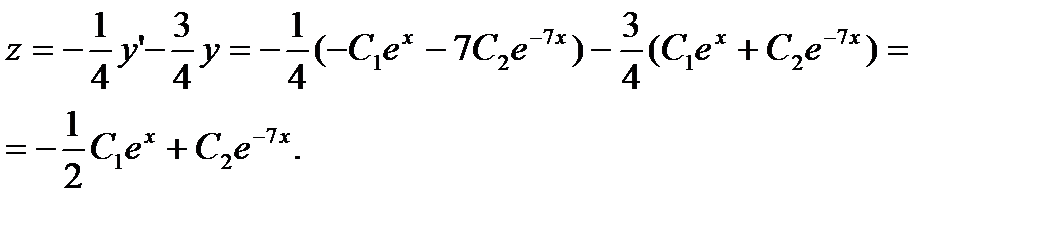
Используя начальные условия, получим
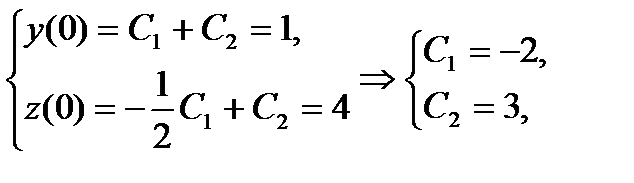
т.е. решением задачи Коши являются функции
 .
.
ЧИСлоВЫЕ ряды
Основные понятия и определения числовых рядов
Числовым рядом называется сумма бесконечного множества слагаемых
a1+a2+a3+...= 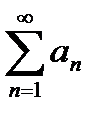 , (29.1)
, (29.1)
являющихся членами бесконечной числовой последовательности 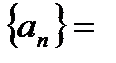 a1,a2,a3,…,an , ... Член an=ƒ(n) называется общим членом ряда (29.1). Сумма первых n членов ряда
a1,a2,a3,…,an , ... Член an=ƒ(n) называется общим членом ряда (29.1). Сумма первых n членов ряда
Sn=a1+a2+...+an называется n-ой частичной суммой Sn.
Ряд (29.1) называется сходящимся, если предел последовательности его частичных сумм {Sn} при неограниченном возрастании n стремится к конечному пределу: 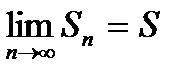 . Тогда величина S называется суммой ряда, а величина
. Тогда величина S называется суммой ряда, а величина
R=S-Sn=an+1+an+2+an+3+... – остаток ряда (29.1).
Если предел 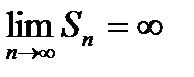 или
или  или
или 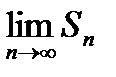 не существует, то ряд (29.1) называется расходящимся.
не существует, то ряд (29.1) называется расходящимся.
Расходящийся ряд суммы не имеет. Сходимость или
расходимость ряда не нарушается, если прибавить или отбросить конечное число его членов. Например, ряд
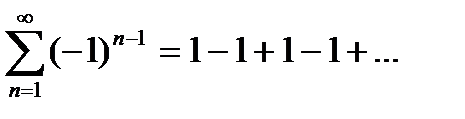 расходящийся, так как последовательность частичных сумм {Sn} не имеет предела:
расходящийся, так как последовательность частичных сумм {Sn} не имеет предела:
S1=1; S2=1-1=0; S3=1-1+1=1; … .
Если ряд (29.1) сходится, то его общий член an стремится к
нулю при n→∞, то есть 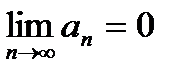 - необходимый признак сходимости любого ряда. Обратное утверждение неверно. Значит, если
- необходимый признак сходимости любого ряда. Обратное утверждение неверно. Значит, если
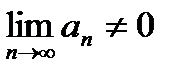 , то ряд (29.1) расходится.
, то ряд (29.1) расходится.
Нахождение суммы знакоположительного ряда
Пусть дан ряд 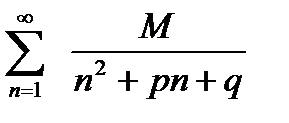 , где M, p, q — целые числа. Если корни знаменателя в общем члене
, где M, p, q — целые числа. Если корни знаменателя в общем члене 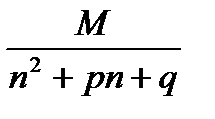 различаются на целое число, то члены последовательности {Sn} частичных сумм такого ряда нетрудно найти, ибо в выражении
различаются на целое число, то члены последовательности {Sn} частичных сумм такого ряда нетрудно найти, ибо в выражении
Sn=a1+a2+...+an многие слагаемые взаимно уничтожаются. Поэтому, найдя корни квадратного трехчлена n2+np+q, разлагаем на множители знаменатель дроби, затем разлагаем общий член an ряда на элементарные дроби и выписываем несколько членов ряда, чтобы увидеть закономерность, какие слагаемые сократятся при вычислении n-ой частичной суммы. Составляем Sn и вычисляем сумму ряда по формуле 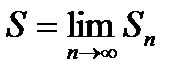 .
.
Пример 1.Найти сумму следующих рядов:
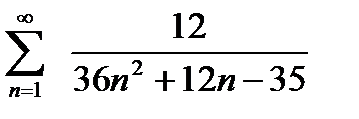
Решение.
а) Находим корни уравнения 36n²+12n-35=0.
Дискриминант D=144×36>0; корни n1=5/6,n2=-7/6, различаются на целое число 2. Тогда 36n²+12n-35=36(n-5/6)(n+7/6).
б) Общий член ряда разлагаем на элементарные дроби методом неопределенных коэффициентов:
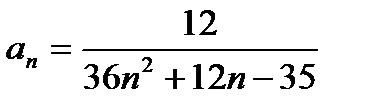 =
= 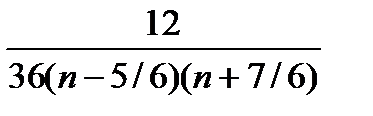 =
=
= 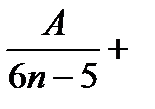
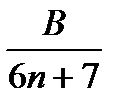 , где А, В — коэффициенты, подлежащие определению. Умножив на знаменатель левой части, получаем тождество 12=A(6n+7)+B(6n-5). Полагая последовательно n2=-7/6 и n1=5/6, находим: при n2=-7/6: 12=-12B; B=-1;
, где А, В — коэффициенты, подлежащие определению. Умножив на знаменатель левой части, получаем тождество 12=A(6n+7)+B(6n-5). Полагая последовательно n2=-7/6 и n1=5/6, находим: при n2=-7/6: 12=-12B; B=-1;
при n1=5/6: 12=12A; A=1. Значит, an= 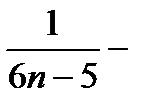
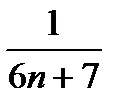 .
.
в) Выписываем, начиная с n=2, несколько членов ряда, чтобы увидеть, какие слагаемые сокращаются при вычислении
Sn: a2= 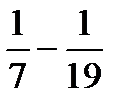 , a3=
, a3= 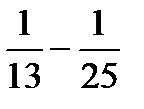 , a4=
, a4= 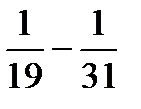 ,
,
a5= 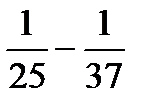 , a6=
, a6= 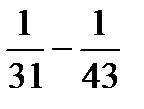 ,…, an-2=
,…, an-2= 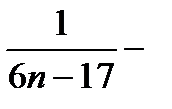
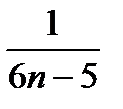 ,
,
an-1= 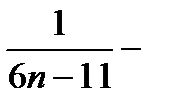
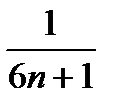 , an=
, an= 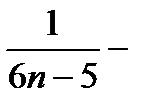
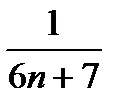 .
.
г) Составляем n-ую частичную сумму ряда и сокращаем все слагаемые, какие возможно:
Sn= 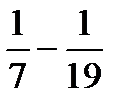 +
+ 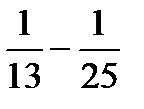 +
+ 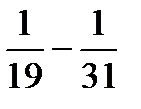 +
+ 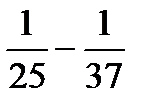 +
+ 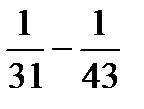 +…
+…
+ 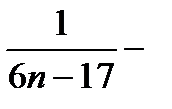
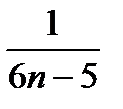 +
+ 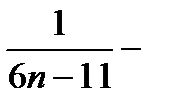
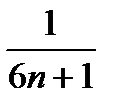 +
+ 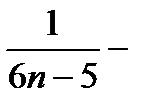
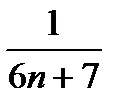 =
= 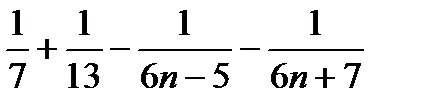 ..
..
д) Вычисляем сумму ряда
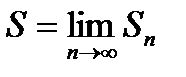 ,
, 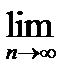
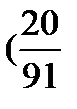 -
- 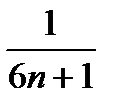 -
- 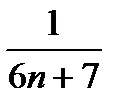 )=
)= 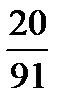
Исследование сходимости знакоположительных рядов
Рассмотрим ряд с положительными членами
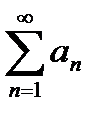 =a1+a2+a3+ , (29.2)
=a1+a2+a3+ , (29.2)
где 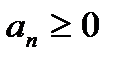 , при
, при 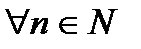 .
.
Так как все члены ряда (29.2) положительны, то частичная сумма Sn возрастает с возрастанием n. Поэтому знакоположительный ряд (29.2) либо сходится, когда 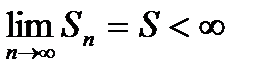 , либо его сумма бесконечная:
, либо его сумма бесконечная: 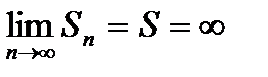 и ряд расходится.
и ряд расходится.
Перечислим основные достаточные признаки сходимости и расходимости знакоположительных рядов.
I. Первый признак сравнения. Если  0
0 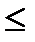 an
an  bn, начиная с
bn, начиная с
некоторого номера n=n0, и ряд
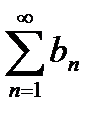 =b1+b2+b3+… (29.3)
=b1+b2+b3+… (29.3)
сходится, то ряд (29.2) также сходится. Если ряд (29.2) расходится, то расходится и ряд (29.3).
II. Второй (предельный) признак сравнения. Если существует конечный и отличный от нуля предел 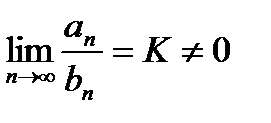 (в частности, если an~bn), то ряды (29.2) и (29.3) сходятся или расходятся одновременно.
(в частности, если an~bn), то ряды (29.2) и (29.3) сходятся или расходятся одновременно.
В качестве рядов для сравнения удобно использовать один из следующих рядов:
1. Геометрический ряд
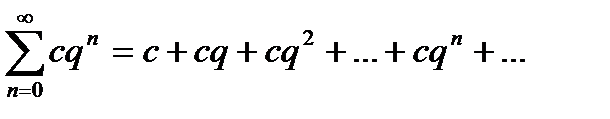
(c=const), который сходится при 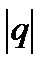 <1 и расходится при
<1 и расходится при 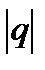
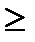 1.
1.
2. Гармонический ряд 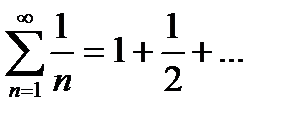 , являющийся расходящимся рядом.
, являющийся расходящимся рядом.
3. Обобщенный гармонический ряд (Дирихле)
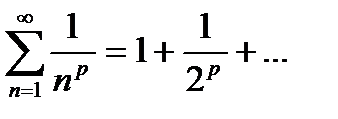 , который сходится при p>1 и расходится при p
, который сходится при p>1 и расходится при p 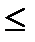 1.
1.
Замечание. Для оценки общего члена ряда удобно использовать неравенства -1 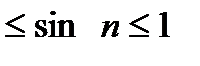 , -1
, -1 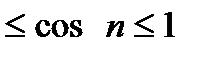 ,
,
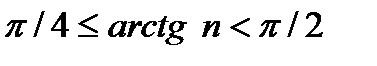 ,
, 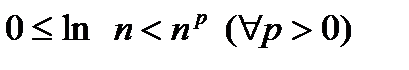 , и т. п.
, и т. п.
Пример 2. Ряд
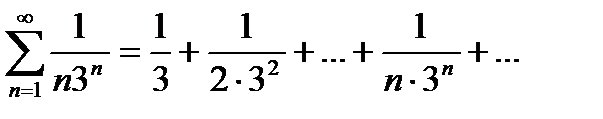
сходится по первому признаку сравнения, так как
an= 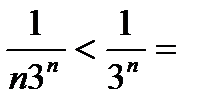 bn Для сравнения взяли сходящийся геометрический ряд
bn Для сравнения взяли сходящийся геометрический ряд 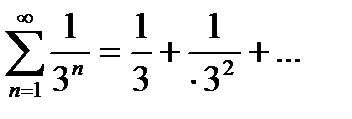 , составленный из членов бесконечно убывающей геометрической прогрессии
, составленный из членов бесконечно убывающей геометрической прогрессии
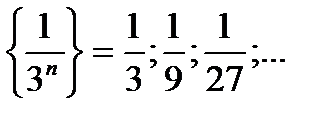 , знаменатель которой q=1/3 меньше 1, а сумма всех ее членов равна
, знаменатель которой q=1/3 меньше 1, а сумма всех ее членов равна .
III. Признак Даламбера. Пусть an>0(начиная с
некоторого номера n=n0). Если для ряда (29.2) существует
предел отношения последующего члена an+1к предыдущему an, т. е. 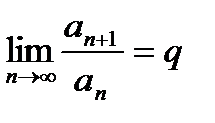 , то при q<1 ряд (29.2) сходится, а при q>1 ряд (29.2) расходится.
, то при q<1 ряд (29.2) сходится, а при q>1 ряд (29.2) расходится.
IV. Признак Коши. Пусть an 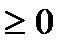 (начиная с некоторого номера n=n0). Если для ряда (29.2) существует предел
(начиная с некоторого номера n=n0). Если для ряда (29.2) существует предел
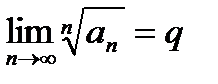 , то при q<1 ряд (29.2) сходится, а при q>1 ряд (29.2) расходится.
, то при q<1 ряд (29.2) сходится, а при q>1 ряд (29.2) расходится.
Замечание 1. Признаки Даламбера и Коши при q=1 ответа не дают. Тогда следует применить другой признак сходимости.
Замечание 2. При вычислении пределов полезно иметь в виду, что 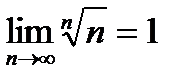 ,
, 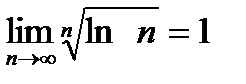 ,
, 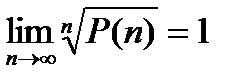 , где P(n) —многочлен относительно n. Например,
, где P(n) —многочлен относительно n. Например, 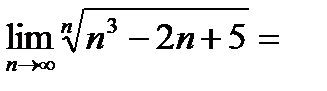
= 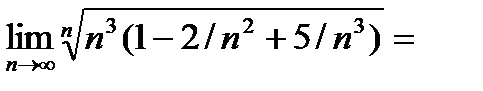
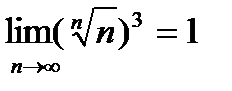 .
.
V. Интегральный признак Коши. Если an=f(n),
где функция f(x) положительна, монотонно убывает и непрерывна при 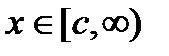 , где
, где 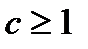 , то ряд
, то ряд сходится или расходится в зависимости от того, сходится или расходится несобственный интеграл
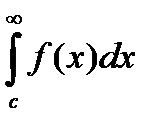 . Устанавливают сходимость несобственного интеграла обычно по определению:
. Устанавливают сходимость несобственного интеграла обычно по определению: 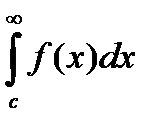 =
= 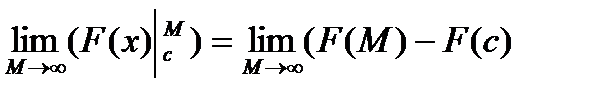 , когда первообразная функции F(x) легко вычисляется.
, когда первообразная функции F(x) легко вычисляется.
.
Пример 3. Ряд 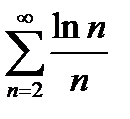 расходящийся по интегральному признаку. Действительно, an=f(n)=
расходящийся по интегральному признаку. Действительно, an=f(n)= 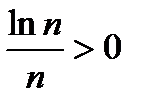 при n>2функция f(x)=
при n>2функция f(x)= 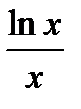 -положительная, непрерывнаяи монотонно убывающаяпри
-положительная, непрерывнаяи монотонно убывающаяпри 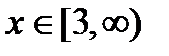 ,ибо
,ибо 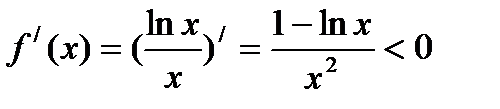 ,т.к.
,т.к. 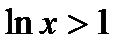 при
при 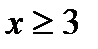 ,
, 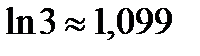 и интеграл
и интеграл 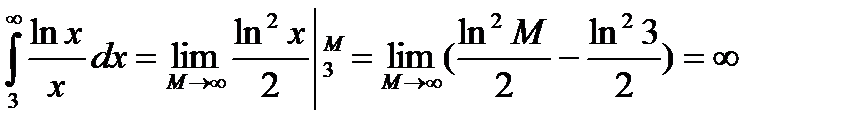 , то есть расходится. Здесь
, то есть расходится. Здесь 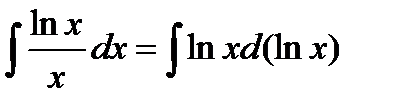
Знакопеременные ряды. Признак Лейбница
для знакочередующихся рядов
Рассмотрим ряд, члены которого имеют разные знаки:
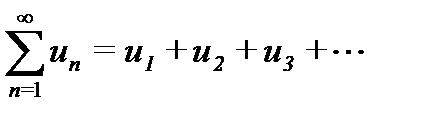 (29.4)
(29.4)
Ряды с произвольным чередованием знаков всех членов называются знакопеременными рядами. Ряд вида
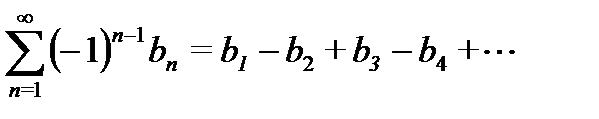 , (29.5)
, (29.5)
где величины 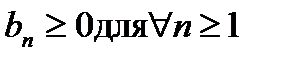 , называется знакочередующимся. Это такой ряд, в котором два любых соседних члена имеют противоположные знаки.
, называется знакочередующимся. Это такой ряд, в котором два любых соседних члена имеют противоположные знаки.
Признаки сходимости знакопеременных рядов.
Если ряд
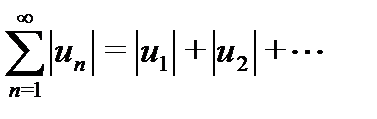 , (29.6)
, (29.6)
составленный из модулей (абсолютных величин) членов ряда
(29.4) сходится, то ряд (29.4) так же сходится и называется абсолютно сходящимся. Для исследования на абсолютную сходимость ряда (29.4) можно исследовать для ряда (29.6) известные признаки сходимости для знакоположительных рядов. В частности:
а) Ряд (29.4) сходится абсолютно, если абсолютные величины членов ряда (29.4) не превосходят членов сходящегося знакоположительного ряда: 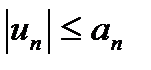 , где ряд
, где ряд сходящийся.
б) Ряд (29.4) сходится абсолютно, если 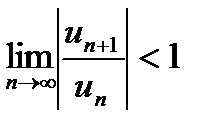 или
или 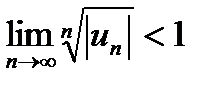 .
.
в) Если 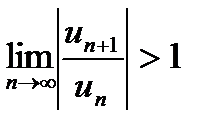 или
или 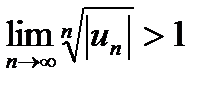 , то расходится не только ряд (29.6), составленный из модулей, но и исходный ряд
, то расходится не только ряд (29.6), составленный из модулей, но и исходный ряд
(29.4). В общем случае из расходимости ряда из модулей (29.6) не следует расходимость ряда (29.4). Ряд (29.4) называется условно (не абсолютно) сходящимся, если он сходится, а соответствующий ему ряд (29.6) из модулей расходится.
Пример 4 .
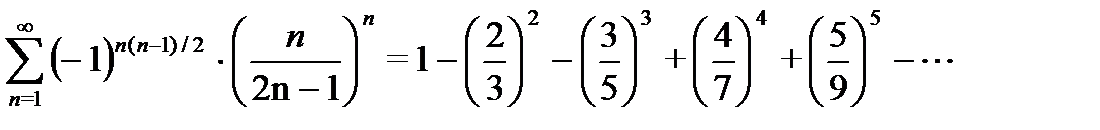 .
.
Решение. Составим ряд из абсолютных величин членов данного ряда
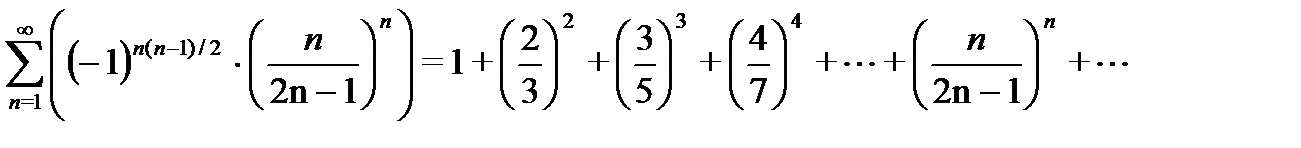 Так как
Так как 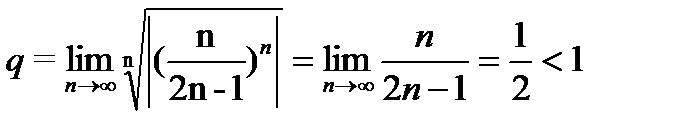 , то исследуемый ряд сходится абсолютно.
, то исследуемый ряд сходится абсолютно.
Признак Лейбница. Если для знакочередующегося ряда (29.5) выполнены два условия: 1) его члены убывают по абсолютной величине 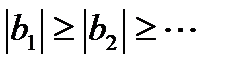 и 2) его общий член стремится к нулю при
и 2) его общий член стремится к нулю при 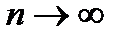 , то ряд (29.5) сходится ( по крайней мере, условно). Для остатка ряда Rn = S-Sn, в этом случае имеет место оценка
, то ряд (29.5) сходится ( по крайней мере, условно). Для остатка ряда Rn = S-Sn, в этом случае имеет место оценка 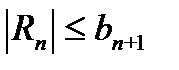 , то есть остаток ряда Rn не превосходящей первого из отброшенных его членов.
, то есть остаток ряда Rn не превосходящей первого из отброшенных его членов.
Пример 5.Исследовать на сходимость ряд. 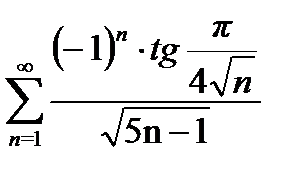 ,
,
Решение. 1) Данный знакочередующийся ряд
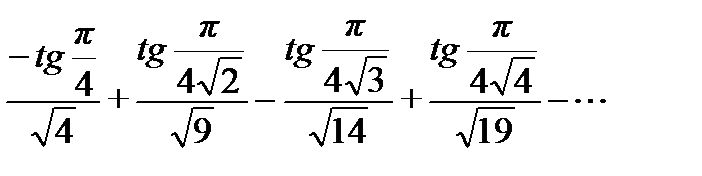 сходится по признаку Лейбница, так как выполнены два условия: монотонное убывание модулей членов ряда
сходится по признаку Лейбница, так как выполнены два условия: монотонное убывание модулей членов ряда 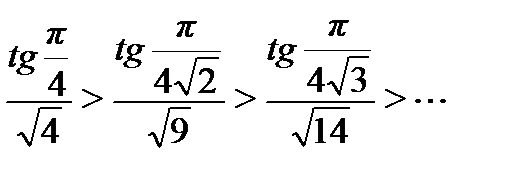 ;
;
2) 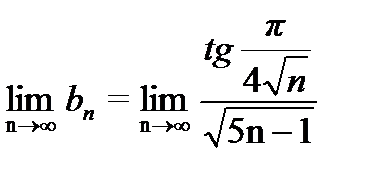 =.
=. 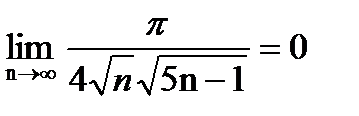
Сходимость данного ряда условная, так как ряд из модулей его членов 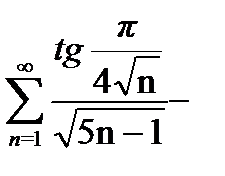 расходится вместе с рядом
расходится вместе с рядом 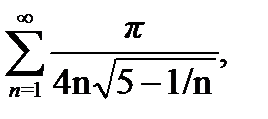 который получили при упрощении общего члена, воспользовавшись тем, что
который получили при упрощении общего члена, воспользовавшись тем, что 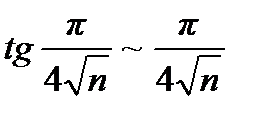 при
при  .
.
Ответ: Исследуемый ряд условно сходится.
Отметим следующие свойства сходящихся
знакопеременных рядов
Свойство 1. Если ряд (29.4) абсолютно сходится, то ряд,
полученный после любой перестановки бесконечного
множества его членов, абсолютно сходится и имеет ту же сумму, что и первоначальный ряд.
Свойство 2. Если ряд (29.4) условно сходится, то от перемены мест его членов сумма ряда изменяется и больше того имеет место теорема (Римана): Сумма ряда, сходящегося условно зависит от порядка, в котором расположены его члены. Изменяя этот порядок, можно заставить ряд иметь своей суммой любое число или сделать его даже расходящимся.
Приближенное вычисление суммы
знакочередующегося ряда
Дан ряд 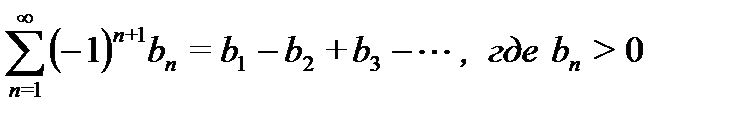 . (29.7)
. (29.7)
Требуется с заданной точностью 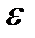 вычислить его сумму
вычислить его сумму
( в случае сходимости ряда). Если выполнены два условия признака Лейбница:
1) 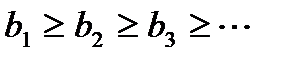 и 2)
и 2) 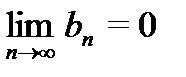 , то для остатка Rn ряда (29.7) справедливо неравенство
, то для остатка Rn ряда (29.7) справедливо неравенство 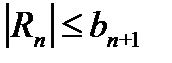 , где
, где 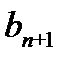 - первый из отброшенных членов ряда. Если
- первый из отброшенных членов ряда. Если 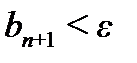 , то и подавно
, то и подавно 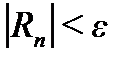 . Поэтому, решая неравенство
. Поэтому, решая неравенство 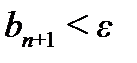 при конкретных значениях n, находим число n - количество членов ряда, которое необходимо взять для вычисления суммы S. Затем непосредственно вычисляем n-ую частичную сумму Sn . Так как
при конкретных значениях n, находим число n - количество членов ряда, которое необходимо взять для вычисления суммы S. Затем непосредственно вычисляем n-ую частичную сумму Sn . Так как 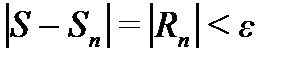 , то приближенно за сумму S ряда принимаем n-ую частичную суммы Sn:
, то приближенно за сумму S ряда принимаем n-ую частичную суммы Sn:
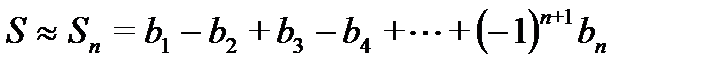 .
.
Пример 6 .Вычислить сумму ряда с точностью έ.
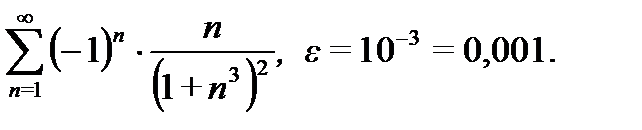
Решение.Данный ряд знакочередующийся и сходящийся абсолютно, так как 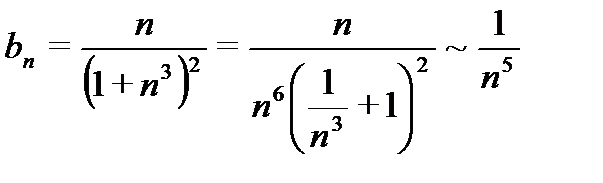
и ряд Дирихле сходится (p=5>1).
Члены ряда монотонно убывают по абсолютной величине.
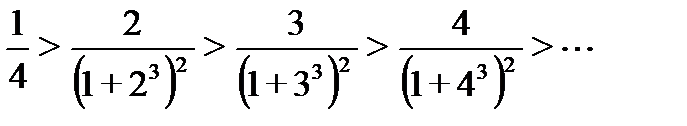
Следовательно, справедливо неравенство
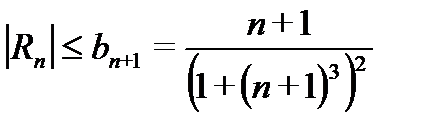 . По условию έ =0.001.
. По условию έ =0.001.
Если 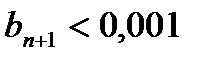 , то и
, то и 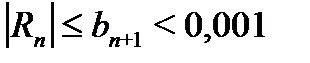 . Поэтому, решая неравенство
. Поэтому, решая неравенство 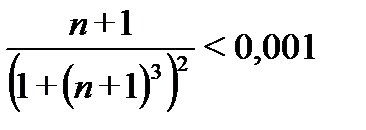 , находим при
, находим при
n=1: b1=2/81 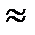 0,0247>0,001
0,0247>0,001
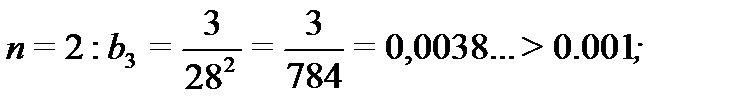
n=3: b3=4/652 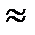 0,00094<0,001.
0,00094<0,001.
Итак, 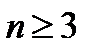 . Получили, что четвертый член удовлетворяет заданной точности
. Получили, что четвертый член удовлетворяет заданной точности 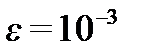 . Значит, для вычисления суммы ряда с точностью 0.001 достаточно взять первые три члена ряда. Вычисляем частичную сумму
. Значит, для вычисления суммы ряда с точностью 0.001 достаточно взять первые три члена ряда. Вычисляем частичную сумму 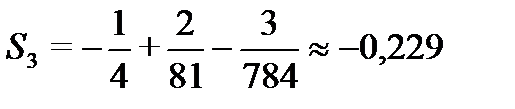 . Таким образом, сумма, вычисленная с заданной точностью, данного ряда
. Таким образом, сумма, вычисленная с заданной точностью, данного ряда 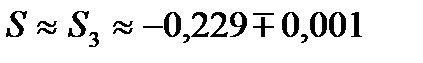 .
.
Ответ: 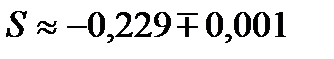 .
.
Функциональные ряды
Основные теоретические сведения
Ряд
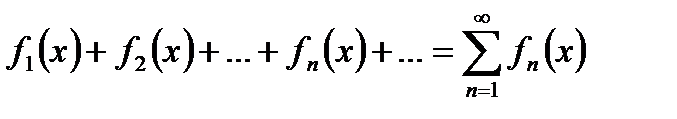 , (30.1)
, (30.1)
члены которого – функции от х, называется функциональным.
Множество значений аргумента х, при которых функции
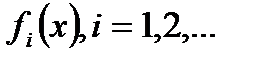 определены и функциональный ряд (30.1) сходится, называется областью сходимости этого ряда. При действительном значении аргумента областью сходимости является какой-либо промежуток оси ОХ. При конкретном значении
определены и функциональный ряд (30.1) сходится, называется областью сходимости этого ряда. При действительном значении аргумента областью сходимости является какой-либо промежуток оси ОХ. При конкретном значении 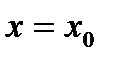 ряд (30.1) становится числовым. Функция
ряд (30.1) становится числовым. Функция 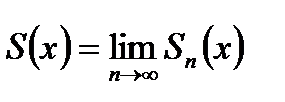 , где
, где 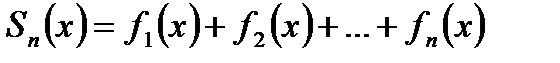 - сумма первых n членов ряда (30.1), а х принадлежит области сходимости, называется суммой ряда. Разность между суммой S(x) сходящегося ряда и его частичной суммой
- сумма первых n членов ряда (30.1), а х принадлежит области сходимости, называется суммой ряда. Разность между суммой S(x) сходящегося ряда и его частичной суммой 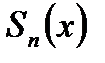 называется остатком ряда (30.1):
называется остатком ряда (30.1):
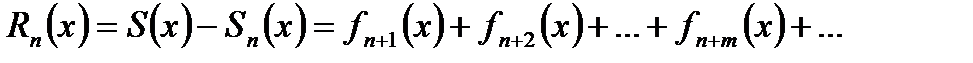 ,
,
причем в области сходимости ряда 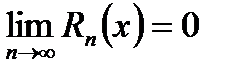 .
.
Сходящийся функциональный ряд (30.1) называется равномерно сходящимся в некоторой области Х, если для любого сколь угодно малого числа ε >0 найдется такое целое число N >0, начиная с которого, т.е. при n  N, выполняется неравенство
N, выполняется неравенство 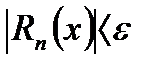 одновременно сразу для всех х из области Х. Достаточным признаком равномерной сходимости рядов является следующий признак Вейерштрасса. Ряд (30.1 равномерно сходится в данной области Х, если существует такой сходящийся числовой ряд
одновременно сразу для всех х из области Х. Достаточным признаком равномерной сходимости рядов является следующий признак Вейерштрасса. Ряд (30.1 равномерно сходится в данной области Х, если существует такой сходящийся числовой ряд 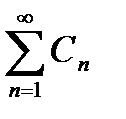 , что для всех значений х
, что для всех значений х 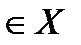 имеет место неравенство
имеет место неравенство 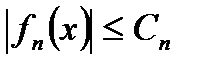 . При этом сходящийся числовой ряд
. При этом сходящийся числовой ряд 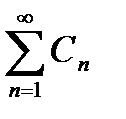
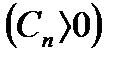 называется мажорантой для ряда (30.1).
называется мажорантой для ряда (30.1).
Пример 1.Ряды  являются равномерно сходящимися в любой области, если ряд
являются равномерно сходящимися в любой области, если ряд 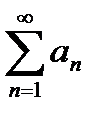 абсолютно сходится, т.к.
абсолютно сходится, т.к. 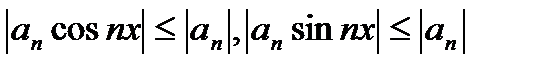 , а ряд
, а ряд 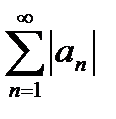 сходится.
сходится.
Свойства равномерно сходящихся рядов:
1. Если члены равномерно сходящегося ряда (30.1) непрерывны на некотором отрезке, то его сумма также непрерывна на этом отрезке.
2. Равномерно сходящийся ряд (30.1) можно почленно интегрировать в данной области Х, если его члены непрерывны в области Х, причем сумма интегралов от членов ряда равна интегралу от суммы данного ряда:
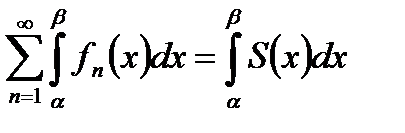 , где
, где 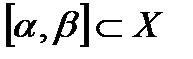
3. Если ряд (30.1) сходится к сумме S(x) на отрезке Х, причем его члены имеют непрерывные производные 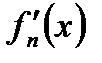 при х
при х 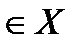 и ряд, составленный из производных
и ряд, составленный из производных 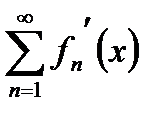 , равномерно сходящийся на том же отрезке, то
, равномерно сходящийся на том же отрезке, то 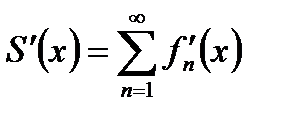 , т.е. ряд (30.1) можно почленно дифференцировать.
, т.е. ряд (30.1) можно почленно дифференцировать.
Нахождение области сходимости
функциональных рядов
Для определения области сходимости функционального
ряда (30.1) достаточно применить к этому ряду известные признаки сходимости, считая аргумент х фиксированным. Например, при использовании признаков Даламбера или Коши поступают так:
1) Находят q(x) по одной из формул (если пределы
существуют)
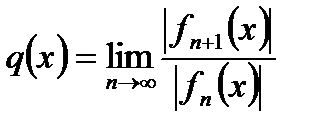 или
или 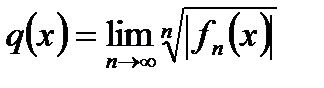 (30.2)
(30.2)
2) Решают неравенство q(x)<1 (т.к. по признакам
Даламбера и Коши ряд сходится при q<1 и расходится при q>1). В результате находим интервал сходимости.
3) Исследуется поведение ряда в концевых точках
интервала сходимости.
Пример2. Найти область сходимости ряда 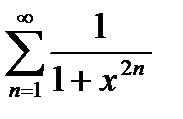
Решение. Рассмотрим три случая
a) Если 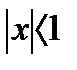 , то
, то 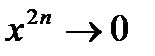 при
при 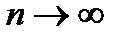 и
и
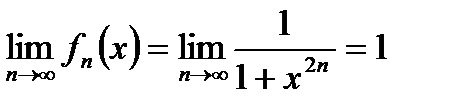 . Необходимый признак сходимости ряда не выполнен. Следовательно, ряд расходится при -1<x<1.
. Необходимый признак сходимости ряда не выполнен. Следовательно, ряд расходится при -1<x<1.
b) Если 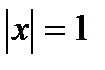 , то также получаем расходящийся ряд
, то также получаем расходящийся ряд
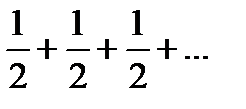
c) Если 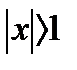 , то применим первый признак сравнения
, то применим первый признак сравнения
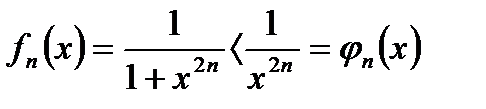 , где сходящийся
, где сходящийся
ряд 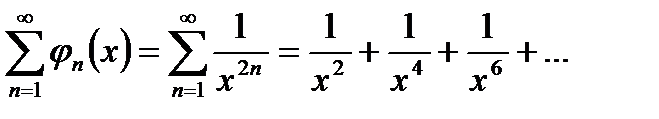 представляет
представляет
собой сумму бесконечно убывающей геометрической
прогрессии со знаменателем 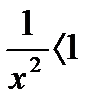 , т.е.
, т.е. 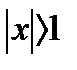 . Итак, исследуемый ряд сходится при
. Итак, исследуемый ряд сходится при 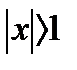 ; его область сходимости
; его область сходимости 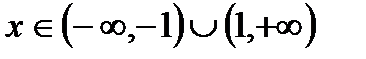
Интервал и радиус сходимости степенного ряда
Степенным рядом называется функциональный ряд вида
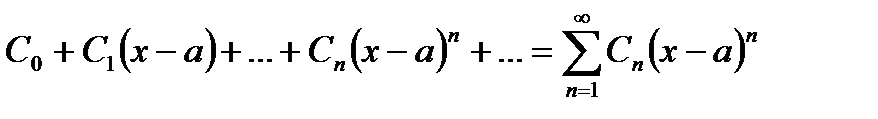 , (30.3)
, (30.3)
где коэффициенты 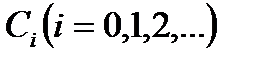 - действительные числа.
- действительные числа.
Основное свойство степенных рядов состоит в том, что если ряд (30.3) сходится при 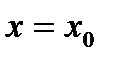 , то он сходится ( и притом абсолютно) при всяком значении х, удовлетворяющем неравенству
, то он сходится ( и притом абсолютно) при всяком значении х, удовлетворяющем неравенству 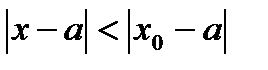 (теорема Абеля). Следствием теоремы Абеля является существование для всякого степенного ряда (30.3) интервала сходимости
(теорема Абеля). Следствием теоремы Абеля является существование для всякого степенного ряда (30.3) интервала сходимости 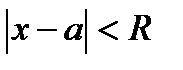 с центром в точке х=а, внутри которого ряд (30.3) сходится абсолютно ; при
с центром в точке х=а, внутри которого ряд (30.3) сходится абсолютно ; при 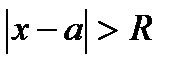 ряд (30.3) расходится. Радиус сходимости R (т.е. половина длины интервала сходимости) может быть в частных случаях равен также 0 и ∞. В конечных точках
ряд (30.3) расходится. Радиус сходимости R (т.е. половина длины интервала сходимости) может быть в частных случаях равен также 0 и ∞. В конечных точках 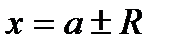 интервала сходимости возможна как сходимость, так и расходимость ряда (30.3). Интервал сходимости определяют обычно с помощью признаков Даламбера или Коши, применяя их к ряду, составленному из абсолютных величин членов исходного ряда. Но если
интервала сходимости возможна как сходимость, так и расходимость ряда (30.3). Интервал сходимости определяют обычно с помощью признаков Даламбера или Коши, применяя их к ряду, составленному из абсолютных величин членов исходного ряда. Но если
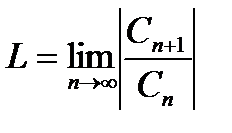 или
или 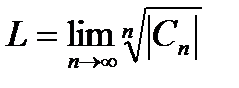 , (30.4)
, (30.4)
где 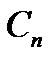 и
и 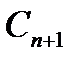 - коэффициенты соответственно n-го и (n+1)-го членов ряда (30.3), то радиус сходимости ряда (30.3) определяется по формуле
- коэффициенты соответственно n-го и (n+1)-го членов ряда (30.3), то радиус сходимости ряда (30.3) определяется по формуле 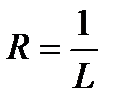 . Однако пользоваться формулами (30.4) следует весьма осторожно. Если L=0, то R=∞ и ряд (30.3) сходится при
. Однако пользоваться формулами (30.4) следует весьма осторожно. Если L=0, то R=∞ и ряд (30.3) сходится при 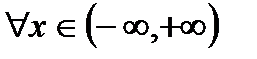 . Если L=∞, то R=0 и ряд (30.3) расходится при любом х, кроме х=0.
. Если L=∞, то R=0 и ряд (30.3) расходится при любом х, кроме х=0.
Пример 3 .Найти радиус и интервал сходимости
степенного ряда 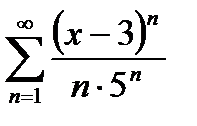
Решение.Имеем коэффициенты ряда 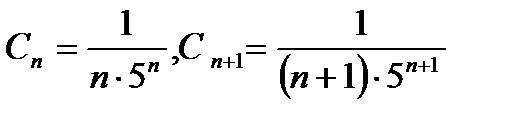 . Найдем число L (см.формулы 30.4).
. Найдем число L (см.формулы 30.4). 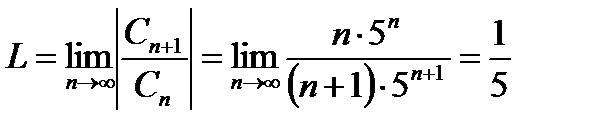 . Следовательно, радиус сходимости R=5. Интервал сходимости ряда
. Следовательно, радиус сходимости R=5. Интервал сходимости ряда 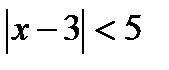 с центром в точке
с центром в точке 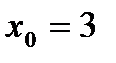 или
или 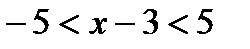 есть
есть 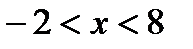 . Исследуем поведение ряда в концевых точках интервала:
. Исследуем поведение ряда в концевых точках интервала:
При х=8: 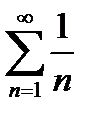 - расходящийся гармонический ряд
- расходящийся гармонический ряд
При х=-2: 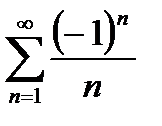 - условно сходящийся (по Лейбницу).
- условно сходящийся (по Лейбницу).
Ответ: R=5; 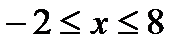 .
.
Нахождение суммы функционального ряда
Рассмотрим некоторые приемы нахождения суммы
функционального ряда и области его сходимости к этой сумме.
Нахождение суммы ряда почленным интегрированием.
I. Пусть дан ряд вида 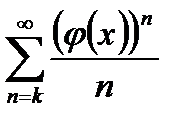 . По признаку Коши или
. По признаку Коши или
признаку Даламбера область сходимости определяется неравенством 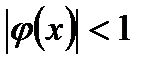 . Если
. Если  , то ряд
, то ряд 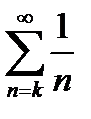 - расходящийся.
- расходящийся.
Если 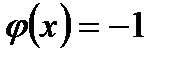 , то ряд
, то ряд 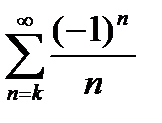 сходится условно (по признаку Лейбница). Следовательно, область сходимости находится из неравенства
сходится условно (по признаку Лейбница). Следовательно, область сходимости находится из неравенства 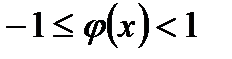 . Затем делаем замену
. Затем делаем замену 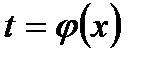 в исходном ряде; получаем степенной ряд
в исходном ряде; получаем степенной ряд 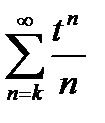 с областью сходимости
с областью сходимости 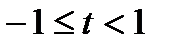 . Используем формулу для вычисления суммы членов бесконечно убывающей геометрической прогрессии со знаменателем
. Используем формулу для вычисления суммы членов бесконечно убывающей геометрической прогрессии со знаменателем 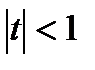
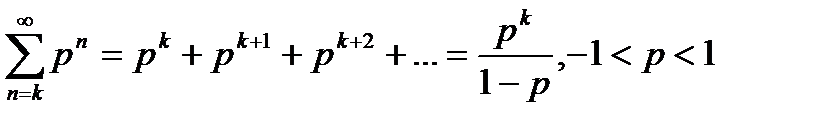 (30.5)
(30.5)
и очевидное равенство
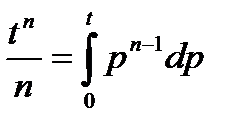 (30.6)
(30.6)
Учитывая, что степенной ряд можно почленно интегрировать по любому отрезку 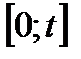 , целиком принадлежащему интервалу сходимости, и используя формулу (30.6), получаем
, целиком принадлежащему интервалу сходимости, и используя формулу (30.6), получаем
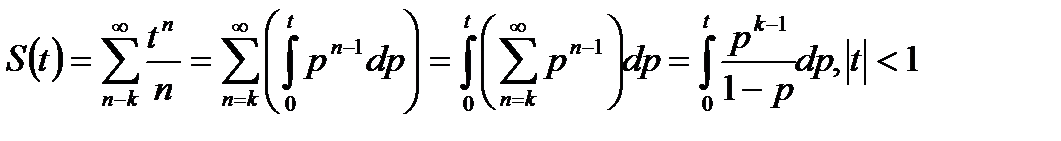 Заметим, что так как ряд (30.5) сходится в граничной точке
Заметим, что так как ряд (30.5) сходится в граничной точке
t=-1, то сумма ряда непрерывна в этой точке (справа) и 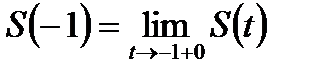 . Далее вычисляем интеграл (с переменным верхним пределом), заменяем t на
. Далее вычисляем интеграл (с переменным верхним пределом), заменяем t на 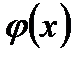 и получаем ответ.
и получаем ответ.
II. Если дан ряд вида 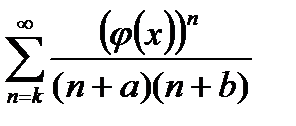 , то следует либо
, то следует либо
применить теорему о почленном интегрировании степенного ряда дважды, либо разложить дробь на элементарные 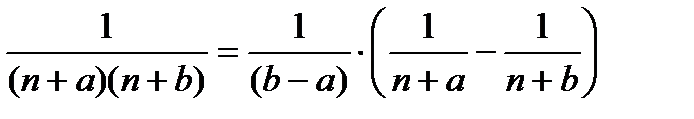 и вычислить сумму каждого ряда почленным интегрированием.
и вычислить сумму каждого ряда почленным интегрированием.
Пример 4. Найти сумму ряда 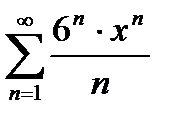 и указать область
и указать область
его сходимости к этой сумме.
Решение. Данный ряд степенной. Находим его интервал сходимости. По признаку Коши имеем
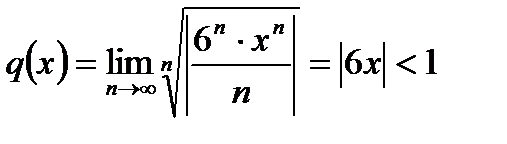 . Из неравенства находим
. Из неравенства находим 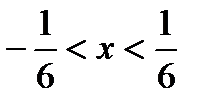 . Исследуем поведение ряда в граничных точках. При
. Исследуем поведение ряда в граничных точках. При 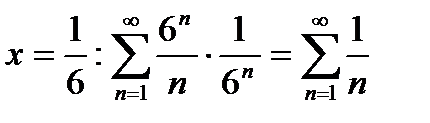 - расходящийся гармонический ряд. При
- расходящийся гармонический ряд. При 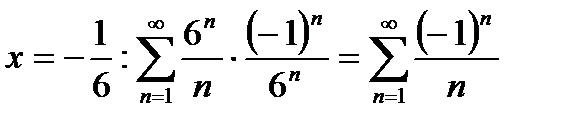 - условно сходящийся ряд по признаку Лейбница. Следовательно, данный ряд сходится при
- условно сходящийся ряд по признаку Лейбница. Следовательно, данный ряд сходится при 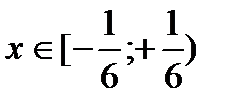 . Для нахождения суммы ряда сделаем замену
. Для нахождения суммы ряда сделаем замену 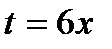 . Получим геометрический ряд
. Получим геометрический ряд 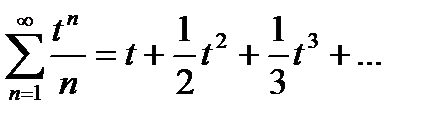 , сходящийся при
, сходящийся при 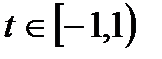 . Используя равенство (30.6) и почленное интегрирование степенного ряда, получаем:
. Используя равенство (30.6) и почленное интегрирование степенного ряда, получаем:
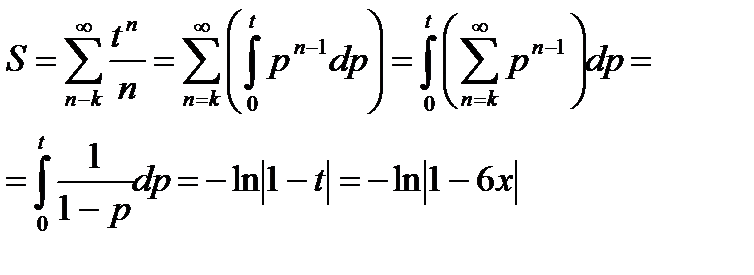
Ответ: 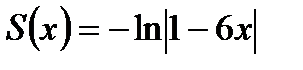 для
для 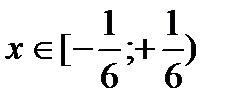 .
.
Замечание. Степенной ряд (30.3) сходится абсолютно и равномерно на всяком отрезке, лежащем внутри его интервала сходимости; ряд (30.3) можно почленно интегрировать и дифференцировать внутри его интервала сходимости 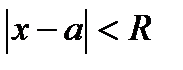 , т.е. если
, т.е. если 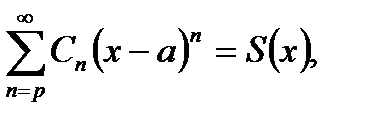 то для
то для 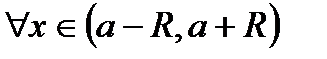 имеем
имеем  и
и 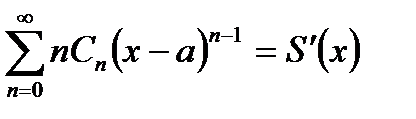
Нахождение суммы ряда почленным дифференцированием.
I. Пусть дан ряд вида 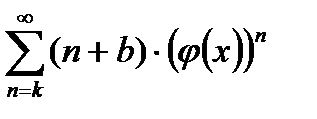 .
.
Сначала определяем область сходимости ряда, например, по признаку Коши. Получаем неравенство 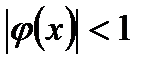 . Если
. Если  , то ряд расходится, т.к. не выполнено необходимое
, то ряд расходится, т.к. не выполнено необходимое
условие сходимости 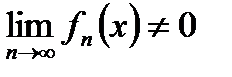 . Следовательно, область
. Следовательно, область
сходимости определяется неравенством 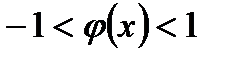 . Затем делаем замену
. Затем делаем замену 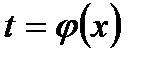 и записываем ряд в виде суммы двух рядов
и записываем ряд в виде суммы двух рядов 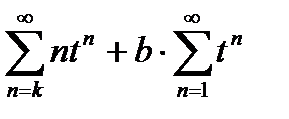 . Для нахождения сумм этих рядов используем формулу суммы членов бесконечно убывающей геометрической прогрессии и очевидное равенство
. Для нахождения сумм этих рядов используем формулу суммы членов бесконечно убывающей геометрической прогрессии и очевидное равенство
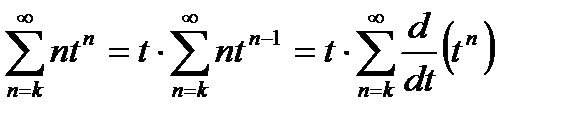 .
.
Учитывая, что степенной ряд можно почленно дифференцировать в любой точке интервала сходимости, и используя равенство
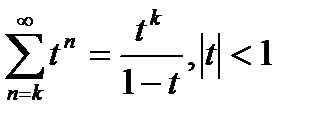 , получаем
, получаем
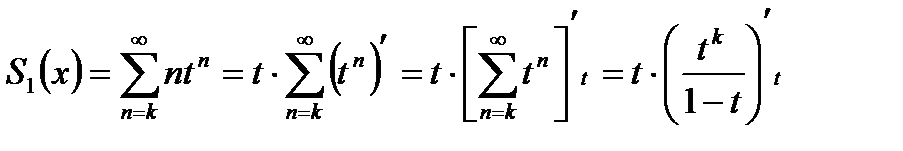
Далее вычисляем производную, делаем замену 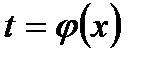
и записываем ответ.
II. Если дан ряд вида 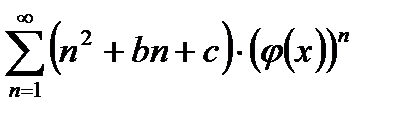 , то вычисляем сумму трех рядов
, то вычисляем сумму трех рядов  ,
, 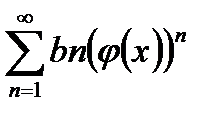 и
и 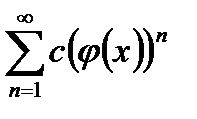 , при вычислении суммы ряда
, при вычислении суммы ряда  применяем теорему о почленном дифференцировании степенного ряда дважды.
применяем теорему о почленном дифференцировании степенного ряда дважды.
Пример 5. Найти сумму ряда и указать область
сходимости ряда к этой сумме. 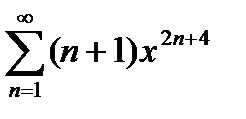
Решение. а). Находим область сходимости данного ряда по признаку Даламбера
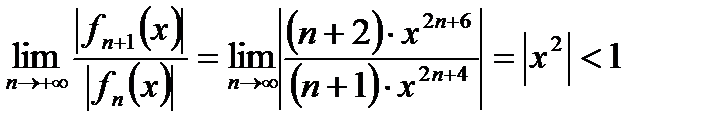
Отсюда 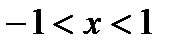 . В граничных точках
. В граничных точках 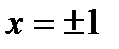 ряд расходится, т.к. не выполнено необходимое условие сходимости. Итак, ряд сходится (и притом абсолютно) в интервале (-1;1).
ряд расходится, т.к. не выполнено необходимое условие сходимости. Итак, ряд сходится (и притом абсолютно) в интервале (-1;1).
б). Делаем в исходном ряде замену 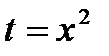 и записываем в виде суммы двух рядов
и записываем в виде суммы двух рядов 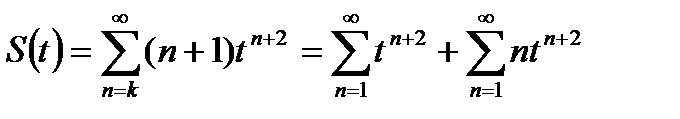
Для нахождения S(t) достаточно найти суммы рядов
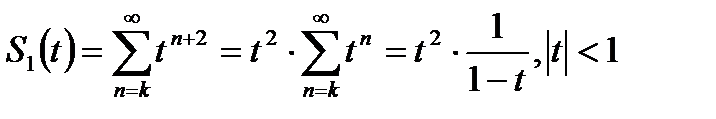 и
и
 .
.
Учитывая, что степенной ряд можно почленно
д
Дата: 2016-10-02, просмотров: 314.