Основные теоретические сведения
Область определения
Переменные x,y,z, …,t называются независимыми между собой, если каждая из них принимает любые значения в своей области изменения, независимо от того, какие значения принимают при этом остальные переменные. Переменная величина u называется однозначной функцией независимых переменных (аргументов) x,y,z,…,t, если каждой совокупности их значений (x,y,z …,t) из области D соответствует единственное определенное значение u 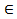 U. Функциональная зависимость обозначается так: u=f(x,y,z, …,t), или f: D→U, где U – множество значений функции f.
U. Функциональная зависимость обозначается так: u=f(x,y,z, …,t), или f: D→U, где U – множество значений функции f.
Областью определения (существования) D функции
u=f (x,y,z,…,t) называется совокупность значений x,y,z,…,t, при которых функция определена, то есть принимает определенные действительные значения. Так, для функции двух переменных z=f (x, y) областью определения является совокупность точек (x,y) координатной плоскости XOY, в которых функция определена (существует). Эта область определения представляет собой конечную или бесконечную часть плоскости XOY, ограниченную одной или несколькими кривыми (границей области D). Аналогично, для функции трех переменных u=f(x,y,z) областью определения служит некоторое тело в пространстве OXYZ.
Рассмотрим примеры нахождения областей
определения функций.
Пример 1. 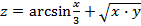
Решение. Первое слагаемое функции определено при 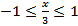 , или
, или 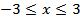 . Второе слагаемое имеет действительные значения, если
. Второе слагаемое имеет действительные значения, если 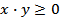 , то есть при
, то есть при 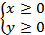 или при
или при 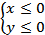 . Значит, область определения всей функции есть множество точек (x,y) двух полос плоскости XOY: При
. Значит, область определения всей функции есть множество точек (x,y) двух полос плоскости XOY: При 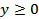 между прямыми x = 0, x = 3, y = 0 и при
между прямыми x = 0, x = 3, y = 0 и при 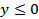 между прямыми
между прямыми
x = -3, x = 0, y = 0, включая сами эти прямые (рис. 21.1).
Рис. 21.1
Пример 2 . 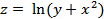 ,
,
Решение. Так как логарифм не существует при нуле и отрицательных значениях, то должно выполняться неравенство 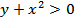 , то есть
, то есть 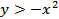 . Значит, область определения функции есть часть плоскости, расположенной над параболой
. Значит, область определения функции есть часть плоскости, расположенной над параболой 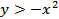 , не включая саму границу, то есть точки кривой
, не включая саму границу, то есть точки кривой 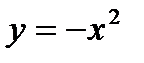 (рис. 21.2).
(рис. 21.2).
Рис. 21.2
Предел. Непрерывность.
Число А называется пределом функции 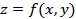 при стремлении точки М(x,y) к точке
при стремлении точки М(x,y) к точке 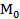 (a,b), если для любого
(a,b), если для любого
числа 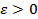 существует такое число δ
существует такое число δ 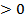 ,
, 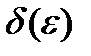 ,что при
,что при
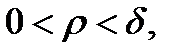 где
где 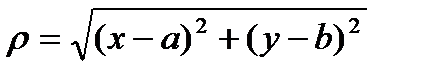 – расстояние между точками М и
– расстояние между точками М и 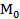 , имеет место неравенство
, имеет место неравенство 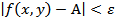 .
.
В этом случае пишут 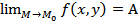 , или
, или 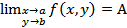 . Функция
. Функция 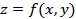 называется непрерывной в точке M0(a,b), если предел функции
называется непрерывной в точке M0(a,b), если предел функции 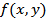 при стремлении точки M(x,y) к точке M0(a,b) равен значению функции
при стремлении точки M(x,y) к точке M0(a,b) равен значению функции 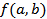 в точке Mo, то есть:
в точке Mo, то есть:
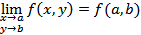
Функция, непрерывная во всех точках некоторой области, называется непрерывной в этой области.
Нарушение условий непрерывности для функции 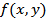 может быть как в отдельных точках (изолированная точка разрыва), так и в точках, образующих одну или несколько линий (линии разрыва).
может быть как в отдельных точках (изолированная точка разрыва), так и в точках, образующих одну или несколько линий (линии разрыва).
Пример 3 . Найти пределы следующих функций:
а) 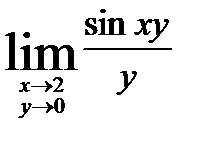 ; б)
; б) 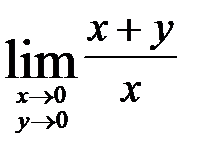 .
.
Решение:
а) 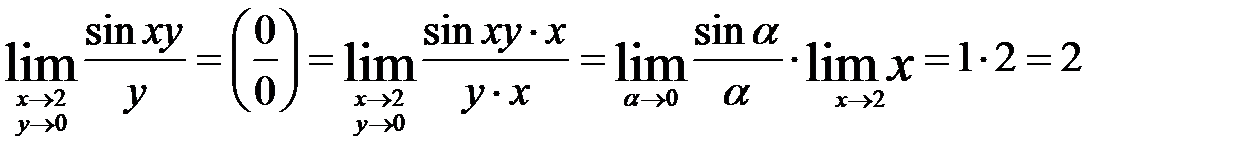 ,
,
где 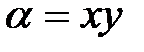 . Здесь выполняется первый замечательный предел
. Здесь выполняется первый замечательный предел 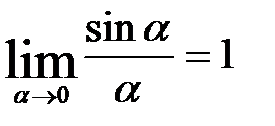 .
.
б) 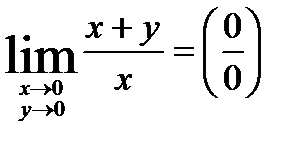 . Рассмотрим изменение переменных
. Рассмотрим изменение переменных 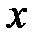 и
и 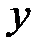 вдоль прямых
вдоль прямых 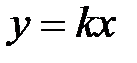 ]
] 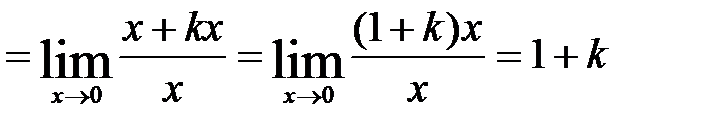 . Так как данное выражение
. Так как данное выражение 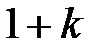 может принимать различные значения в зависимости от числа
может принимать различные значения в зависимости от числа 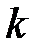 , то предела не существует.
, то предела не существует.
Линии и поверхности уровня функции.
Линией уровня функции двух аргументов 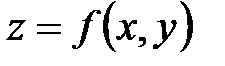 называется такая линия
называется такая линия 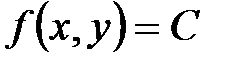 на плоскости XOY, в точках которой функция принимает одно и то же значение
на плоскости XOY, в точках которой функция принимает одно и то же значение 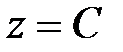 , где C – const.
, где C – const.
Поверхностью уровня функции трех аргументов 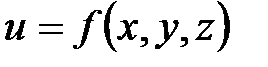 называется такая поверхность
называется такая поверхность 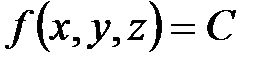 , в точках которой функция принимает постоянное значение
, в точках которой функция принимает постоянное значение 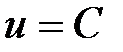 .
.
Пример 4. Выяснить характер поверхностей, изображаемых следующими функциями и построить их линии уровня:
а) 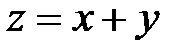 ; б)
; б) 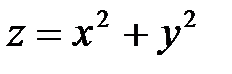 ; в)
; в) 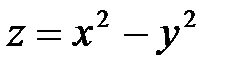 .
.
Решение: а) плоскость; линии уровня – семейство прямых 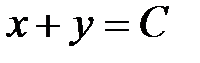 , параллельных прямой
, параллельных прямой 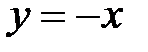 , (при
, (при 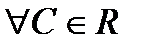 ).
).
б) параболоид вращения; линии уровня 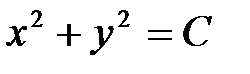 – семейство концентрических окружностей с центром в начале координат (
– семейство концентрических окружностей с центром в начале координат ( 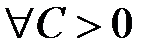 ).
).
в) гиперболический параболоид; линии уровня 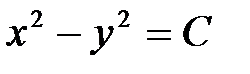 - семейство равносторонних гипербол
- семейство равносторонних гипербол 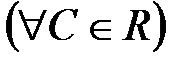 .
.
Дополнительные сведения.
Часть пространства, в котором происходит физическое явление, называется физическим полем. Существуют скалярное и векторное поля.
Физическое поле называется скалярным, если физическое явление, его образующее, характеризуется функцией 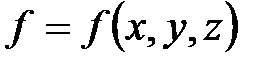 , зависящей только от координат точек пространства, в котором это явление происходит. Скалярное поле полностью определено заданием одной функцией
, зависящей только от координат точек пространства, в котором это явление происходит. Скалярное поле полностью определено заданием одной функцией 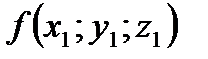 трех независимых переменных. Если физическое явление образовало скалярное поле, то каждой точке
трех независимых переменных. Если физическое явление образовало скалярное поле, то каждой точке 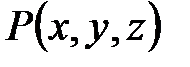 пространства
пространства 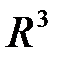 , в котором происходит это явление, ставится в соответствие определенное число, характеризующее это явление в рассматриваемой точке. Это число есть частное значение функции
, в котором происходит это явление, ставится в соответствие определенное число, характеризующее это явление в рассматриваемой точке. Это число есть частное значение функции 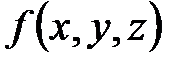 , вычисленное в точке
, вычисленное в точке 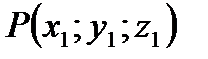 .
.
Примерами скалярного поля являются: поле электрического потенциала, давление в атмосфере и т.п. В скалярном поле поверхность уровня называется эквипотенциальной поверхностью, во все точках которой однозначная функция 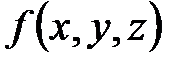 сохраняет одно и то же значение. Через каждую точку пространства проходит одна поверхность уровня. Во всех точках поверхности уровня физическое явление протекает одинаково. Уравнение поверхности уровня, проходящей через точку
сохраняет одно и то же значение. Через каждую точку пространства проходит одна поверхность уровня. Во всех точках поверхности уровня физическое явление протекает одинаково. Уравнение поверхности уровня, проходящей через точку 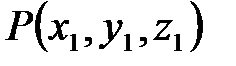 , имеет вид
, имеет вид 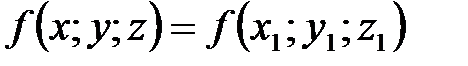 .
.
Дата: 2016-10-02, просмотров: 319.