И наименьшее значения функции
В замкнутой области
Условный экстремум.
Во многих задачах на отыскание экстремума функции ее переменные оказываются не независимыми переменными, а связанными друг с другом некоторыми добавочными условиями (так называемыми уравнениями связи). Здесь мы имеем дело с задачами на условный экстремум.
Условным экстремумом функции 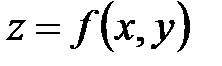 двух переменных называется максимум или минимум этой функции, достигнутый при условии, что аргументы x, y связаны уравнением
двух переменных называется максимум или минимум этой функции, достигнутый при условии, что аргументы x, y связаны уравнением 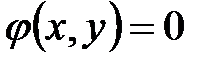 (уравнение связи). Для отыскания условного экстремума функции
(уравнение связи). Для отыскания условного экстремума функции 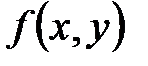 при наличии уравнения связи
при наличии уравнения связи 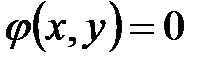 применяют метод Лагранжа:
применяют метод Лагранжа:
Составляют функцию Лагранжа. Обозначается Ф или L.
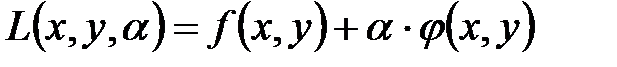 где
где 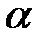 - неопределенный постоянный множитель, и ищут обычный экстремум этой вспомогательной функции
- неопределенный постоянный множитель, и ищут обычный экстремум этой вспомогательной функции 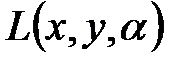 .
.
Необходимые условия экстремума функции Лагранжа имеют вид
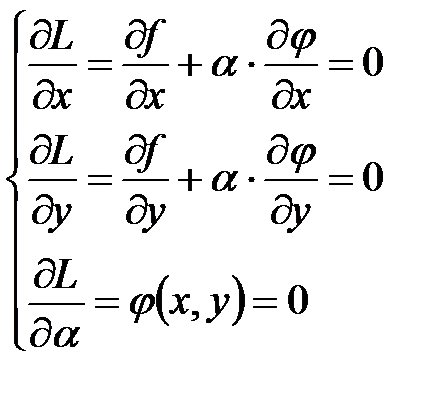
Из этой системы трех уравнений можно найти неизвестные x, y и 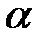 . Вопрос о существовании и характере условного экстремума решается на основании изучения знака второго дифференциала функции Лагранжа
. Вопрос о существовании и характере условного экстремума решается на основании изучения знака второго дифференциала функции Лагранжа
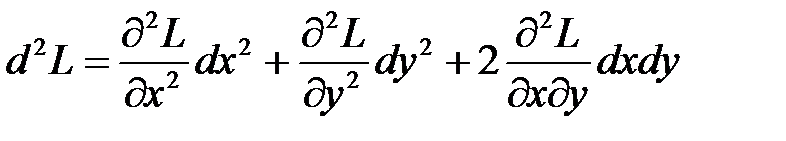 , для найденных значений x, y и
, для найденных значений x, y и 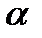 , полученных из системы уравнений , при условии, что dx и dy связаны уравнением
, полученных из системы уравнений , при условии, что dx и dy связаны уравнением
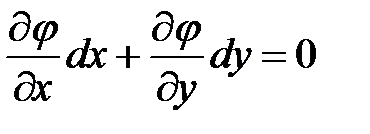
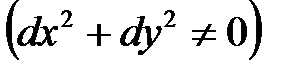 .
.
А именно, функция 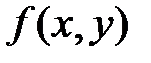 имеет условный максимум, если
имеет условный максимум, если 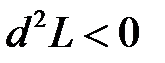 и условный минимум, если
и условный минимум, если 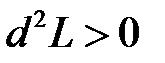 .
.
В частности, если дискриминант 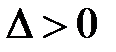 для функции Лагранжа в стационарной точке, то в этой точке имеется условный экстремум данной функции
для функции Лагранжа в стационарной точке, то в этой точке имеется условный экстремум данной функции 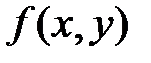 , причем условный максимум
, причем условный максимум 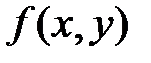 , если А<0 (или С<0 ), и условный минимум
, если А<0 (или С<0 ), и условный минимум 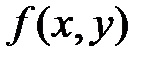 , если A>0 (C >0), где
, если A>0 (C >0), где
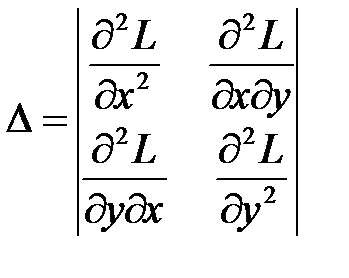 .
.
Аналогично находится условный экстремум функции трех и большего числа переменных при наличии одного или нескольких уравнений связи (число которых, однако, должно быть меньше числа переменных). Здесь приходится вводить в функцию Лагранжа столько неопределённых множителей, сколько имеется уравнений связи.
Пример 1 . Определить условный экстремум функции
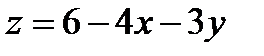 при условии
при условии 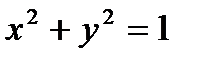 .
.
Решение. Геометрически данная задача сводиться к нахождению наибольшего и наименьшего значений аппликаты 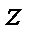 плоскости
плоскости 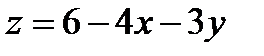 для точек пересечения её с прямым круговым цилиндром
для точек пересечения её с прямым круговым цилиндром 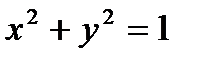 . Составим функцию Лагранжа
. Составим функцию Лагранжа 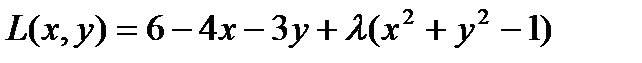 , где
, где 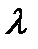 -неопределённый множитель;
-неопределённый множитель; 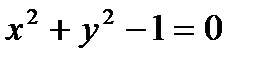 - уравнение связи.Находим
- уравнение связи.Находим 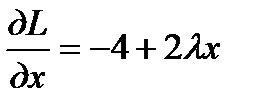 ,
, 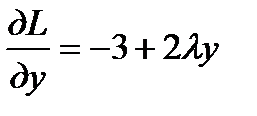 .Необходимые условия экстремума для функции
.Необходимые условия экстремума для функции  получаем из следующей системы уравнений
получаем из следующей системы уравнений 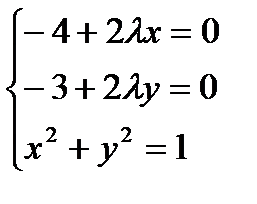
Решая эту систем, получаем два решения 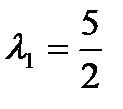 ,
, 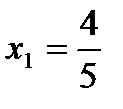 ,
, 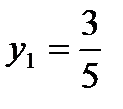 и
и 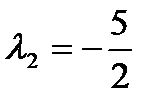 ,
, 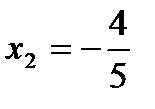 ,
, 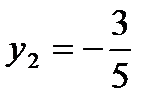 . Далее, находим
. Далее, находим 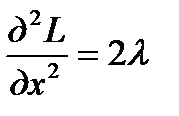 ,
, 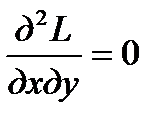 ,
, 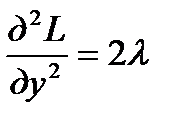 . Значит,
. Значит, 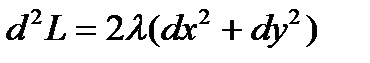 .
.
При 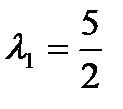 ,
, 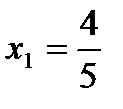 ,
, 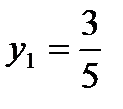 имеем
имеем 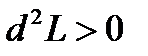 и, следовательно, в этой точке функция имеет условный минимум:
и, следовательно, в этой точке функция имеет условный минимум: 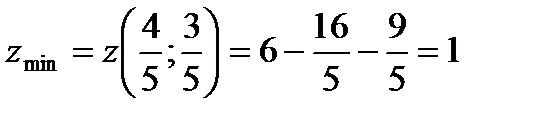 .
.
При 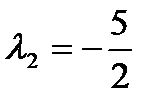 ,
, 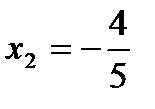 ,
, 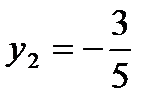 имеем
имеем 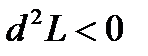 и, следовательно, в этой точке функция имеет условный максимум:
и, следовательно, в этой точке функция имеет условный максимум: 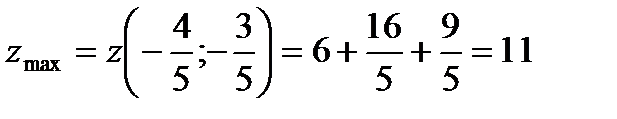 .
.
Нахождение наибольшего и наименьшего
значений функции в замкнутой области.
Функция, непрерывная в ограниченной замкнутой области, достигает в ней своего наибольшего и наименьшего значений или во внутренних точках этой области, являющимися стационарными точками или в точках, лежащих на границе области. Для того, чтобы найти наибольшее и наименьшее значения функции в замкнутой области, надо:
1) Найти стационарные точки, расположенные внутри данной области, и вычислить значения функции в этих точках;
2) Найти наибольшее и наименьшее значения функции на линиях, образующих границу области;
3) Из всех найденных значений выбрать наибольшее и наименьшее.
Замечание 1. В данном случае нет необходимости исследовать функцию на экстремум с помощью частных производных второго порядка. Требуется найти лишь стационарные точки и значения функции в них.
Замечание 2. Для функции 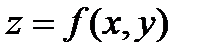 линии границы области являются функцией одной переменной: либо
линии границы области являются функцией одной переменной: либо  ,
, 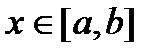 , либо
, либо 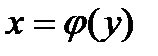 ,
, 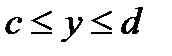 ,
,
поэтому на соответствующих участках границы данная функция является функцией одной переменной.
Несколько уравнений связи (число которых, однако, должно быть меньше числа переменных). Здесь приходиться вводить в функцию Лагранжа столько неопределённых множителей, сколько имеется уравнений связи.
Пример 2 .Найти наибольшее и наименьшее значения функции 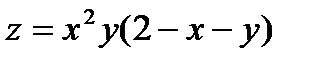 внутри замкнутого треугольника
внутри замкнутого треугольника 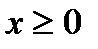 ,
, 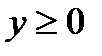 ,
, 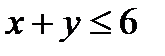 (рис.26.1).
(рис.26.1).
Решение.1) Находим стационарные точки внутри  . Имеем : частные производные
. Имеем : частные производные 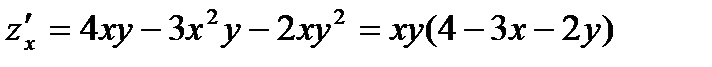 ;
;
Рис. 26.1
Приравнивая эти производные к нулю, получим систему уравнений:
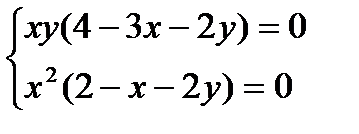
Так как 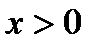 ,
, 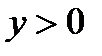 для нахождения стационарных точек внутри
для нахождения стационарных точек внутри 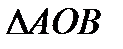 , имеем систему
, имеем систему 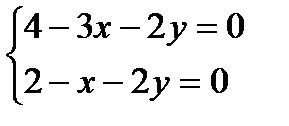 , откуда
, откуда 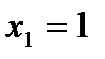 ;
; 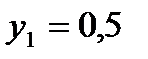 , из которой находим единственную стационарную точку
, из которой находим единственную стационарную точку 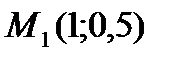 , где значение функции
, где значение функции 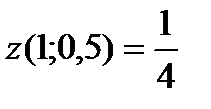 .
.
2) Переходим к исследованию функции 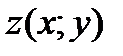 на границах области, которая состоит из отрезков ОА оси ОХ, ОВ оси ОУ и отрезка АВ прямой.
на границах области, которая состоит из отрезков ОА оси ОХ, ОВ оси ОУ и отрезка АВ прямой.
а) На оси ОХ отрезок ОА: 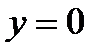 , и заданная функция
, и заданная функция 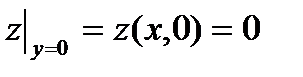 ,
, 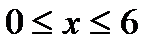 ; аналогично, на оси ОУ отрезок ОВ:
; аналогично, на оси ОУ отрезок ОВ: 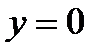 , где также заданная функция
, где также заданная функция 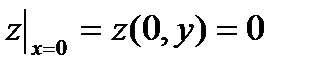 ,
, 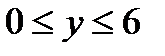 .
.
б) Исследуем функцию на отрезке АВ: где прямая АВ задана уравнением 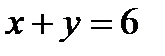 ,
, 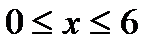 . Поэтому функция на этой прямой будет зависеть от одной переменной х, где
. Поэтому функция на этой прямой будет зависеть от одной переменной х, где 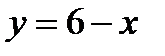 :
:
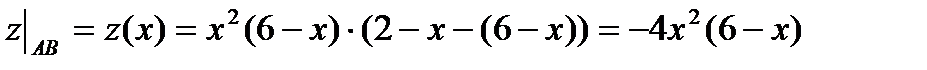 ,
, 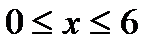 .
.
На концах отрезка [0,6]: 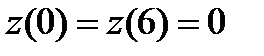 .
.
Находим критические точки функции 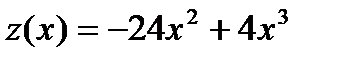 .
.
Имеем 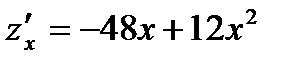 . Решая уравнение
. Решая уравнение 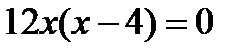 , получаем
, получаем 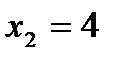 ; соответственно,
; соответственно, 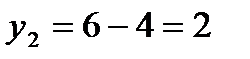 . Итак
. Итак 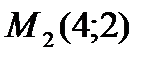 -критическая точка на отрезке АВ; значение функции
-критическая точка на отрезке АВ; значение функции 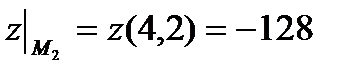 . Следовательно,
. Следовательно, 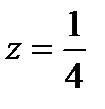 внутри
внутри 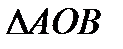 в точке
в точке 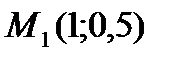 ;
; 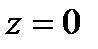 на сторонах ОВ и ОА и в вершинах
на сторонах ОВ и ОА и в вершинах 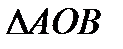 ;
; 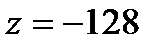 на стороне АВ. Итак, наибольшего значения функция достигла
на стороне АВ. Итак, наибольшего значения функция достигла 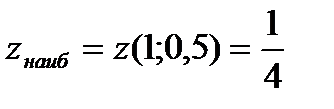 в точке
в точке 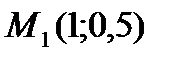 , а наименьшего значения
, а наименьшего значения 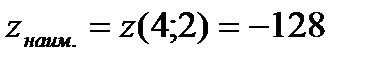 на границе области в точке
на границе области в точке 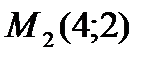 .
.
Дифференциальные уравнения
Основные понятия
Дифференциальным уравнением называют уравнение типа
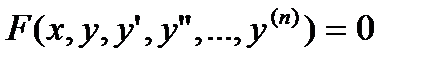 , (27.1)
, (27.1)
где х - независимая переменная, 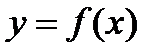 -искомая функция,
-искомая функция, 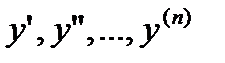 -ее производные. Решением дифференциального уравнения (27.1) называется такая функция
-ее производные. Решением дифференциального уравнения (27.1) называется такая функция 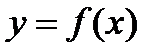 , которая при подстановке ее и ее производных обращает равенство в (27.1) в тождество. Порядком дифференциального уравнения (27.1) называется наибольший порядок n входящей в него производной. Интегрированием дифференциального уравнение называется процесс нахождения его решения. Общим решением дифференциального уравнения (27.1) порядка n называется такое решение
, которая при подстановке ее и ее производных обращает равенство в (27.1) в тождество. Порядком дифференциального уравнения (27.1) называется наибольший порядок n входящей в него производной. Интегрированием дифференциального уравнение называется процесс нахождения его решения. Общим решением дифференциального уравнения (27.1) порядка n называется такое решение  , которые являются функцией от независимой переменной х и от n произвольных независимых постоянных
, которые являются функцией от независимой переменной х и от n произвольных независимых постоянных 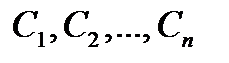 .Частным решением называется решение, полученное из общего решения при конкретных значениях постоянных
.Частным решением называется решение, полученное из общего решения при конкретных значениях постоянных 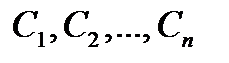 . Привести дифференциальное уравнение к квадратурам означает преобразовать это уравнение до вычисления интегралов (уравнение вычисляется в квадратурах).
. Привести дифференциальное уравнение к квадратурам означает преобразовать это уравнение до вычисления интегралов (уравнение вычисляется в квадратурах).
Дифференциальное уравнение первого порядка
Разрешением относительно производной называется
дифференциальное уравнение первого порядка 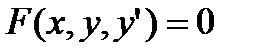
которое можно записать в виде
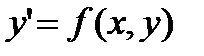 . (27.2)
. (27.2)
Уравнение с разделяющимися переменными.
Решение уравнений вида (27.2) сводится к нахождению
неопределенных интегралов, если функция двух переменных 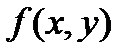 представима в виде произведения двух функций одной переменной
представима в виде произведения двух функций одной переменной 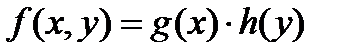 .
.
Заменяя 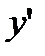 на
на 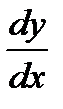 , из (27.2) получаем
, из (27.2) получаем
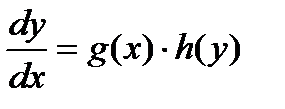 (27.3)
(27.3)
Уравнением с разделяющимися переменными называются уравнения вида (27.3). По-другому такие уравнения можно записать в виде
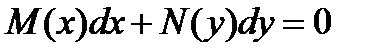 (27.4)
(27.4)
или
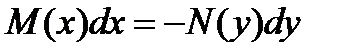 .
.
Интегрируя обе части последнего неравенства, получаем
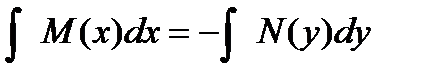 .
.
Общим интегралом дифференциального уравнения называется его решение, которое находится в виде 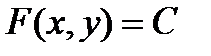 или
или 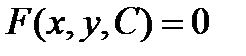 .
.
Однородные уравнения и уравнения,
приводящие к однородным
Однородной функцией порядка 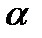 называется функция
называется функция 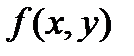 , удовлетворяющая условию
, удовлетворяющая условию 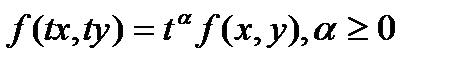 . Однородным дифференциальным уравнением первого порядка называется уравнение
. Однородным дифференциальным уравнением первого порядка называется уравнение 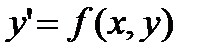 , где
, где 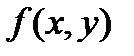 -однородная функция нулевого порядка. Заменой
-однородная функция нулевого порядка. Заменой
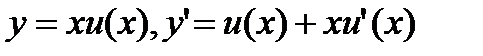 (27.5)
(27.5)
Оно становится к уравнению с разделяющимися переменными. К однородным сводятся уравнения вида
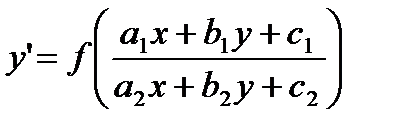 (27.6)
(27.6)
С помощью замены
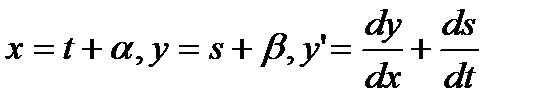 . (27.7)
. (27.7)
Пример 1. Найти общий интеграл
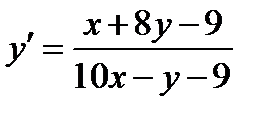 ,
,
Решение.
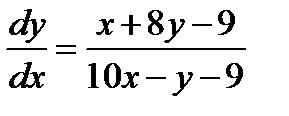 ,
, 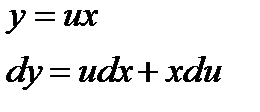
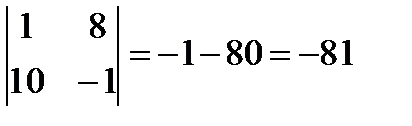 ,
, 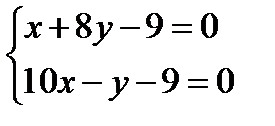 ,
, 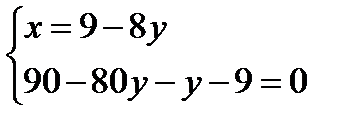 .
.
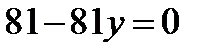 ,
, 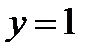 ,
, 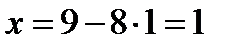 ,
, 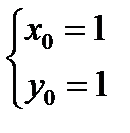 ,
, 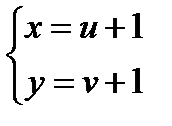 .
. 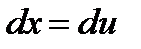 .
.
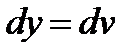 ,
, 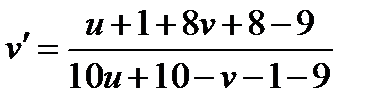 ,
, 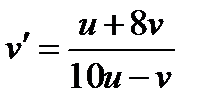 ,
, 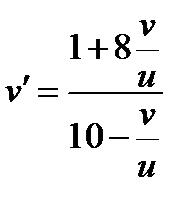 .
.
Делаем замену 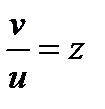 ,
, 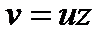 ,
, 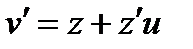 ,
, 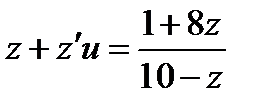 ,
,
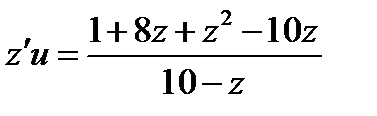 и
и 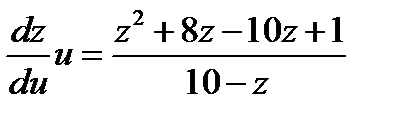 ,
, 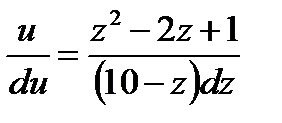 ,
,
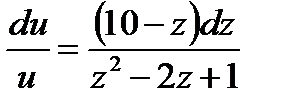 ,
, 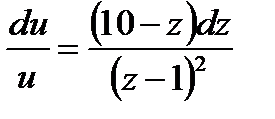 и
и 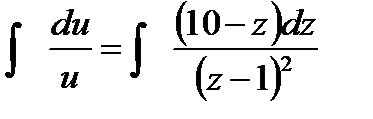 т.е.
т.е.
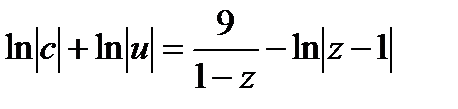 ,
, 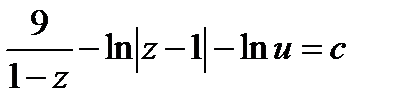 ,
,
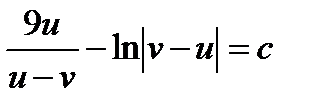 . Ответ:
. Ответ: 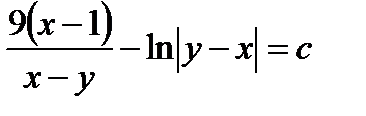
Уравнение Бернулли
Уравнением Бернулли называется уравнение
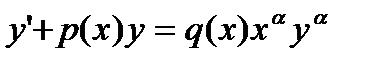 . (27.8)
. (27.8)
Для интегрирования этого уравнения сделаем замену
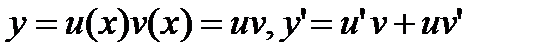 . (27.9)
. (27.9)
Таким образом вместо одной независимой функции вводятся две. При этом появляется возможность выбрать одну из функций 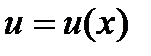 или
или 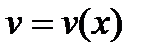 исходя из соображений удобства. Подставим y и y’ в дифференциальное уравнение. Получим
исходя из соображений удобства. Подставим y и y’ в дифференциальное уравнение. Получим 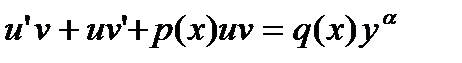 , или
, или
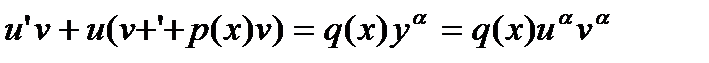 .
.
Положим 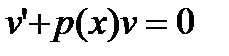 , тогда получим уравнение с
, тогда получим уравнение с
разделяющимися переменными 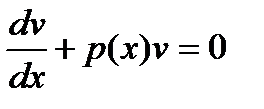 .
.
Проинтегрировав это уравнение, найдем функцию 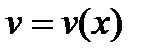 . Подставив ее в уравнение, получим дифференциальное уравнение относительно функции
. Подставив ее в уравнение, получим дифференциальное уравнение относительно функции 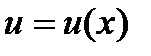 , после интегрирования которого найдем искомую функцию
, после интегрирования которого найдем искомую функцию 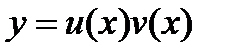 .
.
Пример 2. Решить задачу Коши:
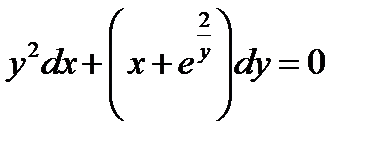 ,
, 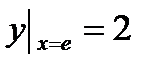
Решение.
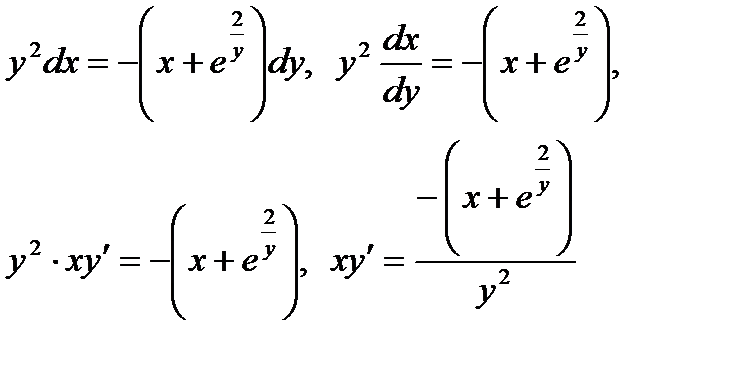
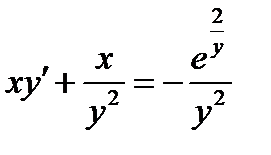
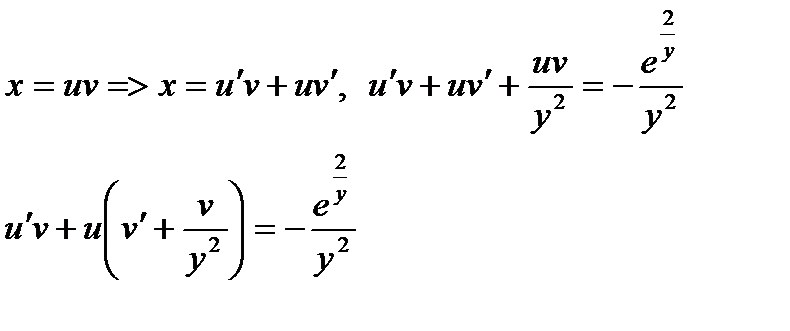
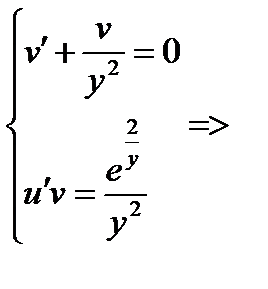
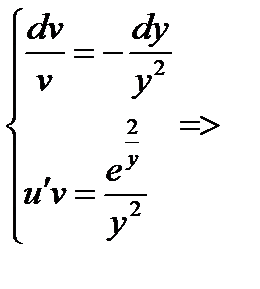
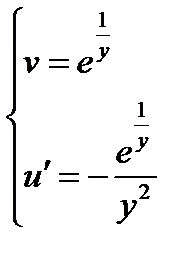 = >
= >
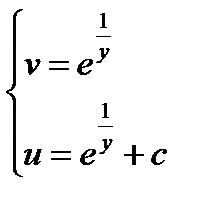 =>
=> 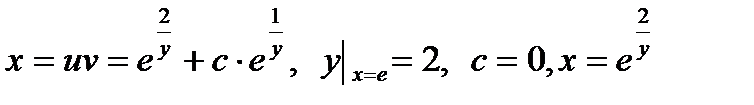
Ответ: 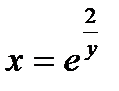
Уравнение в полных дифференциалах.
Уравнением в полных дифференциалах называется уравнение
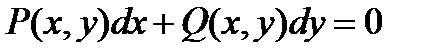 , (27.10)
, (27.10)
где левая часть представляет собой полный дифференциал
некоторой функции 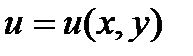 , т. е.
, т. е.
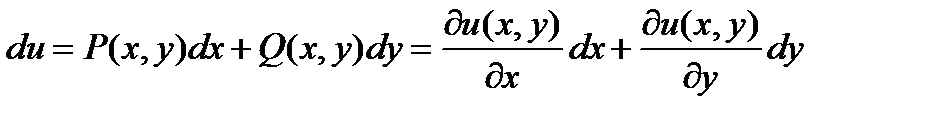 ,
,
или
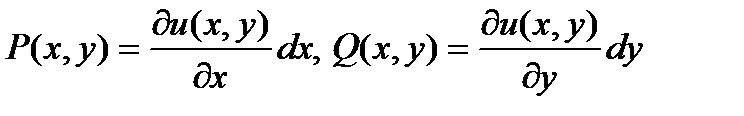 .
.
Из первого из этих уравнений находим
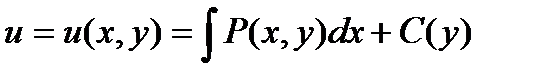 .
.
Можно доказать, что если выполнено условие
 , (27.11)
, (27.11)
то Pdx+Qdy=0 уравнение в полных дифференциалах.
Пример 3. Найти общий интеграл:
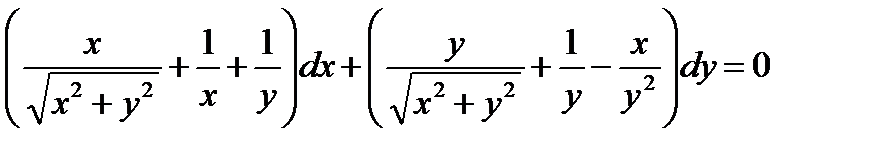
Решение.
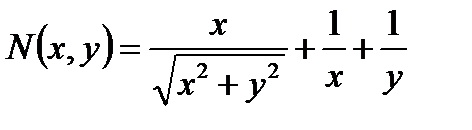
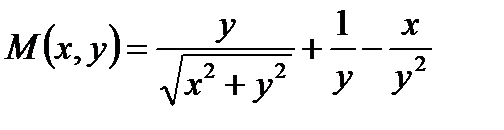
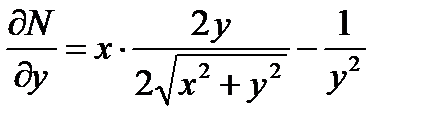 ,
, 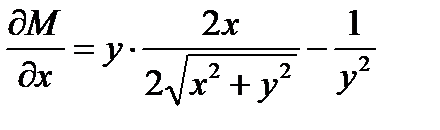
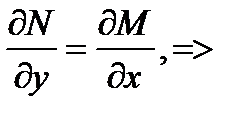 данное уравнение в полных дифференциалах
данное уравнение в полных дифференциалах
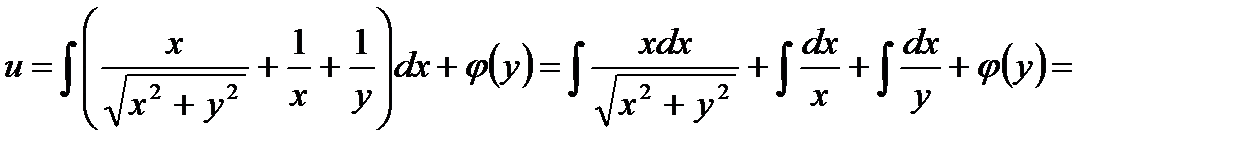
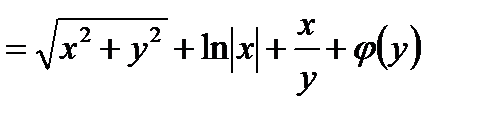 .
.
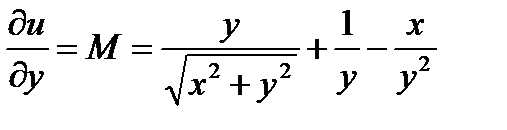
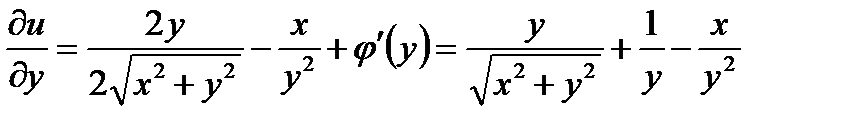 ,
,
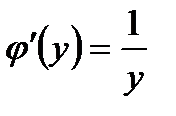 ,
, 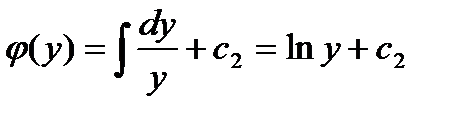 ,
,
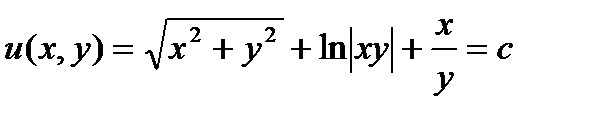
Ответ: 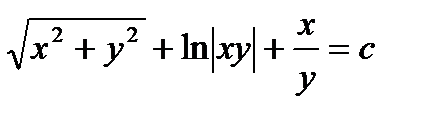
Линейные уравнения первого порядка
Линейным дифференциальным уравнением первого
порядка называется уравнение вида
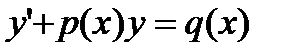 . (27.12)
. (27.12)
Уравнение (27.12) называется однородным, еслиq(x)=0.
Решение уравнения (27.12) ищутся в виде произведения
двух неизвестных функций 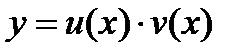 . Так как
. Так как
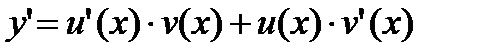 , то из (12) следует, что
, то из (12) следует, что
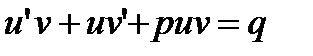 или
или
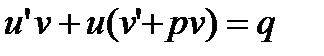 (27. 13)
(27. 13)
Выберем функцию 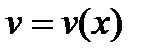
такой, чтобы выполнялось равенство
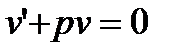 . (27.14)
. (27.14)
Это возможно сделать, решая уравнение (27.14) с разделяющимися переменными. После выбора функции 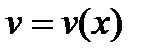 уравнение (27.13) примет вид
уравнение (27.13) примет вид 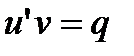 . Это уравнения является также решением уравнением с разделяющимися переменными. Интегрируя его, находим функцию
. Это уравнения является также решением уравнением с разделяющимися переменными. Интегрируя его, находим функцию 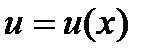 .
.
Тогда функция 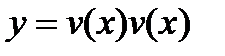 будет решением уравнения (27.12). Таким образом, интегрирование линейного дифференциального уравнения первого порядка сводится к интегрированию двух уравнений с разделяющимися переменными.
будет решением уравнения (27.12). Таким образом, интегрирование линейного дифференциального уравнения первого порядка сводится к интегрированию двух уравнений с разделяющимися переменными.
Дифференциальные уравнения высших порядков
Дифференциальным уравнением n-го порядка называется уравнение вида 
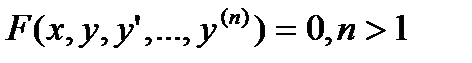 .
.
Разрешенным относительно старшей производной
называется уравнение 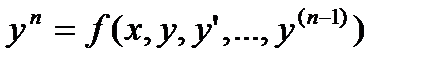 .
.
Условиями Коши или начальными условиями для
уравнения n-го порядка называются соотношения
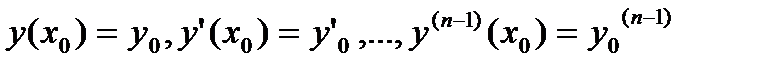 , (27.15)
, (27.15)
где х0, у0, у’0,…,y0(n-1)-заданные числа. Задача нахождение дифференциального уравнения, удовлетворяющего заданным начальным условием, называется задачей Коши. Некоторые уравнения высших порядков допускают понижение порядка. Для примера рассмотрим дифференциальные уравнения второго порядка:
a) 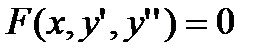
б) 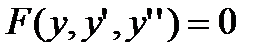 .
.
В случае а замена 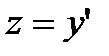 ,
, 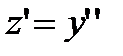 приводит к уравнению
приводит к уравнению
первого порядка 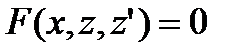 ; в случае б) замена
; в случае б) замена
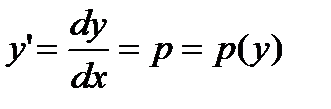 ,
, 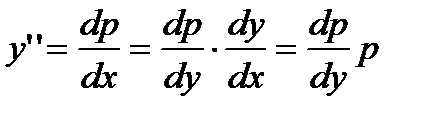 .
.
Также имеем уравнение первого порядка 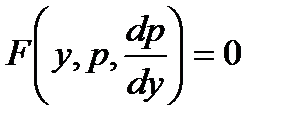 .
.
Пример 4. Найти решение задачи Коши.
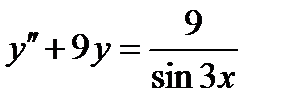 ,
, 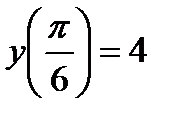 ,
, 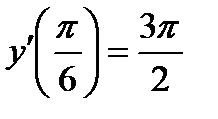 .
.
Решение.
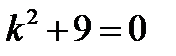 ,
, 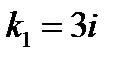 ,
, 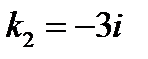 .
.
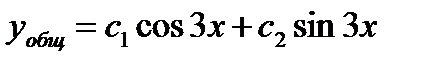
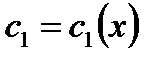 ,
, 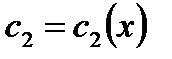 .
.
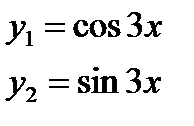 ,
, 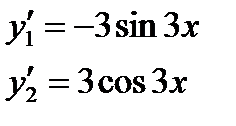 . Пусть
. Пусть 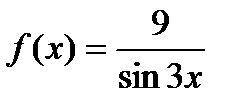 .
.
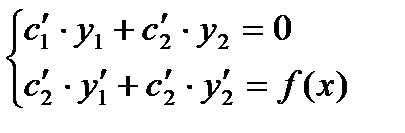 ,
, 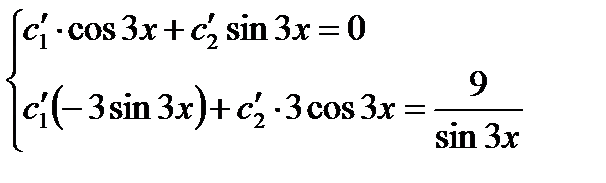
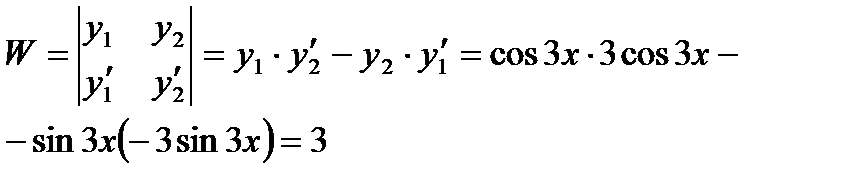
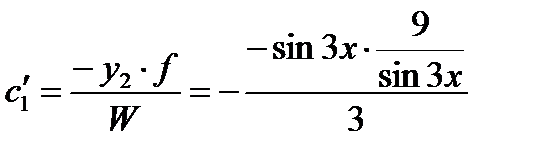 ,
, 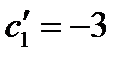 ,
, 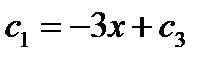 .
.
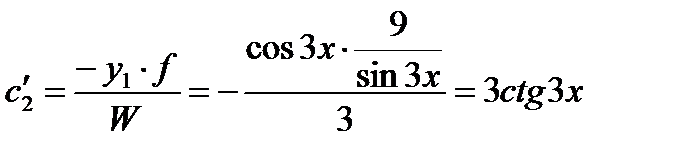 ,
,
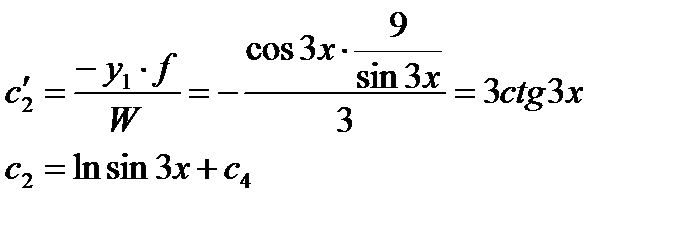 ,
,
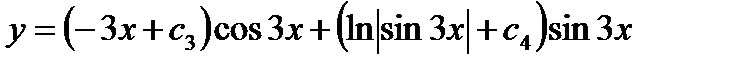 .
.
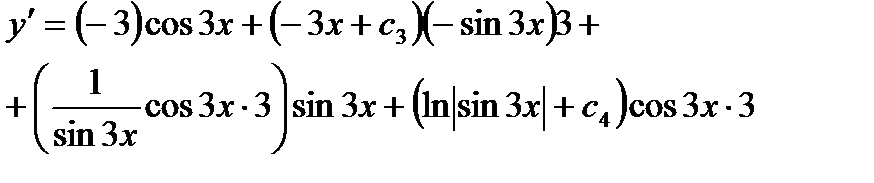
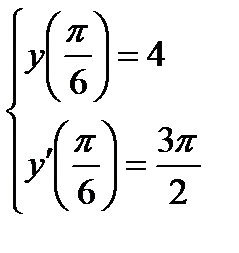 ,
, 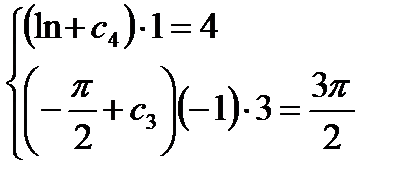 ,
, 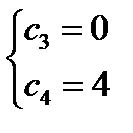 .
.
Ответ: 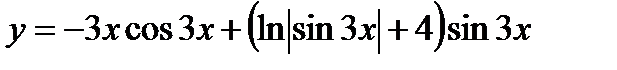
Линейные дифференциальные уравнения второго
порядка с постоянными коэффициентами
Линейным дифференциальным уравнением второго
порядка с постоянными коэффициентам называется
уравнение вида
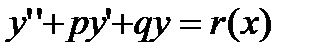 , (27.16)
, (27.16)
где p, q- некоторые числа; r(x)-функция от х.
Однородным линейным дифференциальным уравнением второго порядка с постоянными коэффициентами
называется уравнение (27.16), в котором правая часть
r(х) равна нулю:
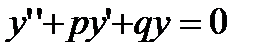 . (27.17)
. (27.17)
Общее решение уравнения (27.16) равно сумме какого
либо частного решения этого уравнения и общего
решения соответствующего однородного уравнения (27.17). Опишем сначала способ нахождения общего решения однородного уравнения (27.17).
Характеристическим уравнением для однородного
Уравнения (27.17) называется квадратное уравнение
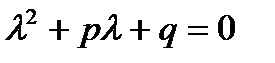
 (27.18)
(27.18)
Относительно неизвестной 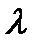 . В соответствии со знаком дискриминанта D=p2-4q возможны три случая:
. В соответствии со знаком дискриминанта D=p2-4q возможны три случая:
1) D>0: характеристическое уравнение имеет два
различных корня 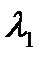 и
и 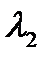 ;
;
2) D=0: характеристическое уравнение имеет один
корень 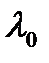 ;
;
3) D<0: действительных корней характеристическое
Уравнение не имеет. В этом случае находятся числа
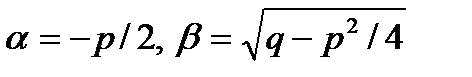 .
.
Найдем решение уравнения (27.17) для всех этих случает.
1. Если характеристическое уравнение (27.18) имеет
два различных корня 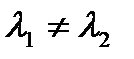 , то общее решение уравнения (27.17) имеет вид
, то общее решение уравнения (27.17) имеет вид
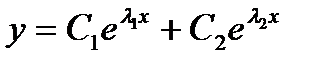 , (27.19)
, (27.19)
где С1, С2—произвольные постоянные.
2. Если характеристическое уравнение (27.18) имеет единственный корень 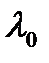 , то общее решение уравнения (27.17) имеет вид
, то общее решение уравнения (27.17) имеет вид
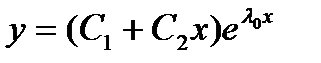 (27.20)
(27.20)
где С1, С2—произвольные постоянные.
3. характеристическое уравнение (27.18) не имеет корней,
то общее решение уравнения (27.17) имеет вид
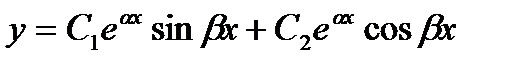 , (27.21)
, (27.21)
где С1, С2—произвольные постоянные. 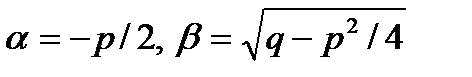 . Способы нахождения частных решений неоднородного уравнения (27.16) зависят от вида правой части и в явном виде находятся только для функций f(x) специального вида. Пусть f(x) имеет вид
. Способы нахождения частных решений неоднородного уравнения (27.16) зависят от вида правой части и в явном виде находятся только для функций f(x) специального вида. Пусть f(x) имеет вид
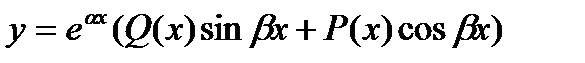 , (27.22)
, (27.22)
где 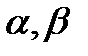 - некоторые числа, причем
- некоторые числа, причем 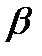 не равно нулю, Q(x), P(x)-многочлены от х. В этом случае частное решение уравнения (27.16) ищется в виде
не равно нулю, Q(x), P(x)-многочлены от х. В этом случае частное решение уравнения (27.16) ищется в виде
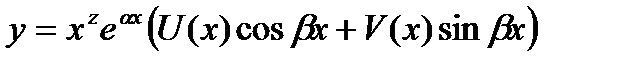 , (27.23)
, (27.23)
где U(x),V(x)-многочлены, степени которых равны наибольшей из степеней многочленов P(x) и Q(x). При этом показатель s выбирается по следующему правилу:
1) z=0, если
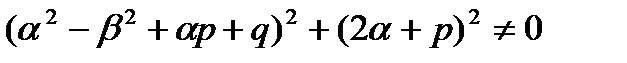 ; (27.24)
; (27.24)
2) z=1
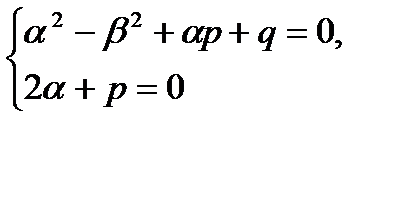 (27.25)
(27.25)
Многочлены U(x) и V(x) указанной степени в формуле (27.23) записываются в общем виде с произвольными коэффициентами. Затем находится производные y’ и y’’ функции (27.23). После подстановки y, y’ и y’’ в уравнение (27.16) получается линейная система уравнений для определения коэффициентов многочленов U(x) и V(x). Пусть правая часть уравнения (27.16) имеет вид
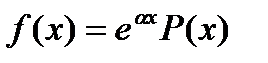 , (27.26)
, (27.26)
где 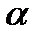 -некоторое число, Р(х)- многочлен от х (этот случай получается из (27.22) при
-некоторое число, Р(х)- многочлен от х (этот случай получается из (27.22) при 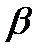 =0).Частное решение уравнения (27.16) ищется в виде
=0).Частное решение уравнения (27.16) ищется в виде
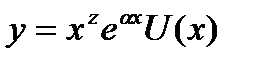 , (27.27)
, (27.27)
где U(x)-многочлен с неопределенными коэффициентами,
степень которого равна степени многочлена Р(х). При этом
показатель z выбирается по следующему правилу:
1) Z=0, если
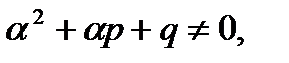 (27.28)
(27.28)
2) Z=1
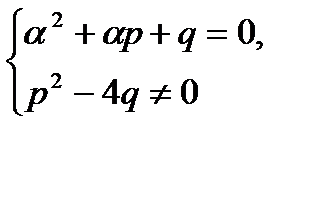 (27.29)
(27.29)
3) Z=2
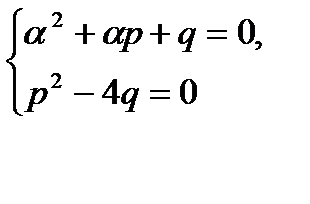 (27.30)
(27.30)
Пример 5 . Найти общее решение уравнения:
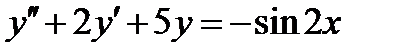
Решение.
Найдем общее решение однородного уравнения
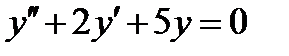
Составим и решим характеристическое уравнение
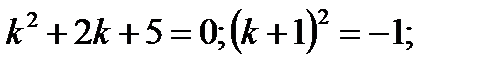
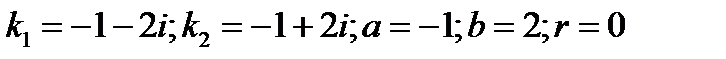
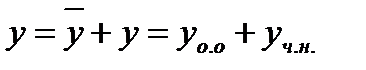
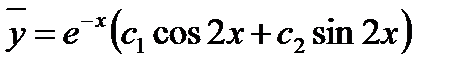
Частное решение неоднородного уравнения ищем в виде
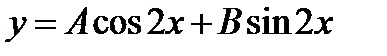
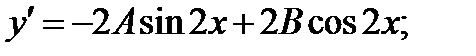
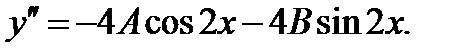
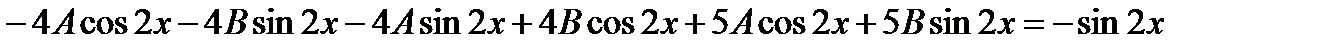
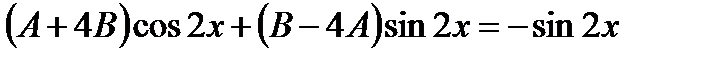
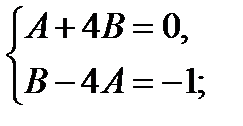
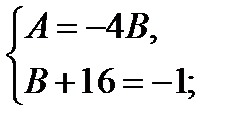
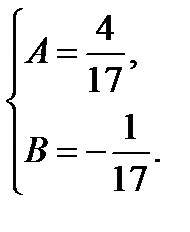
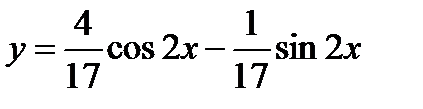
Общее решение данного уравнения
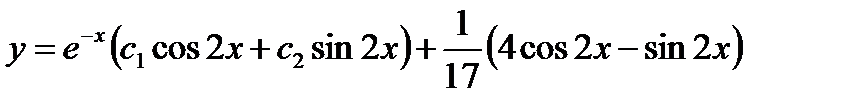
Ответ: 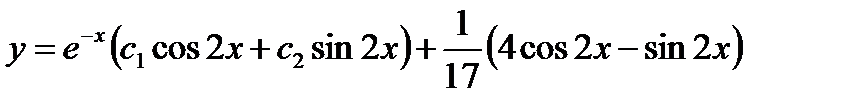
Линейные дифференциальные уравнения n-го порядка
с постоянными коэффициентами
Линейные дифференциальные уравнения n-го порядка
с постоянными коэффициентами решаются также, как и уравнения 2-го, но с учетом порядка уравнения (см. пример 6)
Пример 6 . Найти общее решение уравнения:
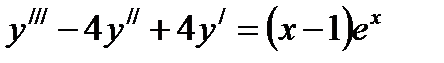
Решение.
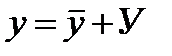 ,
, 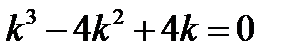 - характеристическое ур-е,
- характеристическое ур-е,
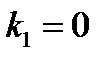 ,
, 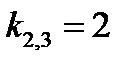 ,
, 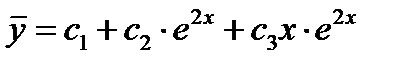 - общее решение однородного уравнения
- общее решение однородного уравнения
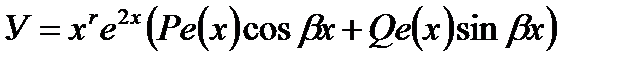
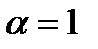 ,
, 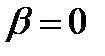 ,
, 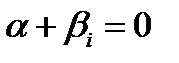 ,
, 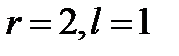
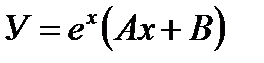 ,
, 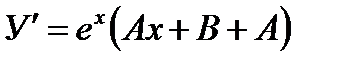
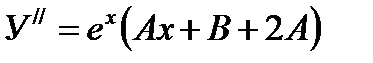 ,
, 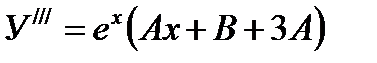
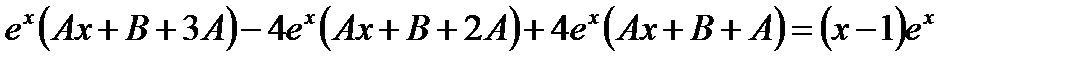 ,
,
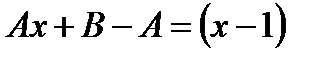
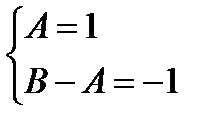
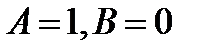 ,
, 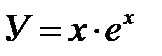 ,
, 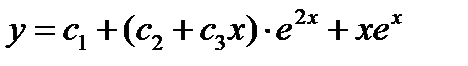
Ответ: 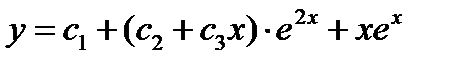
Линейные дифференциальные уравнения второго
порядка с переменными коэффициентами.
Уравнение
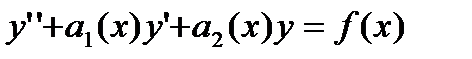 (27.31)
(27.31)
Представляет собой общий вид дифференциального уравнения второго порядка с правой частью f(x). Здесь 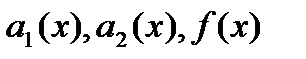 -некоторые непрерывные функции.
-некоторые непрерывные функции.
Уравнение (27.31) называется однородным, если f(x)=0.
Задачей Коши называется задача решения уравнения (27.31) при заданных начальных условиях 
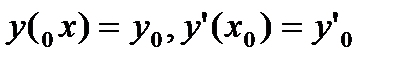 . Линейными независимыми решениями однородного уравнения
. Линейными независимыми решениями однородного уравнения
называется решение 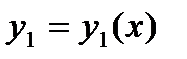 ,
, 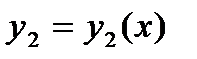 , для которого
, для которого
определитель Вронского (вронскиан)
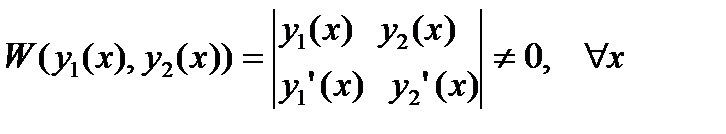 , (27.32)
, (27.32)
И линейно зависимыми, если 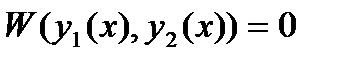 для некоторых х. Известно, что всякое линейное уравнение однородное уравнение
для некоторых х. Известно, что всякое линейное уравнение однородное уравнение
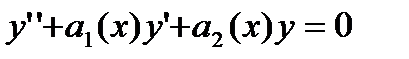 , (27.33)
, (27.33)
где 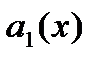 и
и 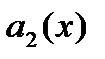 - непрерывные функции, имеет два линейно
- непрерывные функции, имеет два линейно
независимых решения. Фундаментальной системой решений называется система двух линейно независимых функций 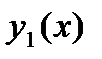 и
и 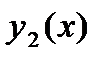 , являющихся решениями однородного уравнения (27.33). Для решений уравнений вида (27.31) применяется метод вариации произвольных постоянных, который заключатся в том, что общее решения уравнения (27.31) ищется в виде
, являющихся решениями однородного уравнения (27.33). Для решений уравнений вида (27.31) применяется метод вариации произвольных постоянных, который заключатся в том, что общее решения уравнения (27.31) ищется в виде
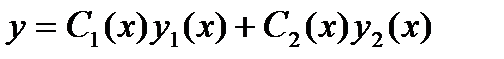 , (27.34)
, (27.34)
где 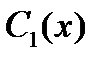 и
и 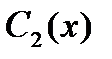 -функции, которые определяются из
-функции, которые определяются из
системы уравнений
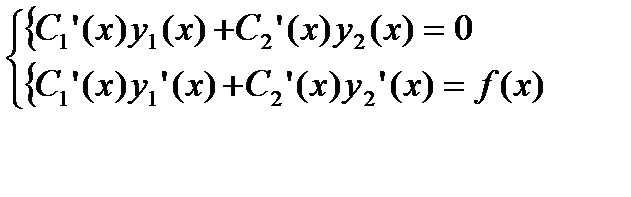 . (27.35)
. (27.35)
Из системы (27.35) находится
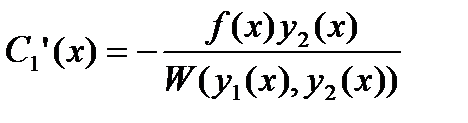 ,
, 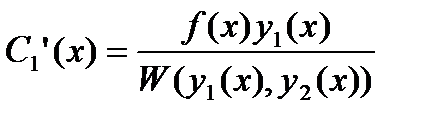 (27.36)
(27.36)
Тогда
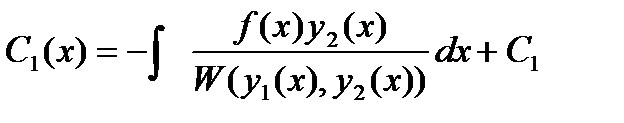 (27.37)
(27.37)
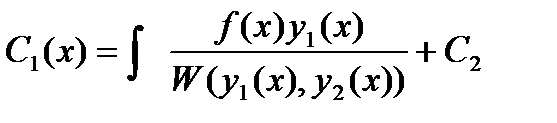
Дата: 2016-10-02, просмотров: 326.