Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Периодические функции

Функция f(x) называется периодической, если существует постоянное число Т>0, для которого f(x+T)=f(x); каково бы ни было х из области задания этой функции (подразумевается, что в область задания вместе с х входят х+Т и х-Т ). Число Т с таким свойством называется периодом функции f(x). Наиболее известными периодическими функциями являются sin x, cos x, tg x … с периодическими функциями приходится иметь дело во многих приложениях математики к задачам физики и техники.

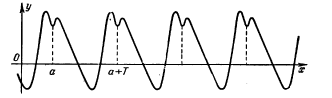
Рис. 31.1.

Сумма, разность произведение и частное функций периода Т, очевидно, всегда дают функции того же периода.

Если мы построим график периодической функции у(х) для какого-нибудь отрезка [a,a+T] значений х, то полный график этой функции получим периодическим повторением построенного (рис. 31.1 ).

Если Т есть период функции f(x), то числа 2Т, 3Т, 4Т,…будут так же периодами, что сразу вытекает из рассмотрения графика периодической функции или из цепи равенств

f(x)=f(x+T)=f(x+2T)=f(x+3T)=… (31.1)

(Наряду с этим равенством справедливы и такие :

f(x)=f(x-T)=f(x-2T)=f(x-3T)=….) являющиеся следствием многократного пользования условием (1.1). Таким образом, если Т-период, то и всякое число вида kT, где k-целое положительное число, есть также период, т. е. период, если он существует, всегда не единственен. Отметим следующее свойство любой функции f(x) периода Т.

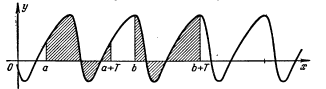
Рис. 31.2

Если функция f(x) интегрируема на некотором отрезке длины Т, то она интегрируема на всяком другом отрезке той же длины, и величина интеграла при этом неизменна, т.е.

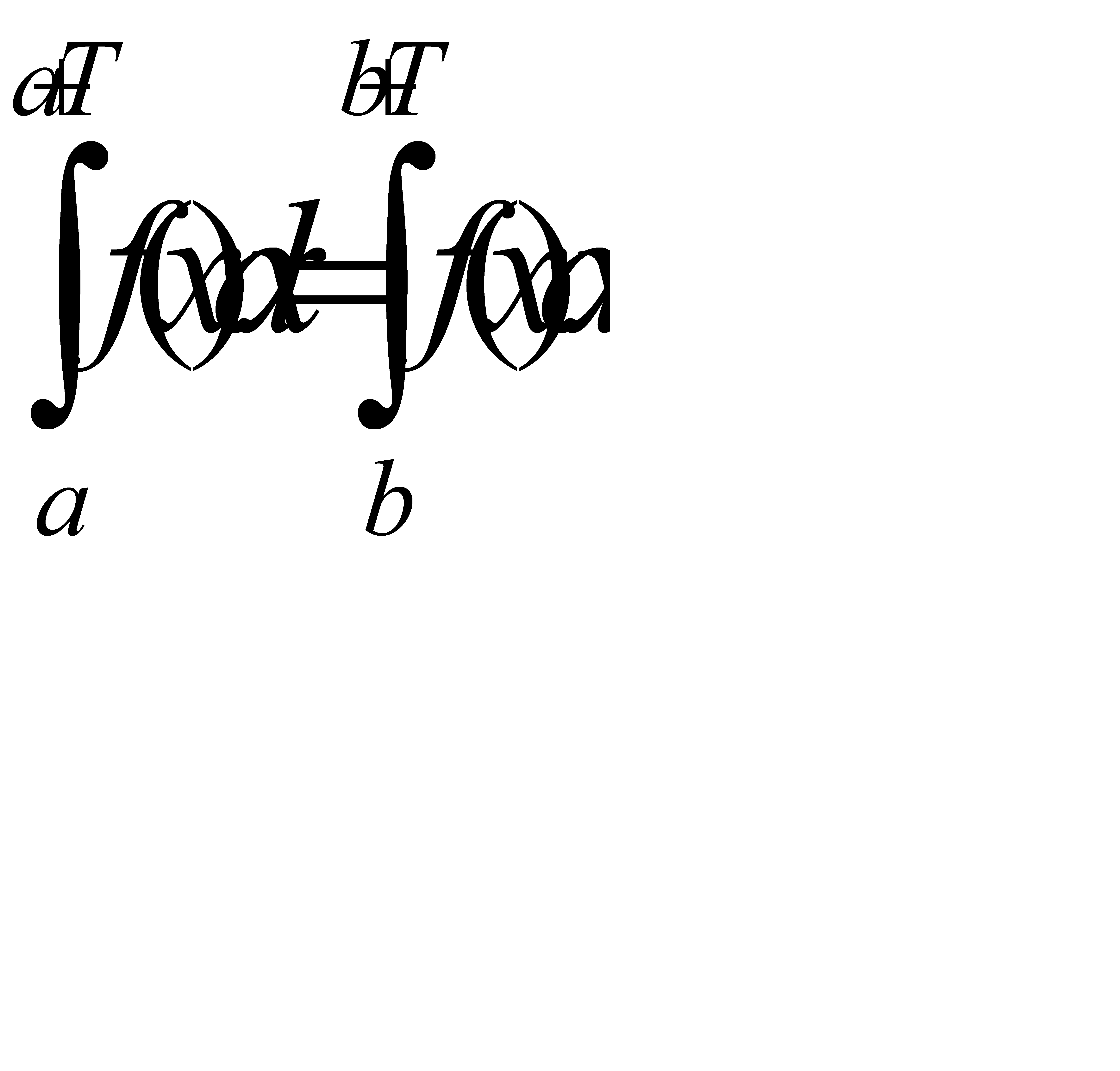(31.2)

при любых а и b.Это свойство легко вытекает из интерпретации интеграла как площади. Действительно, интеграл слагается из площадей, заключенных между кривой y= f(x), крайними ординатами и осью Ох, причем площади, лежащие над осью Ох, со знаком «+», а лежащие под осью Ох, со знаком «-». В нашем случае в силу периодичности f(x) эти площади оказываются одинаковыми для обоих интегралов (31.2) (рис.31.2).

В дальнейшем, когда мы будем говорить, что функция периода Т интегрируема, то будем под этим подразумевать ее интегрируемость на отрезке длины Т, а значит, и на любом отрезке конечной длины, как это легко следует из только что установленного свойства.

Гармоники

Простейшей, и в то же время очень важной для приложений, является периодическая функция 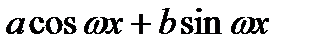, где А, a,b, 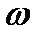, 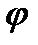- постоянные. Эту функцию называют гармоникой с амплитудой |А|, частотой 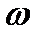и начальной фазой 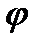. Гармоника имеет период Т=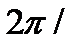 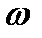. Действительно, при любом х

 

.

 

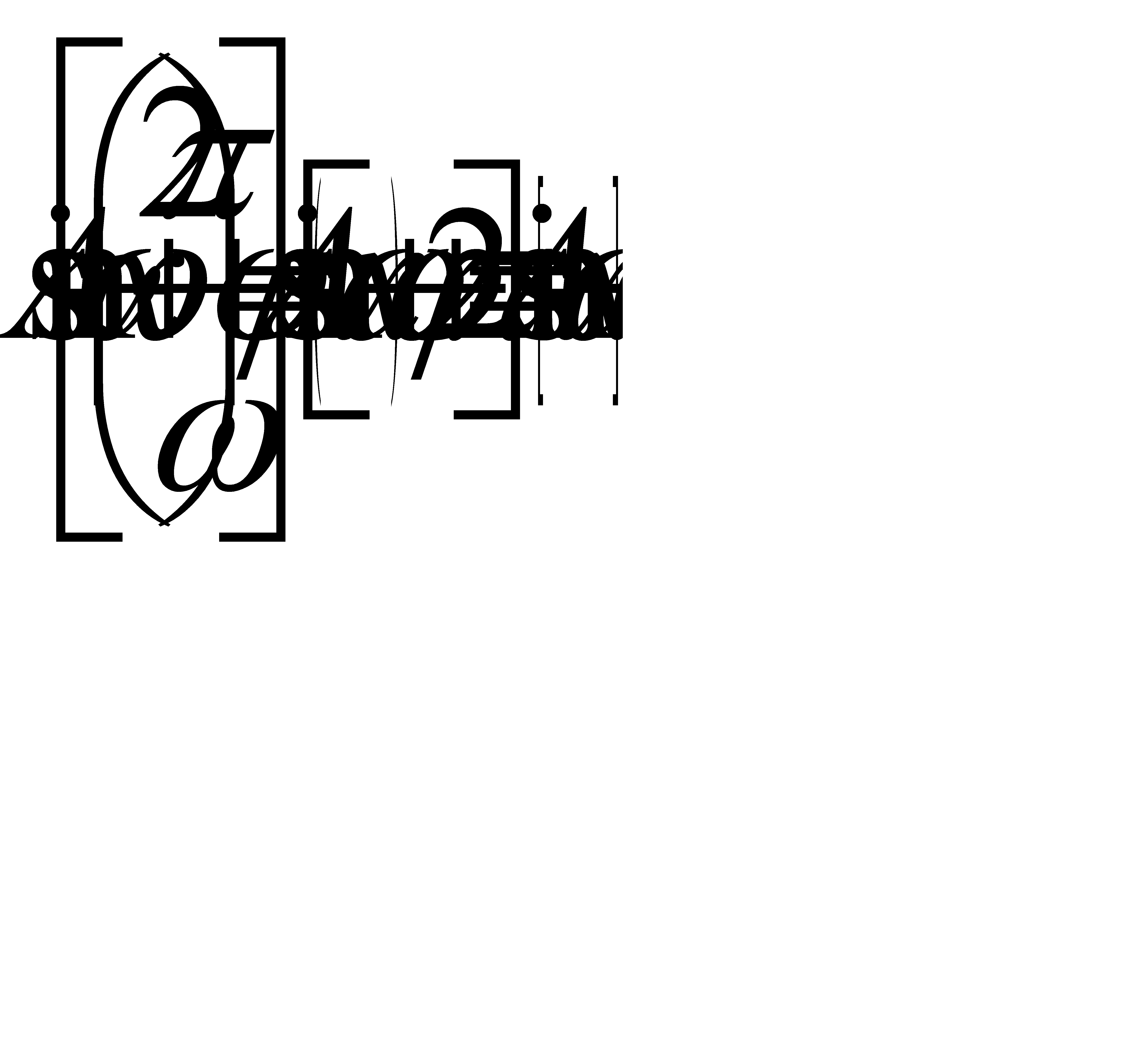Рис. 31.3

 

Происхождение наименований «амплитуда», «частота», «начальная фаза» связано с задачей механики о гармонических колебаниях. Пусть материальная точка М с массой m движется по прямой под действием силы F, пропорциональной расстоянию s точки М от фиксированной точки О (рис. 31.3). Считая, s>0 справа от О и s<0 слева от О, находим F=-ks, где k-коэффициент пропорциональности, k>0. Имеем 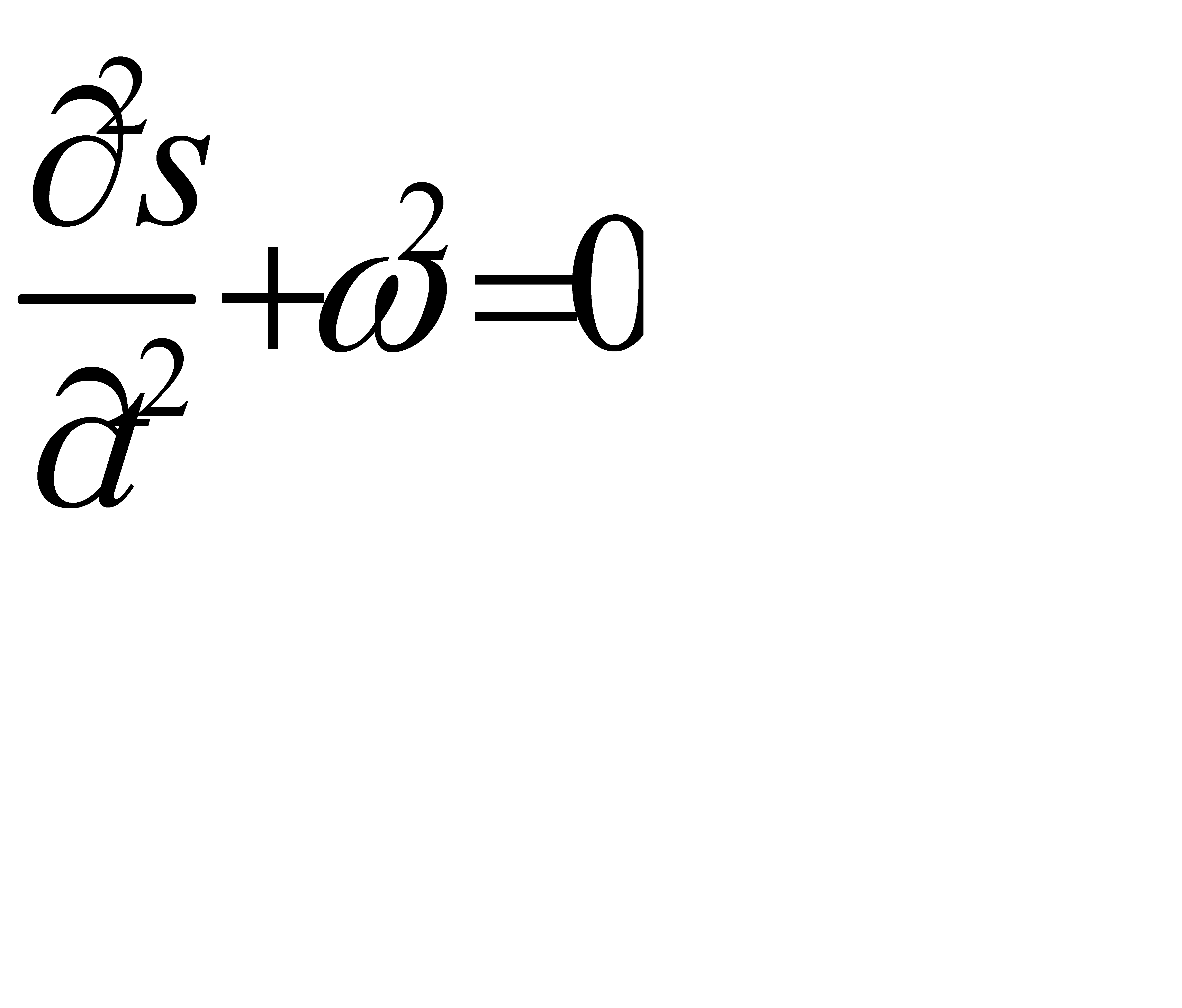, где положено 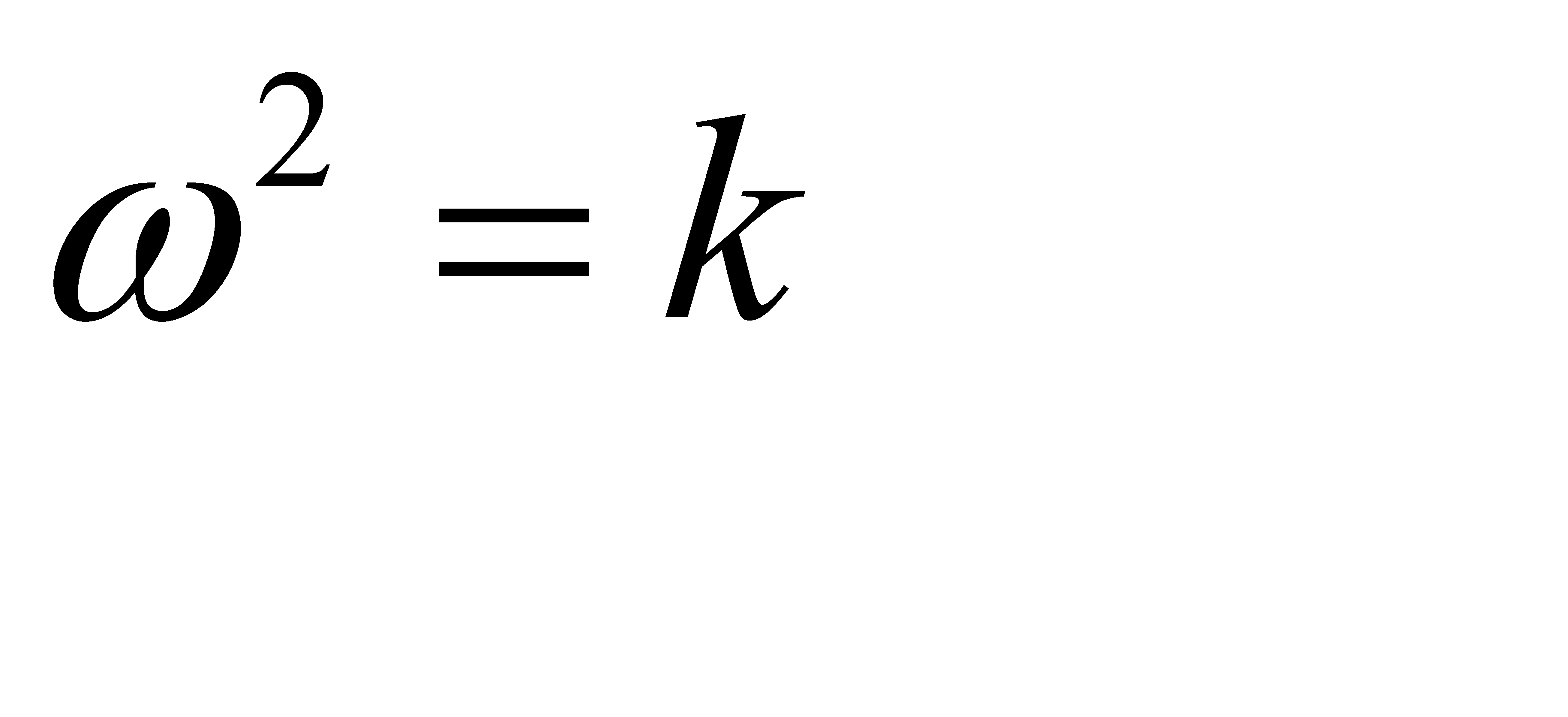/m, откуда .

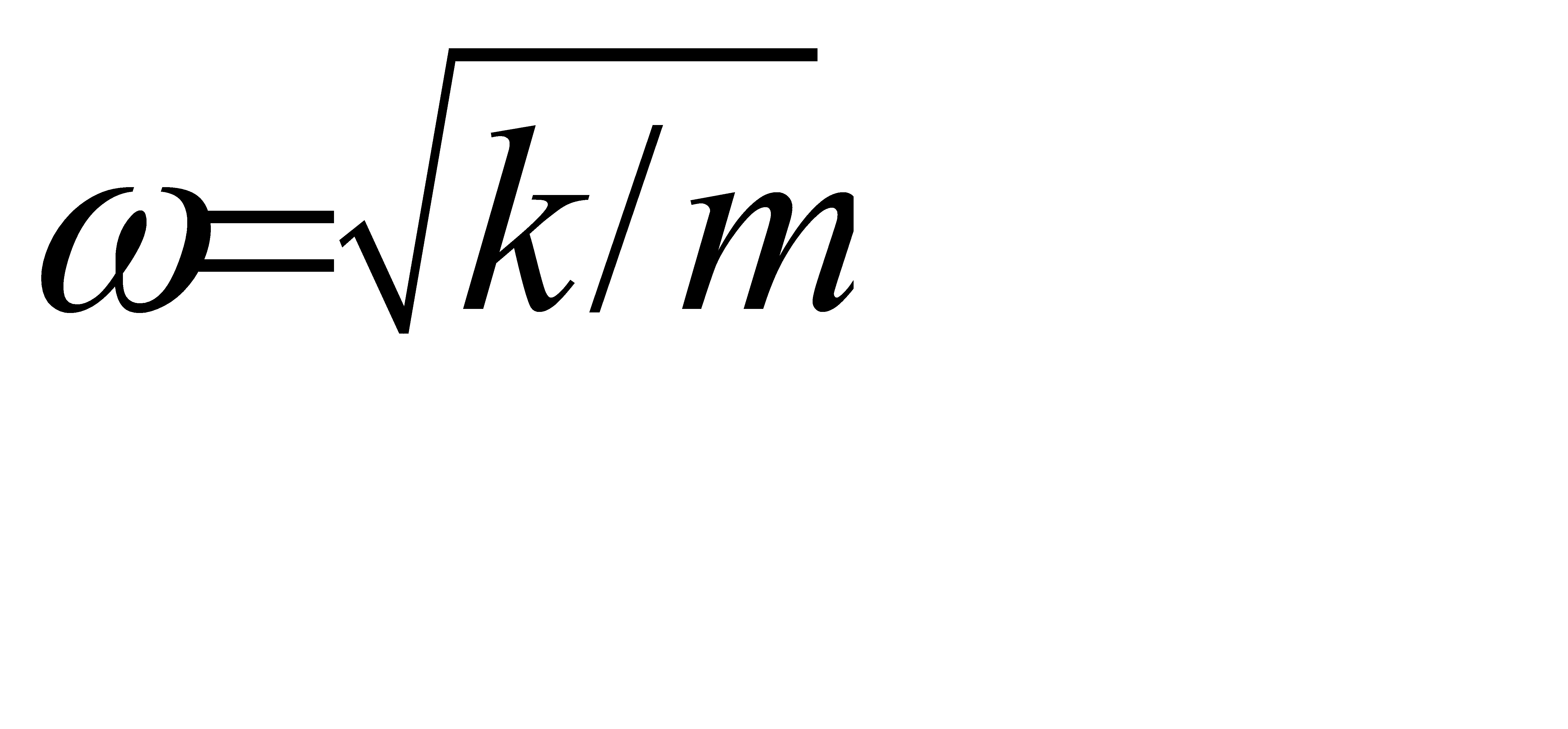Решением полученного уравнения будет функция 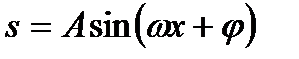, где А и 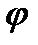- постоянные, которые вычисляются, зная положение и скорость точки М в начальный момент. Таким образом, s есть периодическая функция времени t с периодом Т= .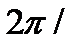

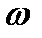Это означает, что точка M будет совершать колебательное движение. Амплитуда |A| есть максимальное отклонение точки М от О. Величина 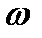= 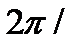T - число колебаний за отрезок времени .

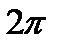Рис. 31.4

Отсюда наименование «частота». Величина -начальная фаза- характеризует положение точки М в начальный момент, так как при t=0 имеем: . Возвратимся к гармонике 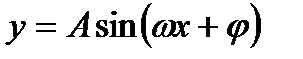. Как выглядит её график. Будем считать 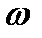>0, так как в противном случае знак минус мы могли бы вынести из-под знака sin. В наиболее простом случае- при А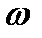=1, =1, 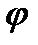=0- мы получаем функцию y=sinx, т.е. обычную синусоиду (рис. 31.4,а). при А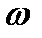=1, =1, 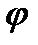= 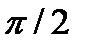мы получаем косинусоиду y=cosx, график которой есть сдвинутый на 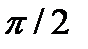влево от графика синусоиды y=sinx.

Рассмотрим гармонику y=sin 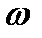x и положим 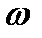x=z. Получим y=sinz. Мы пришли к обычной синусоиде. Но x=z/ 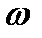. Следовательно, график гармоники y=sin 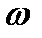x можно получить из графика обычной синусоиды с помощью деформации последнего в направлении оси абсцисс. При 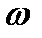>1 деформация сводится к равномерному сжатию в 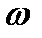раз, а при 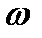<1 к растяжению в 1/ 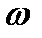раз. На рис.31.4,б изображена гармоника y=sin3x с периодом Т= 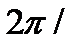3. Рассмотрим теперь гармонику 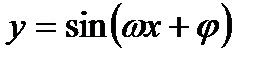и положим 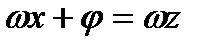. График гармоники 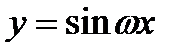нам уже известен. Но x=z- 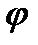/ 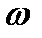. Следовательно, график гармоники 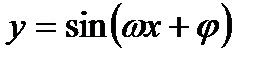получается из графика гармоники 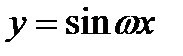сдвигом на - 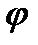/ 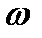вдоль оси абсцисс. На рис. 31.4,в изображена гармоника 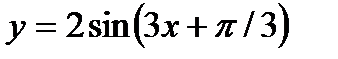с периодом Т=2 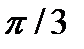и начальной фазой 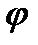= 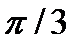. Наконец, график гармоники 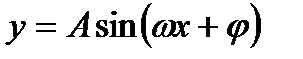получается из графика гармоники 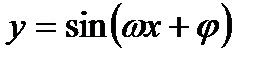умножением всех ординат на число А. на рис.31.4,г изображена гармоника .

Резюмируем сказанное: график всякой гармоники 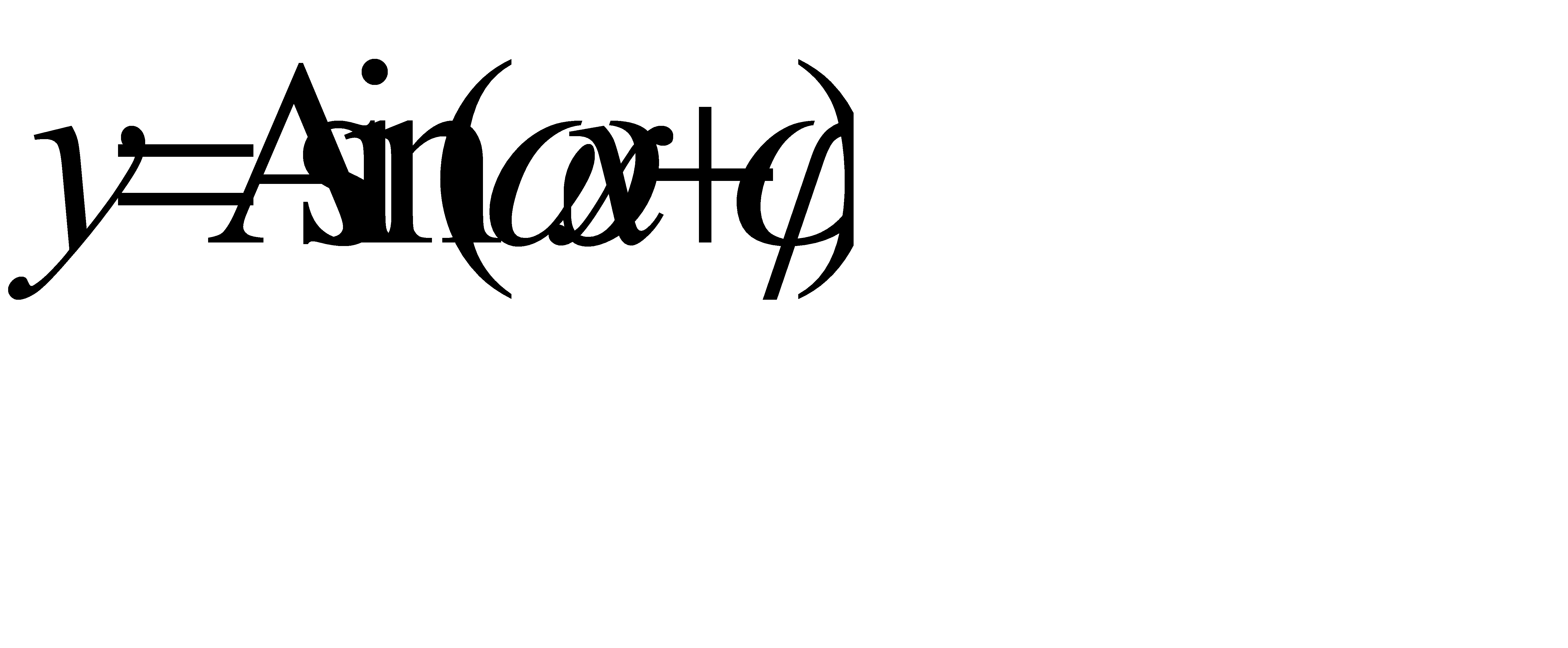получается из графика обычной синусоиды равномерным сжатием (или растяжением) в направлении осей координат и сдвигом вдоль оси Ох.

Пользуясь известной формулой тригонометрии, напишем:

.

Положив

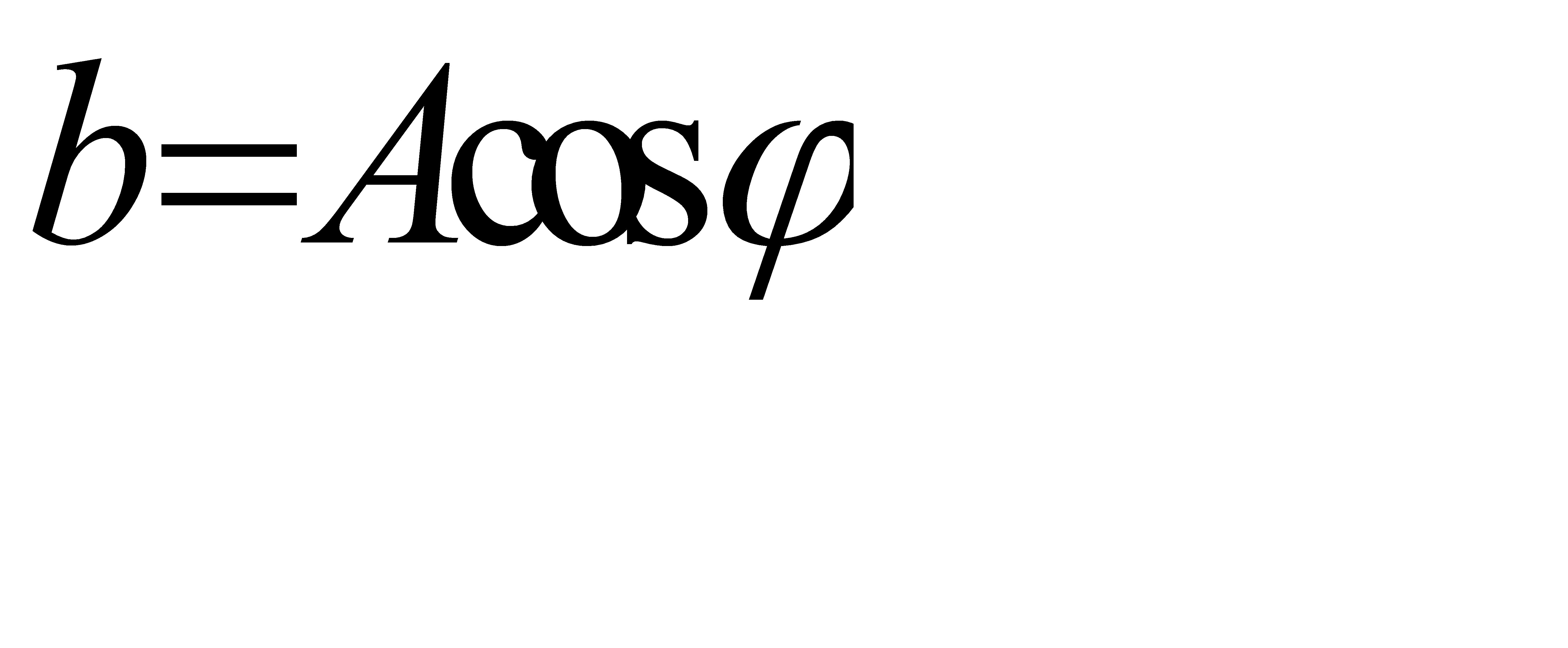, (31.3)

убедимся, что всякую гармонику можно представить в виде

(31.4)

Обратно, всякая функция вида (31.4) есть гармоника. Чтобы убедится в этом, достаточно найти А и из уравнений (31.3). При этом получим:

, , ,

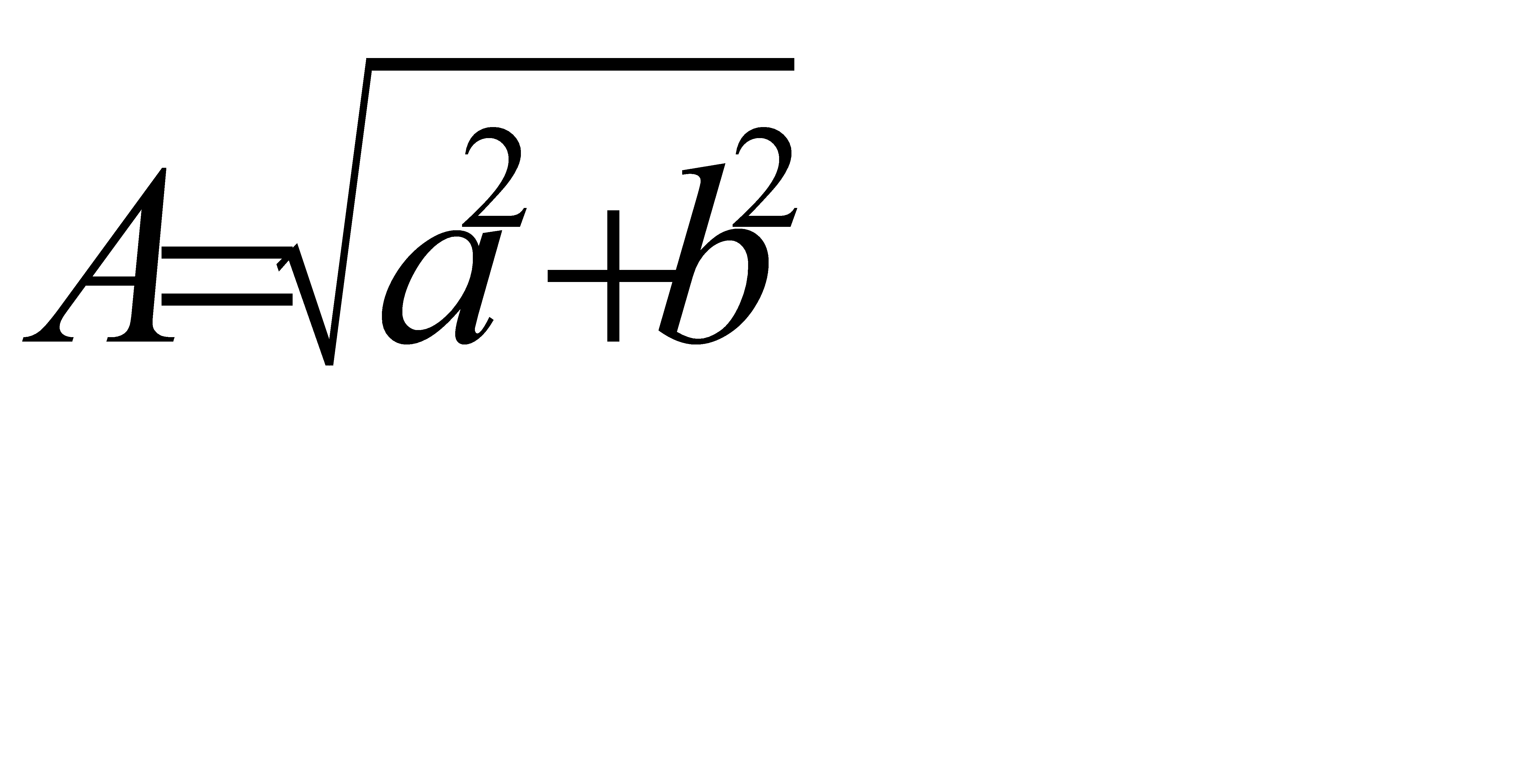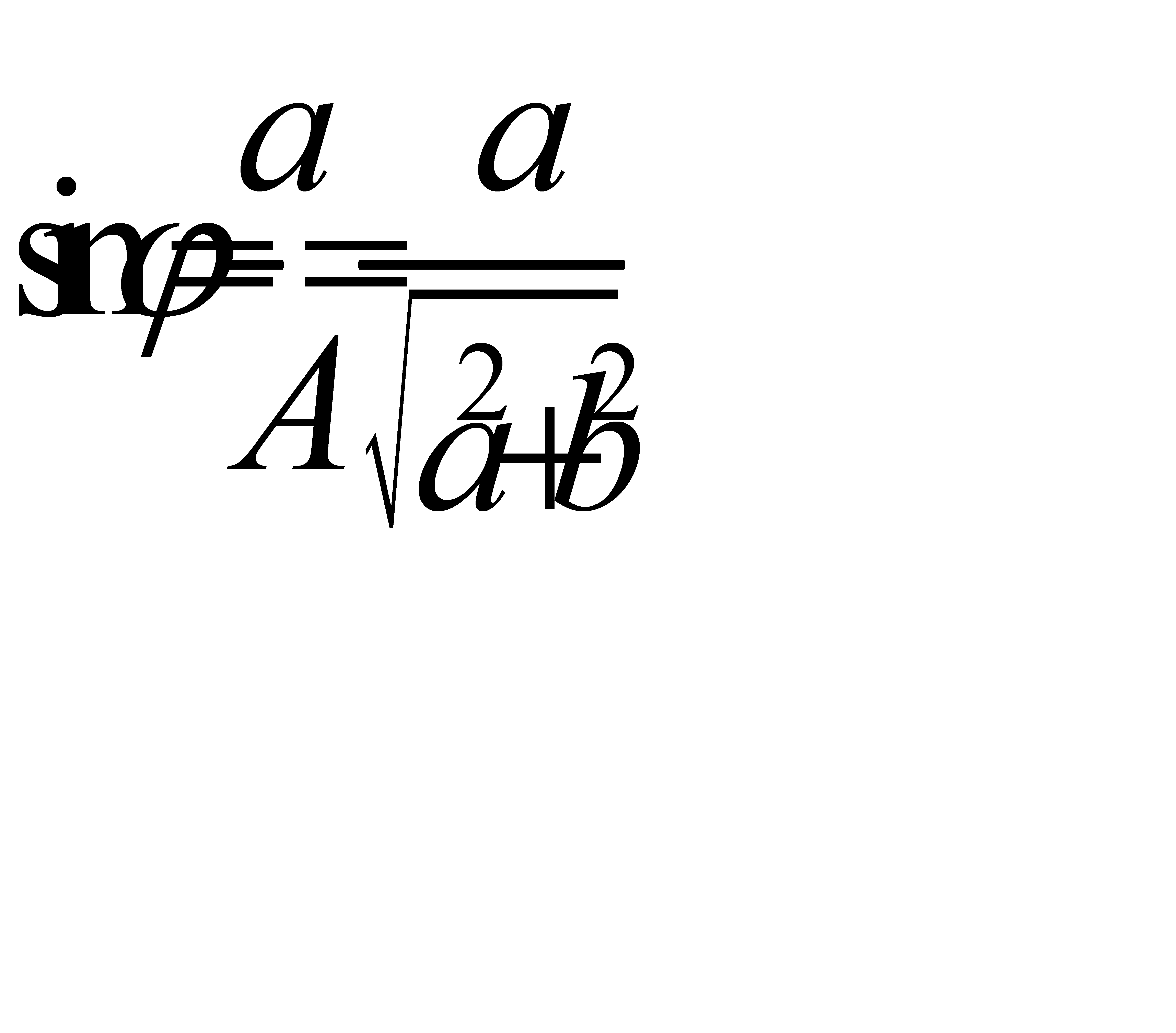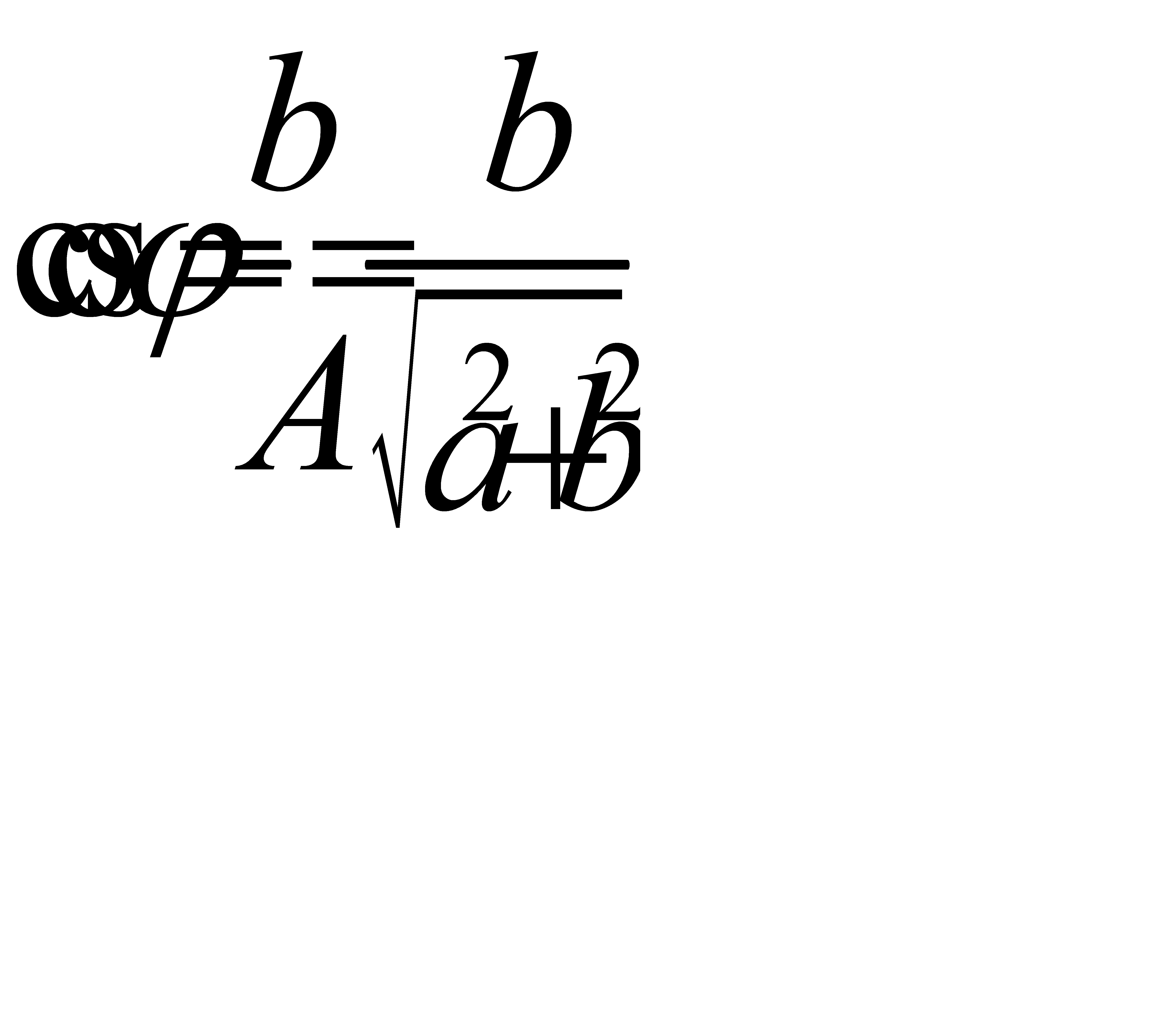откуда 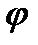легко находится. В дальнейшем для гармоник мы будем пользоваться записью виды (31.4). Эта запись для гармоники 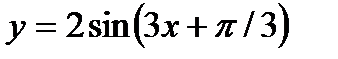, изображение на рис. 31.4,г, дает:

. Нам удобно будет также в (31.4) явно ввести период Т следующим образом: Положим Т=2l. Тогда вследствие равенства Т=2 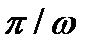получим:

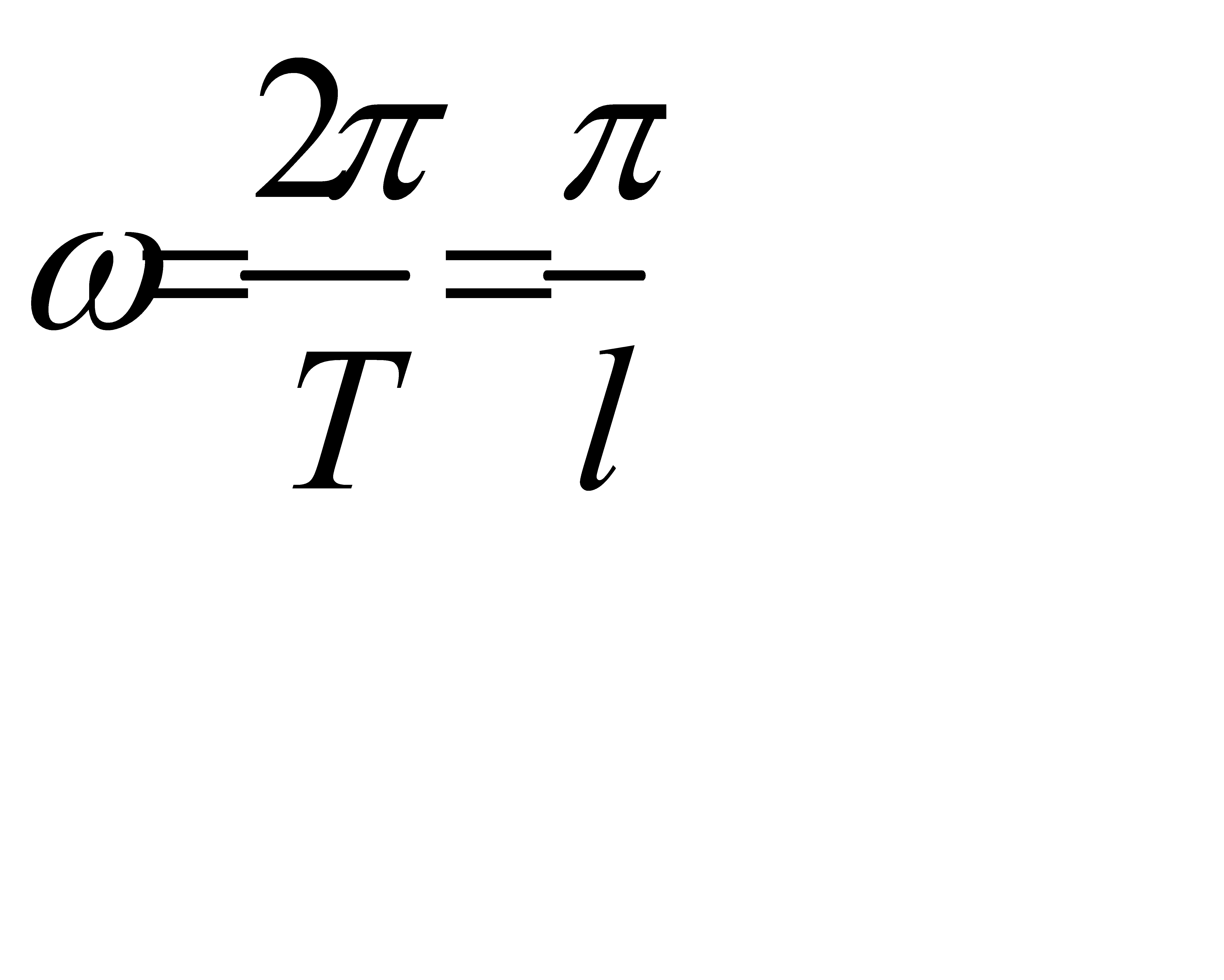и, следовательно, гармоника с периодом T=2l может быть записана так:

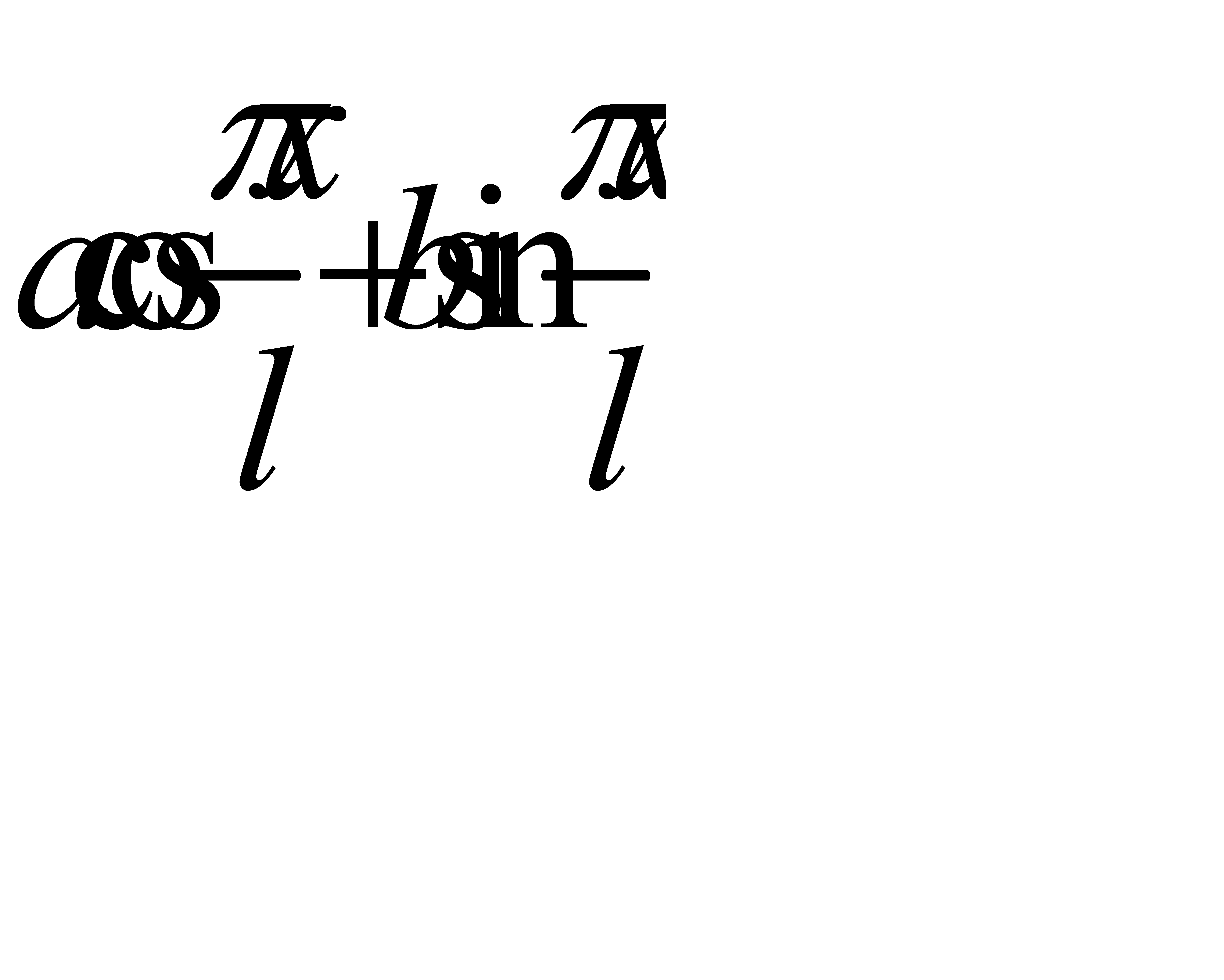(31.5)

Тригонометрические многочлены и ряды

Зададимся числом T=2l и рассмотрим гармонику

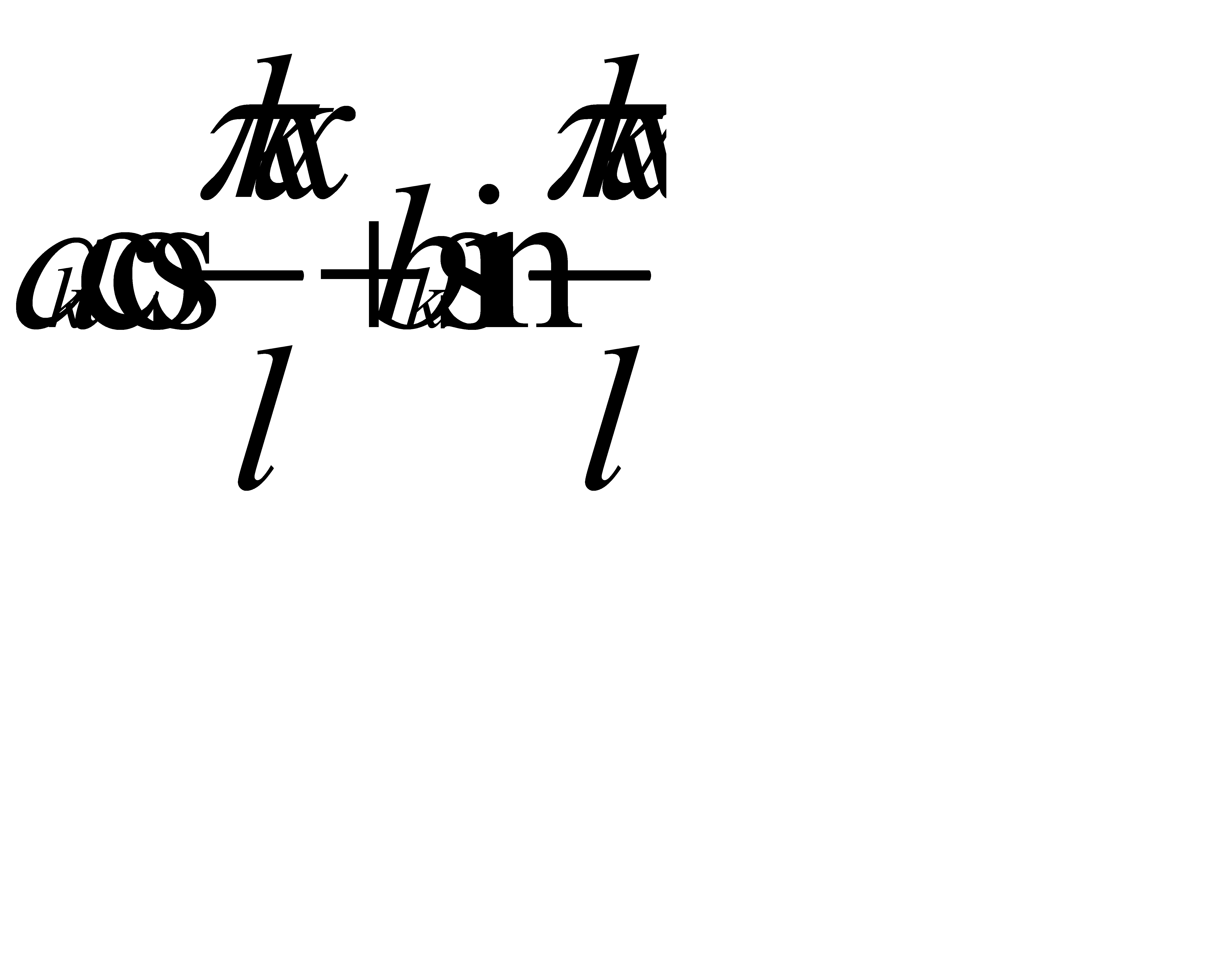(k=1, 2, ….) (31.6)

с частотами 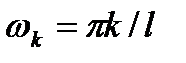и периодом 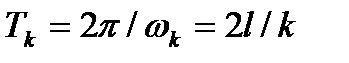. Поскольку 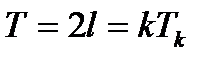, постольку число T=2l является периодом для всех гармоник (31.6) сразу. Всякая сумма вида

S_n(x)= ,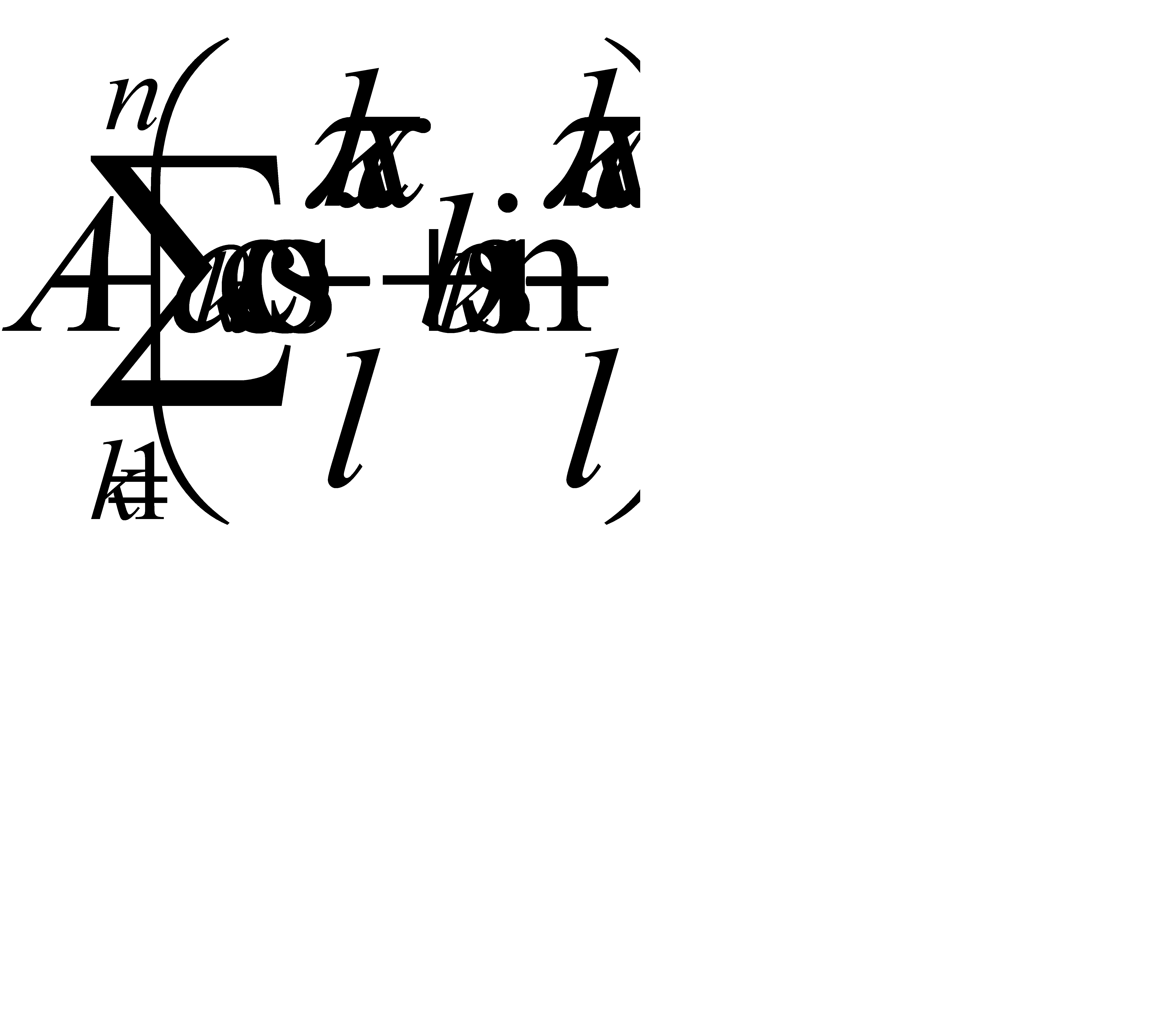

где A=const, будучи суммой функций периода 2l, есть функция того же периода (прибавление постоянной, очевидно не нарушает периодичности; к тому же постоянную можно рассматривать как функцию, для которой любое число является периодом ). Функцию S_n(x) будем называть тригонометрическим многочленом порядка n (периода 2l). Тригонометрический многочлен хотя и слагается из нескольких гармоник, но представляет собой вообще функцию значительно более сложной природы, нежели простая гармоника. Располагая значениями постоянных A, a₁, b₁, a₂, b₂,…, a_n, b_n, мы можем образовать функцию y=s_n(x) с графиками, совсем непохожими на плавный и симметричный график простой гармоники. На рис.31.5 изображен график тригонометрического многочлена

 

 

Рис. 31.5

Сумма бесконечного тригонометрического ряда

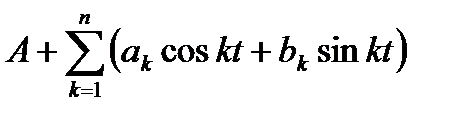
(если он сходится) представляет собой также функцию периода 2l. Природа функций, являющихся суммами таких тригонометрических рядов, ещё более разнообразна. Поэтому естественен вопрос: нельзя ли всякую заданную функцию периода T=2l представить в виде суммы тригонометрического ряда? Мы увидим, что такое представление действительно возможно для весьма широкого класса функций. Пусть f(x) принадлежит этому классу. Это значит, что f(x) может быть разложена в сумму гармоник, т.е. в сумму функций очень простой структуры. График функции y=f(x) получается «наложением» графиков гармоник. Если трактовать каждую гармонику как простое гармоническое колебание, а f(x) как характеристику сложного колебательного движения, то последнее оказывается разложенным на сумму отдельных гармонических колебаний. Не нужно, однако, думать, что тригонометрические ряды приложимы лишь к колебательным явлениям. Понятие тригонометрического ряда оказывается очень полезным и при изучении многих явлений совсем иной природы. Если

, (31.7)

то, положив 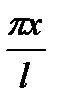=t или x= 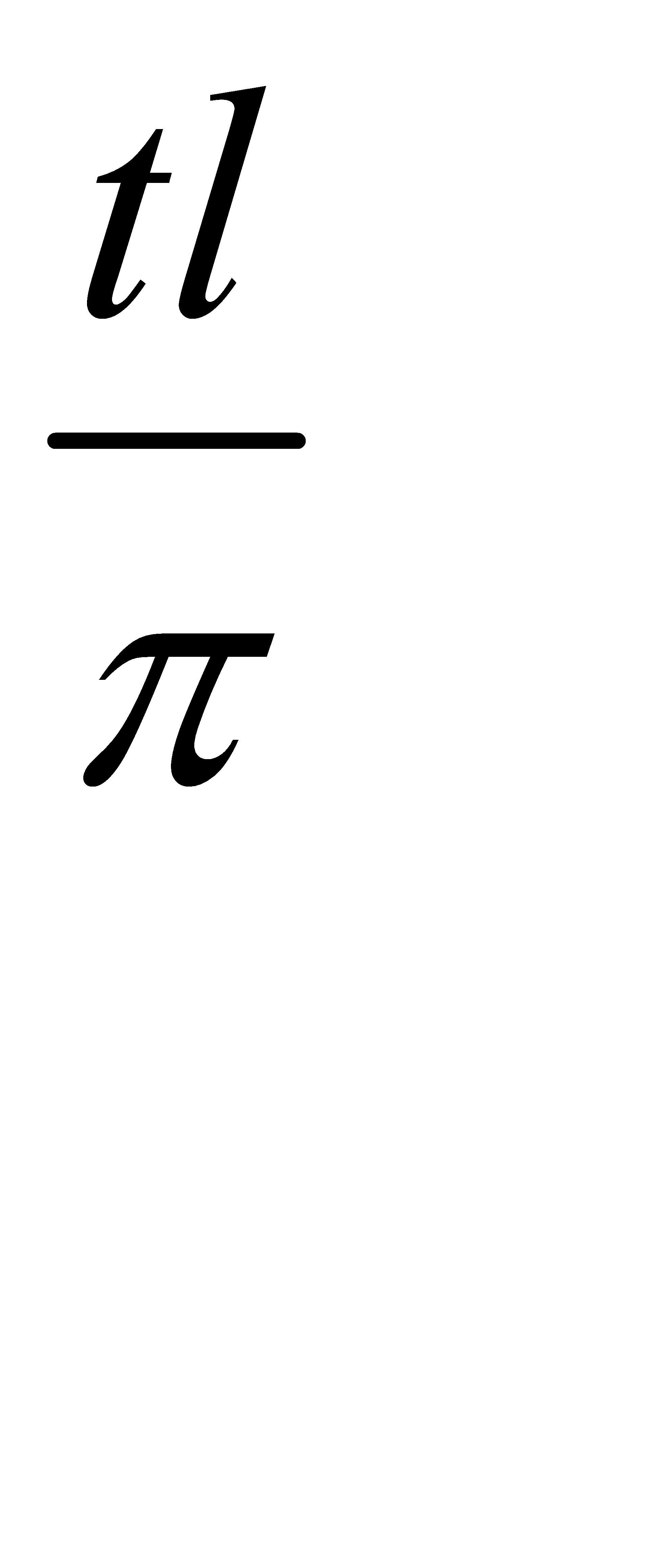, найдем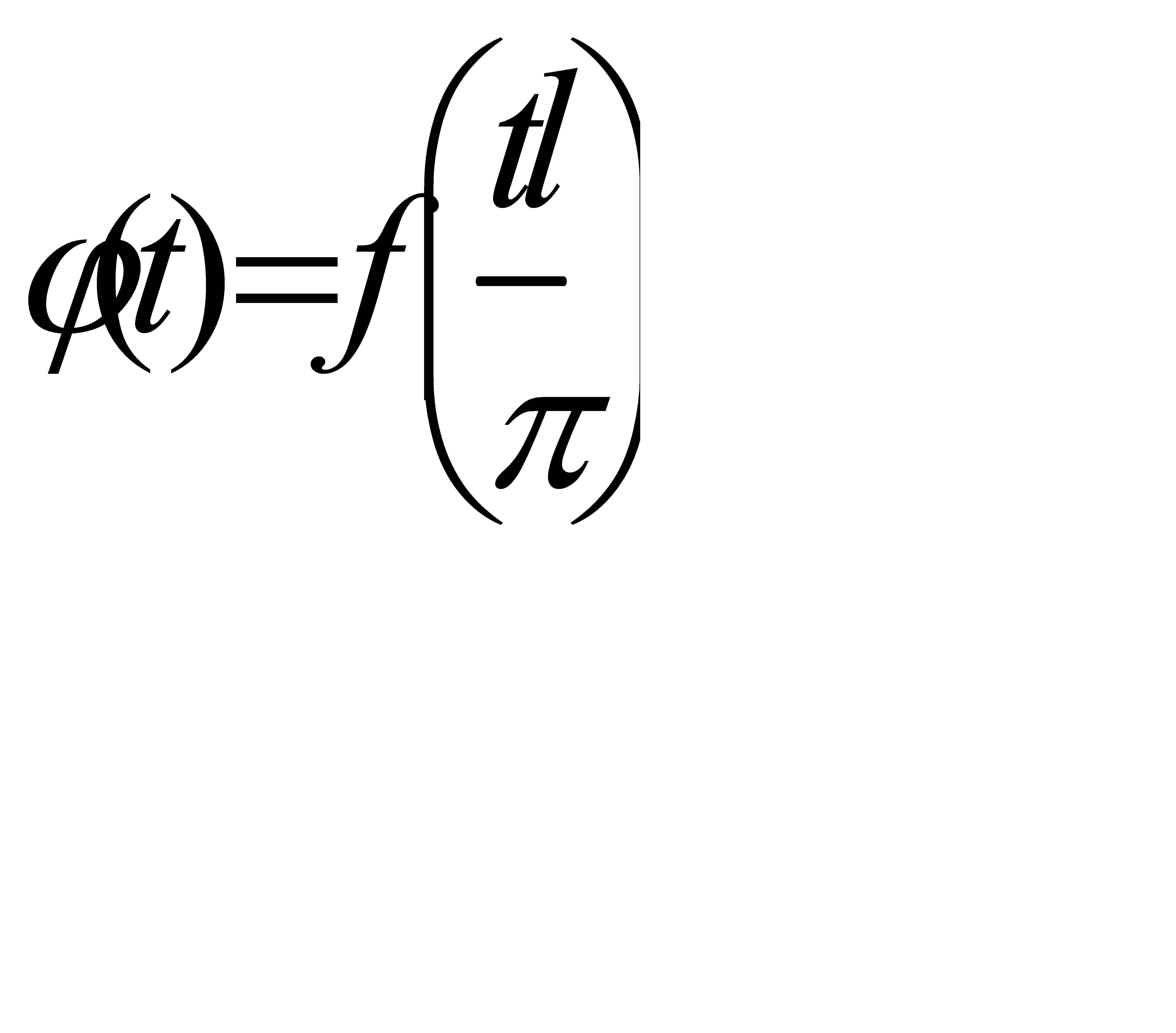

(31.8)

Гармоники этого ряда имеют общий период 2π. Таким образом, если для f(x) периода 2l имеет место разложение (31.7), то для функции 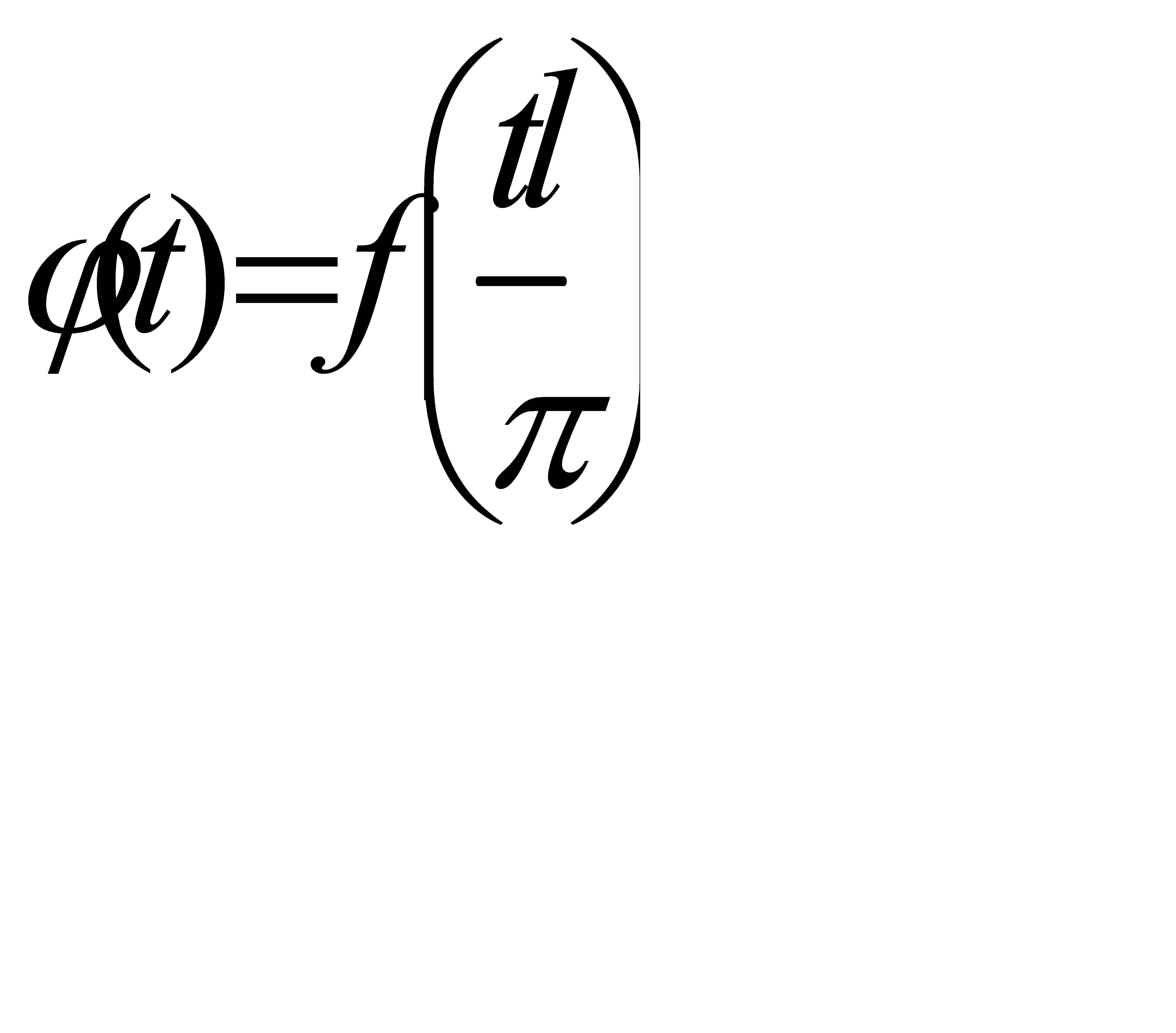периода 2π имеет место разложение (31.8). Справедливо, очевидно, и обратное заключение. Именно, если для функции φ(t) периода 2π имеет место разложение (31.8), то для функции 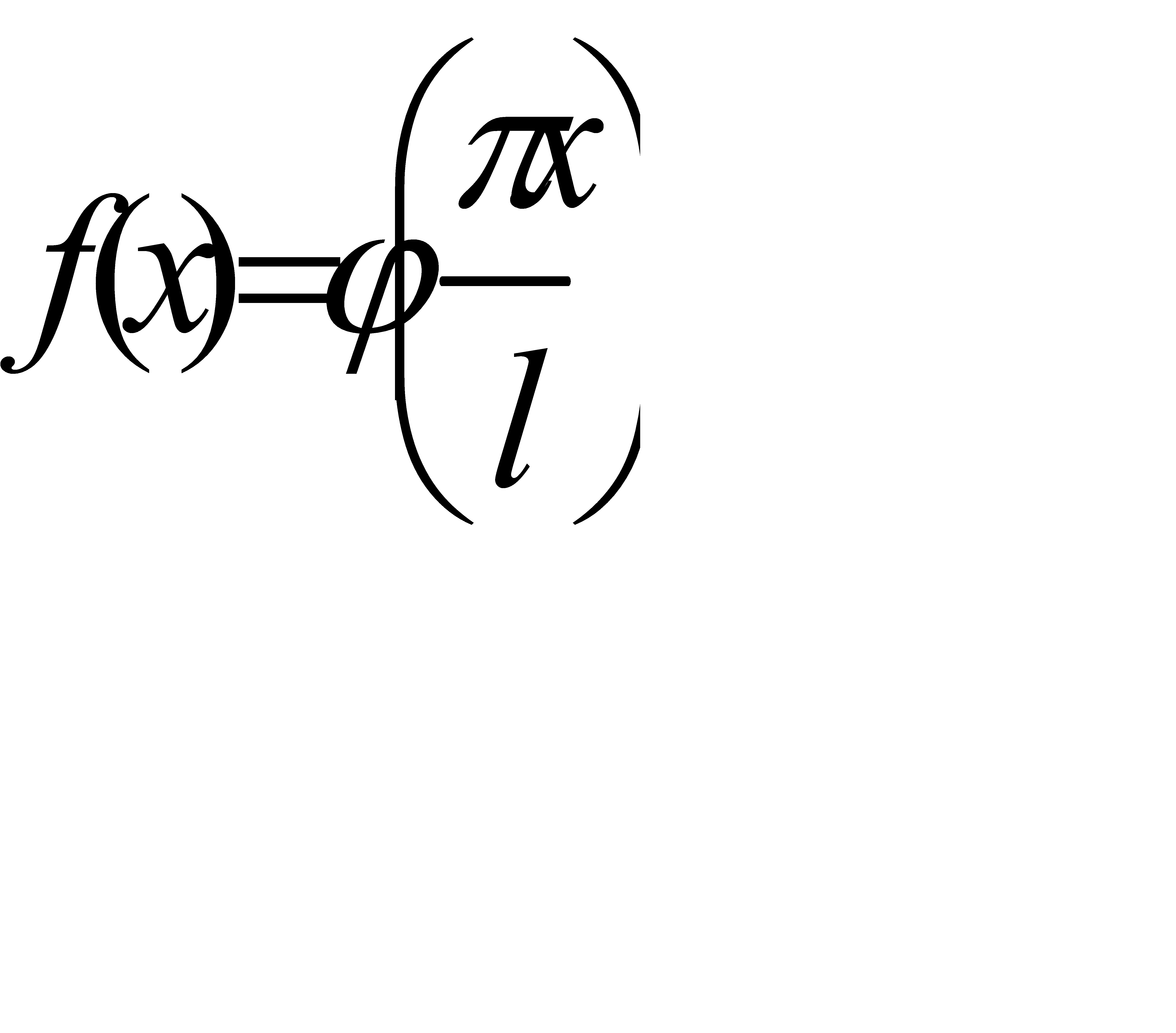периода 2l имеет место разложение (31.7).Таким образом, достаточно уметь решать задачу разложения в тригонометрический ряд для функций «стандартного» периода 2π. В этом случае к тому же и ряд выглядит проще. Поэтому мы и будем строить теорию для рядов вида (31.8) и лишь окончательные результаты будем переводить на «язык» общих рядов (31.7).

Уточнение терминологии. Интегрируемость.

Функциональные ряды

Уточним терминологию и напомним некоторые сведения из дифференциального и интегрального исчисления. Когда мы будем говорить, что f(x) интегрируема на отрезке [a,b], то будем иметь в виду существование интеграла

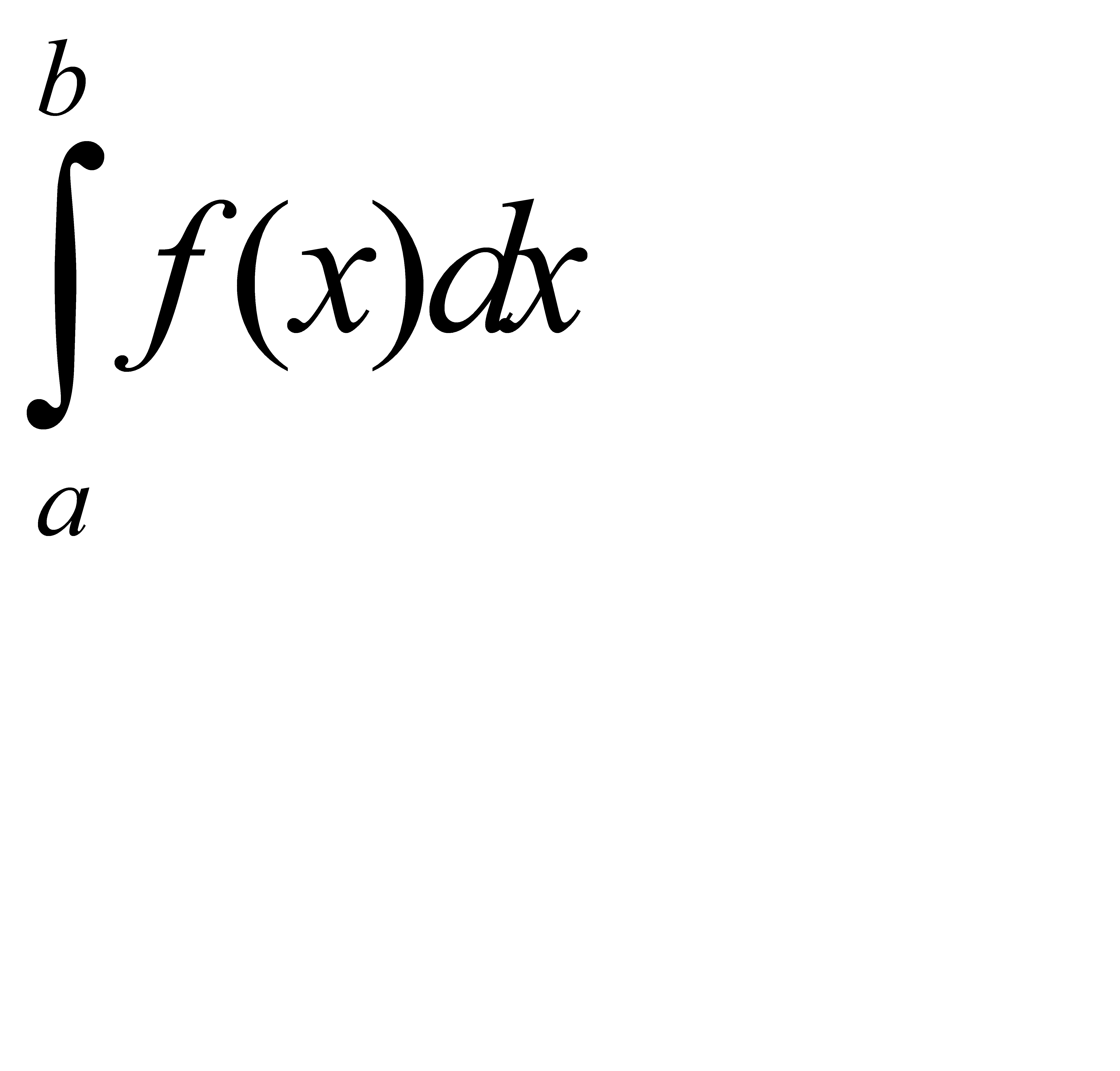(31.9)

Таким образом, интегрируемая f(x) у нас всегда либо непрерывна, либо имеет на отрезке [a,b] конечное число точек разрыва, вблизи которых функция может быть как ограниченной, так и неограниченной. В курсах интегрального исчисления доказывается, что для функции с конечным числом разрывов из существования интеграла 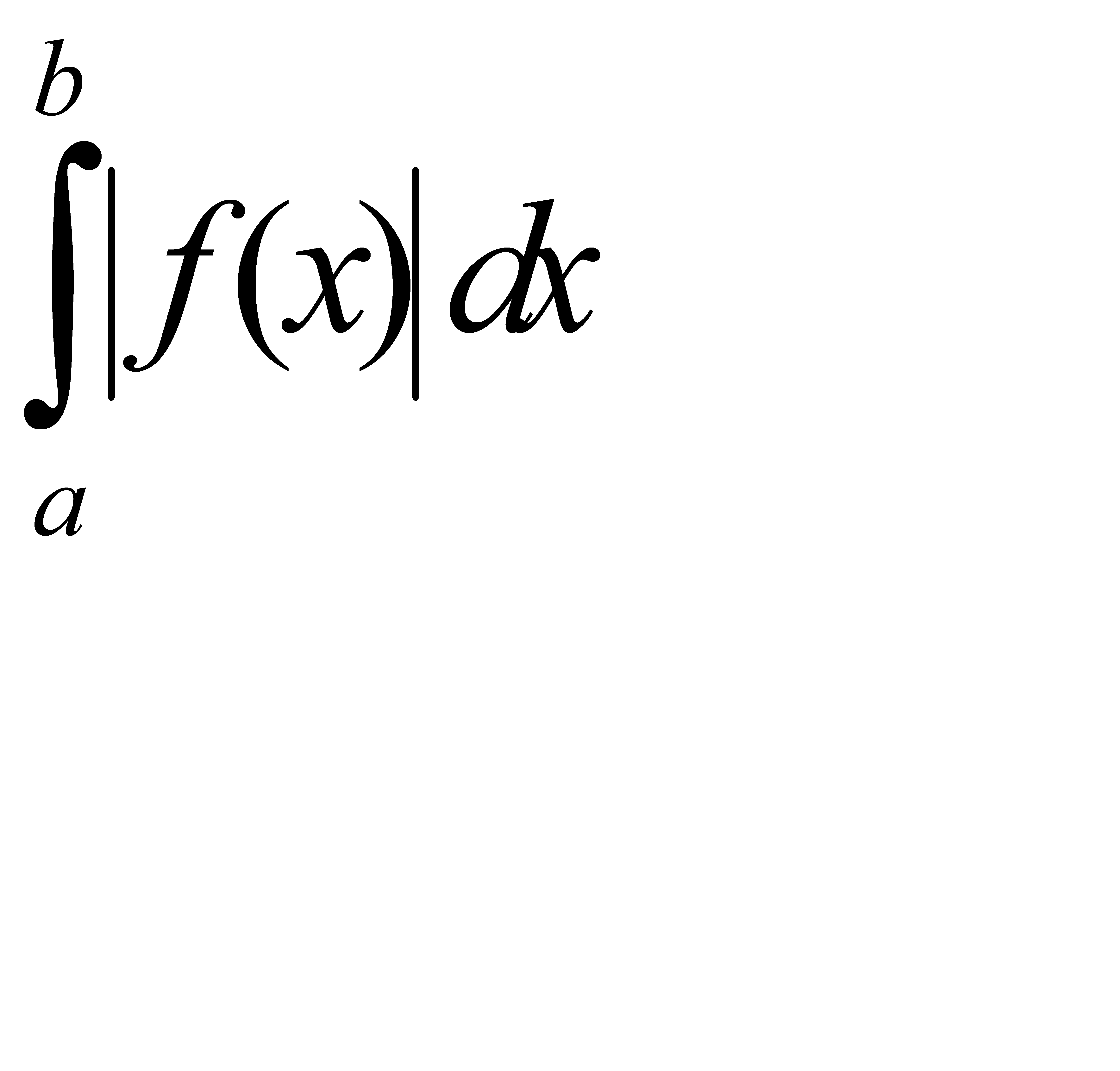всегда следует существование интеграла (31.9) (обратное не всегда верно). При этом функцию f(x) называют абсолютно интегрируемой. Если f(x) абсолютно интегрируема, а φ(x)-ограниченная интегрируемая функция, то произведение f(x)φ(x) абсолютно интегрируемо. 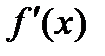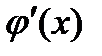Имеет место также следующее правило интегрирования по частям: Пусть f(x) и φ(x)-непрерывные на [a,b] функции, возможно лишенные производных в конечном числе точек, причем предполагается, что и абсолютно интегрируема. Тогда

(31.10)

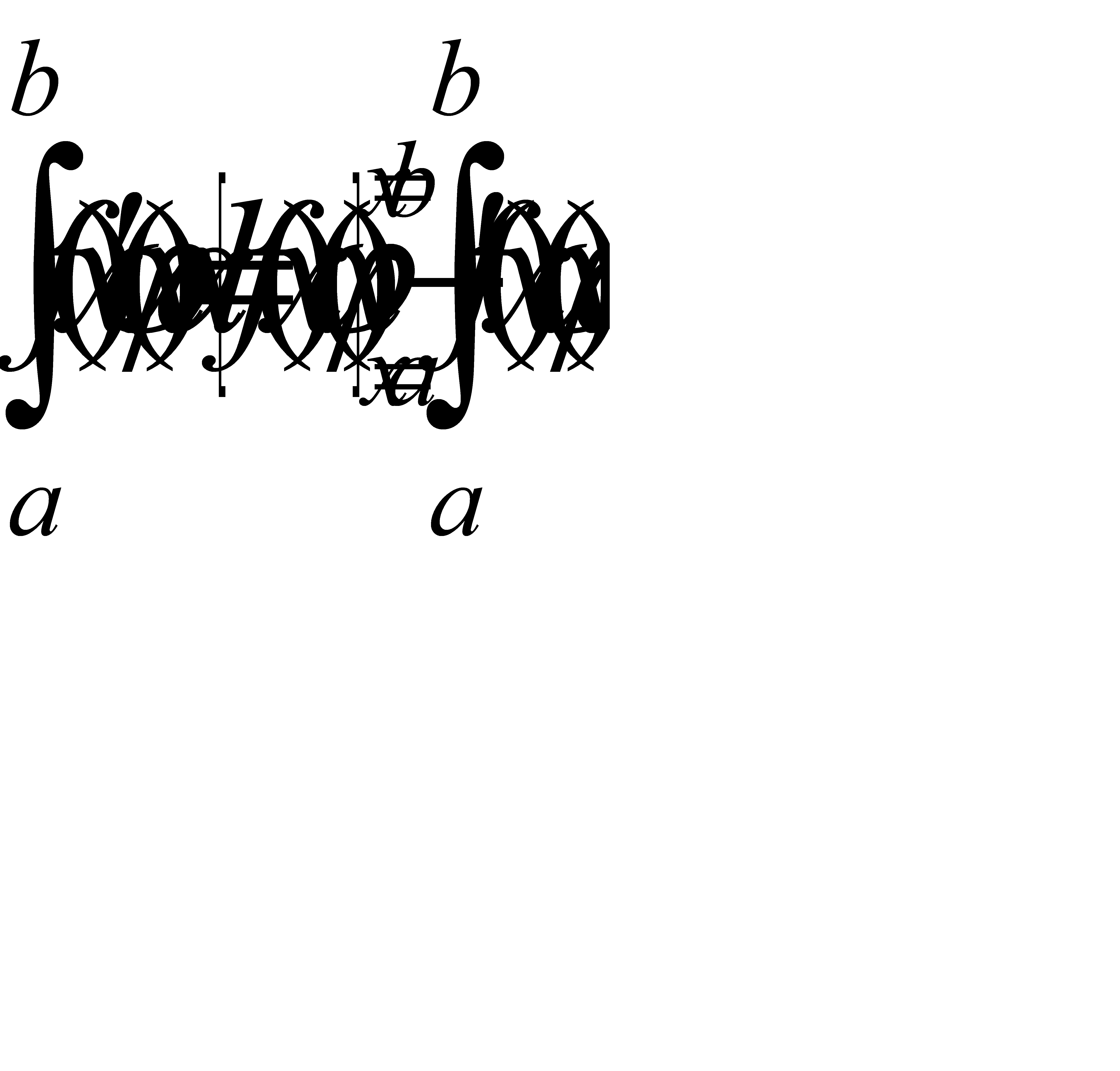
Известно: если функции f₁(x),f₂(x),…,f_n(x) интегрируемы на [a,b], то интегрируема и их сумма, причем

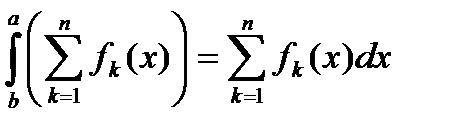(31.11)

Рассмотрим теперь бесконечный функциональный ряд

(31.12)

Он называется сходящимся для данного значения х, если для его частных сумм 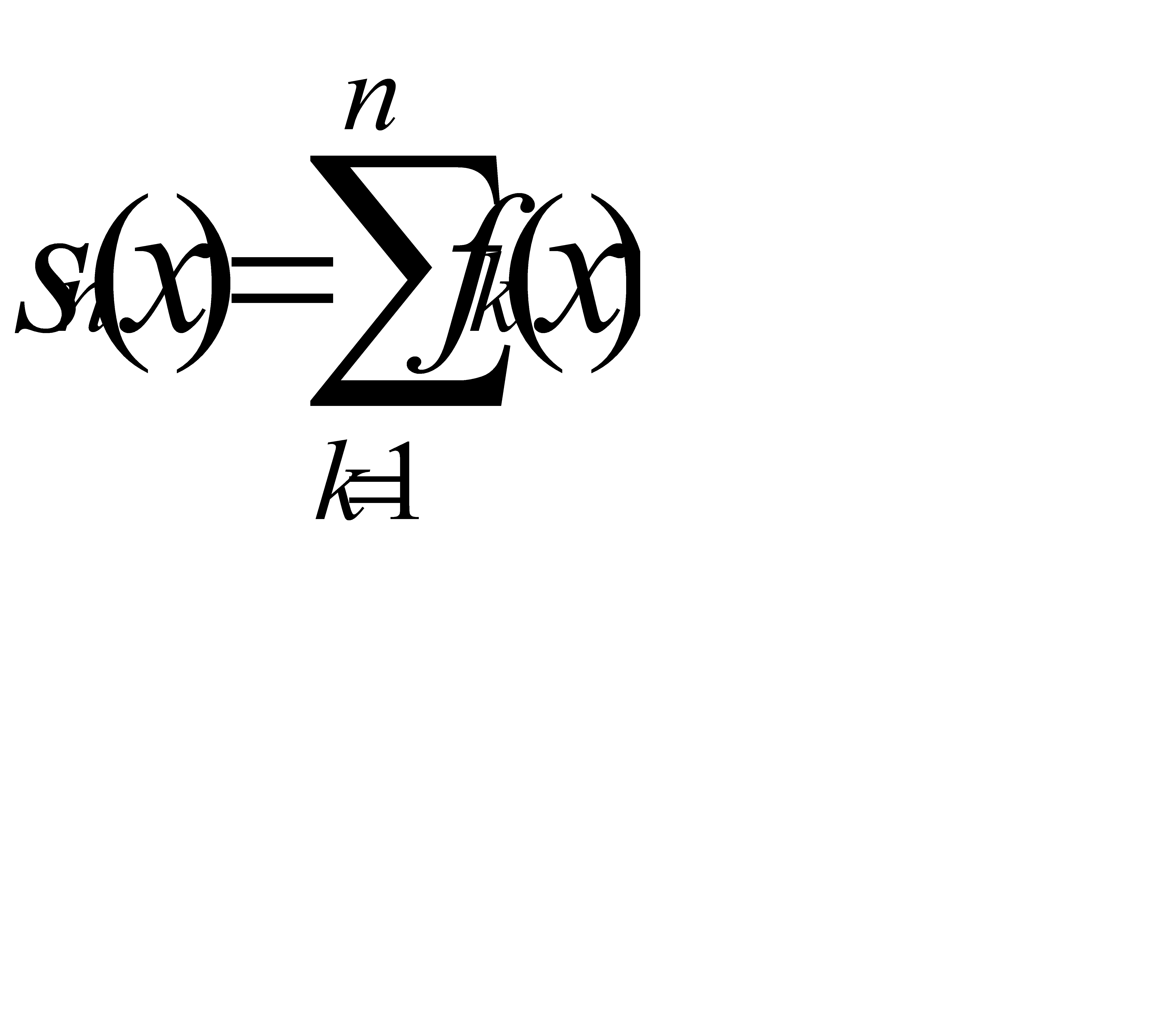(n=1, 2, … ) существует конечный предел . Величина s(x) называется тогда суммой ряда и, очевидно, представляет собой функцию от х. Если ряд сходится для всех х из отрезка [a,b], то его сумма s(x) определена на [a,b]. Распространяется ли формула (31.11) на случай сходящегося на отрезке [a,b] функционального ряда интегрируемых функций, т.е. справедлива ли формула

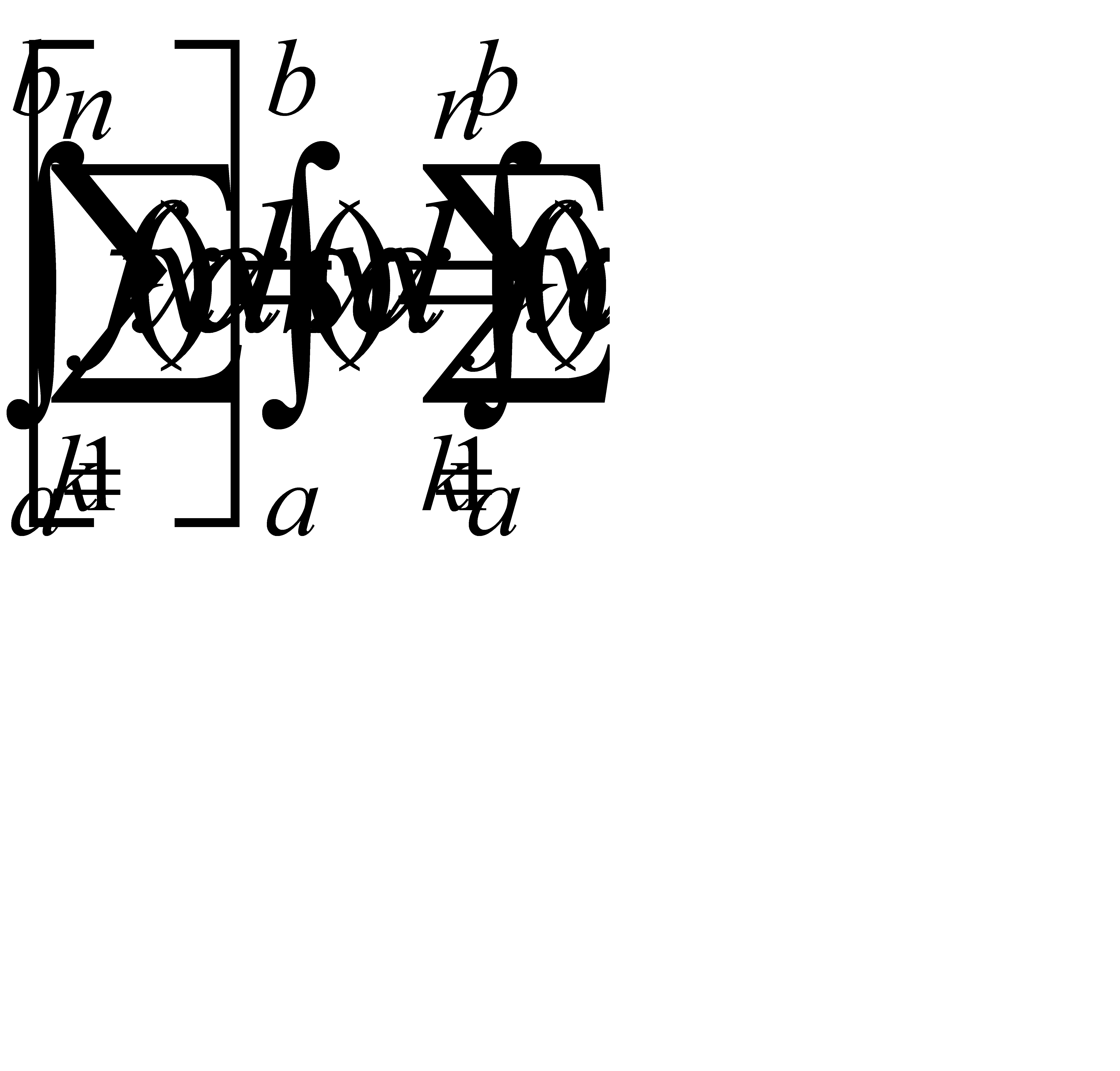(31.13)

(речь идет, таким образом, о возможности почленного интегрирования ряда)? Оказывается, что не всегда, и хотя бы уже потому, что ряд интегрируемых и даже просто непрерывных функций может иметь неинтегрируемую сумму. Аналогичная проблема связана с возможностью почленного дифференцирования рядов. Мы выделим важный класс функциональных рядов, к которым указанные операции приложимы. Говорят, что ряд (31.12) сходится равномерно на отрезке [a,b], если для всякого положительного числа ε существует число N такое, что для всех n≥N и для всех х из отрезка [a,b] выполняется неравенство

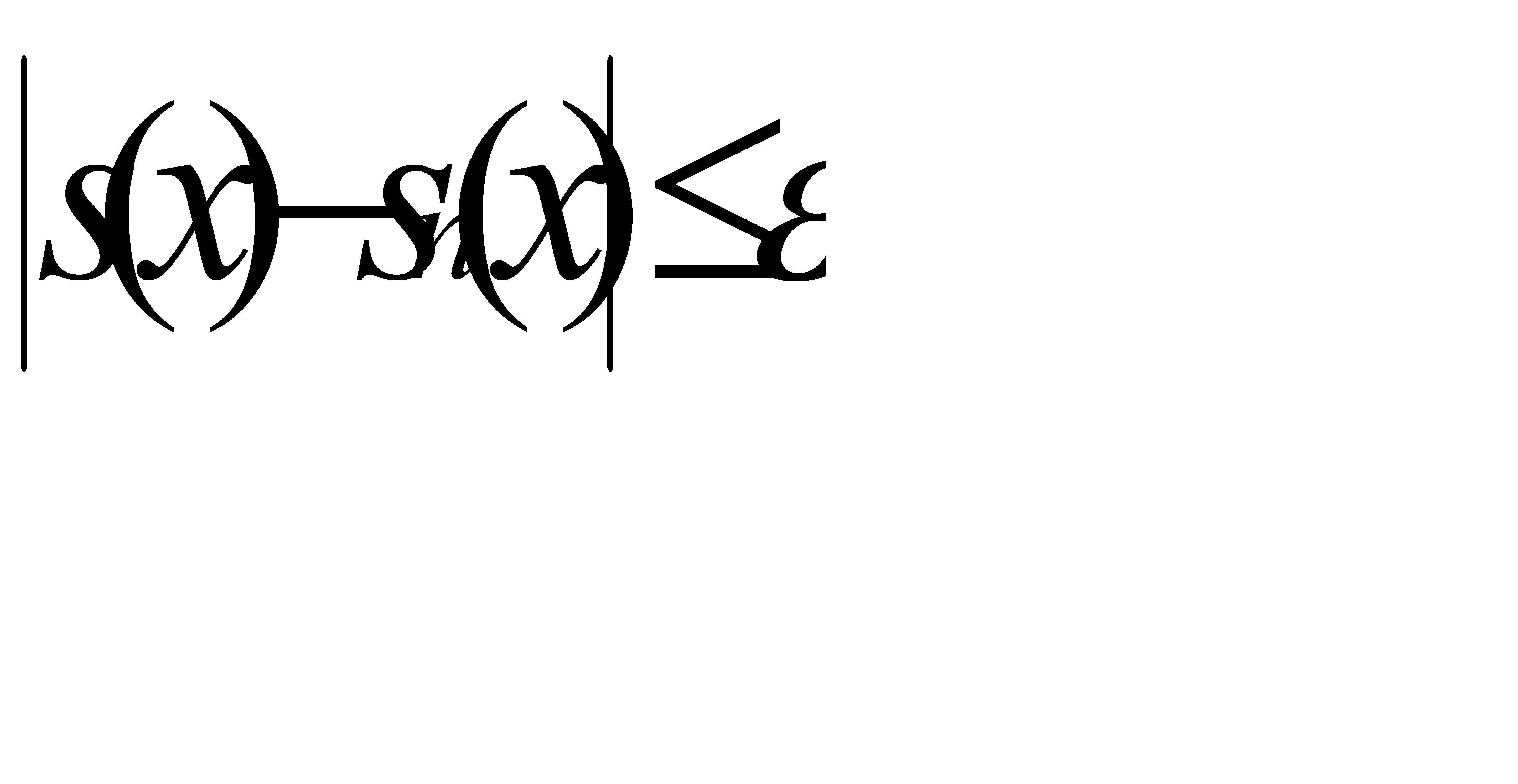(31.14)

Если мы рассмотрим графики функций y=s(x) (сумма ряда) и y=s_n(x) (частная сумма), то свойство равномерной сходимости означает, что для всех достаточно больших индексов n и для всех x графики суммы ряда и соответствующих его частных сумм отстоят друг от друга меньше чем на наперед заданную ε, т.е. эти графики равномерно (для всех х) близки (рис. 31.6)

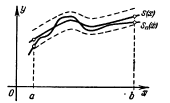
Рис. 31.6

Не всякий сходящийся на некотором отрезке ряд сходится равномерно. Имеется признак равномерной сходимости функциональных рядов (признак Вейерштрасса): Если числовой ряд с положительными членами сходится и для всех k, начиная с некоторого, 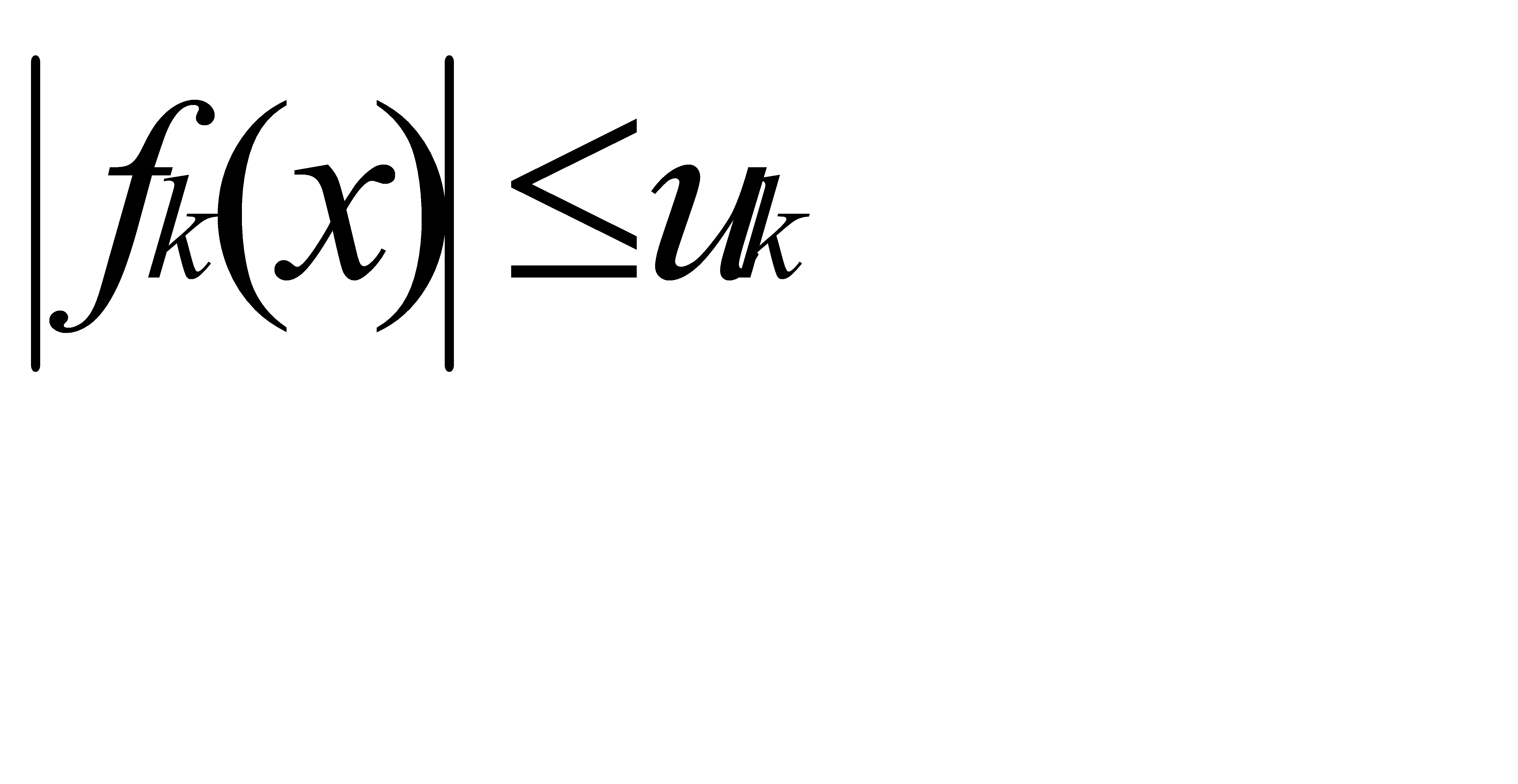, каково бы ни было х из отрезка [a,b], то ряд (31.11) сходится равномерно (и к тому же абсолютно) на [a,b]. Справедливы следующие важные теоремы: Если члены ряда (31.12) непрерывны на отрезке [a,b] и ряд сходится равномерно на этом отрезке, то

а) сумма ряда есть функция непрерывная,

б) ряд можно интегрировать почленно, т.е. для него справедлива формула (31.13)

2. Если ряд (31.12) сходится, его члены дифференцируемы и ряд 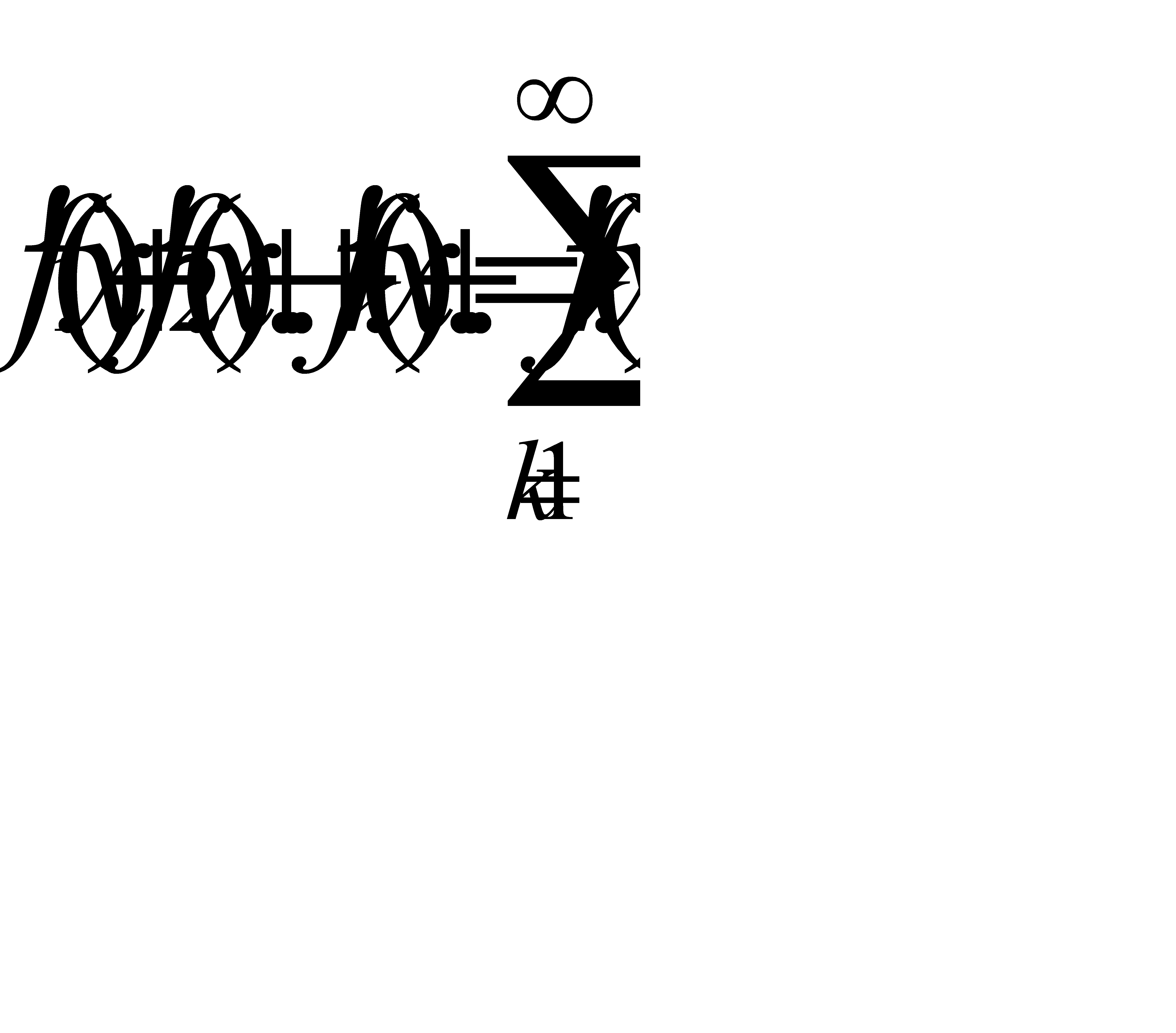равномерно сходится на [a,b], т о т.е. ряд (31.12) можно дифференцировать почленно.

Основная тригонометрическая система.

Ортогональность синусов и косинусов

Основной тригонометрической системой будем называть систему функций

1, cos x, sin x, cos 2x, sin 2x,…, cos nx, sin nx, … (31.15)

Все эти функции имеют общий период 2π (хотя cos nx и sin nx имеют и меньший период ). Установим несколько вспомогательных формул. При любом целом n≠0

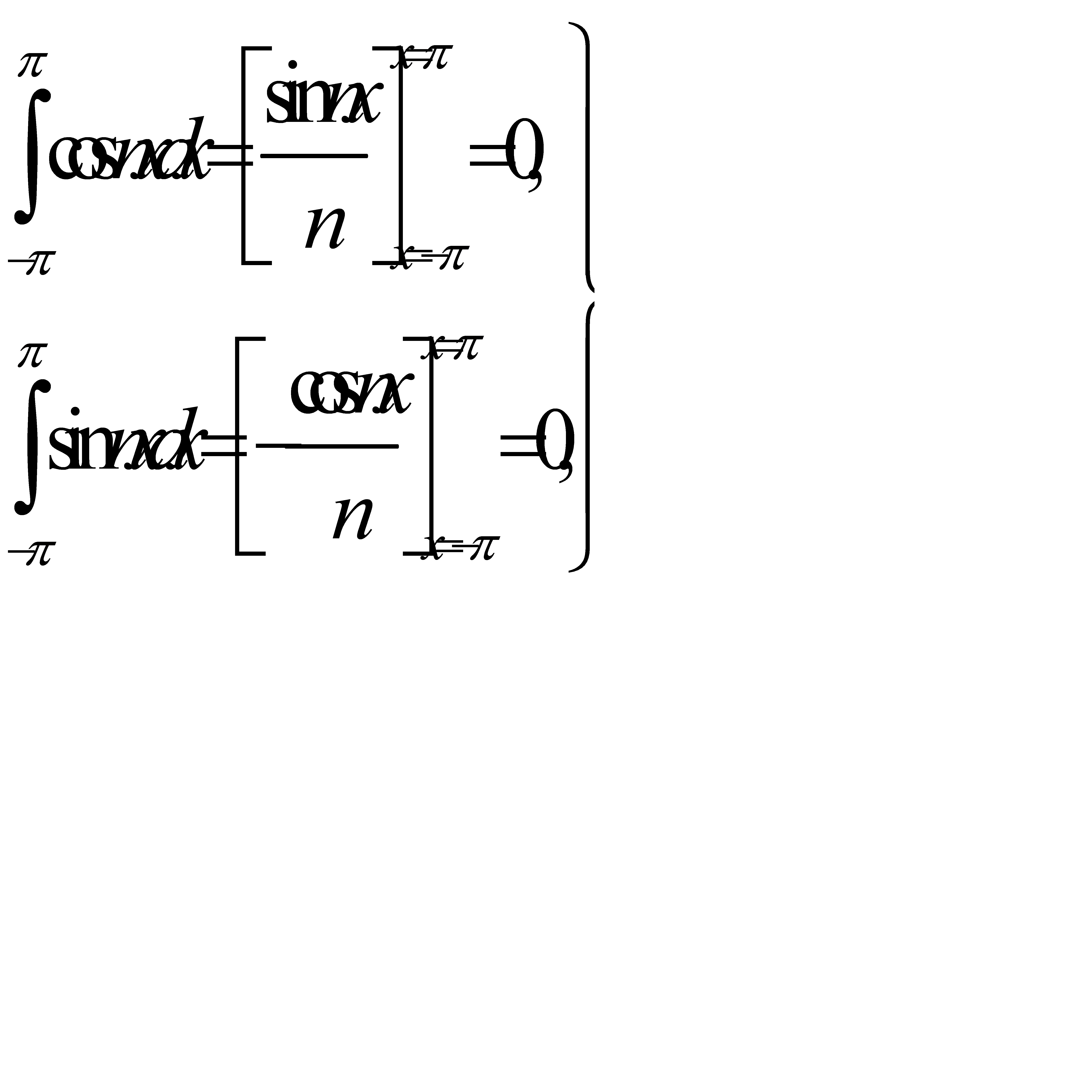(31.16)

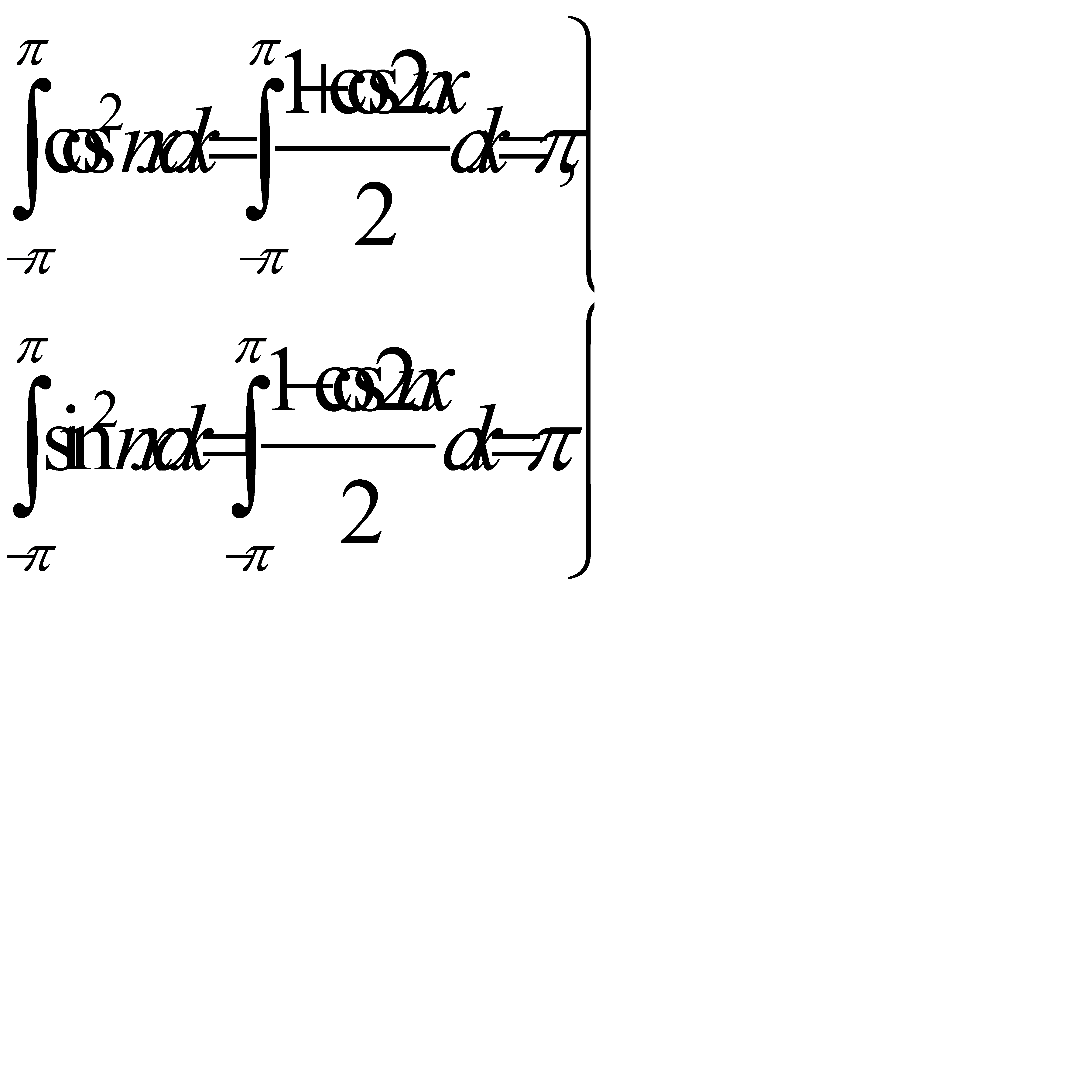(31.17)

В силу известных формул тригонометрии

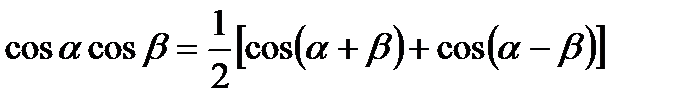
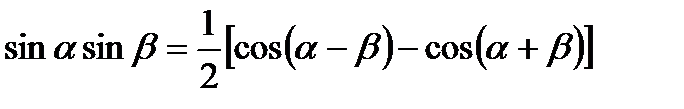
для любых целых n и m, n≠m,

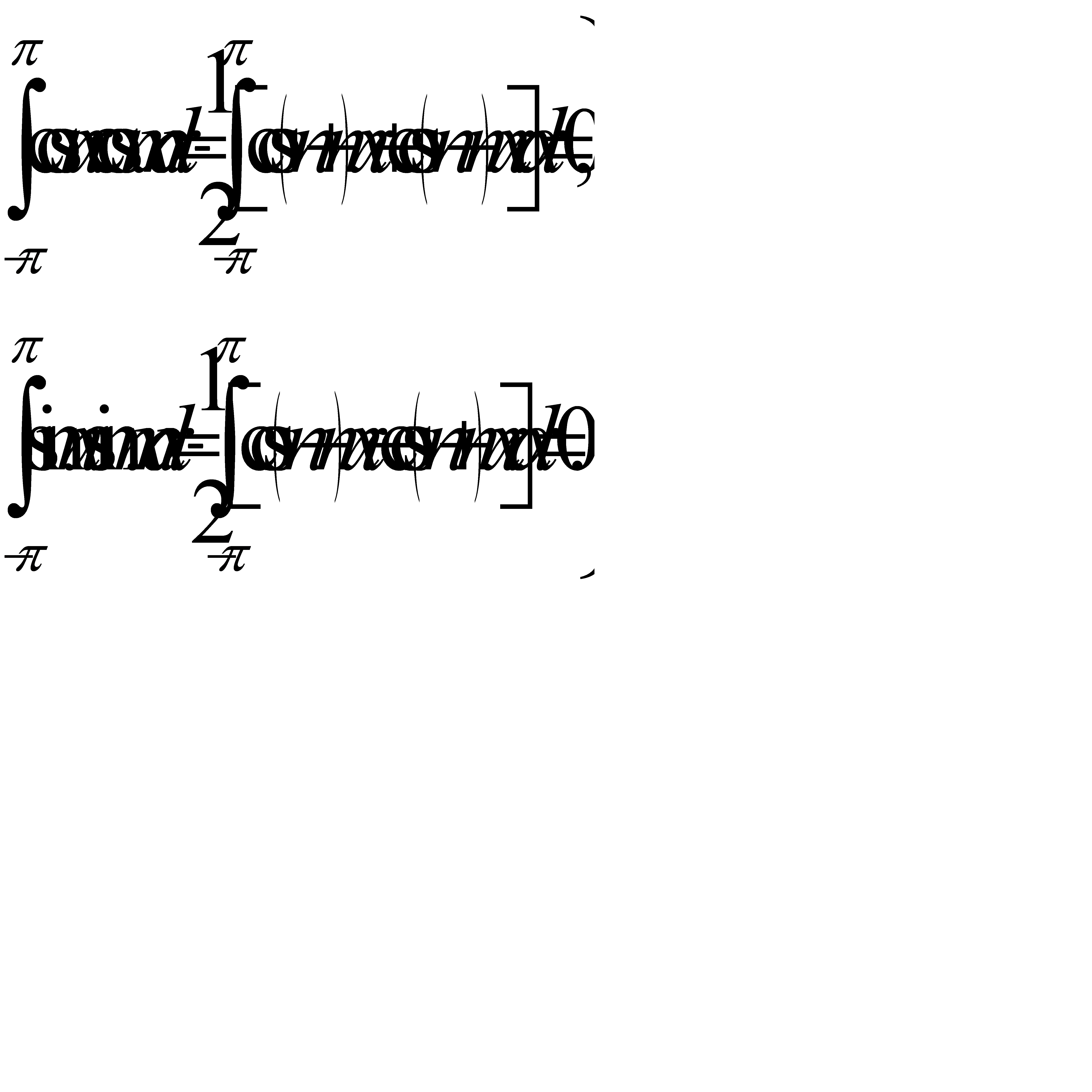(31.18)

Наконец в силу формулы

для любых целых n и m

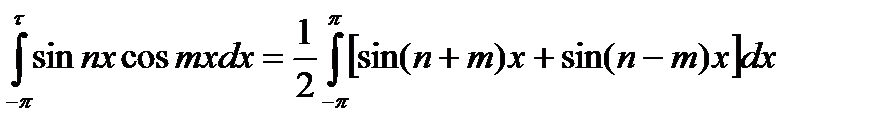(31.19)

Равенства (31.16), (31.18), (31.19) показывают, что интеграл от произведения двух любых различных функций системы (31.15), взятый по отрезку [-π,π], равен 0. Условимся говорить, что две функции φ(x) и ψ(x) ортогональны на отрезке [a,b], если . Приняв это определение, можем сказать, что функции системы (31.15) попарно ортогональны на отрезке [-π,π], или короче, система (31.15) ортогональна на [-π,π].Мы знаем, что для периодической функции интеграл по любому отрезку длины, равной периоду, имеет неизменное значение. Поэтому формулы (31.16)-(31.19) справедливы не только для отрезка [-π,π], но и для любого отрезка [a, a+2π]. Следовательно, система (31.15) ортогональна на всяком таком отрезке.

Ряд Фурье для функции периода 2π

Пусть для функции f(x) периода 2π имеет место разложение

(31.20)

Постоянное слагаемое здесь обозначено через 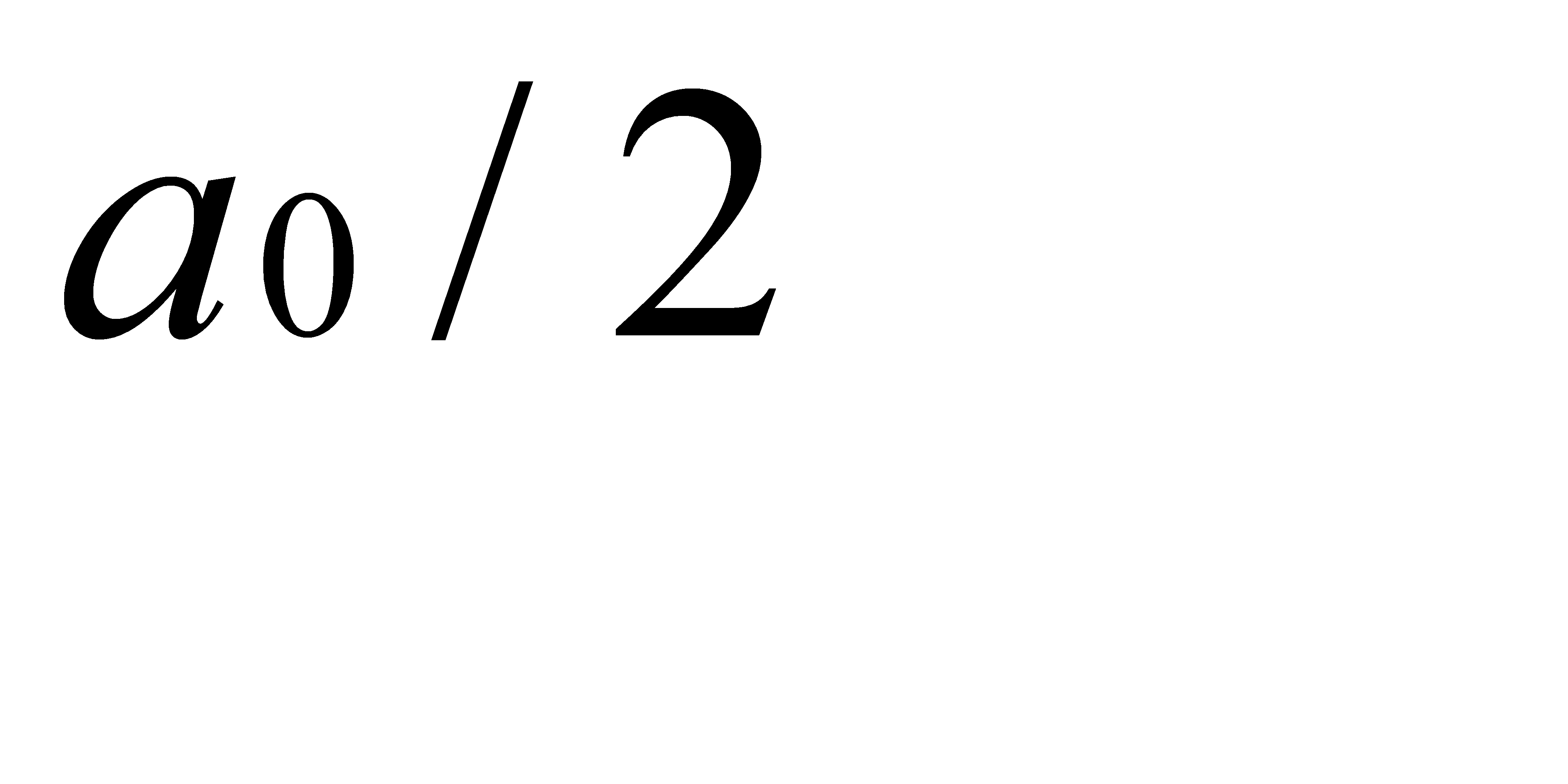для симметрии дальнейших формул. Поставим себе задачей вычислить коэффициенты a₀ ,a_k и b_k, k=1,2,…, зная функцию f(x). Для этого сделаем такое допущение: будем предполагать, что ряд (31.20) и ряды, которые мы сейчас получим, можно интегрировать почленно, т. е. для этих рядов интеграл от суммы равен сумме интегралов (тем самым предположена и интегрируемость функции f(x)). Интегрируя равенство (31.20) в пределах от —π до π, получим:

 

.

 

В силу (31.16) все интегралы под знаком суммы равны нулю. Поэтому

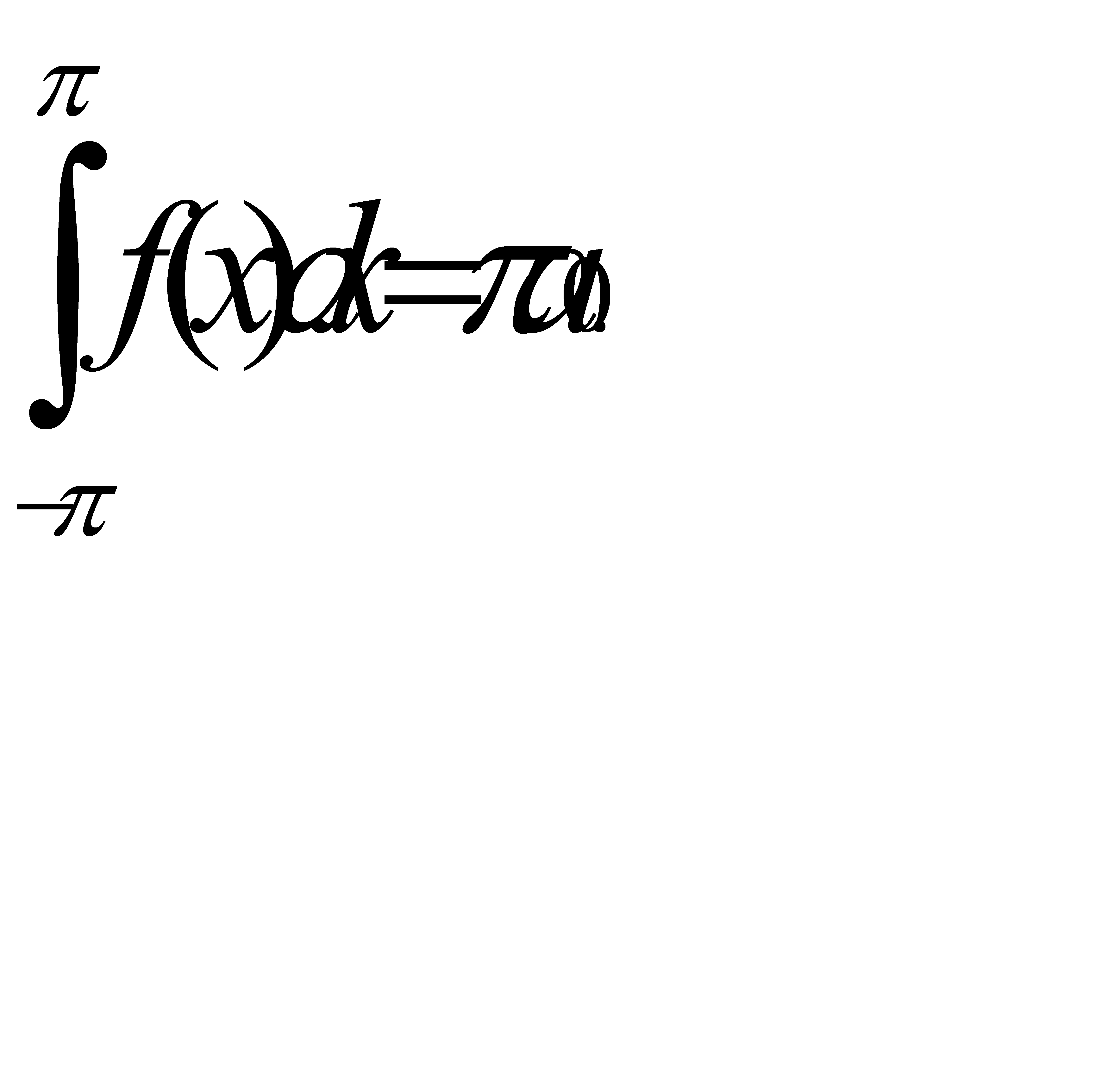(31.21)

Умножим обе части равенства (31.20) на cos nx и резуль­тат опять интегрируем в прежних пределах. Получим:

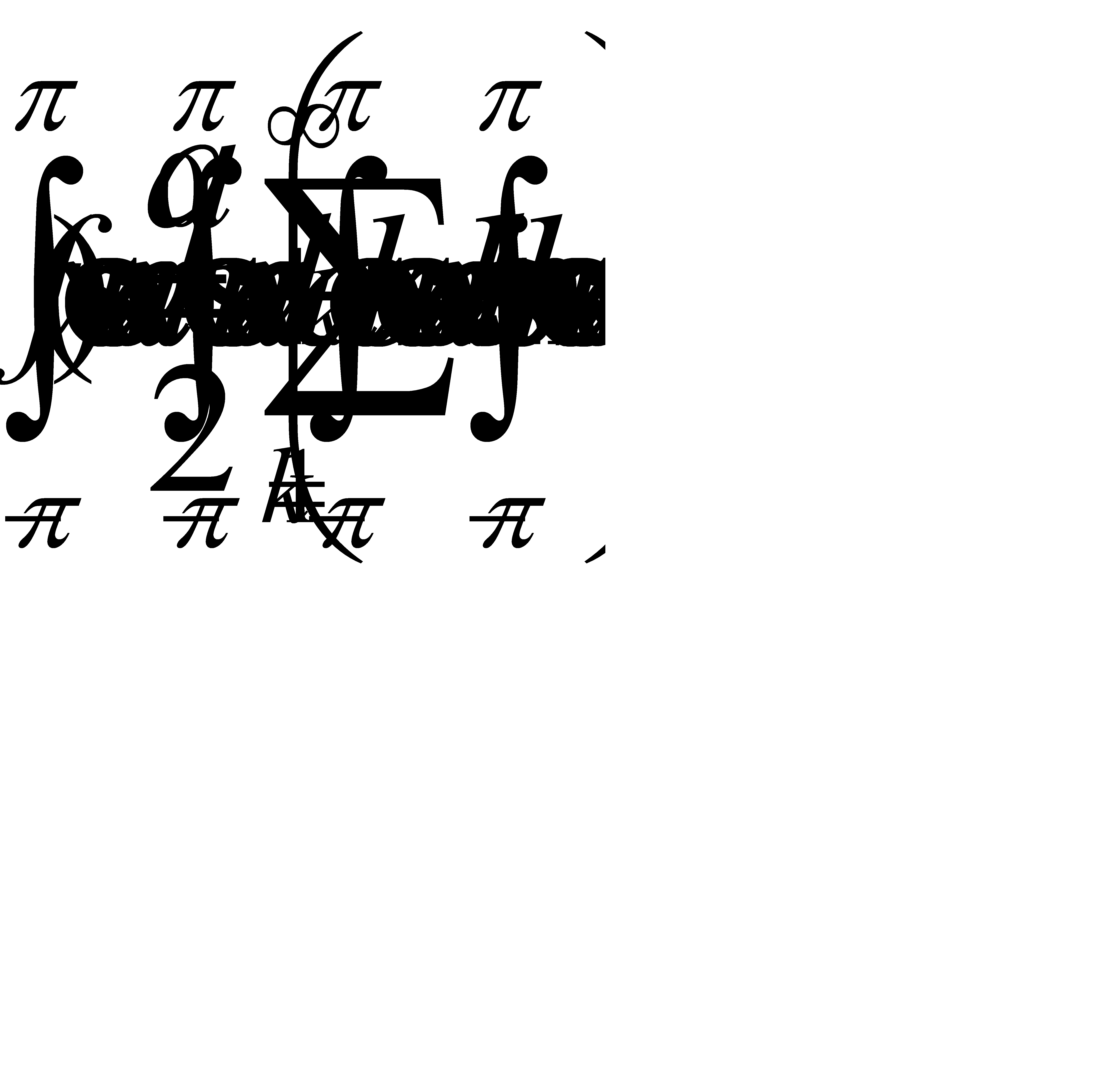
В силу (31.16) первый интеграл справа равен нулю. Так как функции системы (31.15) попарно ортогональны, то все интегралы под знаком суммы, кроме одного, оказы­ваются также равными нулю.

Останется лишь интеграл

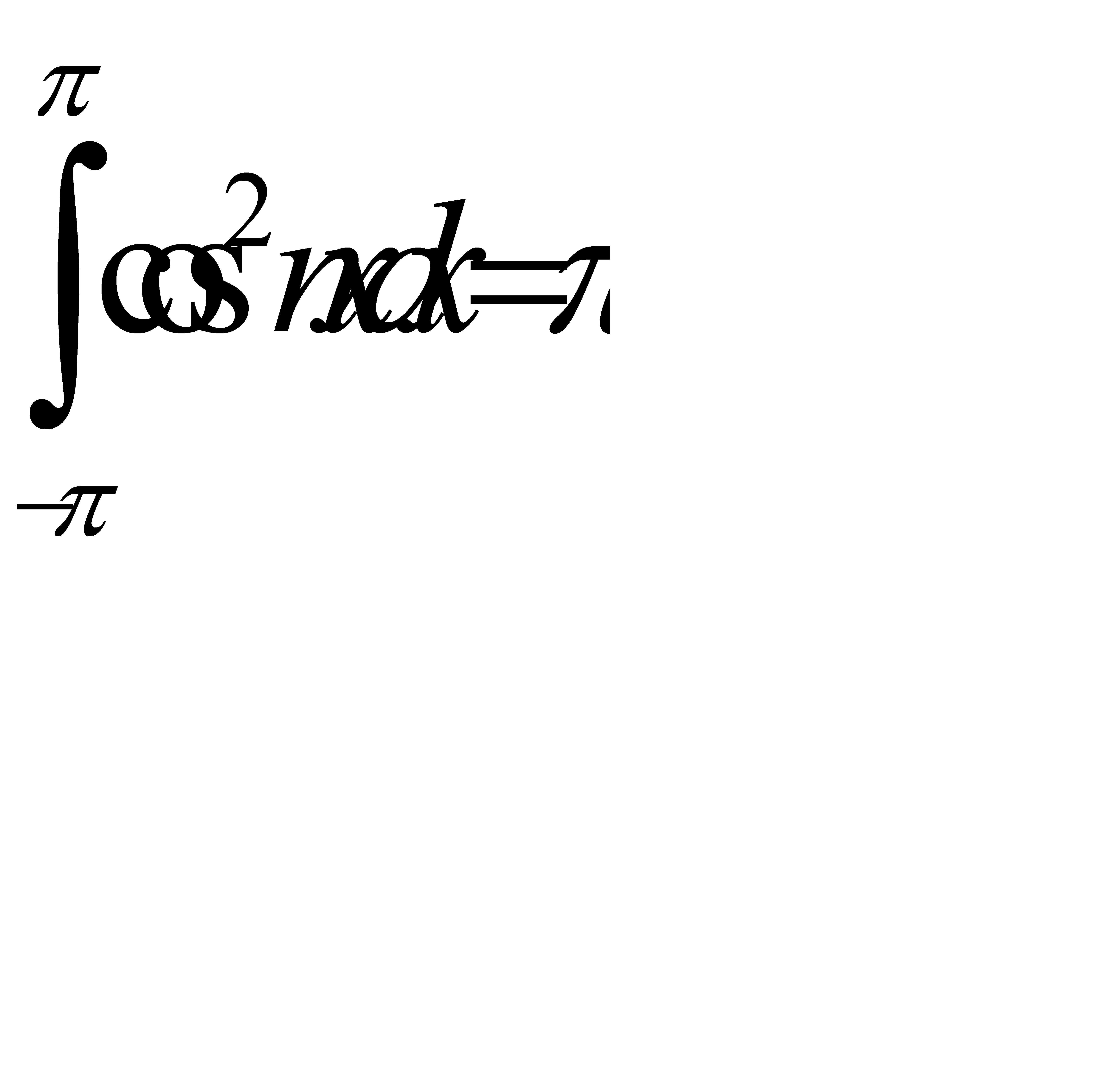(см. (31.17)), являющийся коэффициент при а_п. Таким образом,

(31.22)

Аналогичным приемом найдем, что

(31.23)

Из (31.21)—(31.23) вытекает

 

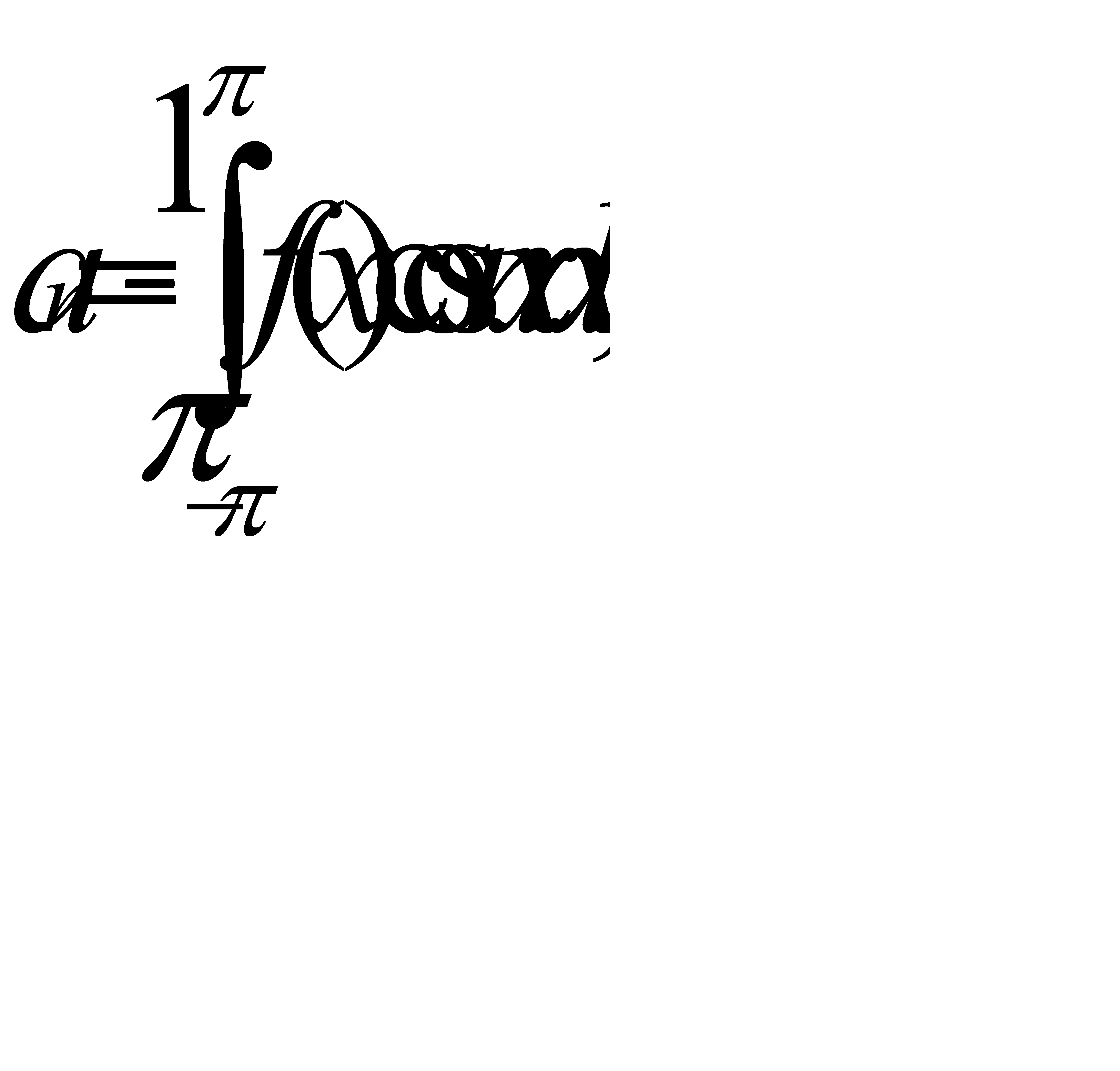
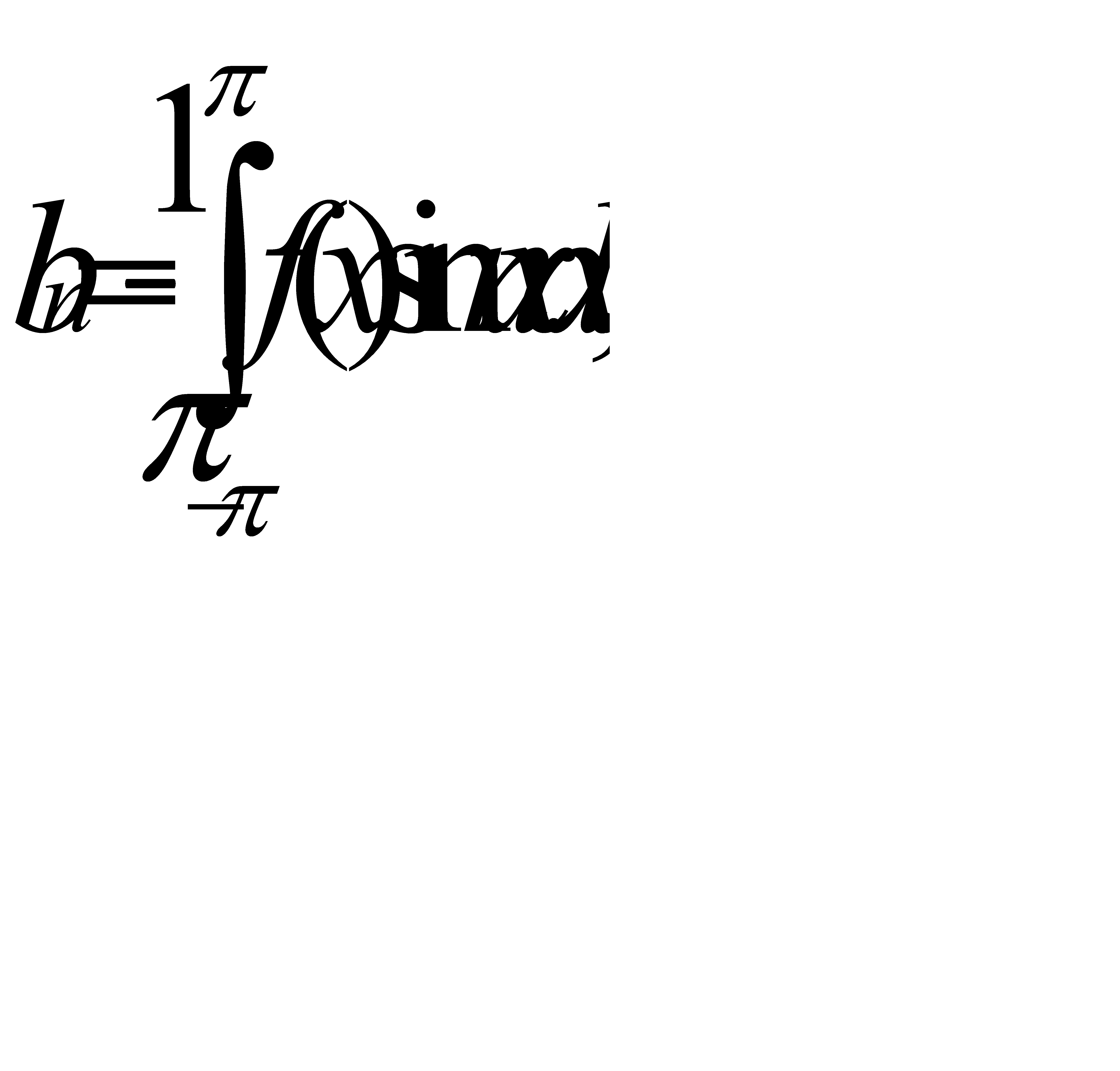(31.24)

(n=0, 1, 2, …) (n=1, 2, ….)

Итак, если f(х) интегрируема и может быть разложена в тригонометрический ряд, причем почленное интегрирование этого ряда и рядов, получающихся из него умножением на cos nx и sin nx (n= 1, 2, ...), возможно, то коэффициенты а_п и b_n вычисляются по формулам (31.24).

Пусть теперь задана некоторая интегрируемая функция периода 2 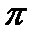, и мы хотим представить эту функцию в виде суммы тригонометрического ряда. Если такое представление вообще возможно (с выполнением требования почленной интегрируемости, упомянутого выше), то в силу изложенного коэффициенты а_п и b_n необходимо получаются по формулам (31.24). Поэтому в поисках тригонометрического ряда, имеющего своей суммой заданную функцию f(x), в первую очередь естественно обратить внимание на тот ряд, коэффициенты которого вычисляются по формулам (31.24), и посмотреть, не обладает ли он нужным нам свойством. Мы увидим далее, что для обширного класса функций это так и будет. Коэффициенты а_п и b_n, вычисленные по формулам (31.24), называются коэффициентами Фурье для функции f(x), а тригонометрический ряд с такими коэффициентами называется ее рядом Фурье. Заметим, кстати, что в формулах (31.24) интегрируются функции периода 2я. Поэтому отрезок интегрирования [—π,π] может быть заменен любым другим отрезком длины 2π , и мы наряду с формулами (31.24) получаем:

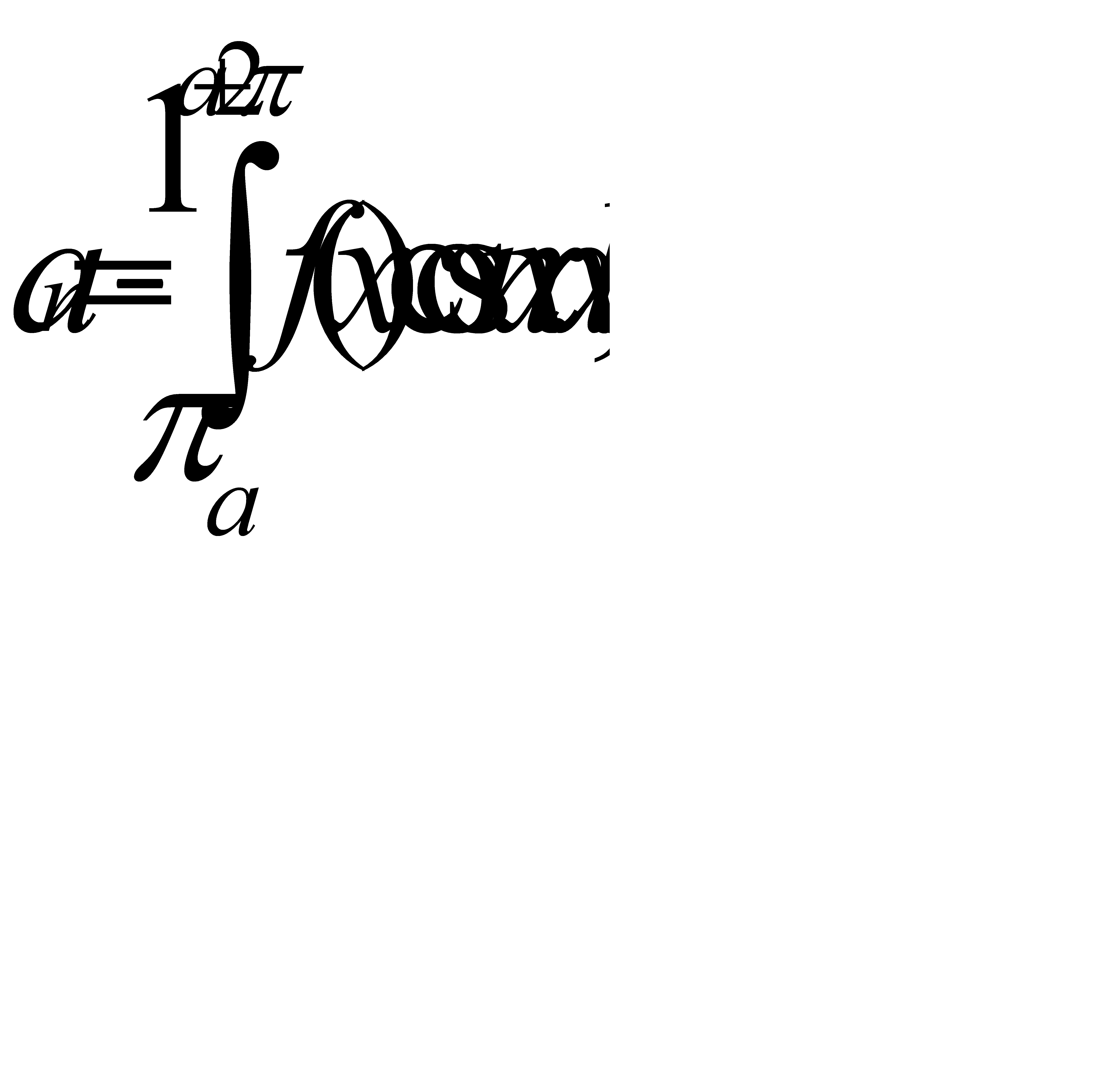(n=0, 1, 2, …),

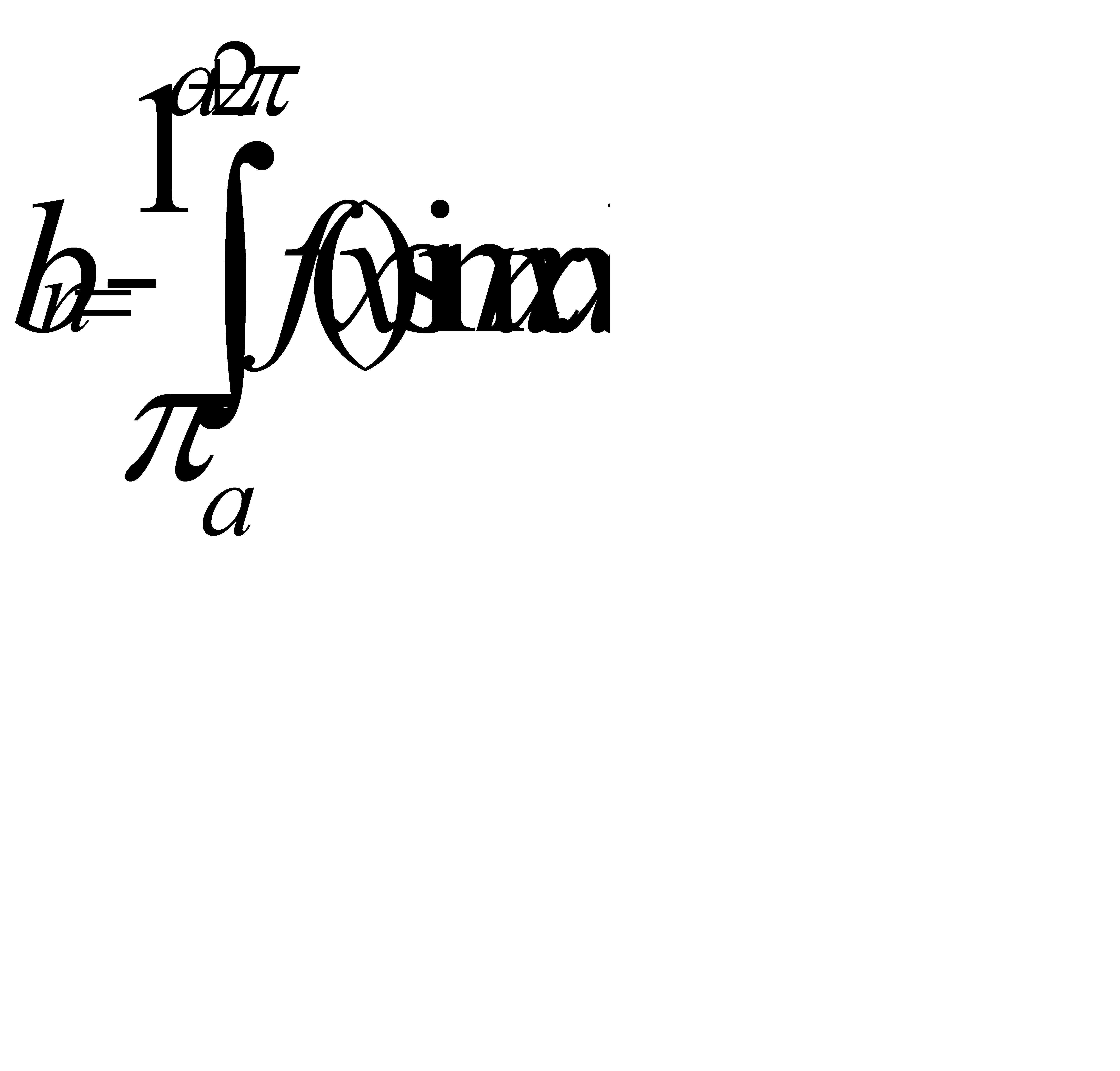(n=1, 2, ….) (31.25)

Изложенное выше делает естественным особое внимание к рядам Фурье. Составив ряд Фурье для функции f(x)и не предрешая вопроса о его сходимости к f(x), мы пишем:

. Такая запись означает лишь, что функции f(x) соответствует ряд Фурье, написанный справа. Знак « ~ » можно заменить знаком « = » только тогда, когда нам удастся доказать сходимость ряда и равенство его суммы функции f(x). Из предшествующих рассуждений легко вытекает следующая, оказывающаяся часто полезной.

Теорема 1. Если для функции f(x) периода 2я имеет место разложение в некоторый равномерно сходящийся на всей оси Ох тригонометрический ряд, то этот ряд есть ряд Фурье для f(x).

Рассмотрим равенство

(31.26)

и покажем, что ряд справа сходится равномерно.

Положим: .

Пусть ε — произвольное положительное число. Если ряд (31.20) сходится равномерно, то существует число N такое, что для всех m≥N 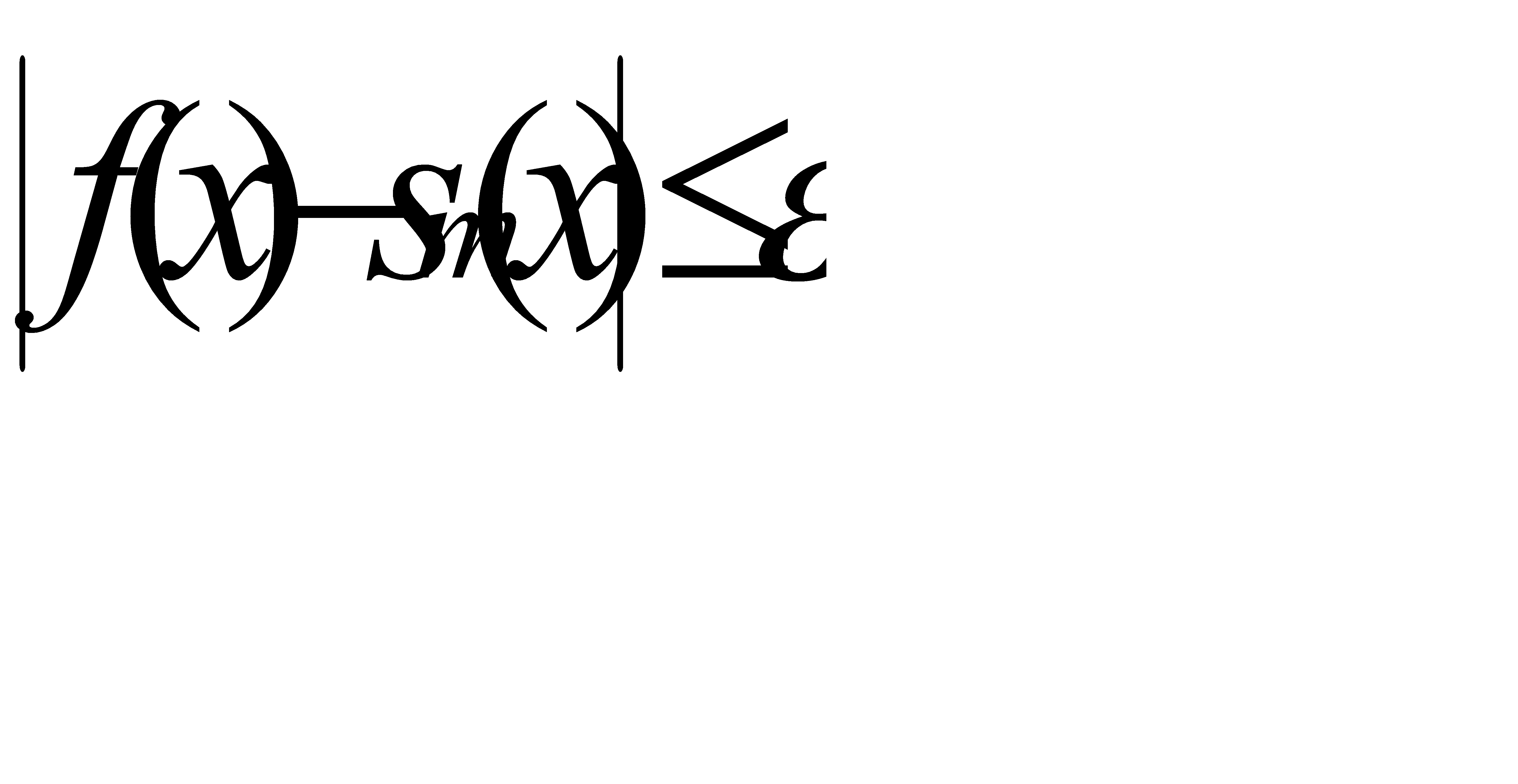. Произведение sin x cos x, очевидно, является т-й частной суммой для ряда (31.26). Поэтому из соотношения

,

справедливого для всех m≥N, и вытекает равномерная сходимость ряда (31.26). В таком случае этот ряд можно почленно интегрировать, а интегрирование дает равенство (31.22). Аналогично доказывается равенство (31.23). Тем самым для коэффициентов а_n и b_n доказаны формулы (31.24). Это и означает, что ряд (31.20) есть ряд Фурье для f(x). Современная теория рядов Фурье позволяет доказать следующее более общее предложение, доказательство которого мы приводить не будем из-за его сложности.

Теорема 2. Если абсолютно интегрируемая функция f(x) периода 2π допускает разложение в некоторый тригонометрический ряд, сходящийся к ней всюду за исключением, быть может, конечного числа значений (для одного периода), то этот ряд есть ряд Фурье для f(x).

Эта теорема подтверждает высказанное выше соображение, что в поисках тригонометрического ряда, имеющего своей суммой заданную функцию, в первую очередь следует обращаться к ряду Фурье.

Ряд Фурье для функции, заданной

на отрезке длины 2π

В приложениях очень часто возникает задача о разложении в тригонометрический ряд функции f(x),заданной лишь на отрезке [—π,π]. Здесь, следовательно, о периодичности f(x) нет и речи. Это тем не менее нисколько не мешает нам написать для нее ряд Фурье, ибо в формулах (31.24) фигурирует лишь отрезок [—π,π]. Вместе с тем, если периодически продолжить f(x) с отрезка [—π, π] на всю ось Ох, то получим периодическую, совпадающую с f(x) на [-π, π] функцию, для которой ряд Фурье будет тождественным с рядом Фурье для f(x). К тому же, если ряд Фурье для f(x) оказывается сходящимся к ней, то его сумма, будучипериодической функцией, даст как раз упомянутое периодическое продолжение f(x) с отрезка [—π, π] на всю ось Ох. Таким образом, говорить о ряде Фурье для f(x) заданной на [—π, π], —это все равно, что говорить о ряде Фурье для функции, получающейся из f(x) периодическим продолжением ее на ось Ох. Отсюда вытекает, что признаки сходимости рядов Фурье достаточно формулировать для периодических функций. В связи с упомянутым периодическим продолжением f(x) с отрезка [—π, π] на ось Ox уместно сделать следующее замечание. Если f(-π)= f(π), то периодическое продолжение никаких затруднений не встречает (рис.31.7, а).

 

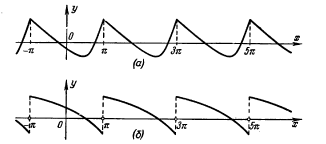
Рис.31.7

 

При этом, если f(x) была непрерывной на отрезке [-π,π], то ее продолжение будет непрерывным на всей оси Ох. Если же f(-π)≠f(π), то, не изменяя значений f(-π)и f(π)мы не сможем осуществить нужное продолжение, так как по смыслу периодичности f(-π)должно совпадать c f(π). Обойти это затруднение мы можем двояким образом: во-первых, исключить вовсе из рассмотрения значения f(x) при x=- π и x= π, сделав тем самым функцию неопределенной для этих значений и, следовательно, сделав неопределенным периодическое продолжение f(x) для всех значений x вида (2k+1) π (k=0, ±1, ±2…); во-вторых, изменить выгодным нам образом значения функции f(x) при x=- π и x= π ,сделав их равными. Важно отметить, что и в том и в другом случаях коэффициенты Фурье будут иметь те же значения, что и сначала. Действительно, изменение значений функции в конечном числе точек, или даже неопределенность ее в этих точках,— не может оказать влияния на величину интеграла, в частности на величину интегралов (31.24), определяющих коэффициенты Фурье. Таким образом, независимо от того, осуществим мы указанную модификацию функции f(x) или нет, ряд Фурье для нее остается неизменным. Нужно отметить, что при f(-π)≠f(π) и при непре­рывности f(x)на отрезке [—π, π] периодическое про­должение f(x) на всю ось Ох будет иметь разрывы во всех точках вида x=(2k+1) π (k=0, ±1, …), как бы мы ни изменяли значения функции при x=- π и x= π . К каким значениям следует ожидать сходимости ряда Фурье в этих точках при f(-π)≠f(π), - это вопрос особый, и мы решим его позднее. Пусть теперь f(x)задана на произвольном отрезке [а,а+2 π ] длины 2 π и ее требуется разложить в тригонометрический ряд. Коэффициенты Фурье вычисляем по формулам (31.25). Как и выше, приходим к выводу, что говорить о ряде Фурье для f(x) или для функции, получающейся из нее периодическим продолжением на всю ось Ох, - это одно и то же. При этом непрерывная на отрезке [а,а+2π] функция f(x) при f(a)≠f(a+2 π) дает продолжение, разрывное в точках вида x=a+2kπ (k=0, ±1,…).

Правый и левый пределы функции в точке.

Точки разрыва первого рода

Введем обозначения:

 

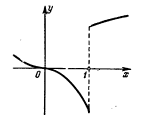
Рис. 31.8

(если эти пределы существуют и конечны). Первый из этих пределов называется пределом f(x) в точке х₀ слева, второй — пределом f(x) в точке х₀ справа. В точках непрерывности, по самому определению понятия непрерывности, эти пределы существуют, причем

f(x₀ - 0) = f(x₀) = f(x₀ + 0). (31.27)

Если х₀ есть точка разрыва функции f(x), то пределы справа и слева (оба или один из них) могут существовать в одних случаях и не существовать в других. Если оба предела существуют, то говорят, что точка х₀ есть точка разрыва первого рода для функции f(x). Если же хотя бы один предел не существует, то точка х₀ называется точкой разрыва второго рода. Нас будут интересовать точки разрыва первого рода. Если х₀ — такая точка, то величина

ð = f(x₀ + 0) - f(x₀ - 0) (31.28)

называется скачком функции f(x) в точке х₀.

Для пояснения сказанного рассмотрим пример.

Пусть

 

(31.29)

На рис. 31.8 изображен график этой функции.

Значение функции при х = 1 изображено маленьким кружком. Для пределов слева и справа при x=1, очевидно, имеем: f(1 - 0) = - 1, f(1 + 0) = 1. Следовательно, для скачка функции получаем: ð = f(1+0) - f(1 - 0) = 2, что вполне согласуется с наглядным представлением о скачке Точки разрыва первого рода могут появиться, например, при периодическом продолжении непрерывной на отрезке [-π,π] функции f(x) с этого отрезка на всю ось Ох в случае, когда f(-π) ≠ f(π). При этом все скачки оказываются равными числу ð = f(-π) - f(π).

Гладкие и кусочно-гладкие функции

Функцию f(x) называют гладкой на отрезке [а, b], если она на этом отрезке обладает непрерывной производной. На геометрическом языке это означает, что при перемещении вдоль кривой у = f(x) направление касательной изменяется непрерывно, без скачков (рис. 9, а). Таким образом, график гладкой функции представляет собой плавную кривую, лишенную угловых точек. Функцию f(x) называют кусочно-гладкой на отрезке [а, b], если она сама и ее производная либо непрерывны на этом отрезке, либо допускают на нем лишь разрывы первого рода, и притом в конечном числе. График кусочно-гладкой функции представляет собой непрерывную или разрывную кривую, которая может иметь конечное число угловых то­чек (в них происходит скачок производной); с приближением к такому углу или к месту разрыва (с той или иной стороны) направление касательной стремится к определенному положению На рис. 31.9,б и 31.9, в изображены графики непрерывной и разрывной кусочно-гладких функций. Гладкие функции мы будем рассматривать в дальнейшем как частный случай функций кусочно-гладких.

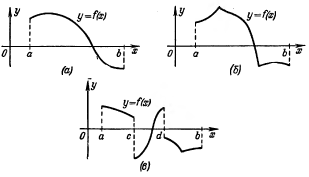
Рис.31.9

Непрерывная или разрывная функция f(x), заданная на всей оси Ох, называется кусочно-гладкой, если она такова для каждого отрезка конечной длины. В частности, это относится к периодическим функциям.

Всякая кусочно-гладкая функция f(x) (непрерывная или разрывная) ограничена и имеет ограниченную производную всюду, за исключением угловых точек и точек разрыва (во всех этих точках f'(x) не существует).

Признак сходимости ряда Фурье

Мы сформулируем наиболее употребительный признак сходимости ряда Фурье.

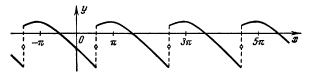
Рис. 31.10

Ряд Фурье кусочно-гладкой (непрерывной или раз­рывной) функции f(x) периода 2π сходится для всех значений х, причем его сумма равна f(x) в каждой

точке непрерывности и равна числу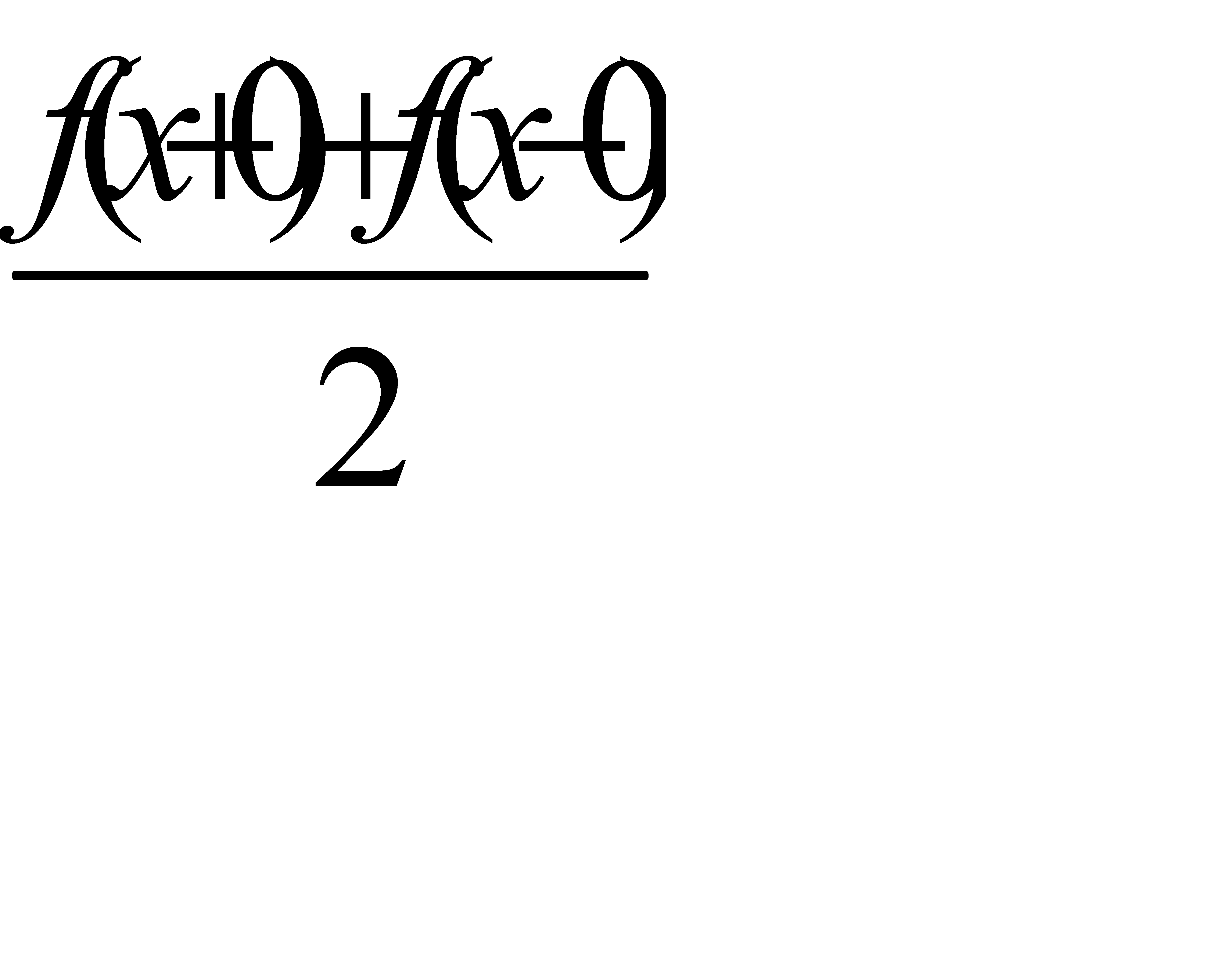

(среднее арифметическое предельных значений справа и слева) в каждой точке разрыва (рис. 31.10).

Если f(x) всюду непрерывна, то ряд сходится абсо­лютно и равномерно.

Пусть функция f(x) задана лишь на [-π, π], является кусочно-гладкой на этом отрезке и непрерывна в его концах. Ряд Фурье для f(x) совпадает с рядом Фурье для функции, являющейся периодическим продолжением f(x) на всю Ох. Но такое периодическое продолжение в нашем случае, очевидно, приведет к функции f(x), кусочно-гладкой на всей оси Ох. Поэтому из сформулированного нами признака вытекает, что ряд Фурье будет всюду сходящимся. В частности, это будет иметь место на интересующем нас отрезке [-π, π], причем для - π < х < π ряд будет cходиться к f(x) в точках непрерывности и к значению в точках разрыва. Что же будет происходить в концах отрезка [-π, π]? Возможны два случая:

1. f(-π) = f(π). Здесь периодическое продолжение приводит, очевидно, к функции, непрерывной в точках -π и π (и вообще во всех точках вида x = (2k+1)π (k = 0, ±1, ±2, ...)). В силу нашего признака и в кон­цах отрезка ряд будет сходиться, следовательно, к f(x).

2. f(-π) ≠ f(π). Здесь периодическое продолжение приводит к функции, разрывной в точках -π и π (а также во всех точках вида x = (2k+l)π (k = 0, ±1, ±2, ...)), причем для продолженной f(x) очевидно:f(-π - 0) = f(π), f (-π + 0) =f (-π), f(π + 0) = f(-π), f(π - 0) = f(π) (рис. 39.11). Поэтому при х = - π и х = π ряд будет сходиться к значениям

 

 

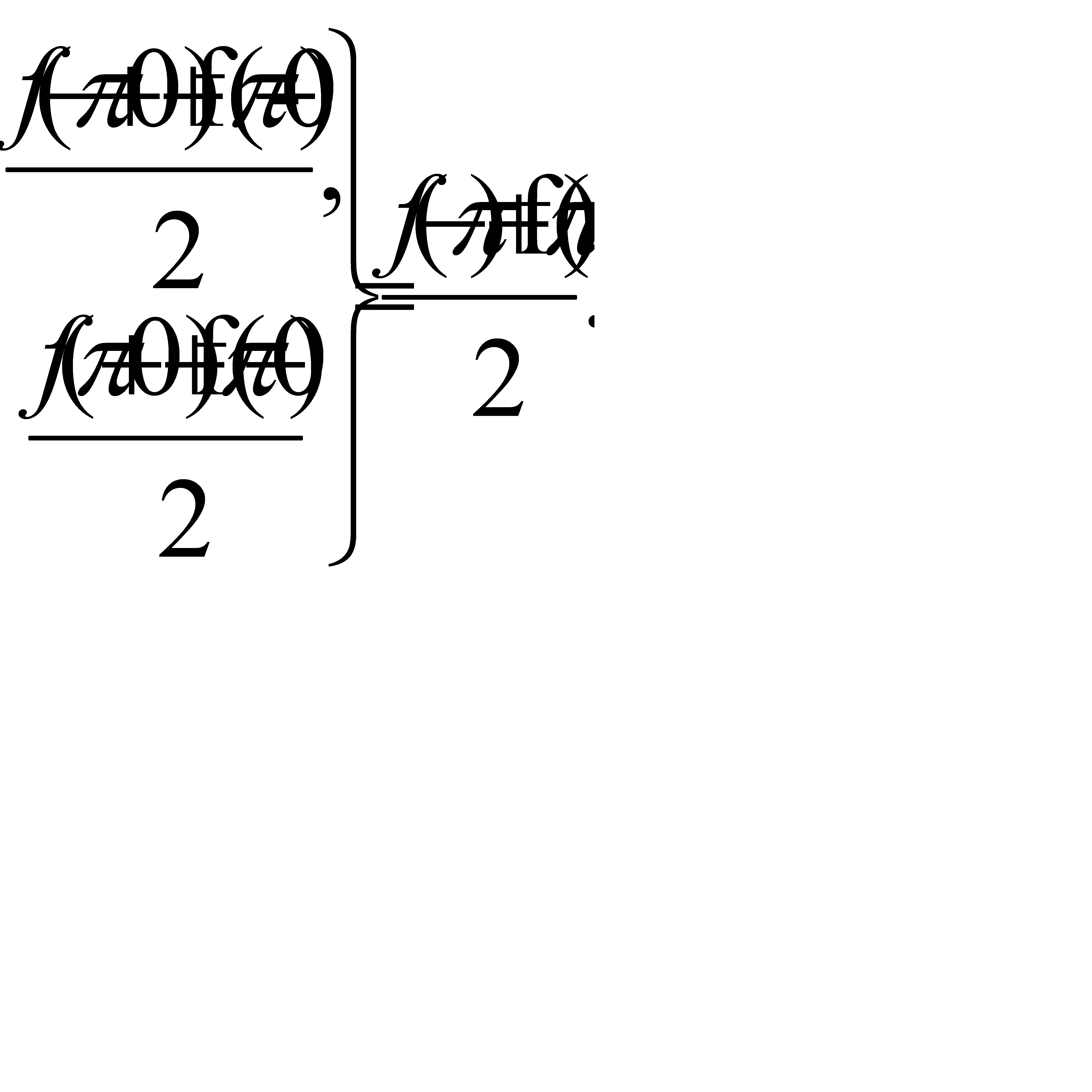
(31.30)

Таким образом, для функции f(x), заданной на отрезке [-π, π] и непрерывной при х =-π и х = π, ряд Фурье ведет себя в этих точках, как и в прочих точках непрерывности функции, если f(-π) = f(π). Если же f(-π) ≠ f(π) то ряд заведомо не может сходиться к f(х) при х =-π и х = π. Поэтому в последнем случае задачу о разложении f(x) в ряд Фурье имеет смысл ставить не для - π ≤ х ≤ π, а для - π < х < π. Аналогичное замечание можно сделать относительно ряда Фурье для функции, заданной на отрезке вида [a, а + 2π], где а — любое число.

 

 

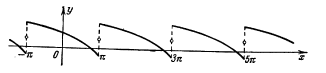
Рис. 31.11

Впрочем, при решении каждой конкретной задачи, когда читатель построит график периодически продол­женной функции (а это всегда рекомендуется!) и вспом­нит сформулированный выше признак, то вопрос о по­ведении ряда Фурье в концах отрезка сразу станет ясным.

Четные и нечетные функции

Пусть f(х) задана на всей оси Ох или же на некотором отрезке, симметричном относительно начала координат.

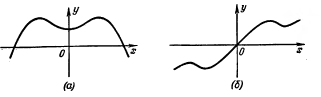
Рис. 31.12.

Скажем, что f(x) есть четная функция, если для каждого х: f(-x) = f(x). Из этого определения вытекает, что график всякой четной функции у = f(х) симметричен относительно оси Оу (рис. 31.12, а). При любом l (лишь бы f(x) была определена и интегрируема на отрезке [ - l, l]).

Функцию f(x) назовем нечетной, если для

каждого x: f(-x) = -f(x). Для нечетной функции, в частности, f(-0)=-f(0) и, следовательно, f(0) = 0. График всякой нечетной функции у = f(х) симметричен относительно точки О (см. рис. 31.12,б). При любом l (лишь бы f(x) была определена и интегрируема на отрезке

[-l,l]). Из определения четных и нечетных функций легко вытекает:

а) Произведение двух четных или двух нечетных функций есть функция четная.

б) Произведение четной и нечетной функций есть функция нечетная.

Ряды по косинусам и ряды по синусам

Пусть f(x) — четная функция, заданная на отрезке [-π, π] (или же четная периодическая функция).

Так как cos(nх) (п = 0, 1, 2, ...) есть функция, очевидно, четная, то по свойству а) будет четной и функция f(x)cos(nx). Функция sin(nx) (п = 1, 2, ...) нечетна. Поэтому по свойству б) нечетна и функция f(x) sin(пх).

Тогда в силу для коэффициентов Фурье четной функции f(x) получаем:

 

 

 

 

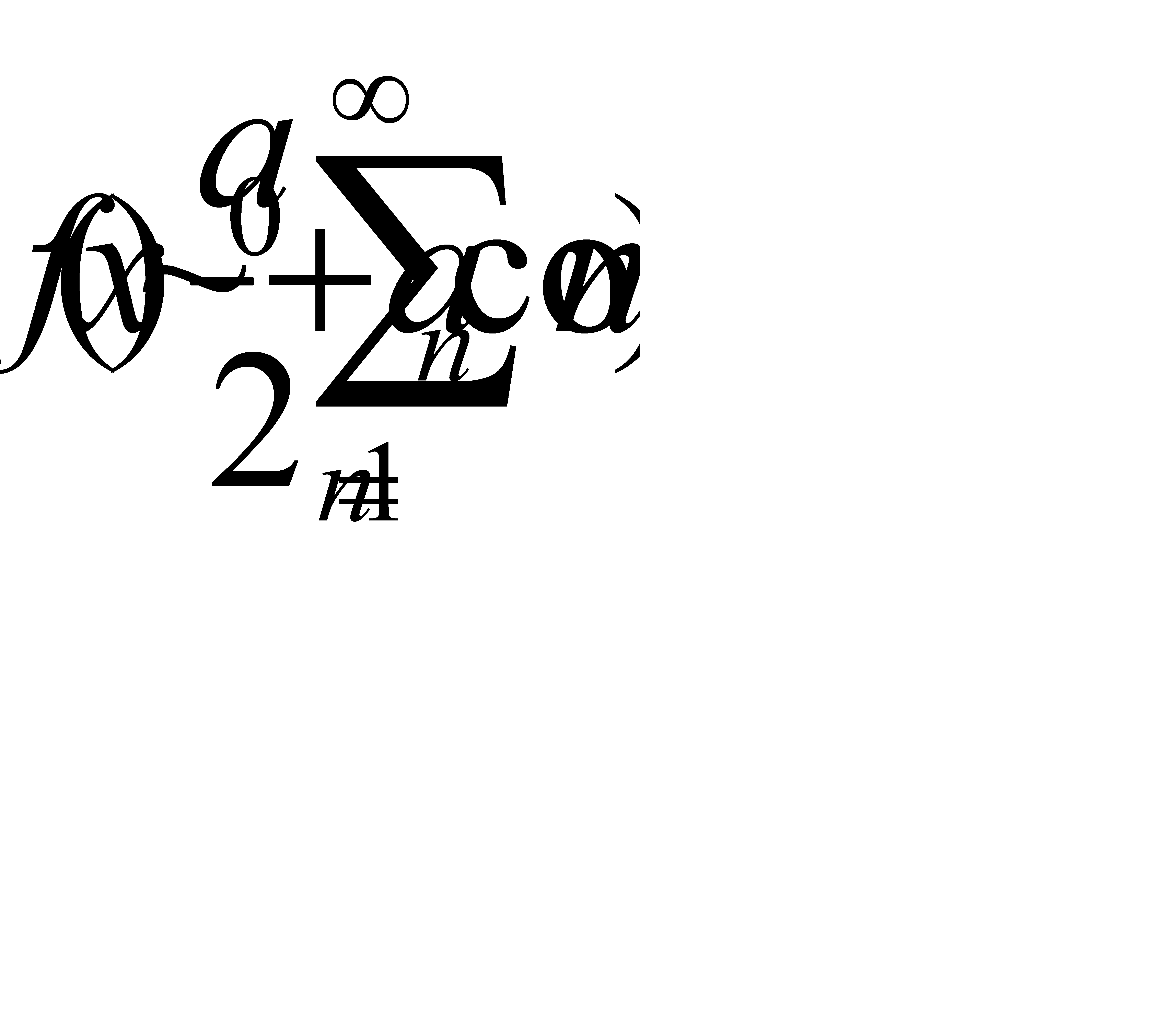
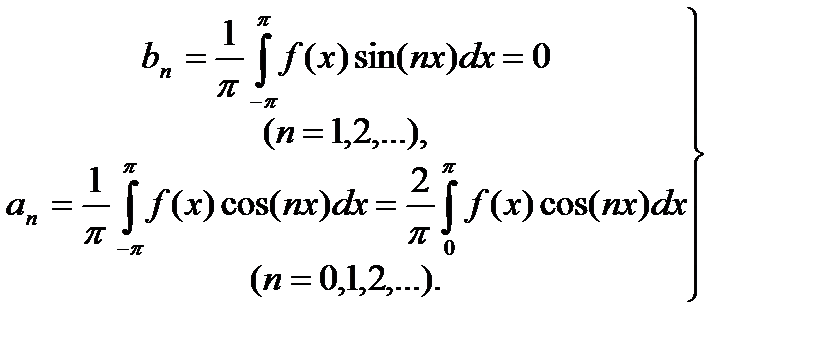
(31.31)

 

Следовательно, для четной функции ряд Фурье содержит лишь косинусы, т. е.коэффициенты а_п вычисляются по формулам (31.31).

Пусть теперь f(x)—нечетная функция, заданная на отрезке [-π,π] (или же нечетная периодическая функция), cos(nх) (n = 0, 1, 2, ...) — четная функция. По свойству б) 31.11 функция f(x)cos(nx) нечетная. Функция sin(nх) (п=1, 2, ...) нечетна. Поэтому по свойству а) 31.11 функция f(x) sin(пх) оказывается четной. Тогда коэффициенты Фурье нечетной функции f(x):

 

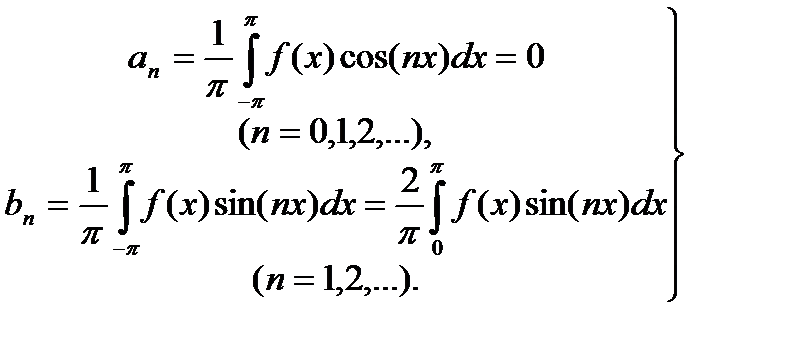
(31.32)

 

 

Таким образом, ряд Фурье нечетной функции содержит лишь синусы, т. е.