Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Комплексная плоскость.

Понятие области на комплексной плоскости.

Понятие предела последовательности комплексных чисел

Ранее мы определили комплексную плоскость как плоскость XOY, которая служит для изображения комплексных чисел. Расширенной комплексной плоско­стью называется плоскость XOY, до­полненная идеальной (воображаемой) точкой z=∞, называемой бесконечно удаленной точкой. Чтобы лучше понять роль этой точки, построим в пространстве OXYZсферу с центром в точке М(0;0;1/2) радиуса R=1/2 (рис.39.1).

 

 

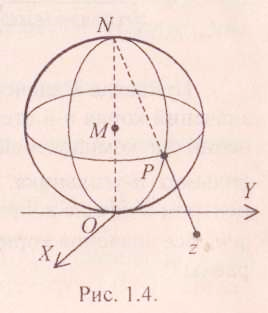
Рис.39.1.

Любую точку z = x+iy соединим прямой с точкой N на сфере. Точка Р пересечения этой прямой со сферой называется сте­реографической проекцией точки z на сферу.

Если | z | →∞, то точка Р приближается к точке N. По­этому естественно считать точку N стереографической проек­цией бесконечно удаленной точки. Роль точки z= ∞ подобна роли точки N на сфере.

Окрестностью точки z₀ называется совокупность внут­ренних точек любого круга с центром в точке z₀ радиуса ρ. то есть совокупность точек z, удовлетворяющих неравенству |z-z₀|<ρ.

Окрестностью бесконечно удаленной точки называется совокупность точек, лежащих вне любого круга с центром в начале координат, то есть множество, точек, удовлетворяющих неравенству |z|> R.

Пусть Е - множество точек комплексной плоскости. Точ­ка z называется внутренней точкой множества Е, если сущест­вует окрестность этой точки, принадлежащая множеству Е. Точка z называется граничной точкой множества Е, если лю­бая окрестность этой точки содержит точки, принадлежащие множеству Е, и точки, не принадлежащие этому множеству. Множество Г всех граничных точек множества Е называется границей множества Е.

Множество Е называется открытым множеством, если оно состоит из одних внутренних точек. Множество Е называ­ется связным, если любые две точки этого множества можно соединить непрерывной кривой, состоящей из точек множест­ва Е. Всякое открытое связное множество D на комплексной плоскости называется областью. Область D называется одно­связной, если любую замкнутую кривую в этой области можно непрерывно стянуть в точку, не пересекая границу области. В противном случае область D называется многосвязной.

На рис. 39.2 изображены односвязная область D и много­связная область Ω.

Множество, состоящее из точек области D и ее границы Г, называется замкнутой областью и обозначается 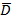.Обход границы Г области D считается положительным, если при дви­жении в этом направлении точки области D остаются слева.

 

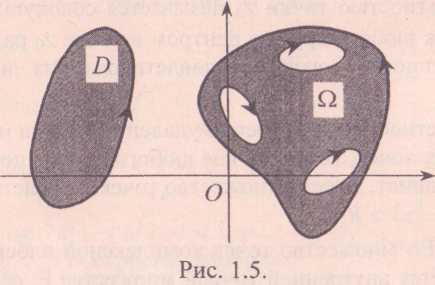
Рис.39.2.

 

На рис.39.2 положительное направление обхода границы Г отмечено стрелками.

Рассмотрим последовательность комплексныхчисел

z₁, z₂,…,z_n,….

Число z₀ называется пределом последовательности {z_n}, если для любой окрестности точки z₀ существует число N такое, что все числа z_n при п >N принадлежат этой окрестности. В этом случае пишут

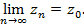
Это определение справедливо и тогда, когда z₀=∞ - бесконеч­но удаленная точка.

Последовательность {z_n} называется сходящейся, если предел z₀ этой последовательности - конечное число.

Пусть z_n = x_n+iy_n,z₀ = x₀+iy₀. Легко доказать, что если последовательность {z_n} имеет конечный предел z₀,то последовательности {х_п} и {у_n} имеют конечные пределы x₀и у₀, и наоборот, если существуют конечные пределы

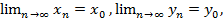то

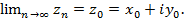
Комплексные функции

Комплексные функции действительного переменного

Если каждому значению действительной переменной t по некоторому закону ставится в соответствие вполне опреде­ленное значение комплексной переменнойz= x+iy,то говорят, что задана комплексная функция z(t). Ясно, что действитель­ная и мнимая части переменной z также являются функциями от t: х= x(t), у = у(t), то есть z(t) = x(t) + iy(t). Задание ком­плексной функции z{t) равносильно заданию двух действи­тельных функций х(t) и y(t).

Пусть задана функция z(t). Тогда каждому значению пе­ременной t на комплексной плоскости соответствует точка z. При изменении t точка z опишет на комплексной плоскости некоторую кривую (L) (рис. 39.3). Уравнение z=z(t) называется комплексно параметрическим уравнением этой кривой. Пара­метрическим уравнением кривой (L) служит система уравне­ний

x = х(t),

y=y(t).

 

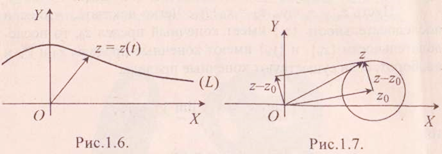
Рис. 39.3 Рис. 39.4

Пример1.: Составить комплексно параметрическое уравне­ние окружности с центром в точке z₀ = x₀+iy₀ радиуса R.

Окружность является геометрическим местом точек, для которых | z-z₀ | = R (рис. 39.4). Таким свойством обладают толь­ко числа, для которых z-z₀ = Re^it. Следовательно, уравнение

z=z₀ + Re^it

является комплексно параметрическим уравнением окружности.

Для комплексных функций действительной перемен­ной естественным образом определяются понятия предела, непрерывности, производной и другие.

Например, если z(t) = x(t)+iy(t), то

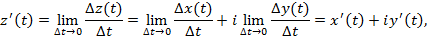
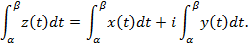
Комплексные функции комплексного переменного

Аналогично определяется понятие комплексной функ­ции комплексного переменного. Если каждому значению ком­плексного переменного z = x+iy по некоторому закону ставится в соответствие вполне определенное значение комплексного переменного w = u+iv, то говорят, что задана комплексная функция комплексного переменного и пишут w = f(z). Дейст­вительная и мнимая части функции f(z) очевидно, являются функциями от z = х + iy, то есть от двух действительных пере­менных х и у: и = и(х,у), v =v(x,y), так что

f(z) = fix,у) + i v(x,y).

Таким образом, задание комплексной функции f(z) от комплекс­ной переменной z равносильно заданию двух действительных функций и(х,у) и v(x,y) от двух действительных переменных хиу. Примерами функций от комплексной переменной являются сте­пенные функции z, z², z³, ..., многочлены P_n(z) = с₀ + c₁z+ ...+c_nzⁿ, дробно-рациональные функции

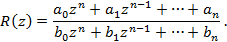
Например, для функции f(z) = z³ имеем

z³ = (x+iy)³ = х³ - Зху² + i(3x²y -у³),

то есть

Ref(z) = f(x,у) = х³ - Зху², Imf(z) = v(x,y) =3x²y -у³.

Каждой действительной функции f(x) действительного пе­ременного х ставится в соответствие некоторая кривая на плос­кости XOY - график этой функции. Такое наглядное представ­ление функций от комплексного переменного невозможно. Вместо этого используется понятие отображения. Для этого рассмотрим две плоскости комплексной переменной: плоскость XOY и плоскость UOV (рис. 39.5).

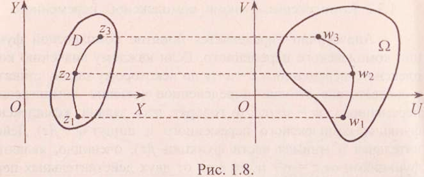
Рис. 39.5

Функция f(z) каждой точке z на плоскости XOY из области определения этой функции ставит в соответствие точку w на плоскости UOV. Точка w называется образом точки г, а точка х - прообразом точки w. Если прообразы z образуют некоторую линию на плоскости XOY, то образы этих точек образуют неко­торую линию на плоскости UOV, если точки z заполняют об­ласть D на плоскости XOY, то их образы образуют некоторую область Ω на плоскости UOV, при этом граничные точки облас­ти D переходят в граничные точки области Ω. Говорят, что функцияf(z) осуществляет отображение области D на область Ω.

Пример 2. Рассмотрим функцию w=l/z. Если z=re^iφ, тоw= (1/r)е'^-iφ. Это означает, что точка w = 1/z лежит на том же луче, выходящем из точки z= 0, что и точка z, на расстоянии 1/r от нача­ла координат (рис. 39.6).

 

 

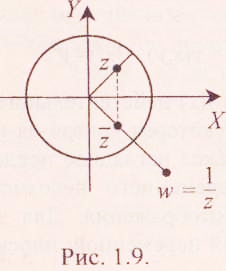
Рис. 39.6

Если | z | = 1, то |w| = 1, то есть единичная ок­ружность на плоскости XOY перехо­дит в единичную окружность на плоскости UOV. Круг |z|<l отобра­жается во внешность круга |w|>l, точка z=0 отображается в точку w=∞, и наоборот, точка z=∞ переходит в точку w=0.

Понятия предела, непрерывности, производной для функ­ций комплексного переменного определяются точно так же, как и для функций действительного переменного. Например, число w₀ называется пределом функции f(z) при z→z₀, если для лю­бого ε>0, как бы мало оно ни было, существует число δ = δ(s) такое, что неравенство |f(z)-w₀ | <ε выполняется для всех z, удовлетворяющих неравенству |z–z₀|<δ, кроме, быть может, точки z₀. В этом случае пишут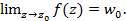

Если z=x+iy, f(z)= f(x,y)+iv(x,y),z₀ = x₀+iy₀, w₀=u₀+iv₀, тосправедливо утверждение: 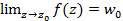тогда и только тогда,когда 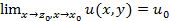и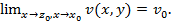

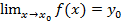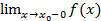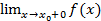Отметим здесь одно важное обстоятельство. Для функций действительного переменного f(x) справедлива теорема: тогда и только тогда, когда оба одностороннихпредела и существуют и равны между собой. Для функций комплексного переменного соответствую­щая теорема формулируется следующим образом.

Предел функции f(z) при z→z₀ существует тогда и только тогда, когда существуют пределы этой функции, если z→z₀по любой кривой L, проходящей через точку z₀,и если все эти пределы равны между собой. Это означает, что существование предела накладывает на функции комплексного переменного более жесткие ограничения, чем на функции действительного переменного.

Далее, функцияf(z) называется непрерывной в точке z₀ ес­ли эта функция определена в точке z₀ и если

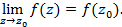
Справедлива следующая теорема: функция f(z)=u(x,y)+iv(x,y) непрерывна в точке z₀ = х₀+iy₀ тогда и только тогда, когда функции u(x,у) и v(x,y) непрерывны в точке 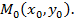Однако как мы увидим в дальнейшем, дифферен­цируемость функци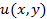й и 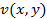не достаточна для диффе­ренцируемости функции 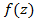. Здесь мы рассмотрели понятие однозначной функции комплексного переменного. В теории функций комплексного переменного рассматриваются также многозначные функции, когда каждому значению комплексного переменного zставится в соответствие не одно, а несколько и даже бесконечно много значений функции 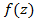.Например, функция 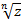каждому 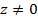ставит в соответствие 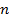различных значений переменной 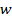, функция Argz при 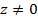принимает бесконечно много значений.

Элементарные функции комплексного переменного

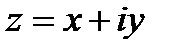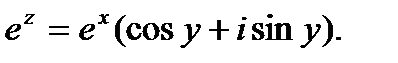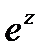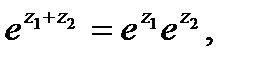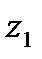Значения показательной функции комплексного переменного вычисляются по формуле Показательная функция обладает следующими свойствами: где и 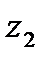- любые комплексные числа; 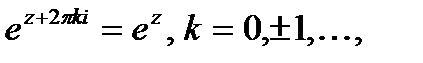т.е. 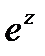является периодической функцией с основным периодом 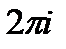. Тригонометрические функции sinz и cosz выражаются через показательную:

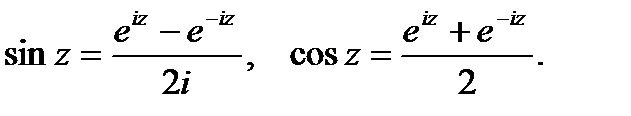
Функци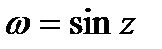и и 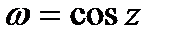- периодические с

Действительным периодом 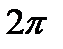и имеют только действительные нул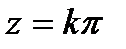и и 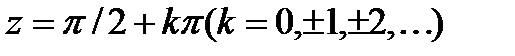соответственно.

Функции tgz и ctgz определяются равенствами

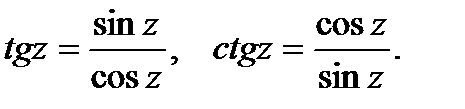
Для тригонометрических функций комплексного переменного остаются в силе все известные формулы тригонометрии.

Гиперболические функции shz, chz, thz, cthz определяются

равенствами

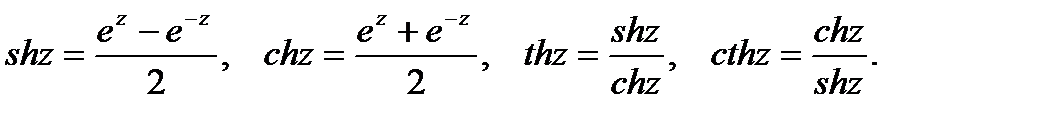
Имеют место тождества shz=-isiniz, chz=cosiz.

Логарифмическая функция Lnz, где 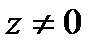, определяется как функция, обратная показательной, причем

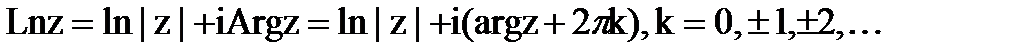
Значение функции, которое получается при k=0, называется

главным значением и обозначается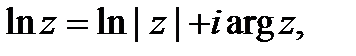

логарифмическая функция обладает следующими свойствами:

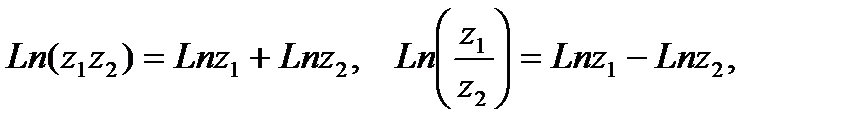
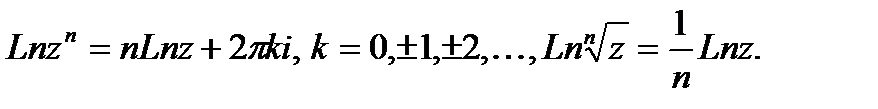
Функции Arcsinz, Arccosz, Arctgz, Arcctgz определяются

как обратные к функциям sinz, cosz, tgz, ctgz соответственно.

Так, если 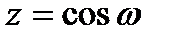, то ω называется арккосинусом числа z и обозначается ω=Arccosz. Все эти функции являются

многозначными и выражаются через логарифмическую:

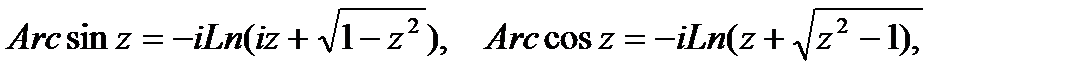
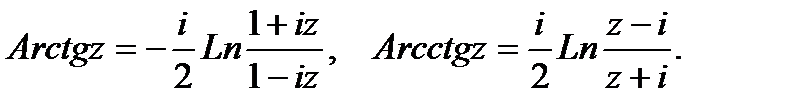
Значения, соответствующие главному значению логарифма, обозначаются темиже символами со строчной буквы (arcsinz, arccosz, arctgz, arcctgz); они называются главными значениями. Общая степенная функция 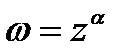, где α—любое

комплексное числе, определяется соотношением 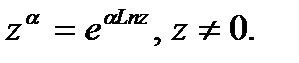Эта функция многозначная; значение 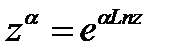называется главным значением. Общая показательная функция 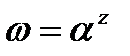, 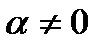определяется равенством 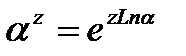. Главное значение этой функции .

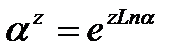Пример 3. Представить в алгебраической форме:

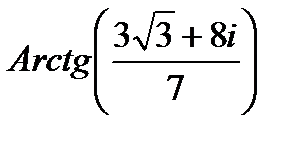
Решение: Функция Arctg является многозначной и в общем виде определяется следующим образом:

Arctg z= -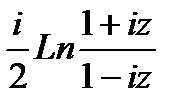

Подставим вместо z значение :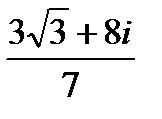

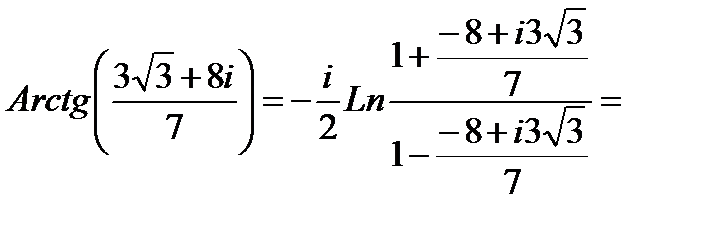
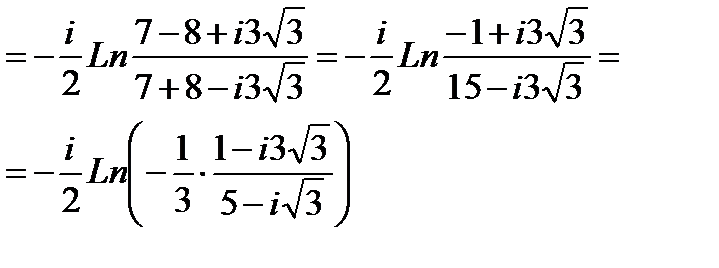
Логарифмическая функция Ln(z), где z 0, определяется как функция, обратная показательной, причем:

,

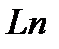
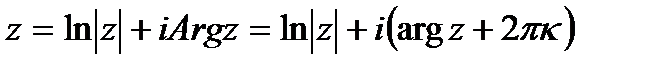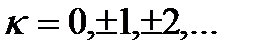
Подставим это выражение в полученное выше:

-

 

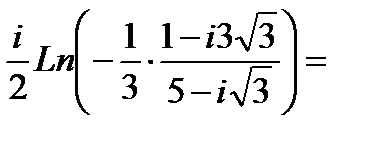
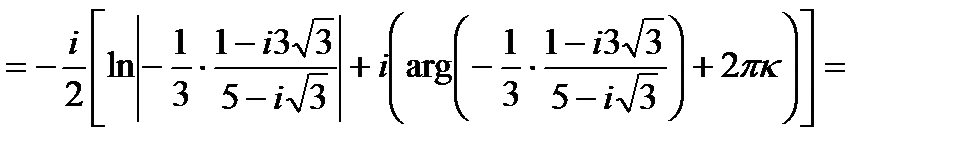
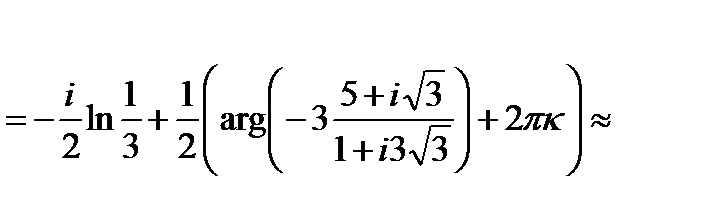
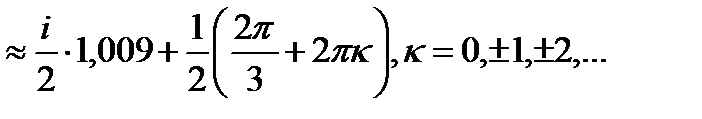
Ответ: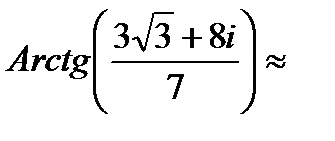

 

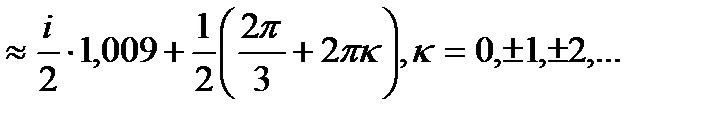
Кривые на комплексной плоскости

Уравнение вида z=z(t)= х(t)+iy(t) определяет на комплексной плоскости кривую, параметрические уравнения которой имеют вид 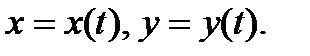Исключением параметра tиз этих уравнений получаем уравнение кривой в виде F (x,у)=0.

Пример 4 . Вычертить область, заданную неравенствами:

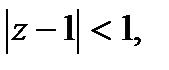
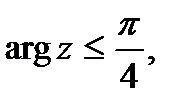
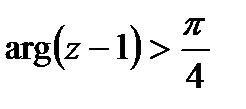
Рис. 39.7

Пример 4 .Определить вид кривой:

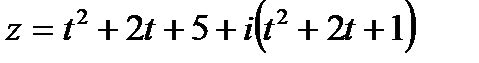
Решение: Уравнение вида 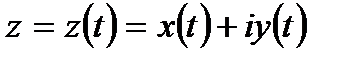определяет на комплексной плоскости кривую, параметрические уравнения которой имеют вид 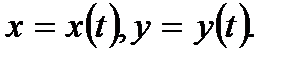В нашем случае:

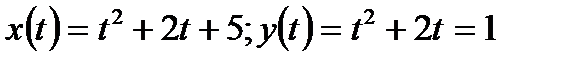
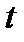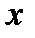Выразим параметр через и :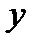

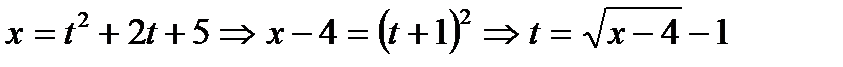
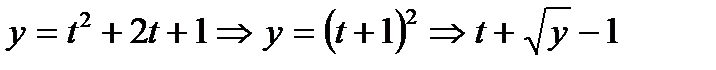
Получим уравнение кривой в виде

.

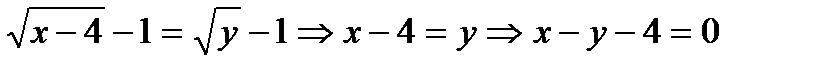ДИФФЕРЕНЦИРОВАНИЕ ФУНКЦИЙ

КОМПЛЕКСНОГО ПЕРЕМЕННОГО,

УСЛОВИЯ КОШИ — РИМАНА

 

Пусть функция определена в некоторой

области Gкомплексного переменного z. Пусть точки zи z+Δz

принадлежат области G. Введем обозначения

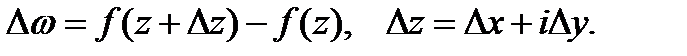
Функция , называется дифференцируемой о точке 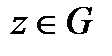, еслиотношение 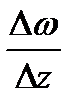имеет конечный предел при 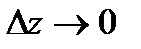. Этот предел называется производной функции

и обозначается , .

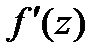
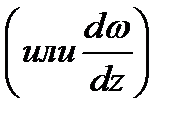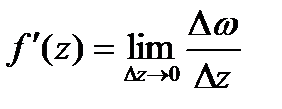Пусть 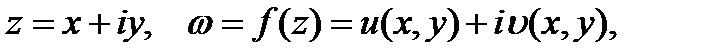, тогда в каждой точке дифференцируемости функции f(z) выполняются соотношения

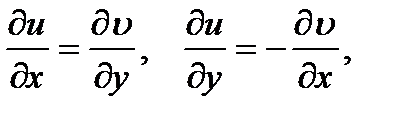(40.1)

называемые условиями Коши — Римана. Обратно, если в некоторой точке (x, у) выполняются условия Коши — Римана и, кроме того, функции и = и(х, у) и υ = υ (х, у) дифференцируемы как функции двух действительных переменных, то функция 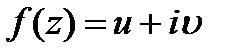является дифферен­цируемой в точке z=x+iy как функция комплексного переменного z. Функция называется аналитической в данной точке z, если она дифференцируема как в самой точке z, так и в некоторой ее окрестности. Функция называется аналитической в области G, если она аналитична в каждой точке 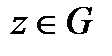.Производная аналитической функции вычисляется по формулам

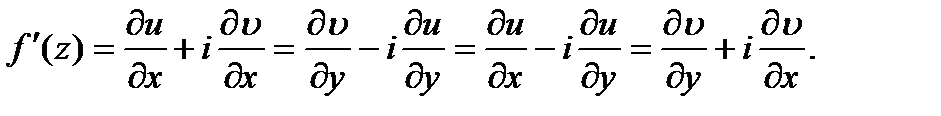
Пользуясь условиями Коши—Римана, можно восстановить

аналитическую функцию , если известна ее

действительная часть 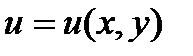или мнимая часть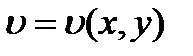

и, кроме того, задано значение 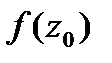функции в некоторой точке 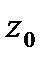. Пусть, например, 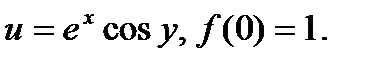Определить аналитическую функцию f(z). В силу условий (40.2) имеем

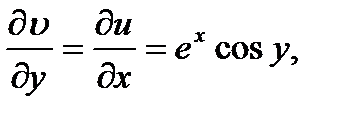(40.3)

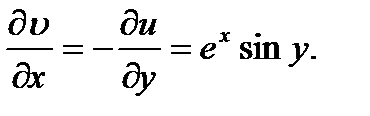(40.4)

Интегрируя уравнение (40.4) по переменной x, находим мнимую часть

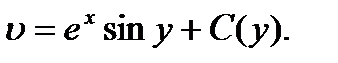(40.5)

Слагаемое С(у) представляет собой постоянную (относительно х)интегрирования. Дифференцируя (40.5) по уи сопоставляя результат c (40.3), получаем 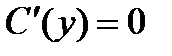,откуда С (у)С. Таким образом, имеем 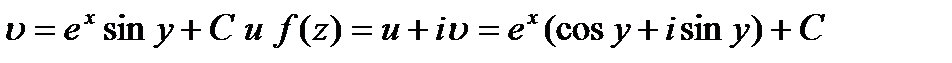с учетом формулы (1) - 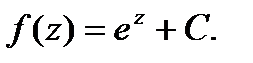Учтем дополнительное

условие f(0) =1, откуда С=0; итак,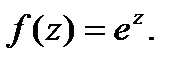

Пример 1.Проверить, что u является действительной частью аналитической функции. Восстановить аналитическую в окрестности точки z₀ функцию f(x) по известной действительной части u (x,y) и значению f (z₀):u = -2xy-2y, f (0) = i

Решение:Зная действительную часть аналитической функции,

можно узнать производную аналитической функции по

следующей формуле: f ^/ (z) = 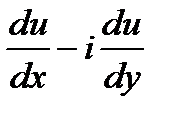. Найдём производную аналитической функции: f ^/ (z) = f ^/ (x + iy) = -2y + 2ix + 2i = 2 (ix – y) + 2i = 2i (x + iy) + 2i= 2iz + 2i. Т.к. производная существует, то u является действительной частью аналитической функции. Зная производную аналитической функции f (z), можно найти производную с точностью до константы: f (z) = 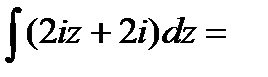iz ² + 2iz +C. Определим константу С: f(0) = i0² + 2i^. 0 + C = i => C = i. Итак, аналитическая функция f (z) выглядит следующим образом: f (z) = iz² +2iz +i

ИНТЕГРИРОВАНИЕ ФУНКЦИЙ

КОМПЛЕКСНОГО ПЕРЕМЕННОГО

Пусть однозначная функция определена и непрерывна в области G,а Г — кусочно-гладкая кривая, лежащая в G;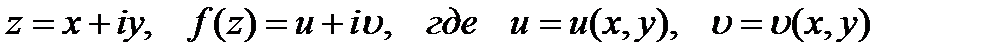

-действительные функции переменных х и у. Вычисление интеграла от функции комплексного переменного zсводится к вычислению криволинейных интегралов по координатам: 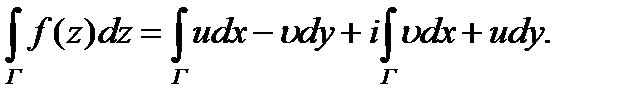Если кривая Г задана параметрическими уравнениями x=x(t), y= y(t), а начальная и конечная точки дуги соответствуют значениям t = α и t=β, то

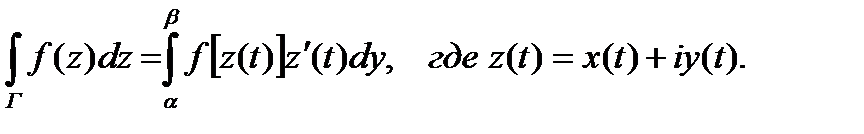
Если — аналитическая функция в односвязной области G, то интеграл не зависит от пути интегрирования (зависит только от начальной и конечной точек). В этом случае для вычисления интеграла применяется формула

Ньютона — Лейбница

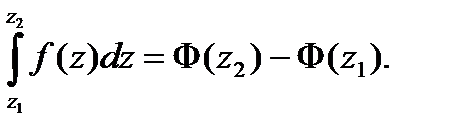где Ф (z) —какая-либо первообразная для функции f(z), т. е, 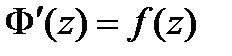в области G, если функция является аналитической в области G, ограниченной кусочно-гладким замкнутым контуром Г, и на самом контуре, то 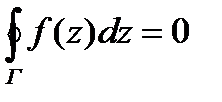(Теорема Коши) и для любой внутренней точки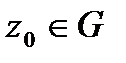 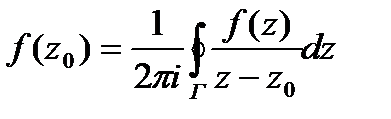(интегральная формула Коши)

Пример 1 .Вычислить интеграл от функции комплексного переменного по данной кривой: 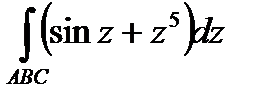; ABC – ломаная: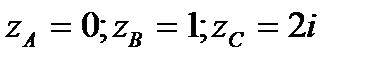

Решение: Покажем кривую, по которой должно проходить

интегрирование:

 

 

Рис. 41.1

Проверим исходную функцию на аналитичность. Для этого перейдем от функции f(z) к функции 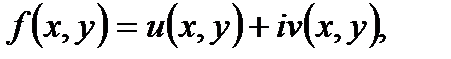где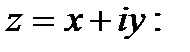

 

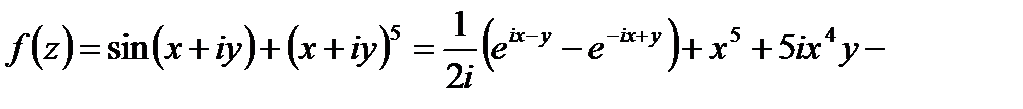
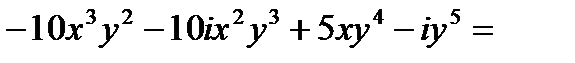
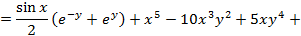
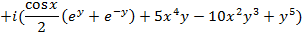
Проверим, выполняются ли условия Коши – Римана:

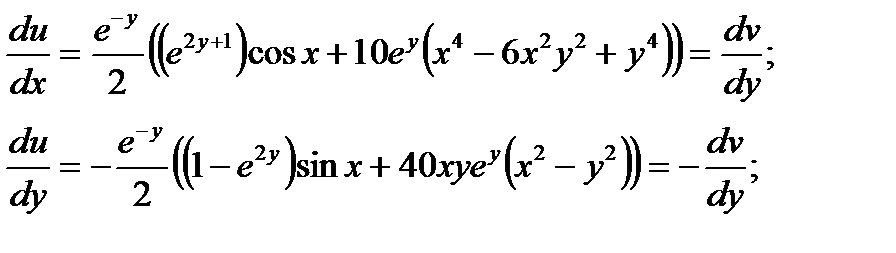
Условия Коши – Римана выполняются, следовательно,

функция является аналитической. Тогда результат от пути интегрирования не зависит: =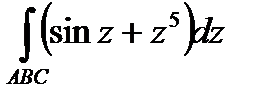

 

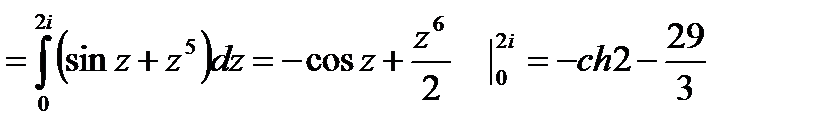
РЯД ЛОРАНА

 

Функция , однозначная н аналитическая в кольце 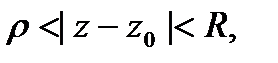разлагается в этом кольце в ряд Лорана

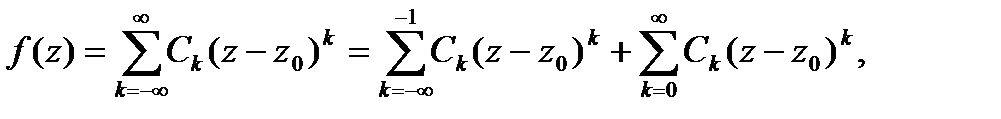(42.1)

коэффициенты находятся по формулам

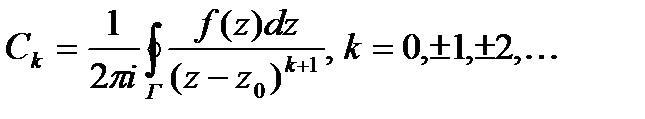(42.2)

Здесь Г—произвольная окружность с центром в точке 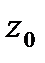,лежащая внутри заданного кольца. Разложение в ряд Лорана единственно. В формуле (42.1) ряды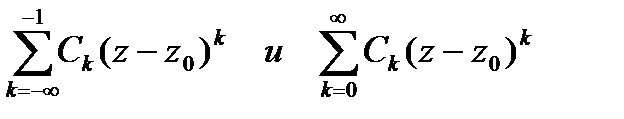

называются соответственно гласной частью ряда Лорана и

правильной частью ряда Лорана. На практике для нахождения коэффициентов 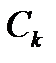, если это возможно, используют готовые разложения элементарных функций в ряд Тейлора. Для примера разложим в ряд Лорана с центром в точке 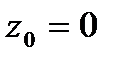функцию 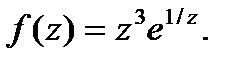Функция 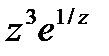аналитична в кольце 0 < | z | < ∞, следовательно, разложима в нем в ряд Лорана. Воспользуемся разложением показательной функции в ряд Тейлора в окрестности точки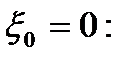 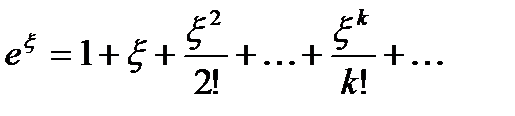и положим 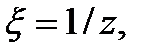тогда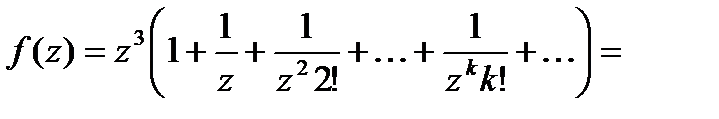

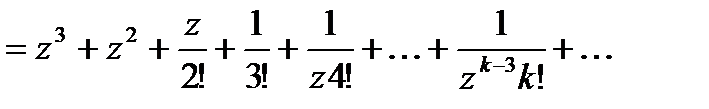
В силу единственности ряда Лорана полученное разложение функции f(z) по степеням zявляется рядом Лорана для функции 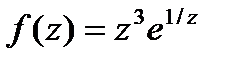в кольце 0 < | z | < ∞.

Пример 1 .Найти все Лорановские разложения данной функции по степеням z.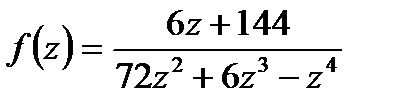

Решение:

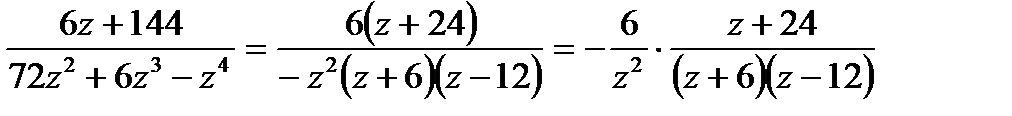
Представим один из множителей, как сумму двух простых слагаемых:

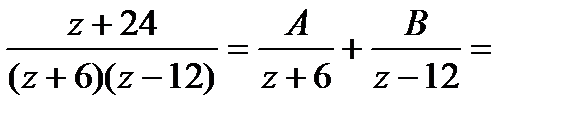
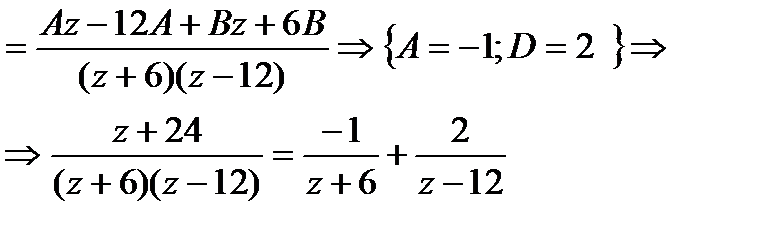.Отсюда f(z) примет вид: f(z)= 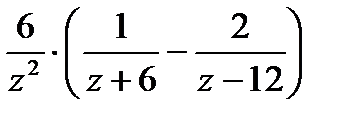. Особые точки: z = 0; z = -6; z = 12

Рис. 42.1

Рассмотрим область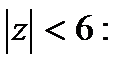

=

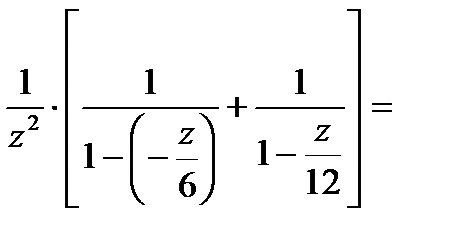
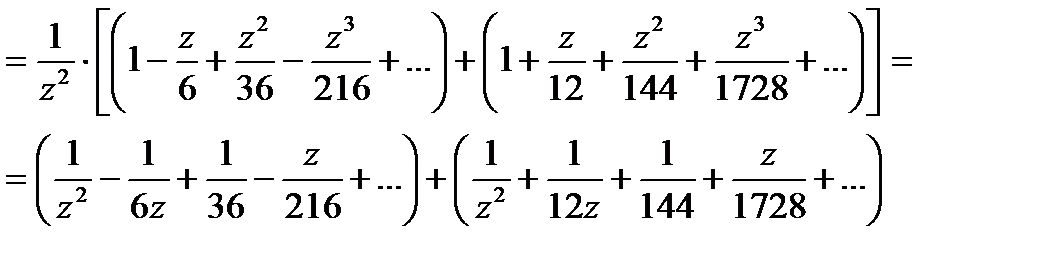
Рассмотрим область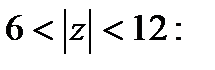

=

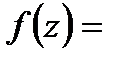
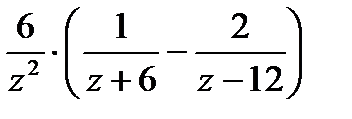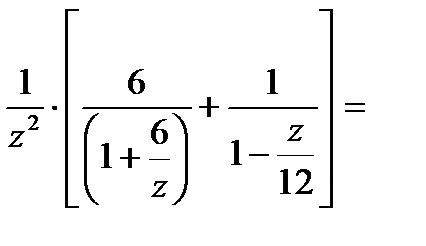
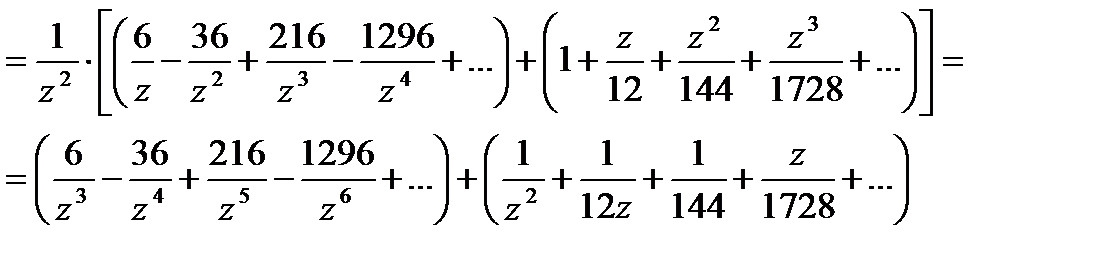
Рассмотрим область =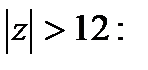

 

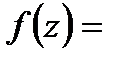
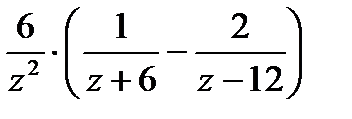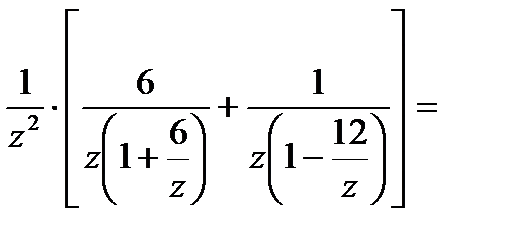
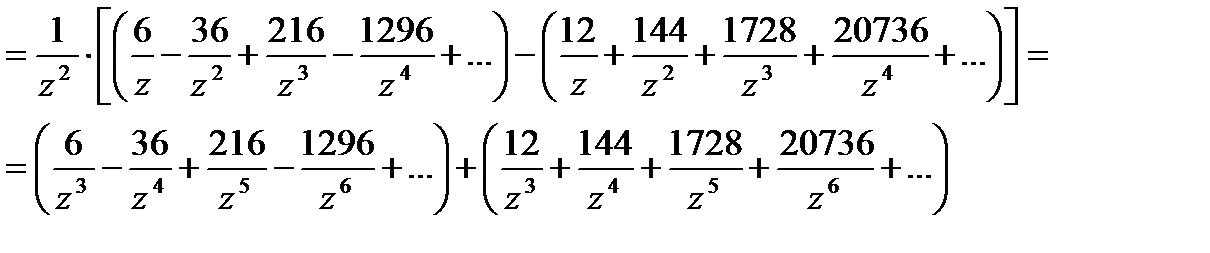
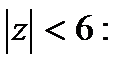
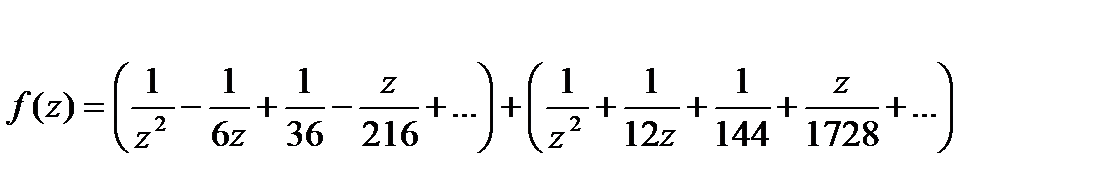
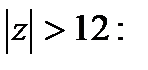
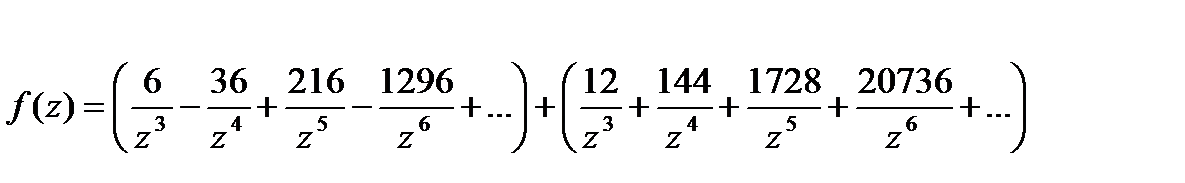
Изолированные особые точки однозначной

аналитической функции

Точка называется изолированной особой точкой функции , если f (z)- однозначная и аналитическая функция в круговом кольце 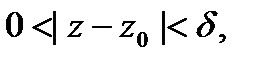кроме самой точки . Функцию вокрестности точки можно разложить вряд Лорана(6), сходящийся в кольце .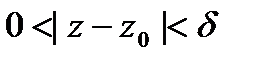

При этом возможны три различных случая, когда ряд Лорана:

1) не содержит членов сотрицательными степенями

разности 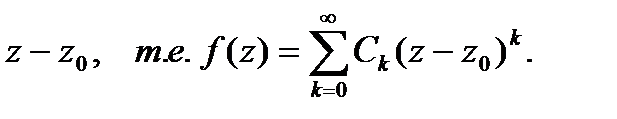В этом случае называется устранимой особой точкой функции ;

2) содержит конечное число членов с отрицательными степенями разности

.

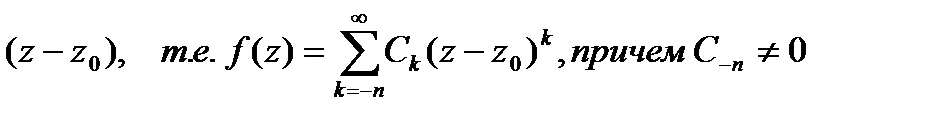В этом случае называется полюсомпорядка n функции ;

3) содержит бесконечное число членов с отрицательными степенями разности

.

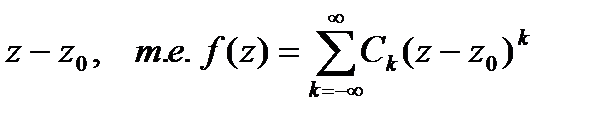В этом случае называется существенно особой точкой функции . При определении характера изолированной особой точки используются следующие утверждения.

1. Для того чтобы точка являлась устранимой особой

точкой аналитической функции , необходимо и достаточно существование предела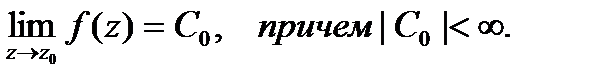

Для того чтобы точка являлась полюсом аналитической

функции , необходимо и достаточно существование

предела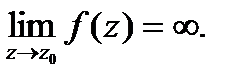

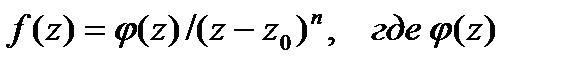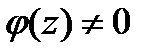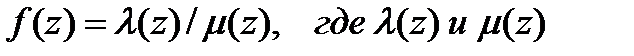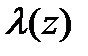2. Для того чтобы точка являлась полюсом порядка п аналитическойфункции f(z),необходимо идостаточно, чтобы функциюf(z)можнобыло представить в виде —функция аналитическая в точке , причем . .Пусть —изолированная особая точка функции —функции аналитические в точке . Если числитель и все производныедо к—1 порядкавключительно в точке равны нулю, 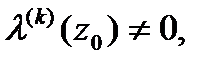знаменатель 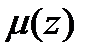и все производныедо l-1 порядка включительно также равны нулю в точке , 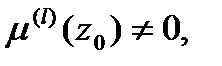то при l>k точка является полюсом порядка n=l—k аналитической функции f(z). (Если 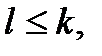то точка является устранимой особойточкой аналитической функции f(z).)В частном случае, при k=0, l = 1 имеем: если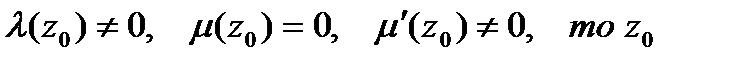— полюс первого порядка функции f(z).

3. Пусть при 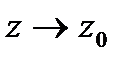аналитическая функция не имеет пределов ни конечного, ни бесконечного. Это условие является необходимым и достаточным для того, чтобы точка была существенно особой точкой функции .

Пример 2 .Для данной функции найти изолированные особые точки и определить их тип.

f (z) = .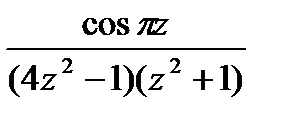

Решение: Изолированными особыми точками являются z = i,

z = -i, z = ½, z = - ½. Запишем данную функцию в виде отношения g (z) и h (z): f (z) = 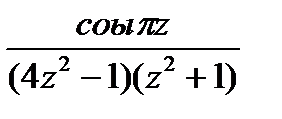;g (z) = cos πz;

h (z) = (4z ² -1)(z ² + 1). Для каждой из функций найдём порядок производной, не обращающейся в ноль при z = i, z = -i, z = ½, z = - ½: g (1/2) = 0, g (-1/2) = 0, g (i) ≠ 0, g (-i) ≠ 0;

g׳(z) = - π sin πz, g ׳ (1/2) ≠ 0, g ׳ (-1/2) ≠ 0; h (1/2) = 0,

h (-1/2) = 0, h (i) = 0, h (-i) = 0; h ׳ (z) = 16z ³ + 6z;

h ׳ (1/2) ≠ 0, h ׳ (-1/2) ≠ 0, h ׳ (i) ≠ 0, h ׳ (-i) ≠ 0.

При z = ½ и z = - ½ порядок ненулевой производной для функции, стоящей в знаменателе, равен порядку ненулевой

производной для функции, стоящей в числителе. Таким образом, можно сделать вывод, что z = ½ и z = - ½ являются

устранимыми особыми точками. Так как порядок производной, не обращающейся в ноль при z = i и z = -i выше для функции, находящейся в знаменателе, то точки z = i и z = -i являются полюсами функции. Порядок этих полюсов находится, как разница между порядками производных, не обращающихся в ноль. В данном случае, это 1 – 0 = 1. Точки z = ½ и z = - ½ являются устранимыми особыми точками. Точки z = i и z = -i являются полюсами 1-го порядка.

Вычеты

Пусть — изолированная особая точка функции . Вычетом функции f (z) в точке называется число, обозначаемое символом 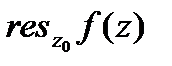и определяемое равенством

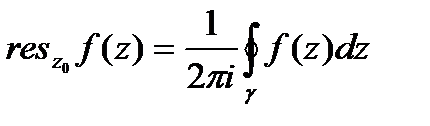(42.3)

(другие обозначения: 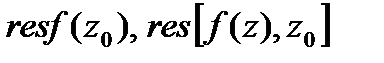). Замкнутый контур интегрирования γ лежит в области аналитичности функции f (z) и не содержит внутри других особых точек функции f (z), кроме . Сопоставление формул (42.1) и (42.3) показывает, что вычет функции равен коэффициенту при минус первой степени в лорановском разложении f (z) в окрестности точки :

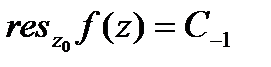. (42.4)

Вычет в устранимой особой точке равен нулю. Вычет функции f (z) в полюсе n-гo порядка вычисляется по формуле

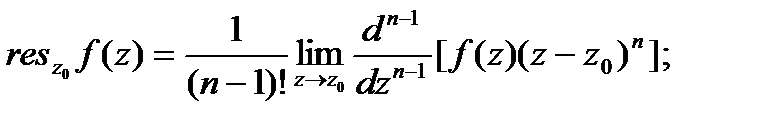
при n=1

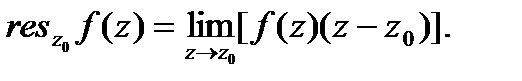
Если функция в окрестности точки представляется как частное двух аналитических функций, 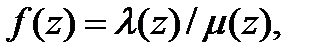причем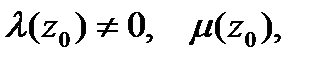 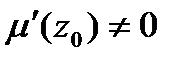(в этом случае — полюс первого порядка функции f (z)), то

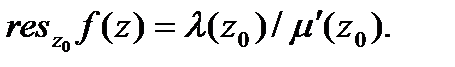
Если точка есть существенно особая точка функции

,то вычет вычисляется по формуле (42.4).

Основная теорема Коши о вычетах.

Если функция