Частные производные первого порядка
Если 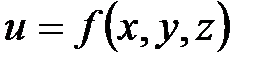 и одна из переменных, например x, получила приращение
и одна из переменных, например x, получила приращение 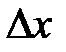 (при постоянных других переменных y и z), то разность
(при постоянных других переменных y и z), то разность 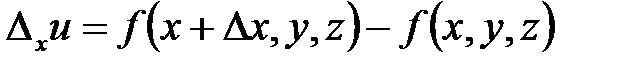 называется частным приращением по
называется частным приращением по 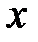 функции
функции 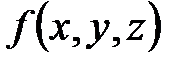 . Соответственно, имеем частные приращения функции по y и по z
. Соответственно, имеем частные приращения функции по y и по z
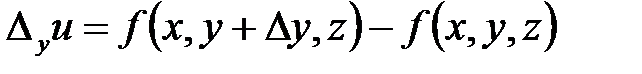 ,
, 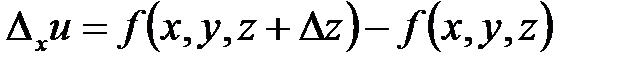
Частной производной от функции 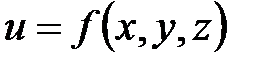 по независимой переменной
по независимой переменной 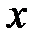 называется производная
называется производная
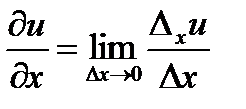 , или в более подробной записи
, или в более подробной записи
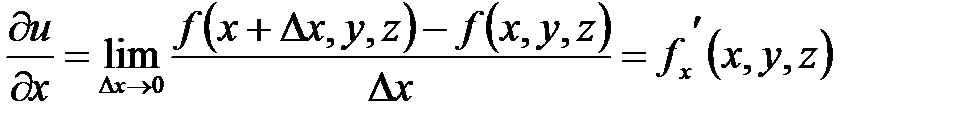 ,
,
вычисленная при постоянных y,z. Обозначается одним из символов 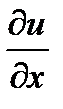 ,
, 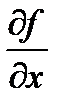 ,
, 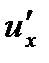 ,
, 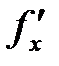 . Аналогично, предел отношения
. Аналогично, предел отношения 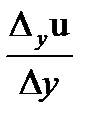 при стремлении
при стремлении 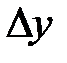 к нулю называется частной производной функции по y:
к нулю называется частной производной функции по y:
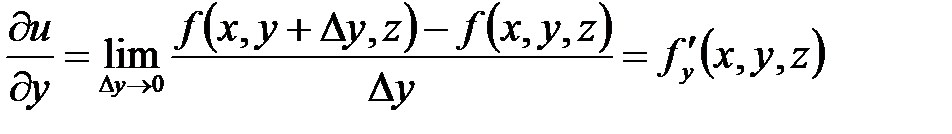 .
.
Частная производная по z есть производная 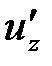 , равная пределу
, равная пределу 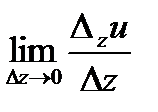 , то есть
, то есть 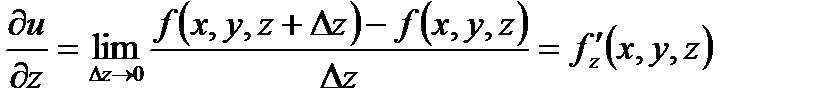 .
.
Очевидно, что для нахождения частных производных справедливы обычные правила и формулы дифференцирования; только следует иметь в виду, что при нахождении частной производной надо считать постоянными все независимые переменные, кроме той, по которой берется частная производная.
Пример 1 .Найти частные производные функции
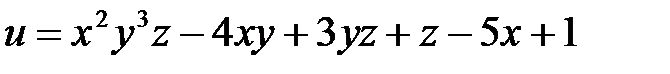 .
.
Решение. Рассматривая переменные  ,
,  как постоянные величины, получим
как постоянные величины, получим 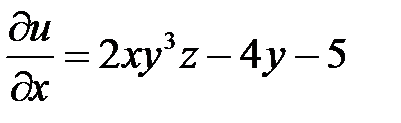 . Считая
. Считая 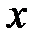 ,
, 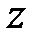 постоянными, дифференцируем функцию по
постоянными, дифференцируем функцию по 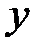 :
:
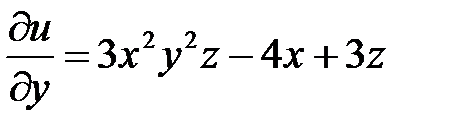 . Аналогично, дифференцируем функцию по z, считая x,y постоянными:
. Аналогично, дифференцируем функцию по z, считая x,y постоянными: 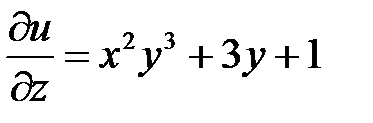 .
.
Полный дифференциал функции.
Полным приращением функции 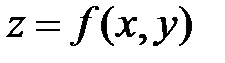 двух независимых переменных в точке M(x,y) называется разность
двух независимых переменных в точке M(x,y) называется разность
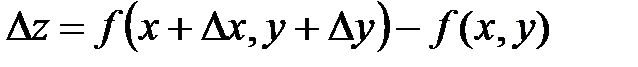 ,
,
где 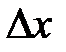 и
и 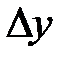 – произвольные приращения аргументов.
– произвольные приращения аргументов.
Функция 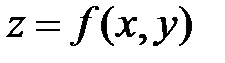 называется дифференцируемой в точке (x,y), если в этой точке полное приращение
называется дифференцируемой в точке (x,y), если в этой точке полное приращение 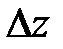 можно представить в виде
можно представить в виде 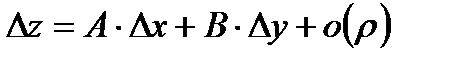 , где слагаемое
, где слагаемое 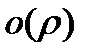 есть бесконечно малая величина высшего порядка по сравнению с бесконечно малой
есть бесконечно малая величина высшего порядка по сравнению с бесконечно малой 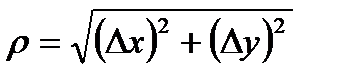 .
.
Полным дифференциалом функции 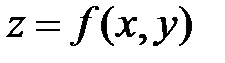 называется главная часть ее полного приращения
называется главная часть ее полного приращения 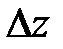 , линейная относительно приращений аргументов
, линейная относительно приращений аргументов 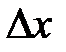 и
и 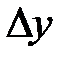 , то есть
, то есть
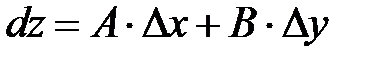 .
.
Дифференциалы dx, dy независимых переменных x и y совпадают с их приращениями, то есть 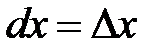 ,
, 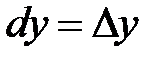 – это числа, равные между собой. Полный дифференциал функции
– это числа, равные между собой. Полный дифференциал функции 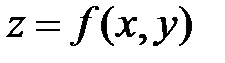 вычисляется по формуле:
вычисляется по формуле:
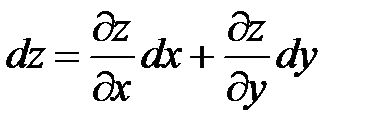 , где
, где 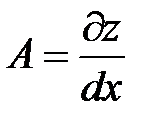 ,
, 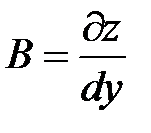
Аналогично, полный дифференциал функции трех аргументов 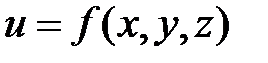 вычисляется по формуле
вычисляется по формуле
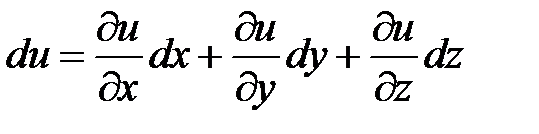
Заметим, что в выражениях 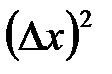 ,
, 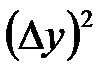 скобки можно опустить, так как
скобки можно опустить, так как 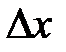 ,
, 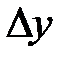 рассматриваются как единый символ. Функция заведомо имеет полный дифференциал в случае непрерывности ее частных производных. Значит, если функция имеет полный дифференциал, то она дифференцируема.
рассматриваются как единый символ. Функция заведомо имеет полный дифференциал в случае непрерывности ее частных производных. Значит, если функция имеет полный дифференциал, то она дифференцируема.
Применения полного дифференциала
к приближенным вычислениям.
Имеем связь между полным дифференциалом функции и ее полным приращением: 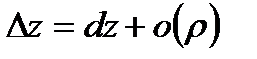 .
.
Вычисление 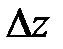 (приращения функции) представляет собой задачу, более трудоемкую, чем вычисление ее дифференциала dz, а потому в практических вычислениях с достаточной точностью при малых приращениях аргументов заменяют вычисление приращения функции вычислением ее дифференциала. При достаточно малых
(приращения функции) представляет собой задачу, более трудоемкую, чем вычисление ее дифференциала dz, а потому в практических вычислениях с достаточной точностью при малых приращениях аргументов заменяют вычисление приращения функции вычислением ее дифференциала. При достаточно малых 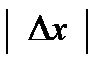 ,
, 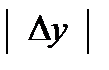 , а значит, при достаточно малом
, а значит, при достаточно малом 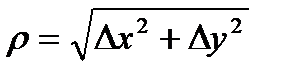 для дифференцируемой функции
для дифференцируемой функции 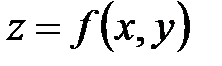 имеет место приближенное равенство
имеет место приближенное равенство
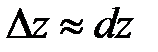 или
или 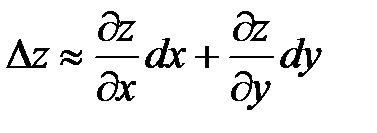 . Итак, получим
. Итак, получим 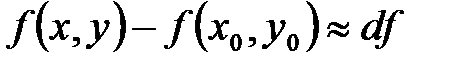 или
или 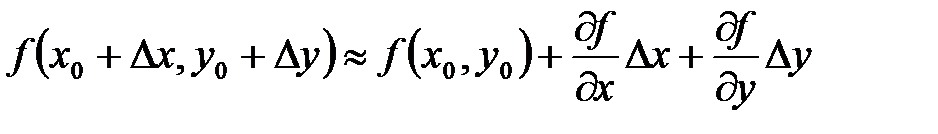 , где
, где 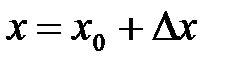 ,
, 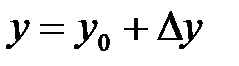 . Это приближенное равенство тем точно, чем меньше величины
. Это приближенное равенство тем точно, чем меньше величины 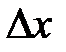 ,
, 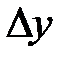 .
.
Пример 2 . Вычислить приближенно величину 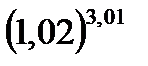
Решение:Рассмотрим функцию 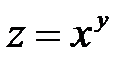 . Воспользуемся формулой. Имеем
. Воспользуемся формулой. Имеем 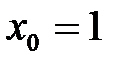 ,
, 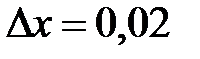 ,
, 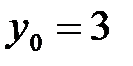 ,
, 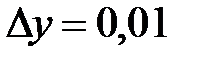 Значение функции
Значение функции 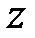 в точке
в точке 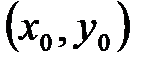 :
: 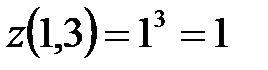 . Вычисляем
. Вычисляем 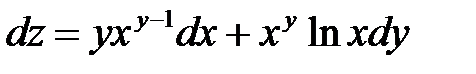 , где
, где 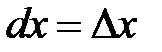 ;
; 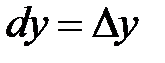 ; откуда
; откуда
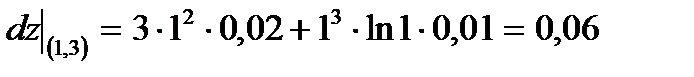 . Значит,
. Значит, 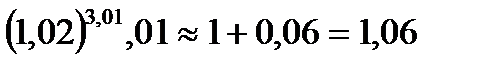 .
.
Дифференцирование сложной функции
1) Случай одной независимой переменной.
Если 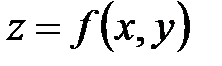 есть дифференцируемая функция двух аргументов x и y в некоторой области D плоскости XOY, которые в свою очередь являются дифференцируемыми функциями независимой переменной t, то есть
есть дифференцируемая функция двух аргументов x и y в некоторой области D плоскости XOY, которые в свою очередь являются дифференцируемыми функциями независимой переменной t, то есть 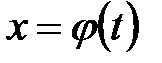 ,
, 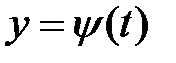 , то сложная функция
, то сложная функция 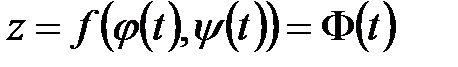 - есть функция одной переменной t и имеет место равенство
- есть функция одной переменной t и имеет место равенство 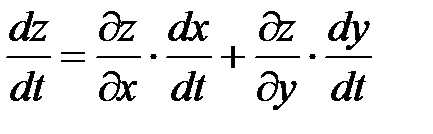 . В частности, если t совпадает с одним из аргументов с x , то справедлива формула
. В частности, если t совпадает с одним из аргументов с x , то справедлива формула 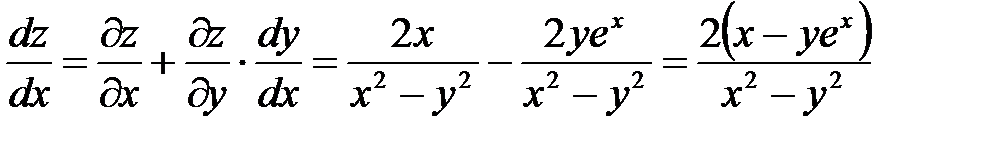 и
и 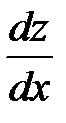 называется полной производной функции z по x.
называется полной производной функции z по x.
Пример 3. Найти 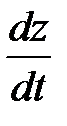 , если
, если 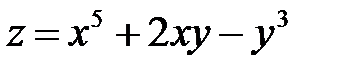 , где
, где 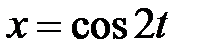 ,
, 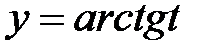 .
.
Решение.Воспользуемся формулой. Предварительно находим
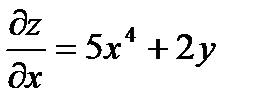 ,
, 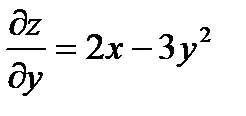 ,
, 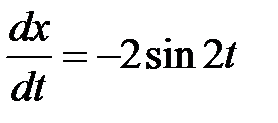 ,
, 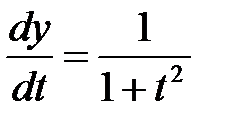 . Тогда
. Тогда 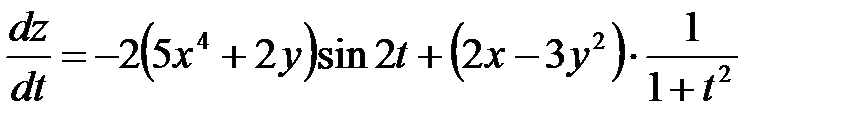
Пример 4 . Найти частную производную 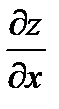 и полную производную
и полную производную 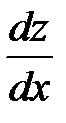 , если
, если 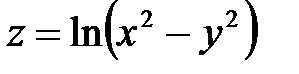 , где
, где 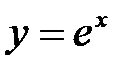 .
.
Решение. Имеем 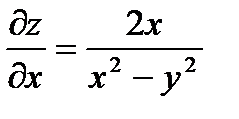 . Находим
. Находим
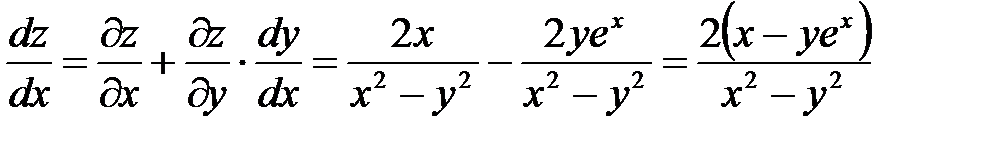
Случай нескольких независимых переменных.
Если z есть сложная функция нескольких переменных, например 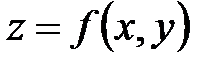 , где аргументы x, y, так называемые промежуточные переменные, являются функциями независимых переменных u, v:
, где аргументы x, y, так называемые промежуточные переменные, являются функциями независимых переменных u, v: 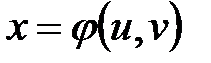 ,
, 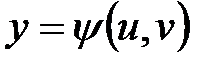 , то сложная функция
, то сложная функция 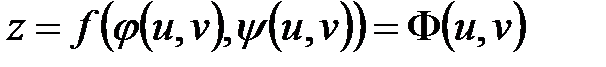 фактически является функцией двух «конечных» переменных u, v. Если функции
фактически является функцией двух «конечных» переменных u, v. Если функции 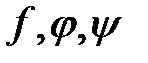 — дифференцируемые функции, то частные производные по
— дифференцируемые функции, то частные производные по 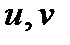 выражаются так:
выражаются так:
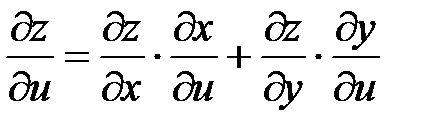 , или
, или 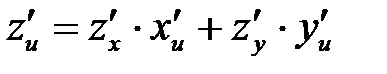
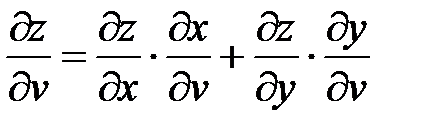 , или
, или 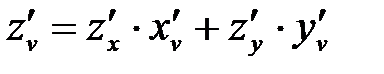
Структура формул та же и при большем числе переменных.
Пример 5 . Найти 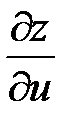 и
и 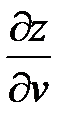 , если
, если 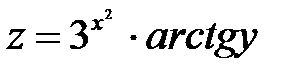 ,
, 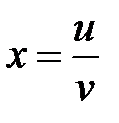 ,
, 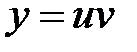
Решение: Находим 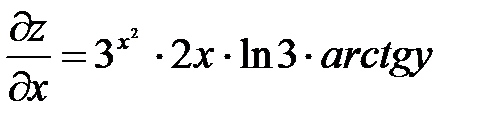 ;
; 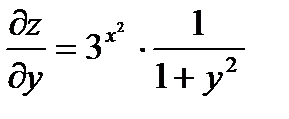 ;
; 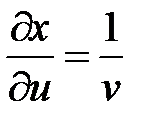 ;
; 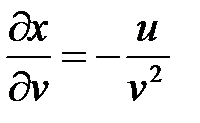 ;
; 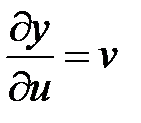 ;
; 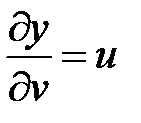 ;
;
Подставляя полученные выражения в формулы, имеем:
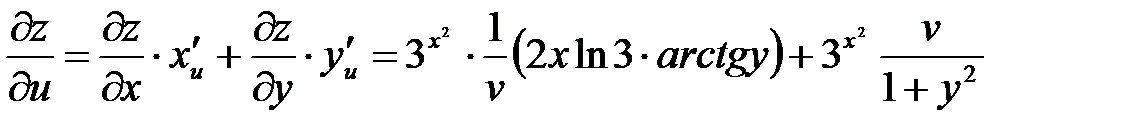 ,
,
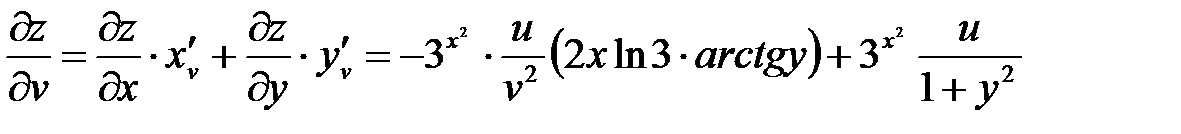 .
.
Ответ можно оставить в такой форме или выразить через u и v. В результате получим: 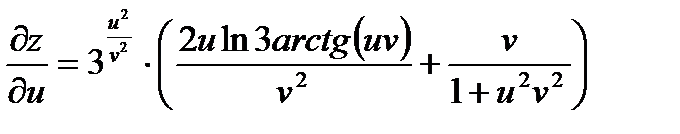 ,
,
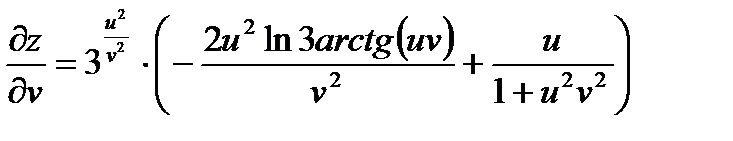 .
.
Инвариантность формы полного дифференциала.
Отметим важное свойство инвариантности формы полного дифференциала. Во всех рассматриваемых выше случаях справедлива формула:
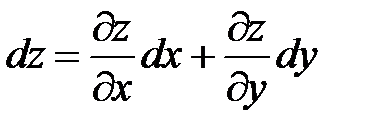 . (*)
. (*)
Действительно, дифференциал сложной функции 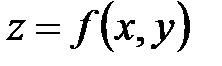 , где переменные
, где переменные 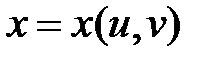 ,
, 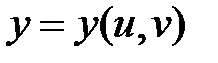 есть функции от новых независимых переменных u и v, можно получить, если в формуле (*) дифференциалы dx и dy заменить (по определению):
есть функции от новых независимых переменных u и v, можно получить, если в формуле (*) дифференциалы dx и dy заменить (по определению):
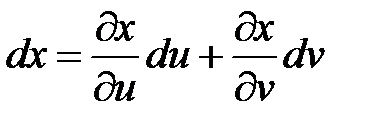 ;
; 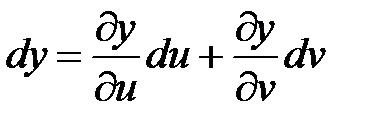 .
.
В результате подстановки и перегруппировки членов при du и dv получим:
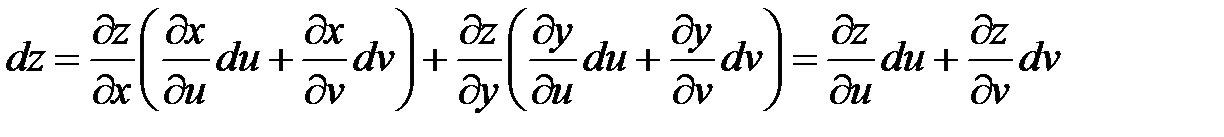 ,
,
где 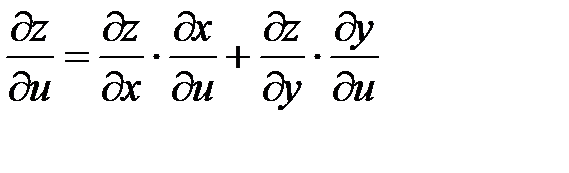 ,
, 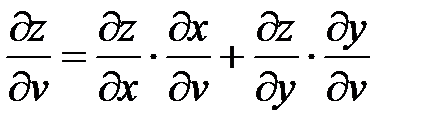 ,
,
полученная формула 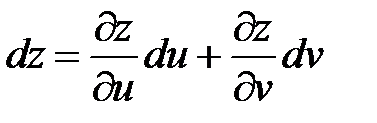 показывает, что форма первого дифференциала не зависит от того, являются ли x и y независимыми переменными или функциями других независимых переменных. Это свойство называется инвариантностью (неизменяемостью) формы первого дифференциала.
показывает, что форма первого дифференциала не зависит от того, являются ли x и y независимыми переменными или функциями других независимых переменных. Это свойство называется инвариантностью (неизменяемостью) формы первого дифференциала.
Производная по направлению.
Градиент функции и его свойство
1. Производной от функции 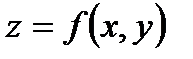 в точке
в точке 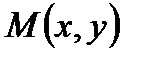 по данному направлению вектора
по данному направлению вектора 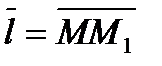 называется
называется 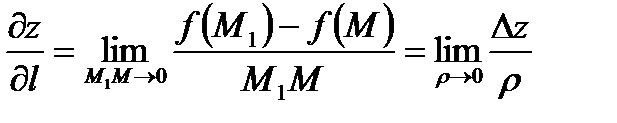 , где
, где 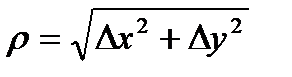 ,
, 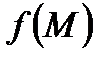 и
и 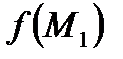 - значения функции в точках М и М1.
- значения функции в точках М и М1.
Если функция 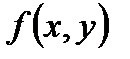 дифференцируема, то производная
дифференцируема, то производная 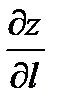 (по направлению
(по направлению 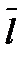 ) вычисляется по формуле:
) вычисляется по формуле: 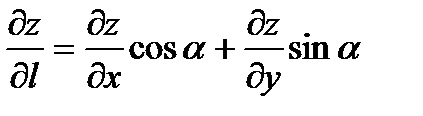 , где α- угол, образованный вектором
, где α- угол, образованный вектором 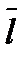 с осью ОХ. В случае функции трёх переменных
с осью ОХ. В случае функции трёх переменных 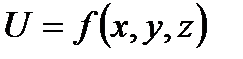 производная по направлению
производная по направлению 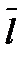 определяется аналогично и вычисляется по формуле
определяется аналогично и вычисляется по формуле 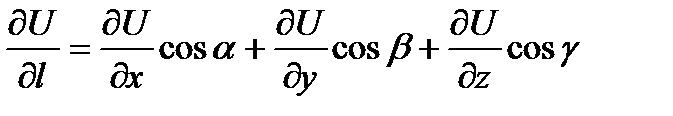 ,
,
где 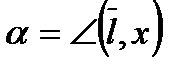 ,
, 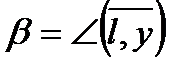 ,
, 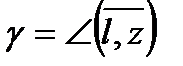 , т.е. α,β,
, т.е. α,β, 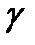 -углы между направлением
-углы между направлением 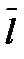 и соответствующими координатными осями, а
и соответствующими координатными осями, а 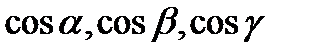 - направляющие косинусы вектора
- направляющие косинусы вектора 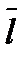 , причём
, причём 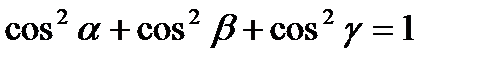 . Производная от функции в данном направлении характеризует скорость изменения функции в этом направлении. Производная
. Производная от функции в данном направлении характеризует скорость изменения функции в этом направлении. Производная 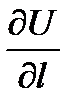 равна нулю по любому направлению, касательному к поверхности уровня .
равна нулю по любому направлению, касательному к поверхности уровня .
Производная 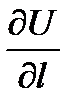 достигает своего наибольшего значения по направлению нормали к поверхности уровня.
достигает своего наибольшего значения по направлению нормали к поверхности уровня.
Пример 6.Найти производную 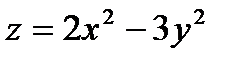 в точке М(1;0) по направлению, составляющему с ОХ угол в
в точке М(1;0) по направлению, составляющему с ОХ угол в 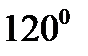 .
.
Решение. Найдём частные производные и их значения в данной точке М: 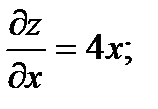
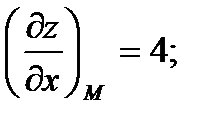
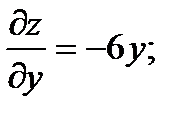
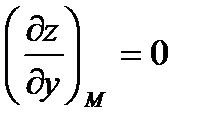 .
.
Далее определяем 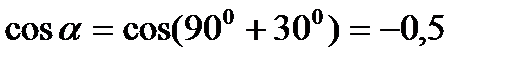 ,
, 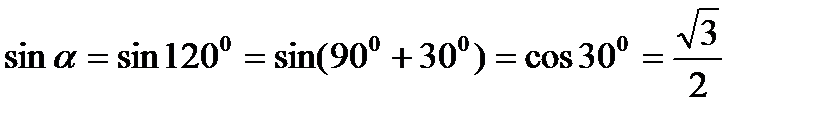 .
.
Получим искомую производную 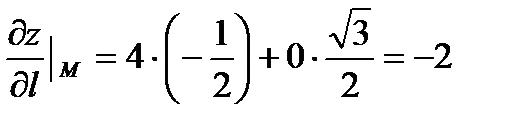 . Знак минус показывает, что функция в данной точке по данному направлению убывает. Известно, что направляющие косинусы вектора
. Знак минус показывает, что функция в данной точке по данному направлению убывает. Известно, что направляющие косинусы вектора 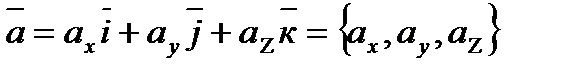 находятся по формулам
находятся по формулам
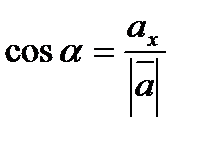 ;
; 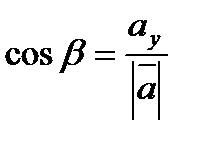 ;
; 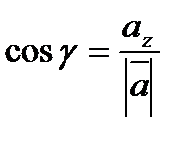 , где
, где 
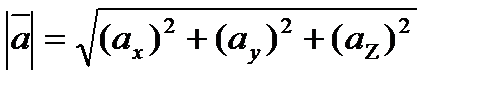
2. Градиентом функции 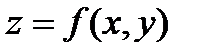 в точке
в точке 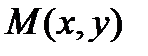 называется вектор, выходящий из точки М и имеющей своими координатами частные производные функции, т.е.
называется вектор, выходящий из точки М и имеющей своими координатами частные производные функции, т.е.
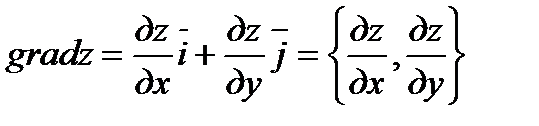 . На основании этого определения проекции вектора
. На основании этого определения проекции вектора 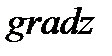 на координатной оси записывается так:
на координатной оси записывается так: 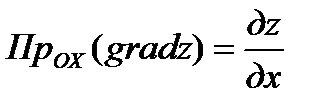 ,
, 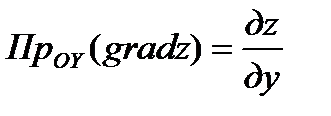 . Предполагается при этом, что функция
. Предполагается при этом, что функция 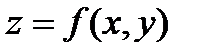 -однозначная непрерывная, имеющая непрерывные частные производные, т.е. дифференцируемая. Значит, производная данной функции в направлении
-однозначная непрерывная, имеющая непрерывные частные производные, т.е. дифференцируемая. Значит, производная данной функции в направлении 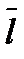 связана с градиентом функции следующей формулой:
связана с градиентом функции следующей формулой: 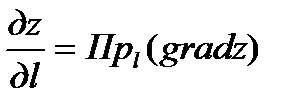 , т.е. производная в данном направлении равна проекции градиента функции на направление дифференцирования. Градиент функции двух переменных в каждой точке направлен по нормали к соответствующей линии уровня функции. Значит направление вектора
, т.е. производная в данном направлении равна проекции градиента функции на направление дифференцирования. Градиент функции двух переменных в каждой точке направлен по нормали к соответствующей линии уровня функции. Значит направление вектора 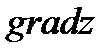 в каждой точке есть направление наибольшей скорости возрастания функции в этой точке, т.е. при
в каждой точке есть направление наибольшей скорости возрастания функции в этой точке, т.е. при 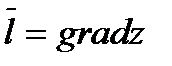 производная
производная 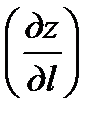 наибольшая
наибольшая
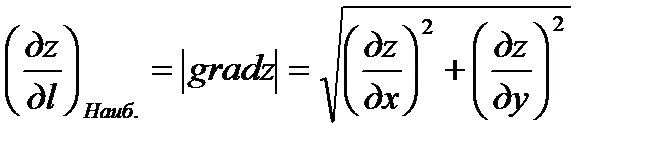 при
при 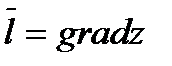 . В этом состоит основное свойство градиента: градиент указывает направление наибольшего роста функции в данной точке. Аналогично определяется градиент функции трёх переменных . Он равен
. В этом состоит основное свойство градиента: градиент указывает направление наибольшего роста функции в данной точке. Аналогично определяется градиент функции трёх переменных . Он равен 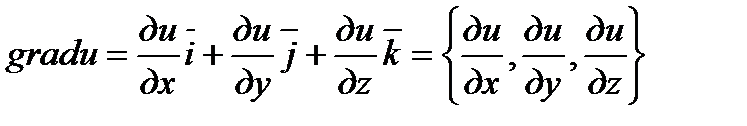 . Градиент функции трёх переменных в каждой точке направлен по нормали к поверхности уровня, проходящей через эту точку.
. Градиент функции трёх переменных в каждой точке направлен по нормали к поверхности уровня, проходящей через эту точку.
Производные и дифференциалы
Высших порядков
Частные производные высших порядков.
Частными производными второго порядка функции 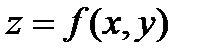 называются частные производные от её частных производных первого порядка.
называются частные производные от её частных производных первого порядка.
Обозначения частных производных второго порядка:
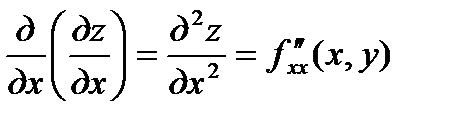 ;
; 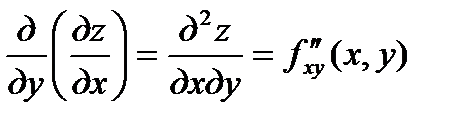 ,
,
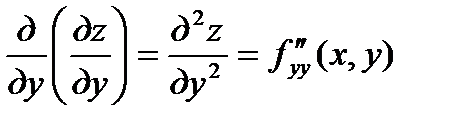 ;
; 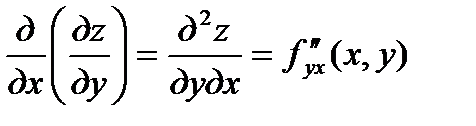 .
.
Аналогично определяются и обозначаются частные производные третьего и выше третьего порядков; например: 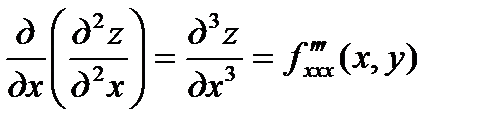 ;
; 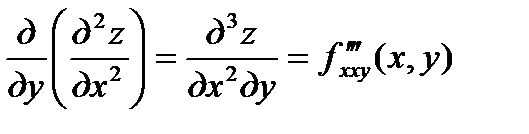 и т.п.
и т.п.
Символ 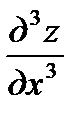 обозначает частную производную третьего порядка функции
обозначает частную производную третьего порядка функции 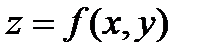 , вычисленную три раза по х; символ
, вычисленную три раза по х; символ 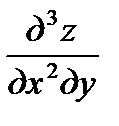 обозначает, что от функции z взята частная производная третьего порядка, причём она вычисляется два раза по х и от полученной производной
обозначает, что от функции z взята частная производная третьего порядка, причём она вычисляется два раза по х и от полученной производной 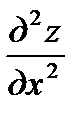 вычислена один раз производная по у. Имеет место такая важная теорема: если частные производные непрерывны, то их значения не зависят от порядка дифференцирования. Таким образом, так называемые смешанные производные, отличающиеся друг от друга лишь последовательностью дифференцирования , равны между собой, если они непрерывные функции, например:
вычислена один раз производная по у. Имеет место такая важная теорема: если частные производные непрерывны, то их значения не зависят от порядка дифференцирования. Таким образом, так называемые смешанные производные, отличающиеся друг от друга лишь последовательностью дифференцирования , равны между собой, если они непрерывные функции, например: 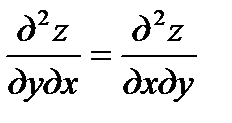 .
.
Пример 1 . Найти частные производные второго порядка от следующих функций: а) z=2xy; б) z=ln(x2+y2); в) 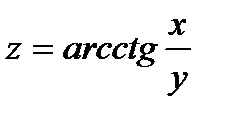 /
/
Решение.Находим сначала частные производные первого порядка. Затем их дифференцируем вторично:
а) 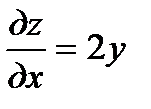 ;
; 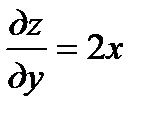 ;
; 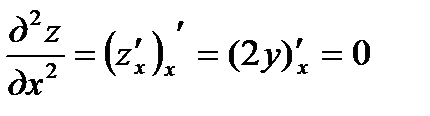 ;
; 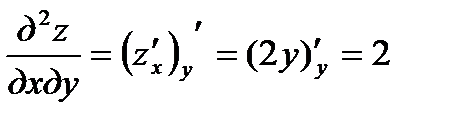 ;
; 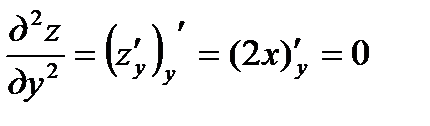 .
.
б) Находим 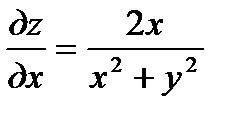 ;
; 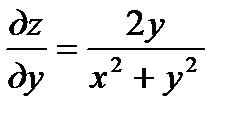 ; далее
; далее
находим 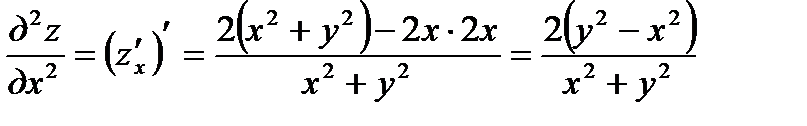 ;
;
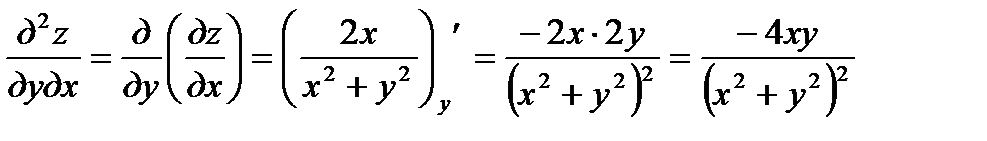 ;
;
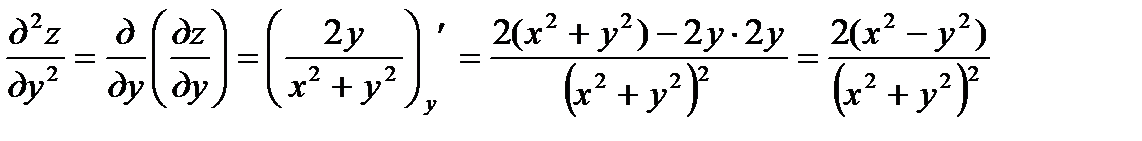 .
.
в) Имеем
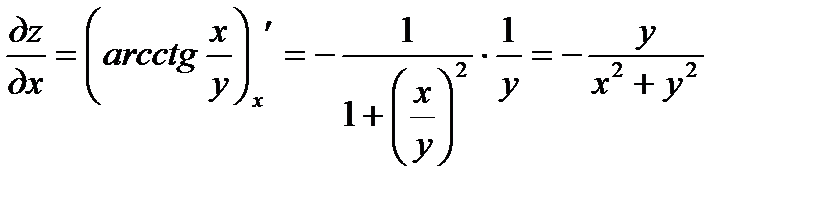 ;
; 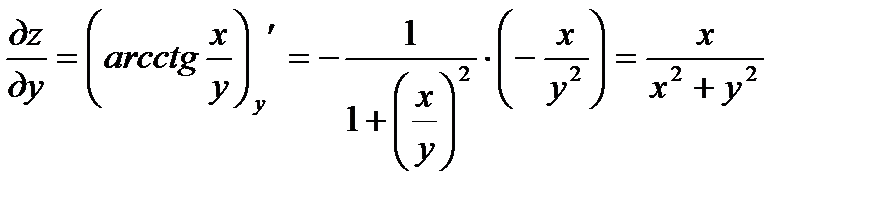 ;
;
Теперь находим: 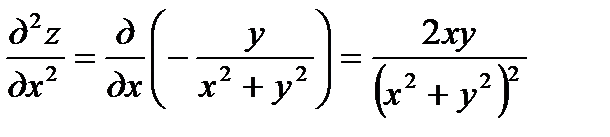 ;
; 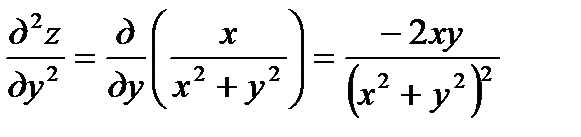 ;
; 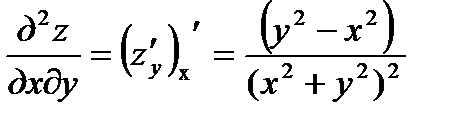 .
.
Дифференциалы высших порядков.
Дифференциалом второго порядка от функции 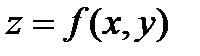 называется дифференциал от её полного дифференциала (первого порядка), т.е.
называется дифференциал от её полного дифференциала (первого порядка), т.е. 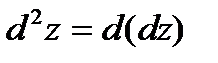 .
.
Аналогично определяются дифференциалы функции z порядка выше второго , например: 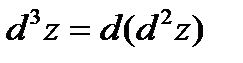 , т.е. дифференциалом третьего порядка от функции z есть дифференциал от её дифференциала второго порядка. Вообще,
, т.е. дифференциалом третьего порядка от функции z есть дифференциал от её дифференциала второго порядка. Вообще, 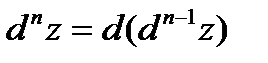 ,
, 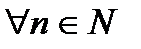 . Если
. Если 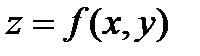 , где аргументы х и у –независимые переменные и функция
, где аргументы х и у –независимые переменные и функция 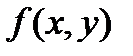 имеет непрерывные частные производные, то дифференциалы высших порядков вычисляются по формулам:
имеет непрерывные частные производные, то дифференциалы высших порядков вычисляются по формулам: 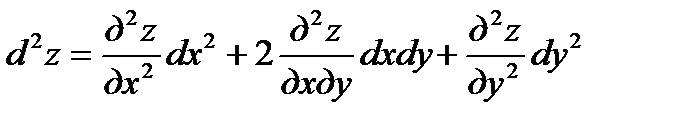
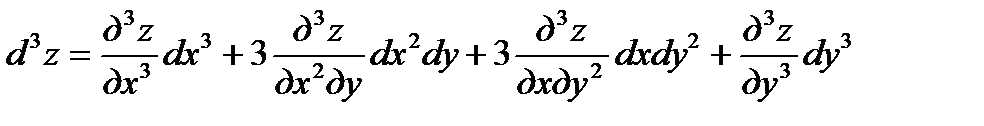 .
.
Вообще, при наличии соответствующих производных справедлива символическая формула для дифференциала порядка n : 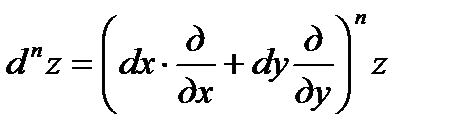 , которая формально раскрывается по биноминальному закону. Если
, которая формально раскрывается по биноминальному закону. Если 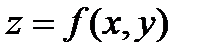 , где аргументы
, где аргументы 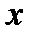 и
и 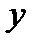 являются функциями одного или нескольких независимых переменных, то
являются функциями одного или нескольких независимых переменных, то 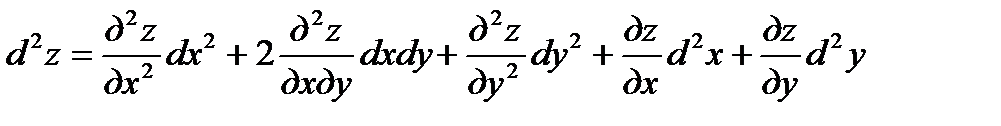
Если х и у – независимые переменные, то 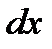 и
и 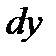 - величины постоянные, поэтому
- величины постоянные, поэтому 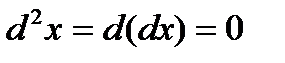 ,
, 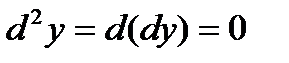 . Заметим, что следующая запись означает
. Заметим, что следующая запись означает 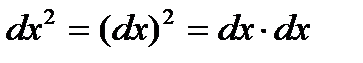 , выражение
, выражение 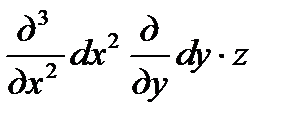 следует понимать, как выражение
следует понимать, как выражение 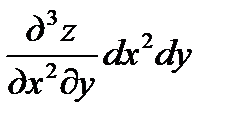 и т.д. Кроме способа вычисления дифференциалов функции по формулам, есть другой способ нахождения дифференциалов высших порядков, который даёт возможность определить их, минуя вычисление частных производных; далее по известному выражению дифференциала мы сможем находить и частные производные. Этот способ состоит в последовательном дифференцировании. Рассмотрим следующий пример.
и т.д. Кроме способа вычисления дифференциалов функции по формулам, есть другой способ нахождения дифференциалов высших порядков, который даёт возможность определить их, минуя вычисление частных производных; далее по известному выражению дифференциала мы сможем находить и частные производные. Этот способ состоит в последовательном дифференцировании. Рассмотрим следующий пример.
Пример 2.Найти дифференциалы первого и второго порядков функции 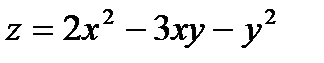 .
.
Решение. Имеем 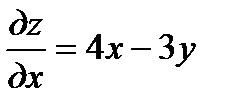 ;
; 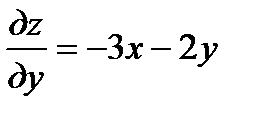 поэтому
поэтому 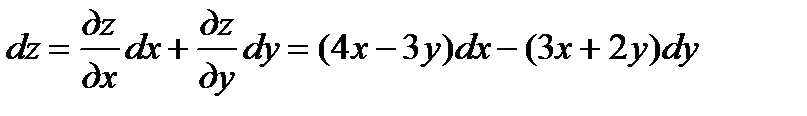 . Далее находим
. Далее находим 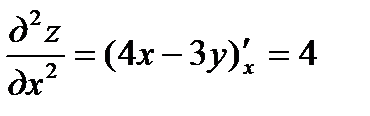 ;
; 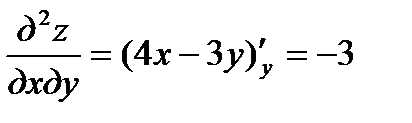 ;
; 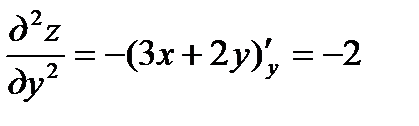 . Имеем:
. Имеем: 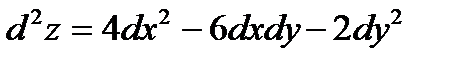 .
.
Дифференцирование неявных функций.
Дата: 2016-10-02, просмотров: 319.