Пусть 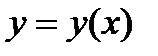 -неявная функция , т.е. она определяется из уравнения
-неявная функция , т.е. она определяется из уравнения 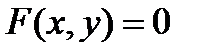 , не разрешённого относительно
, не разрешённого относительно 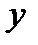 . Это значит, что при каждом значении
. Это значит, что при каждом значении 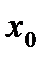 , при котором неявная функция определена, она принимает единственное значение
, при котором неявная функция определена, она принимает единственное значение 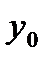 так, что
так, что 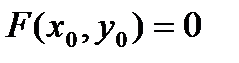 . Если
. Если 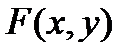 - дифференцируемая функция переменных
- дифференцируемая функция переменных 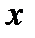 и
и 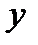 , то производная неявной функции
, то производная неявной функции 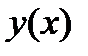 , заданной с помощью уравнения
, заданной с помощью уравнения 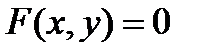 , может быть найдена по формуле
, может быть найдена по формуле 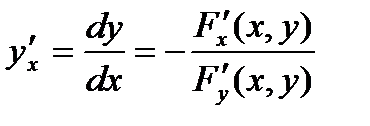 , при условии, что
, при условии, что 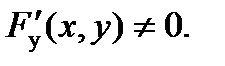 Формула позволяет находить n-ую производную от
Формула позволяет находить n-ую производную от 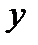 по
по 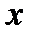 , зная
, зная 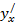 (вычисляя от
(вычисляя от 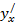 следующие производные).
следующие производные).
Пример 3 . Найти  , если функция
, если функция 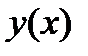 задана неявно уравнением
задана неявно уравнением 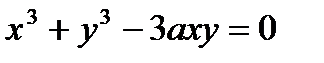 , где
, где 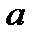 -величина постоянная.
-величина постоянная.
Решение. Обозначим левую часть данного уравнения 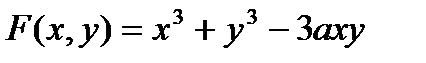 . Найдём её частные производные
. Найдём её частные производные
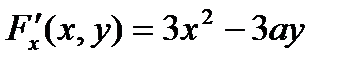 ,
, 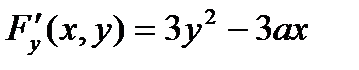 .
.
Применив формулу  , получаем
, получаем 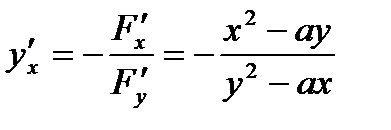 .
.
Случай нескольких независимых переменных.
Если функция z от двух независимых переменных x и y задана уравнением 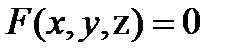 , не разрешённым относительно z, то говорят, что z(x,y) есть неявная функция переменных x и y. Если
, не разрешённым относительно z, то говорят, что z(x,y) есть неявная функция переменных x и y. Если 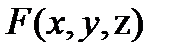 -дифференцируемая функция переменных х , у и z и
-дифференцируемая функция переменных х , у и z и 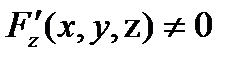 , то частные производные этой неявно заданной функции могут быть найдены по формулам:
, то частные производные этой неявно заданной функции могут быть найдены по формулам:
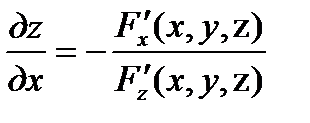 ,
, 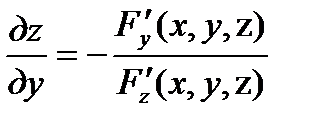 .
.
Существует ещё другой способ нахождения производных от неявно заданной функции z, без использования формулы . Для этого нужно продифференцировать уравнение: 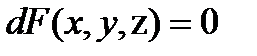 ; считая переменные равноправными
; считая переменные равноправными 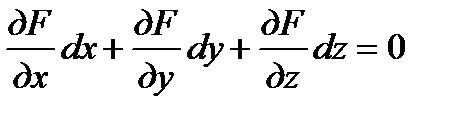 . Из этого уравнения найти
. Из этого уравнения найти 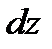 :
: 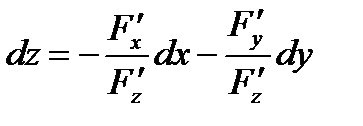 , а следовательно, будем знать
, а следовательно, будем знать 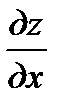 ,
, 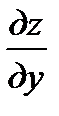 . Чтобы найти вторую производную, например
. Чтобы найти вторую производную, например 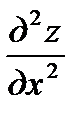 , надо продифференцировать по независимой переменной х найденную первую производную, учитывая при этом, что z есть функция, зависящая от х.
, надо продифференцировать по независимой переменной х найденную первую производную, учитывая при этом, что z есть функция, зависящая от х.
Касательная плоскость и нормаль к поверхности
Касательной плоскостью к поверхности в точке М(точка касания) называется плоскость, содержащая в себе все касательные к различным кривым, проведённым на поверхности через эту точку М.
Нормалью к поверхности называется перпендикуляр к касательной плоскости в точке касания M.
A. Если уравнение поверхности в декартовой системе координат задано в явной форме 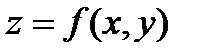 , где
, где 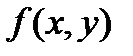 -дифференцируемая функция, то уравнение касательной плоскости в точке М
-дифференцируемая функция, то уравнение касательной плоскости в точке М 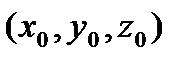 имеет вид
имеет вид 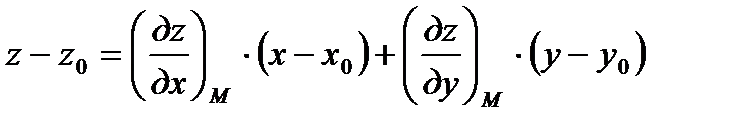 , где
, где 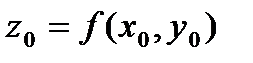 ,
, 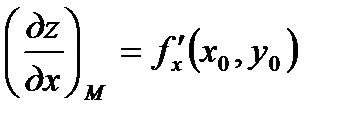 ,
, 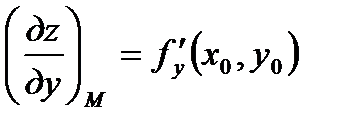 , а
, а 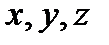 -текущие координаты касательной плоскости, x0,y0,z0 – координаты точки касания М0.
-текущие координаты касательной плоскости, x0,y0,z0 – координаты точки касания М0.
Уравнения нормали к поверхности имеют вид
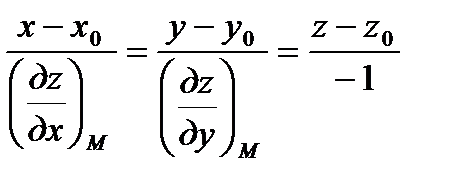
Б. В случае, когда уравнение гладкой поверхности задано в неявной форме 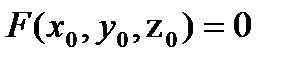 , то уравнение касательной плоскости в точке М
, то уравнение касательной плоскости в точке М 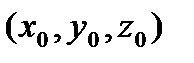 плоскости имеет вид:
плоскости имеет вид: 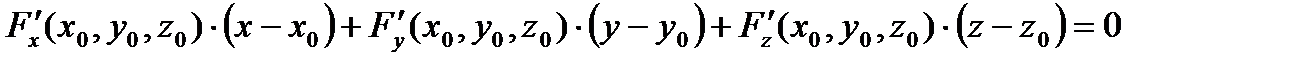 ,
,
Уравнение нормали к поверхности записывается в виде 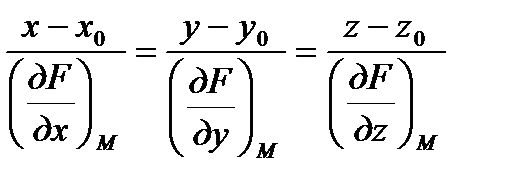 ,
,
где 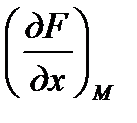 ,
, 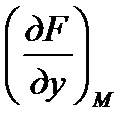 ,
, 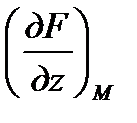 -значения частных производных функции
-значения частных производных функции 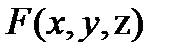 в точке М
в точке М 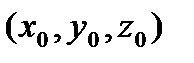 ,x,y,z-текущие координаты касательной плоскости.
,x,y,z-текущие координаты касательной плоскости.
Пример 4. Написать уравнения касательной плоскости и нормали к поверхности 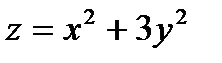 в точке, для которой х=1,у=1.
в точке, для которой х=1,у=1.
Решение. Прежде всего найдём аппликату точки касания 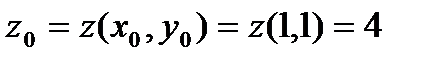 . Итак, точка касания есть М(1,1,4). Находим частные производные данной поверхности, заданной в явной форме:
. Итак, точка касания есть М(1,1,4). Находим частные производные данной поверхности, заданной в явной форме: 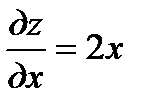 ,
, 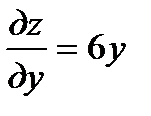 и вычислим их значения в точке М с координатами
и вычислим их значения в точке М с координатами 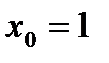 ,
, 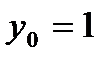 ,
, 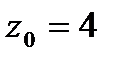 :
: 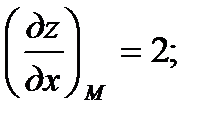
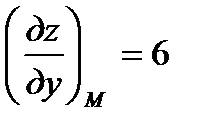 . Будем иметь
. Будем иметь 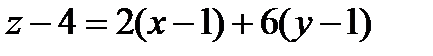 или
или 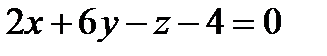 - уравнение касательной плоскости,
- уравнение касательной плоскости, 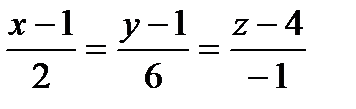 -уравнение нормали.
-уравнение нормали.
Формула Тейлора для функции
Двух переменных
Пусть функция 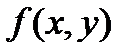 непрерывна вместе со своими частными производными всех порядков до (n+1)-го порядка включительно в окрестности точки (a,b). Тогда в рассматриваемой окрестности справедлива формула Тейлора:
непрерывна вместе со своими частными производными всех порядков до (n+1)-го порядка включительно в окрестности точки (a,b). Тогда в рассматриваемой окрестности справедлива формула Тейлора:
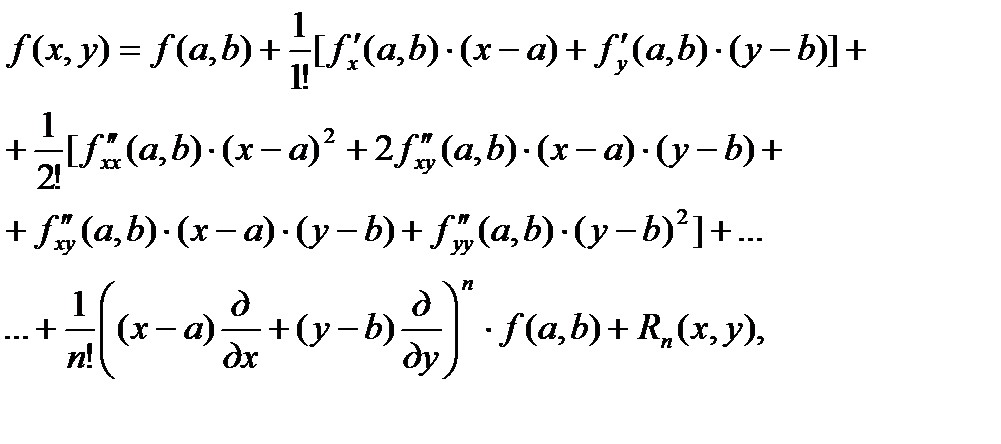
где 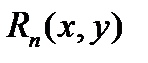 -остаточный член. Формулу Тейлора можно представить в других обозначениях, если обозначить приращение функции в виде
-остаточный член. Формулу Тейлора можно представить в других обозначениях, если обозначить приращение функции в виде 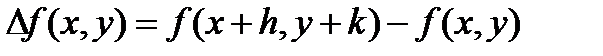 , где h и k-соответствующие приращения аргументов х и у. Тогда
, где h и k-соответствующие приращения аргументов х и у. Тогда
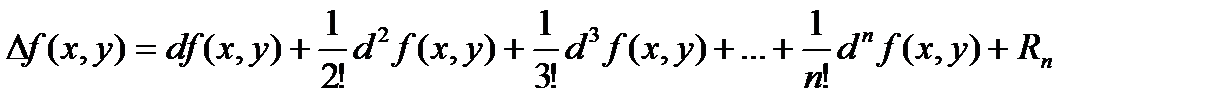 ,
,
где 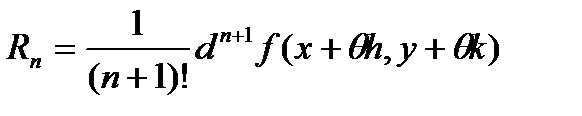 ,
, 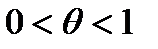 . Частный случай формулы Тейлора при a=b=0 называется формулой Маклорена.
. Частный случай формулы Тейлора при a=b=0 называется формулой Маклорена.
Экстремум функции нескольких
Независимых переменных
Основные теоретические сведения.
Говорят, что функция 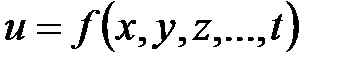 при некоторой системе значений
при некоторой системе значений 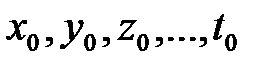 независимых переменных имеет максимум (минимум), если приращение функции
независимых переменных имеет максимум (минимум), если приращение функции
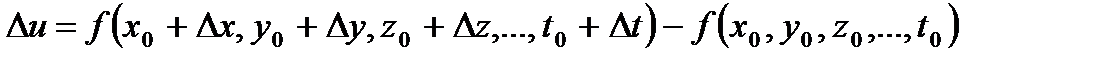
отрицательно (положительно) при всевозможных, достаточно малых по абсолютной величине как положительных, так и отрицательных значениях приращений аргументов
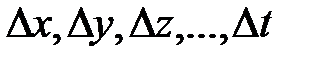 . Максимум или минимум функции называется экстремумом. Экстремум здесь понимается в локальном смысле. Точка, в которой достигается экстремум, называется точкой экстремума. Для функции двух переменных
. Максимум или минимум функции называется экстремумом. Экстремум здесь понимается в локальном смысле. Точка, в которой достигается экстремум, называется точкой экстремума. Для функции двух переменных 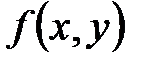 удобно определение локального экстремума следующее:
удобно определение локального экстремума следующее:
Определение. Функция 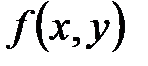 имеет максимум (минимум) в точке
имеет максимум (минимум) в точке 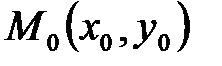 , если значение функции в этой точке больше (меньше), чем ее значение в любой другой точке
, если значение функции в этой точке больше (меньше), чем ее значение в любой другой точке 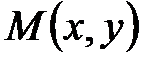 в достаточно малой окрестности точки
в достаточно малой окрестности точки 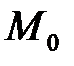 , то есть,
, то есть, 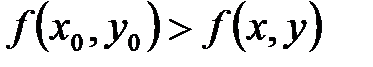 (или соответственно
(или соответственно 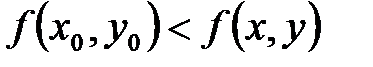 ) для всех точек
) для всех точек 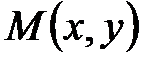 , удовлетворяющих условию
, удовлетворяющих условию 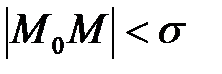 , где
, где 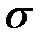 – достаточно малое положительное число. Аналогично определение экстремума функции трех и большего числа переменных, используя понятие многомерного пространства.
– достаточно малое положительное число. Аналогично определение экстремума функции трех и большего числа переменных, используя понятие многомерного пространства.
Необходимые условия экстремума.
Если дифференцируемая функция 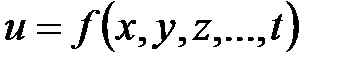 достигает экстремума в точке
достигает экстремума в точке 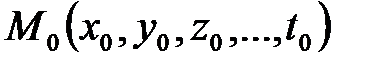 , то или ее частные производные первого порядка в этой точке равны нулю
, то или ее частные производные первого порядка в этой точке равны нулю
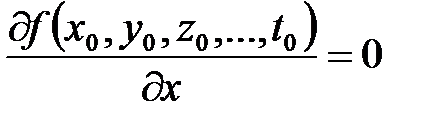 ;
; 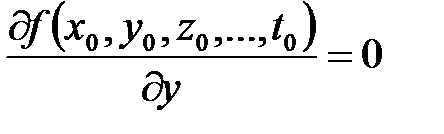 ;
; 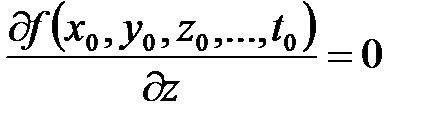 ; … ;
; … ; 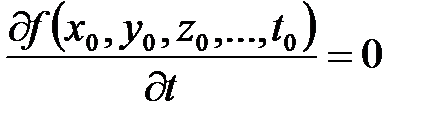
или частные производные при этих значениях не существуют.
Система равенств эквивалентна одному уравнению:
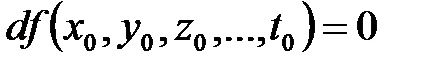 ,
,
Итак, в точке экстремума первый дифференциал функции равен нулю или не существует. Количество уравнений в системе равно числу независимых переменных. Точки, в которых вычисляются равенства , называются стационарными (или критическими) точками. Эти точки являются только подозрительными на экстремум, так как не всякая стационарная точка является точкой экстремума. Поэтому, равенства выражают необходимое, но недостаточное условие экстремума функции нескольких переменных.
Достаточные условия экстремума.
Для того, чтобы решить вопрос, какие стационарные точки, получаемые из решения системы уравнений:
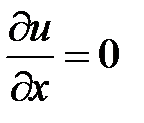 ;
; 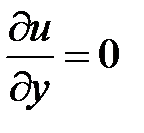 ;
; 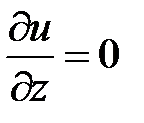 ;…;
;…; 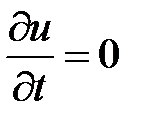 , доставляют функции максимум или минимум, или ни то, ни другое, обращаются к исследованию дифференциала второго порядка этой функции. Пусть
, доставляют функции максимум или минимум, или ни то, ни другое, обращаются к исследованию дифференциала второго порядка этой функции. Пусть 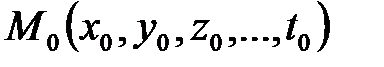 - стационарная точка функции
- стационарная точка функции 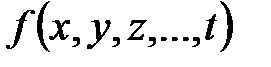 ,. Тогда если дифференциал второго порядка сохраняет постоянный знак при всевозможных достаточно малых по модулю приращениях аргументов, то функция в точке
,. Тогда если дифференциал второго порядка сохраняет постоянный знак при всевозможных достаточно малых по модулю приращениях аргументов, то функция в точке 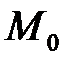 имеет экстремум, причем максимум будет в том случае, когда
имеет экстремум, причем максимум будет в том случае, когда 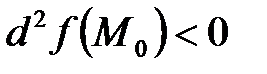 , а минимум – когда
, а минимум – когда 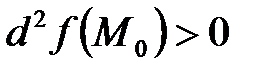 . Если дифференциал второго порядка
. Если дифференциал второго порядка 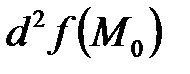 не сохраняет постоянного знака, то функция в точке
не сохраняет постоянного знака, то функция в точке 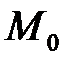 не имеет ни максимума, ни минимума. Если же
не имеет ни максимума, ни минимума. Если же 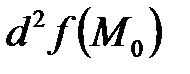 обратится в нуль, то решение вопроса об экстремуме требует исследования дифференциалов порядка выше, чем второй.
обратится в нуль, то решение вопроса об экстремуме требует исследования дифференциалов порядка выше, чем второй.
Правило определения экстремума функции
двух независимых переменных.
Чтобы исследовать на экстремумы функцию 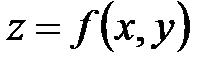 двух независимых переменных x, y, следует:
двух независимых переменных x, y, следует:
1) Определить стационарные точки, в которых функция может достигать экстремума.
2) Для этого надо решить систему уравнений 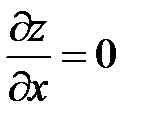 ;
; 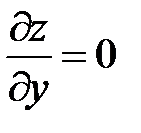 (необходимые условия экстремума)
(необходимые условия экстремума)
2) Найти частные производные второго порядка 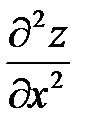 ;
; 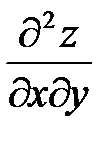 ;
; 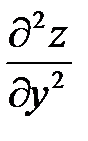 и вычислить значения вторых частных производных в каждой стационарной точке. Достаточные условия экстремума выражаются с помощью определителя второго порядка. Например, пусть
и вычислить значения вторых частных производных в каждой стационарной точке. Достаточные условия экстремума выражаются с помощью определителя второго порядка. Например, пусть 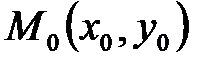 - найденная стационарная точка данной функции. Принято обозначать числа следующими буквами
- найденная стационарная точка данной функции. Принято обозначать числа следующими буквами
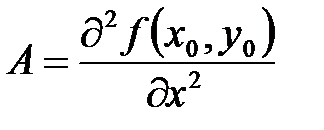 ;
; 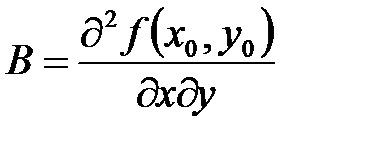 ;
; 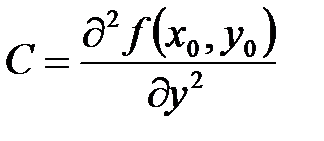 .
.
3) Составить определитель 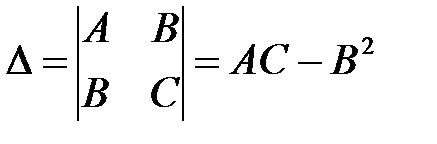 для каждой стационарной точки. При этом,
для каждой стационарной точки. При этом,
а) если 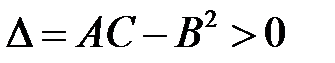 то экстремум в стационарной точке есть: при A>0 (или C>0) будет минимум, а при A<0 (или С<0) будет максимум;
то экстремум в стационарной точке есть: при A>0 (или C>0) будет минимум, а при A<0 (или С<0) будет максимум;
б) если 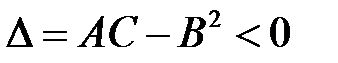 , то экстремума в рассматриваемой стационарной точке нет;
, то экстремума в рассматриваемой стационарной точке нет;
в) если 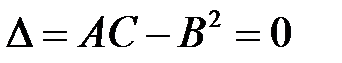 , то вопрос о наличии или отсутствии экстремума функции в стационарной точке остается открытым (требуется дальнейшее исследование функции с привлечением частных производных порядка выше второго, или, например, по знаку приращения
, то вопрос о наличии или отсутствии экстремума функции в стационарной точке остается открытым (требуется дальнейшее исследование функции с привлечением частных производных порядка выше второго, или, например, по знаку приращения 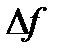 вблизи этой точки).
вблизи этой точки).
Пример 1 . Исследовать на экстремум функцию
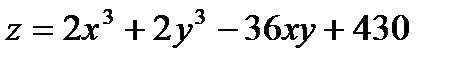
Решение: 1) Найдем частные производные первого порядка
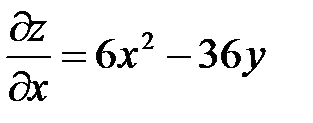 ;
; 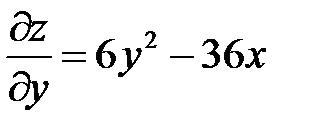
Воспользуемся необходимым условием экстремума:
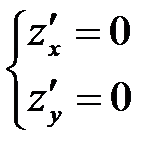 ; составляем систему уравнений
; составляем систему уравнений 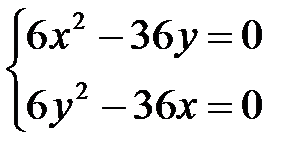 .
.
После сокращения на 6 имеем 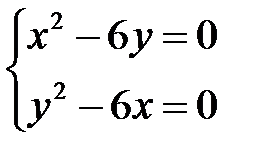 . Решаем систему. Из первого уравнения находим
. Решаем систему. Из первого уравнения находим 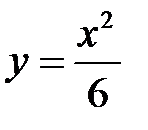 , подставляя его во второе уравнение, получим
, подставляя его во второе уравнение, получим 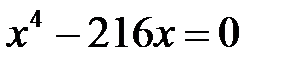 , или
, или 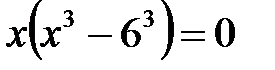 , или
, или 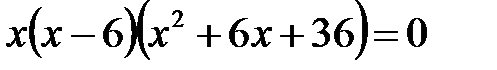 .Откуда имеем
.Откуда имеем 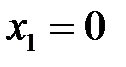 ;
; 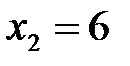 (остальные два корня уравнения
(остальные два корня уравнения 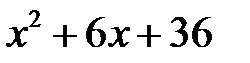 будут комплексными, нас они не интересуют); далее из уравнения
будут комплексными, нас они не интересуют); далее из уравнения 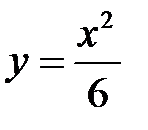 находим
находим 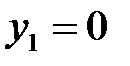 при
при 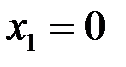 и
и 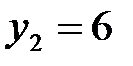 при
при 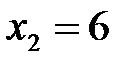 . Итак, получим две стационарные точки
. Итак, получим две стационарные точки 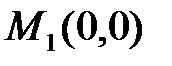 ,
, 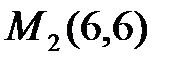
2) Для исследования достаточных условий экстремума нашли частные производные второго порядка 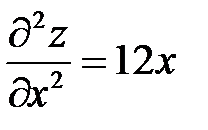 ;
; 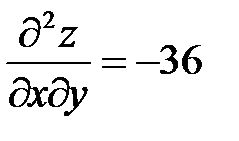 ;
; 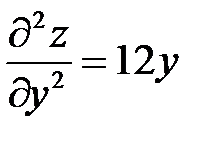 и составляем определитель
и составляем определитель 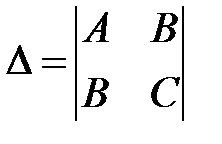 для каждой стационарной точки а)
для каждой стационарной точки а) 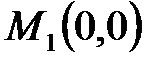 :
: 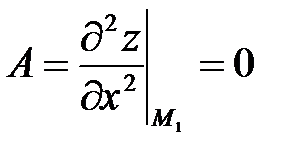 ;
; 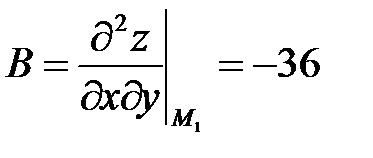 ;
; 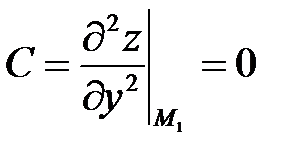
Получим число 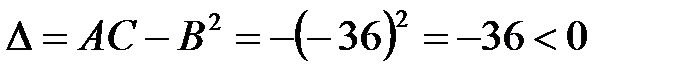 . Следовательно, в точке
. Следовательно, в точке 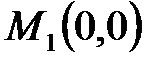 нет экстремума (ни максимума, ни минимума);
нет экстремума (ни максимума, ни минимума);
б) 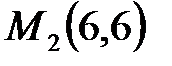 :
: 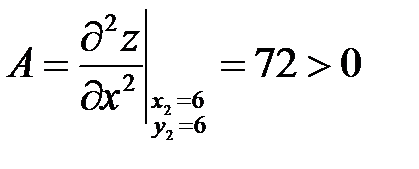 ;
; 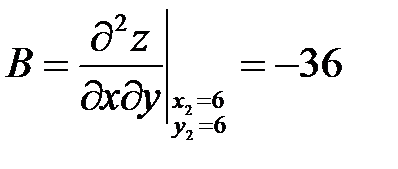 ;
; 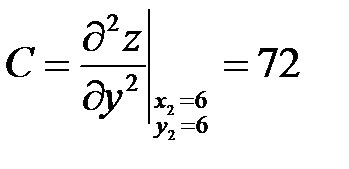 .
. 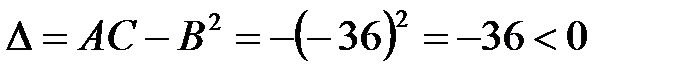 >0
>0
Следовательно, экстремум есть в точке 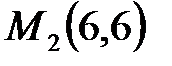 , причем минимум, так как A>0. Минимум этот равен значению функции при x=6, y=6:
, причем минимум, так как A>0. Минимум этот равен значению функции при x=6, y=6: 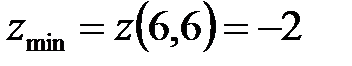 .
.
Приведем достаточные условия экстремума для функции трех независимых переменных, которые выражаются с помощью определителя третьего порядка.
Достаточные условия экстремума для функции
трех независимых переменных .
Эти условия выражаются с помощью определителя уже третьего порядка. Пусть дважды дифференцируемая функция 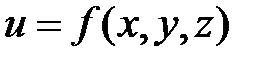 трех переменных имеет стационарную точку
трех переменных имеет стационарную точку 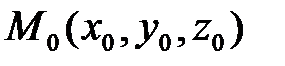 , найденную из системы уравнений:
, найденную из системы уравнений:
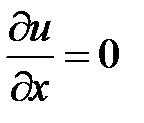 ;
; 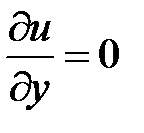 ;
; 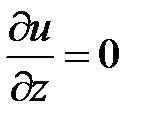 ; (необходимое условие экстремума)
; (необходимое условие экстремума)
Составляем определитель третьего порядка

и вычисляем его для каждой стационарной точки. Имеем следующее правило: Для того, чтобы функция 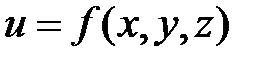 имела экстремум в точке
имела экстремум в точке 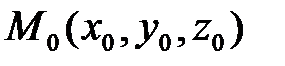 , достаточно, чтобы четный минор был положителен, а знаки нечетных миноров совпадали со знаком
, достаточно, чтобы четный минор был положителен, а знаки нечетных миноров совпадали со знаком 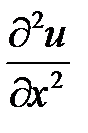 , то есть минор второго порядка
, то есть минор второго порядка 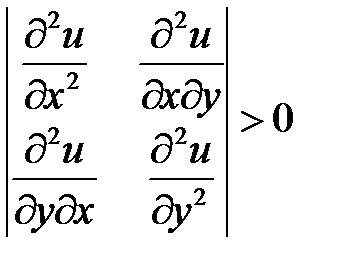 в точке
в точке 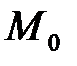 , причем: Если
, причем: Если 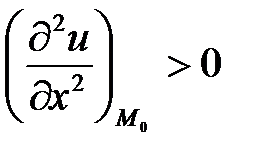 и
и 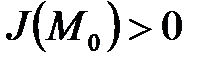 то имеем минимум функции в точке
то имеем минимум функции в точке 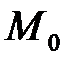 , если
, если 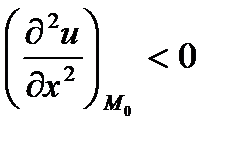 и
и 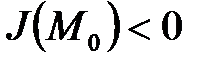 то имеем максимум функции в точке
то имеем максимум функции в точке 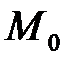 . Замечание: достаточно определить знак главного минора второго порядка.
. Замечание: достаточно определить знак главного минора второго порядка.
Пример2. Найти экстремум функции 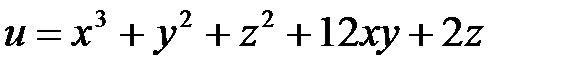 .
.
Решение. а) необходимое условие экстремума. Находим 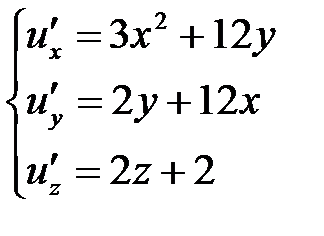 и решаем систему уравнений
и решаем систему уравнений 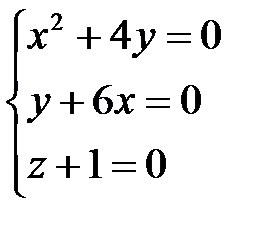 . Получим две стационарные точки M1(0,0,1) и M2(24,-144,-1).
. Получим две стационарные точки M1(0,0,1) и M2(24,-144,-1).
б) достаточные условия экстремума
Находим 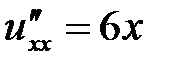 ,
, 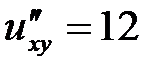 ,
, 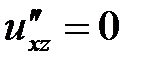 ,
, 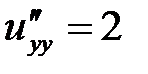 ,
, 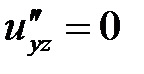 ,
, 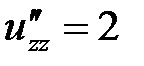 и составляем определитель
и составляем определитель
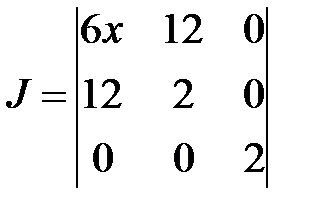 .
.
Исследуем на экстремум точку M1(0,0,1): четный минор 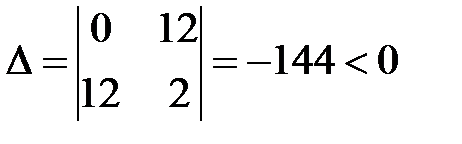 . Значит, в точке M1 экстремума нет.
. Значит, в точке M1 экстремума нет.
Исследуем точку M2(24,-144,-1) на экстремум. Ее четный минор 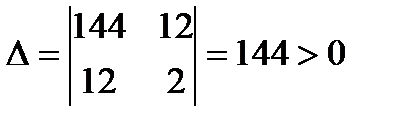 , а знаки нечетных миноров
, а знаки нечетных миноров
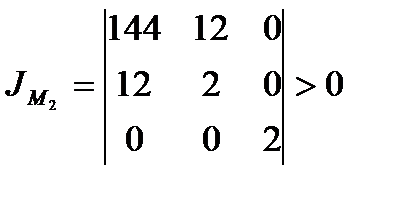 и
и 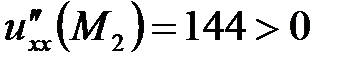 ,т.е.совпадают.
,т.е.совпадают.
Следовательно, в точке М2 есть экстремум, причем минимум 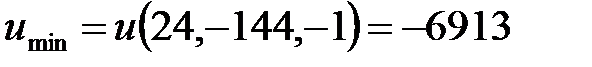 .
.
Дата: 2016-10-02, просмотров: 388.