Для того чтобы определить поверхностный интеграл второго рода, нужно ввести понятие стороны поверхности, аналогичное понятию ориентации кривой.
Пусть Σ – гладкая поверхность. Возьмем на Σ некоторую внутреннюю точку М0, проведем через нее нормаль к поверхности Σ и выберем на этой нормали одно из двух возможных направлений. Это можно сделать, зафиксировав определенный единичный вектор  , нормальный к поверхности Σ в точке М0. Проведем теперь на поверхности Σ через точку М0 какой-либо замкнутый контур С, не имеющий общих точек с границей поверхности, и будем двигать единичный вектор
, нормальный к поверхности Σ в точке М0. Проведем теперь на поверхности Σ через точку М0 какой-либо замкнутый контур С, не имеющий общих точек с границей поверхности, и будем двигать единичный вектор  из точки M0 вдоль С так, чтобы этот вектор все время оставался нормальным к Σ и чтобы его направление менялось при этом движении непрерывно. Поскольку вектор
из точки M0 вдоль С так, чтобы этот вектор все время оставался нормальным к Σ и чтобы его направление менялось при этом движении непрерывно. Поскольку вектор  все время остается нормальным к Σ, то имеются две возможности: при возвращении в точку M0 вектор
все время остается нормальным к Σ, то имеются две возможности: при возвращении в точку M0 вектор  возвращается в первоначальное положение; в результате обхода по контуру С вектор
возвращается в первоначальное положение; в результате обхода по контуру С вектор  меняет свое направление на противоположное.
меняет свое направление на противоположное.
Гладкая поверхность Σ называется двусторонней, если обход по любому замкнутому контуру, лежащему на поверхности Σ и не имеющему общих точек с ее границей, не меняет направления нормали к поверхности. Если же на поверхности существует замкнутый контур, по которому направление нормали меняется на противоположное (при движении ее по контуру), то поверхность называется односторонней. Если поверхность Σ двусторонняя, то в каждой ее точке М можно выбрать единичный вектор нормали  (М) так, чтобы вектор
(М) так, чтобы вектор  (М) зависел от точки М непрерывно (
(М) зависел от точки М непрерывно (  (М) будет называться «непрерывным полем нормалей» на поверхности Σ). На односторонней поверхности нельзя построить ни одного непрерывного поля нормалей. Выбор на поверхности Σ определенного непрерывного поля нормалей будет называться выбором стороны этой поверхности.
(М) будет называться «непрерывным полем нормалей» на поверхности Σ). На односторонней поверхности нельзя построить ни одного непрерывного поля нормалей. Выбор на поверхности Σ определенного непрерывного поля нормалей будет называться выбором стороны этой поверхности.
Замечания:
1. Двустороннюю поверхность называют ориентируемой, а выбор определенной ее стороны – ориентациейповерхности. Односторонние поверхности называют не ориентируемыми.
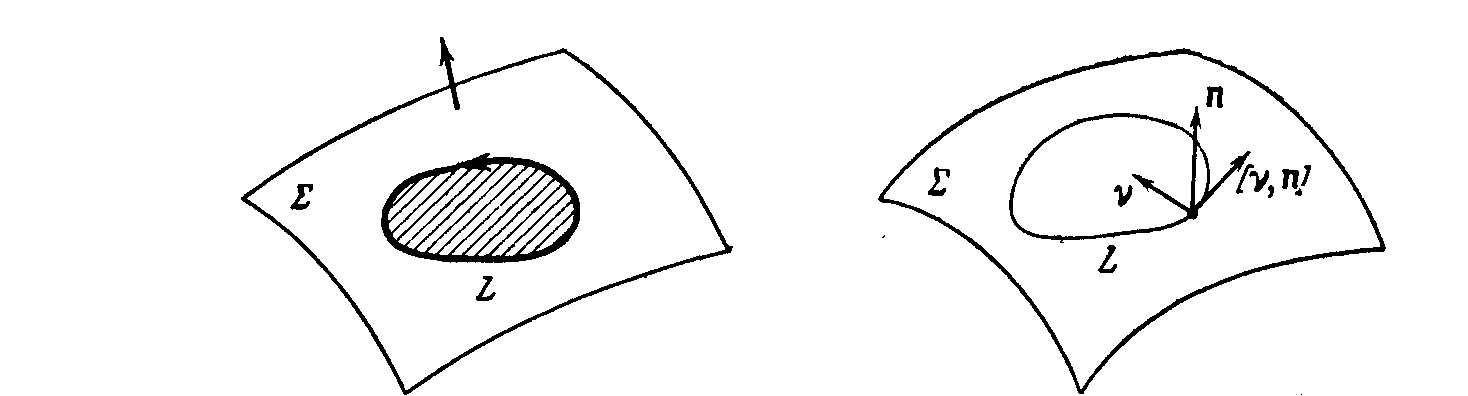
2. Пусть Σ – ориентированная поверхность, ограниченная одним или несколькими контурами. Определим ориентацию каждого контура L, входящего в состав границы поверхности Σ, (согласованную с ориентацией поверхности Σ) по следующему правилу. Направление обхода контура L считается положительным (согласованным с ориентацией Σ), если наблюдатель, расположен на поверхности так, что направление вектора нормали совпадает с направлением от ног к голове, обходит контур L, оставляя поверхность Σ все время слева от себя. Противоположное направление считается отрицательным.
3. Правило согласования ориентации поверхности Σ и ограничивающего ее контура L можно сформулировать таким образом: пусть  - единичный вектор нормали к поверхности Σ в некоторой точке М, принадлежащей L, и пусть
- единичный вектор нормали к поверхности Σ в некоторой точке М, принадлежащей L, и пусть 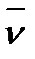 -вектор, нормальный к L и к
-вектор, нормальный к L и к  и направленный в ту сторону, с которой расположена поверхность Σ. Тогда положительное направление обхода контура L указывается вектором [
и направленный в ту сторону, с которой расположена поверхность Σ. Тогда положительное направление обхода контура L указывается вектором [ 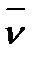 ,
, 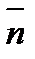 ]
]
|
Рис. 36.3 Рис. 36.4
Применение поверхностного интеграла второго рода
Пусть пространство заполнено движущейся жидкостью, скорость которой в точке (х, у, z) задается вектором 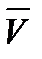 (х, у, z) cкомпонентами Р = Р(х, у, z),Q = Q(x, у, z), R = R(x, у, z).
(х, у, z) cкомпонентами Р = Р(х, у, z),Q = Q(x, у, z), R = R(x, у, z).
Вычислим количество жидкости П, протекающей за единицу времени через некоторую ориентированную поверхность Σ.
Рассмотрим бесконечно малый элемент dσ поверхности Σ. Количество жидкости, протекающее через dσ за единицу времени, равно dП = Vn, где Vn – проекция скорости 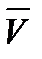 на направление нормали
на направление нормали  к dσ. Записав dП как скалярное произведение вектора V на единичный вектор нормали п к элементу dσ, имеем dП =[Р cos (
к dσ. Записав dП как скалярное произведение вектора V на единичный вектор нормали п к элементу dσ, имеем dП =[Р cos (  , х)+ Q cos (
, х)+ Q cos (  , у) + R cos (
, у) + R cos (  , z)] dσ.
, z)] dσ.
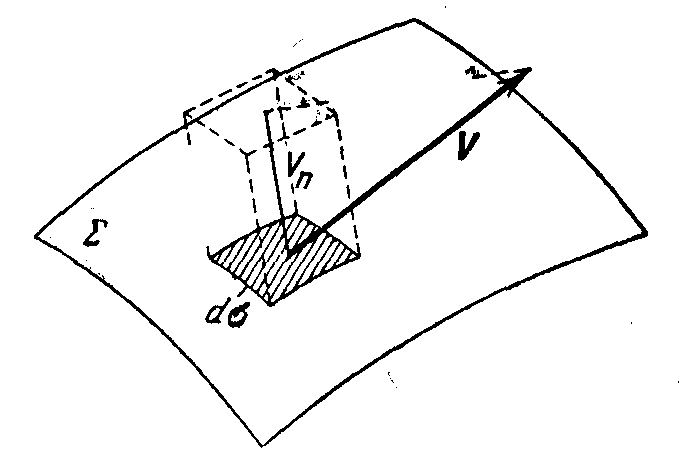
Рис. 36.5
Чтобы получить количество жидкости, протекающее через всю поверхность Σ, нужно просуммировать предыдущее выражение по всем элементам dσ, т. е. взять интеграл
П =  [Pcos(
[Pcos(  , x) + Qcos(
, x) + Qcos(  ,y) + Rcos(
,y) + Rcos(  , z)] dσ. (36.6)
, z)] dσ. (36.6)
Перейдем теперь к общему определению. Пусть Σ – гладкая двусторонняя поверхность. Фиксируем какую-либо определенную сторону поверхности (поле нормалей  (М)) и рассмотрим векторную функцию
(М)) и рассмотрим векторную функцию 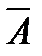 =(Р, Q, R), заданную на Σ. Обозначим Аn проекцию вектора
=(Р, Q, R), заданную на Σ. Обозначим Аn проекцию вектора 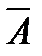 на направление нормали к Σ в данной точке
на направление нормали к Σ в данной точке
Аn = P cos (  , х) + Q cos (
, х) + Q cos (  , y)+ R cos (
, y)+ R cos (  , z),
, z),
где cos(  , x), cos(
, x), cos(  , у) и cos(
, у) и cos(  , z) – косинусы углов между направлением нормали к поверхности и направлениями координатных осей, т. е. координаты единичного вектора нормали n. Интеграл
, z) – косинусы углов между направлением нормали к поверхности и направлениями координатных осей, т. е. координаты единичного вектора нормали n. Интеграл
 [P cos(
[P cos(  , x) + Q cos(
, x) + Q cos(  , y)+ R cos(
, y)+ R cos(  , z)] dσ (36.7)
, z)] dσ (36.7)
называется поверхностным интегралом второго рода от вектор – функции 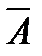 =(P, Q, R) по поверхности Σ (по выбранной стороне поверхности Σ) и будем обозначать
=(P, Q, R) по поверхности Σ (по выбранной стороне поверхности Σ) и будем обозначать
 P dydz + Q dzdx + R dxdy.
P dydz + Q dzdx + R dxdy.
При переходе к другой стороне поверхности координаты единичного вектора нормали, следовательно и сам интеграл, меняют свой знак на противоположный. Для односторонней поверхности понятие поверхностного интеграла второго рода не вводится. В соответствии с этим поверхностный интеграл второго рода от векторной функции 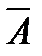 = (Р, Q, R) записывают в виде
= (Р, Q, R) записывают в виде
 (
( 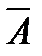 ,
, 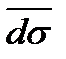 )=
)=  (
( 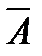 ,
,  )dσ. (36.8)
)dσ. (36.8)
Наряду с интегралами вида (4.5) в некоторых задачах приходится рассматривать интегралы вида
 [
[ 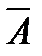 ,
,  ]dσ . (36.9)
]dσ . (36.9)
Значение такого интеграла представляет собой уже не скаляр, а вектор. Его вычисление сводится к покомпонентному интегрированию вектора [ 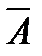 ,
,  ]. Так как здесь подынтегральное выражение зависит от нормали
]. Так как здесь подынтегральное выражение зависит от нормали  к поверхности Σ, то интеграл (36.9) будет поверхностным интегралом второго рода (но только «векторный», в отличие от «скалярного» интеграла).
к поверхности Σ, то интеграл (36.9) будет поверхностным интегралом второго рода (но только «векторный», в отличие от «скалярного» интеграла).
Сведение поверхностного интеграла второго
рода к двойному интегралу
Из определения поверхностного интеграла второго рода вытекает следующий результат Пусть гладкая (или кусочно-гладкая) поверхность Σ задана уравнением z = z(x, у) (причем берется верхняя сторона этой поверхности) и R (х, у, z) – некоторая ограниченная функция на поверхности Σ . Тогда
 R (х, у, z) dxdy =
R (х, у, z) dxdy = 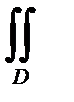 R (х, у, z (х, у)) dxdy, (36.10)
R (х, у, z (х, у)) dxdy, (36.10)
где D – проекция поверхности Σ на плоскость х0у; входящий в это равенство поверхностный интеграл существует, если существует стоящий справа двойной интеграл. Таким образом, для того, чтобы поверхностный интеграл  R(x,у,z) dσ, взятый по верхней стороне поверхности Σ (ее уравнение z = z(x, y)) преобразовать в двойной, следует вподынтегральную функцию вместо z подставитьфункцию z(x, у), а интегрирование по поверхности Σ заменить интегрированием по ее проекции D на плоскость х0у. Если же интеграл берется по нижней стороне поверхности Σ, то
R(x,у,z) dσ, взятый по верхней стороне поверхности Σ (ее уравнение z = z(x, y)) преобразовать в двойной, следует вподынтегральную функцию вместо z подставитьфункцию z(x, у), а интегрирование по поверхности Σ заменить интегрированием по ее проекции D на плоскость х0у. Если же интеграл берется по нижней стороне поверхности Σ, то
 R(x, у, z) dxdy = -
R(x, у, z) dxdy = - 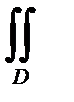 R(x, у, z(x, y))dxdy.
R(x, у, z(x, y))dxdy.
Так же получены формулы:
 P(x, у, z) dydz = ±
P(x, у, z) dydz = ± 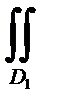 Р(х(у,z), у, z) dydz ;
Р(х(у,z), у, z) dydz ;
 Q(x, y, z) dzdx =±
Q(x, y, z) dzdx =± 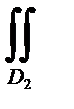 Q(x, y(z, x), z) dzdx,
Q(x, y(z, x), z) dzdx,
где в первом случае под поверхностью Σ понимается поверхность, заданная уравнением х = х(у, z), а во втором – поверхность, заданная уравнением у = у (z, х).
Знак плюс берется в том случае, когда нормаль к поверхности образует с осью х (соответственно с осью у) острый угол, а знак минус, когда этот угол тупой. D1 и D2 – проекции поверхности Σ на плоскости у0z и z0х соответственно. Формулой типа (36.10) можно воспользоваться для сведения поверхностного интеграла к двойному интегралу и в том случае, когда ориентированная поверхность Σ состоит из нескольких кусков, каждый из которых определяется уравнением вида z = z (х, у). В этом случае рассматриваемый интеграл следует представить как сумму интегралов, отвечающих этим кускам, и затем к каждому из этих слагаемых применить формулу (36.10).
Пример 3 . Вычислить поверхностный интеграл
J = 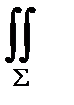 (x2 + y2)3dxdy , где Σ – верхняя часть круга x2 + y2 = 1.
(x2 + y2)3dxdy , где Σ – верхняя часть круга x2 + y2 = 1.
Решение.Поверхность, по которой берется интеграл совпадает со своей проекцией на плоскость XOY D (D: x2 + y2≤ 1) и имеет c ней положительную ориентацию. Применяя полярную систему координат ( x = r cos φ , y = r sin φ, 0≤ r ≤1, 0≤ φ≤ 2π ), имеем J = 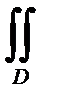 (x2 + y2)3dxdy =
(x2 + y2)3dxdy = 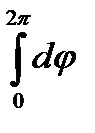
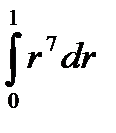 =π/4.
=π/4.
Формула Остроградского
Запишем формулу, связывающую тройной интеграл по пространственной области с поверхностным интегралом, взятым по внешней стороне поверхности, ограничивающей эту область. Эта формула называется формулой Остроградского.
Пусть, наконец, V – некоторая простая область с поверхностью Σ и пусть функции Р, Q, R вместе со своими производными непрерывны в этой области всюду, включая ее границу, тогда можно записать равенство
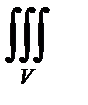 ((∂P/∂x) + (∂Q/∂y) + (∂R/∂z)) dxdydz =
((∂P/∂x) + (∂Q/∂y) + (∂R/∂z)) dxdydz =  P dydz +Qdzdx+
P dydz +Qdzdx+
+ R dxdy =  [P cos(
[P cos(  , x + Q cos(
, x + Q cos(  , y + R cos(
, y + R cos(  , z)]dσ. (36.11)
, z)]dσ. (36.11)
Замечание. При выводе формулы Остроградского мы считали, что функции Р, Q, R и их частные производные непрерывны (а следовательно, и ограничены) в замкнутой простой области. Можно доказать справедливость формулы Остроградского при следующих более общих условиях:
1. V – ограниченная область, граница которой состоит из конечного числа кусочно-гладких поверхностей.
2. Функции Р (х, y, z), Q (х, у, z) и R (х, у, z) непрерывны, а следовательно, и ограничены в замкнутой области V.
3. Производные ∂P/∂x, ∂Q/∂y, ∂R/∂z существуют и непрерывны внутри области V (безграницы) и интеграл
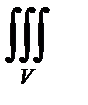 [(∂P/∂x) + (∂Q/∂y) + (∂R/∂z)] dxdydz существует.
[(∂P/∂x) + (∂Q/∂y) + (∂R/∂z)] dxdydz существует.
Пример 4.Вычислить интеграл J =  x3 dydz +
x3 dydz +
+ y3 dzdx + z3 dxdy, взятый по сфере х2 + у2 +z2 = a2.
Решение. Воспользовавшись формулой Остроградскогоимеем
J=3 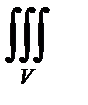 (x2 + y2 + z2) dxdydz = 3
(x2 + y2 + z2) dxdydz = 3 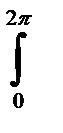 dφ
dφ 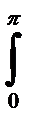 dθ
dθ 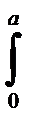 r4 sinθ dr =
r4 sinθ dr =
= 0,8π a5, где r, φ , θ – сферические координаты.
Формула Стокса
Выведем формулу Стокса, которая связывает поверхностные и криволинейные интегралы. Формула Стокса обобщает формулу Грина и переходит в нее, если поверхность сводится к плоской области X0Y.
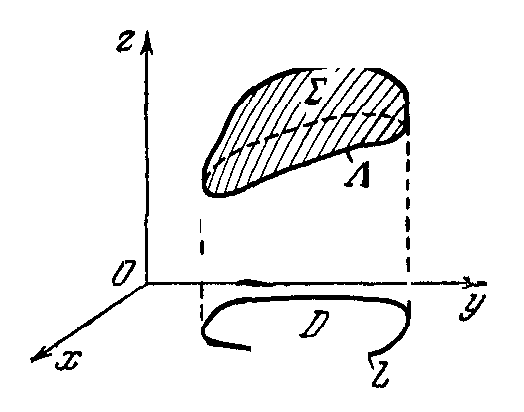
Рис. 36.6
Пусть дана гладкая ориентированная поверхность Σ, ограниченная ориентированным контуром Λ, (ориентации Σ и Λ согласованы), и пусть в некоторой трехмерной области, содержащей внутри себя поверхность Σ, определена векторная функция (P, Q, R), такая, что Р, Q и R непрерывны в этой области вместе со своими частными производными первого порядка.
Формула Стокса имеет вид:
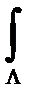 P dx + Q dy + R dz =
P dx + Q dy + R dz =  [
[ 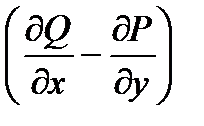 cos(
cos(  , z) +
, z) +
+ 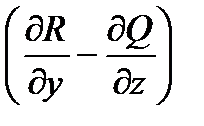 cos(
cos(  , x) +
, x) + 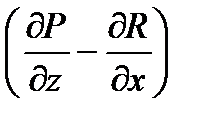 cos(
cos(  , y)] dσ =
, y)] dσ =
= 
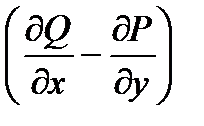 dxdy+
dxdy+ 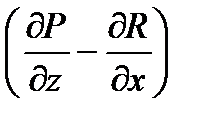 dydz+
dydz+ 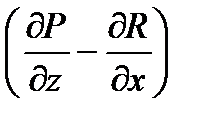 dzdx. (36.12)
dzdx. (36.12)
Если поверхность Σ сводится к плоской области, лежащей в плоскости х0у, то интегралы по dzdx и dydz обращаются в нуль и формула Стокса переходит в формулу Грина.
Замечание. Формула Стокса остается в силе в случае, когда граница контура Λ (поверхности Σ) состоит из нескольких отдельных контуров. Интеграл по контуру Λ понимаем как сумму интегралов, взятых по этим контурам, причем ориентация каждого из этих контуров должна быть согласована с выбором стороны поверхности Σ.
Определение. Трехмерная область V называется односвязной, если на любой замкнутый контур, лежащий в V, можно натянуть поверхность, также целиком лежащую в V(т.е. если внутри V найдется поверхность, имеющая этот контур своей границей).
Если функции Р (х, у, z), Q(x, у, z), R(x, у, z) непрерывны,вместе со своими частными производными первого порядка в некоторой замкнутой ограниченной поверхностно односвязной области V, то можно доказать следующие свойства:
1. Интеграл 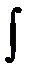 Р dх + Q dy +R dz, взятый по любому замкнутомуконтуру, лежащему внутри V, равен нулю.
Р dх + Q dy +R dz, взятый по любому замкнутомуконтуру, лежащему внутри V, равен нулю.
2. 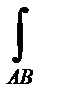 Р dx + Q dy + R dz не зависит от выбора пути, соединяющего точки А и В.
Р dx + Q dy + R dz не зависит от выбора пути, соединяющего точки А и В.
3. P dx+ Q dy+ R dz – полный дифференциал некоторой однозначной функции, определенной в V.
4. Выполняются равенства
(∂Q/∂x) = (∂Р/∂y), (∂R/∂у) = (∂Q/∂z),
(∂P/∂z) = (∂R/∂x). (36.13)
Рассмотрим некоторый замкнутый контур Λ, лежащий в V, так как область V по условию односвязна, то на Λ можно натянуть поверхность Σ, целиком лежащую внутри V. Применив к криволинейному интегралу, взятому поΛ, формулу Стокса получаем равенство
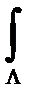 P dx + Q dy + R dz = 0.
P dx + Q dy + R dz = 0.
Если выражение Р dx + Q dy + R dz представляет собой полный дифференциал некоторой функции U (x, у, z), то можно написать выражение этой функции
U(x, у, z)= 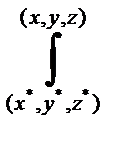 ∫ P dx + Q dy + R dz, (36.14)
∫ P dx + Q dy + R dz, (36.14)
где интеграл взят по произвольному пути M ΄M ( M ΄(x΄, y΄, x΄), M(х, у, z)), целиком лежащему в области V.
Если функцииР, Q иR удовлетворяют условиям (36.13), но область, в которой они определены, не односвязна, то свойства интеграла 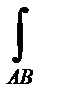 P dx + Q dy + R dz аналогичны свойствам криволинейного интеграла
P dx + Q dy + R dz аналогичны свойствам криволинейного интеграла 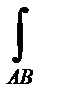 Р dx+ Q dy в плоской многосвязной области.
Р dx+ Q dy в плоской многосвязной области.
В частности, равенство (36.14) при выполнении (36.13) и в случае многосвязной области представляет собой функцию, полный дифференциал которой равен Р dx + Q dy + R dz, но в многосвязной области эта функция многозначна.
Теория поля
Понятие поля лежит в основе многих представлений современной физики. Изложим элементы того математического аппарата, которым приходится пользоваться при изучении физических полей. В физических задачах чаще всего встречаются величины двух типов: скаляры и векторы. В соответствии с этим мы будем рассматривать два типа полей – скалярные и векторные.
Скалярные поля
Пусть Ω - некоторая область в пространстве. В этой области задано скалярное поле, если каждой точке М этой области поставлено в соответствие некоторое число U (М).
Примерами скалярных полей служат: поле температур внутри некоторого нагретого тела (в каждой точке М этого тела задана соответствующая температура U (М)); поле освещенности, создаваемое каким-либо источником света; поле плотности массы и т.д.
Пусть U(М) – некоторое скалярное поле, то, введя в области, где задано поле, декартовы координаты, можно представить это поле в виде непрерывной функции U(x, у, z).
Для получения наглядной картины удобно пользоваться называемыми поверхностями уровня. Поверхностью уровня скалярного поля U (M) называется геометрическое место точек, в которых полеимеет вид U(x, у, z) = С. Этот способ изображения поля также удобен тогда, когда поле, задано не в пространственной, а в плоской области. Такое поле описывается функцией двух переменных U(x, у). Кривые вида
U(x, у) = С определяют линию уровня плоского скалярного поля U (М).
Частные случаи: Плоскопараллельное поле. Если скалярное поле U (М) в декартовой системе координат можно описать функцией, зависящей от двух координат (U(x, у)), то поле называется плоскопараллельным (двумерным). Поле U (M) называется плоскопараллельным, если в пространстве существует направление, при сдвигах вдоль которого поле U (M) переходит само в себя. Поверхности уровня такого поля – это семейство (U(x, y) = C) цилиндрических поверхностей.
Осесимметрическое поле. Если для поля U (M) можно подобрать такую цилиндрическую систему координат, в которой оно изображается функцией, зависящей только от переменных r = (х2+ у2)1/2 и z (но не от угла φ), то это поле называется осесимметрическим. Поверхности уровня такого поля представляют собой поверхности вращения.
Сферическое поле. Если значения U (М) зависят лишь от расстояния точки М от некоторойфиксированной точки М0,то такое поле называется сферическим. Поверхности уровня сферичеcкого поля будут являе тся семейством концентрических сфер .
Пример 1. Найти область определения функции
z =1 /(x2 + y2) иопределить линии уровня скалярного поля z.
Решение. Поле z определено во всем пространстве за исключением точек, для которых x2+y2=0, т.е. x = 0, y = 0.
Линии уровня определяются уравнением 1/(x2+y2) = C,
C (x2 + y2) = 1 – уравнения семейства окружностей.
Производная по направлению
Пусть U (М) – скалярное поле. Рассмотрим две близкие точки М М*, причем направление отрезка ММ* совпадает с направлением фиксированного единичного вектора 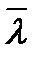 . Если при этом отношение (U(M*) – U(M))/h (где h – длина отрезка ММ*) стремится к некоторому пределу, то этот предел называется производной скалярного поля U (М) в точке М по направлению
. Если при этом отношение (U(M*) – U(M))/h (где h – длина отрезка ММ*) стремится к некоторому пределу, то этот предел называется производной скалярного поля U (М) в точке М по направлению 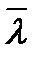 и обозначается ∂U(M)/∂λ . Эта производная характеризует скорость изменениявеличины U(M) в направлении
и обозначается ∂U(M)/∂λ . Эта производная характеризует скорость изменениявеличины U(M) в направлении 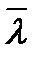 . Для ее вычисления выберем некоторую систему координат и представим U(М) в виде U(x, у, z).
. Для ее вычисления выберем некоторую систему координат и представим U(М) в виде U(x, у, z).
Пусть направление 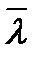 образует с осями координат углы α,β,γ. Тогда ММ* = h (icos α+ jcos β + kcosγ) и U (М*)= U (х+ hcosa, y+hcosβ, z+hcosγ), а производная ∂U/∂λ- совпадает с производной по h от сложной функции U(M*) при h = 0. Дифференцируя, получаем
образует с осями координат углы α,β,γ. Тогда ММ* = h (icos α+ jcos β + kcosγ) и U (М*)= U (х+ hcosa, y+hcosβ, z+hcosγ), а производная ∂U/∂λ- совпадает с производной по h от сложной функции U(M*) при h = 0. Дифференцируя, получаем
∂U(М)/∂ 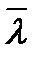 =(∂U(М*)/∂
=(∂U(М*)/∂ 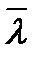 )│h=0=(∂U/∂x)cosα + (∂U/∂y)cosβ +(∂U/∂z)cosγ = (grad U,
)│h=0=(∂U/∂x)cosα + (∂U/∂y)cosβ +(∂U/∂z)cosγ = (grad U, 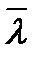 ). где
). где 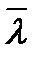 =(cosα, cosβ, cosγ)/∂z, вектор gradU=(∂U/∂x, ∂U/∂y, ∂U/∂z) называется градиентом скалярного поля U. Из того, что (∂U/∂
=(cosα, cosβ, cosγ)/∂z, вектор gradU=(∂U/∂x, ∂U/∂y, ∂U/∂z) называется градиентом скалярного поля U. Из того, что (∂U/∂ 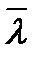 )=│grad U│ cosφ (где φ – угол между grad U и единичным вектором
)=│grad U│ cosφ (где φ – угол между grad U и единичным вектором 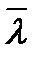 ), можно заключить: в каждой точке, где значение grad U не равно 0 существует единственное направление, по которому ∂U/∂
), можно заключить: в каждой точке, где значение grad U не равно 0 существует единственное направление, по которому ∂U/∂ 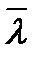 имеет наибольшее значение, т.е. единственное направление наибыстрейшего возрастания функции U. Это направление совпадает с направлением вектора grad U.
имеет наибольшее значение, т.е. единственное направление наибыстрейшего возрастания функции U. Это направление совпадает с направлением вектора grad U.
Назовем линией градиента скалярного поля U всякую кривую, касательная к которой в каждой ее точке направлена по grad U в этой же точке. Линии градиента поля – это те линии, вдоль которых поле U меняется быстрее всего. В каждой точке линия градиента ортогональна той поверхности уровня, на которой эта точка лежит.
Векторные поля
Пусть в некоторой области Ω определено векторное поле, тогда каждойточке М этой области будет поставлен в соответствие определенный вектор  (М).
(М).
Если  (М) – некоторое векторное поле в пространстве, то, взяв в этом пространстве какую-либо декартову систему координат, мы можем представить
(М) – некоторое векторное поле в пространстве, то, взяв в этом пространстве какую-либо декартову систему координат, мы можем представить  (М) как совокупность трех скалярных функций – компонент этого вектора. Эти компоненты мы будем обозначать Р(х, у, z), Q(x, у, z) и R(x, у, z). Далее мы будем рассматривать векторные поля, компоненты которых непрерывны и имеют непрерывные частные производные первого порядка.
(М) как совокупность трех скалярных функций – компонент этого вектора. Эти компоненты мы будем обозначать Р(х, у, z), Q(x, у, z) и R(x, у, z). Далее мы будем рассматривать векторные поля, компоненты которых непрерывны и имеют непрерывные частные производные первого порядка.
Пусть в области Ω задано векторное поле  (M). Кривая L лежащая в Ω, называется векторной линией, если в каждой точке этой кривой направление касательной к ней совпадает с направлением вектора
(M). Кривая L лежащая в Ω, называется векторной линией, если в каждой точке этой кривой направление касательной к ней совпадает с направлением вектора  в этой же точке.
в этой же точке.
Рассмотрим снова некоторое скалярное поле U(М). Построив в каждой точке М вектор grad U, мы получим векторное поле – поле градиента скалярной величины U. Введем следующее: Векторное поле  (М) называется потенциальным, если егоможно представить как градиент некоторого скалярного поля U (М):
(М) называется потенциальным, если егоможно представить как градиент некоторого скалярного поля U (М):  = grad U. Само скалярное поле U называется при этом потенциалом векторного поля
= grad U. Само скалярное поле U называется при этом потенциалом векторного поля  .
.
Если векторное поле  имеет потенциал, то этот потенциал определяется полем
имеет потенциал, то этот потенциал определяется полем  однозначно, с точностью до произвольного постоянного слагаемого. Векторные линии потенциального поля
однозначно, с точностью до произвольного постоянного слагаемого. Векторные линии потенциального поля  представляют собой, линиями градиента его потенциала U, т. е. линии наибыстрейшего изменения этого потенциала. Условия, при которых данное векторное поле А потенциально:
представляют собой, линиями градиента его потенциала U, т. е. линии наибыстрейшего изменения этого потенциала. Условия, при которых данное векторное поле А потенциально:
∂P/∂y = ∂Q/∂x, ∂Q/∂z = ∂R/∂y, ∂P/∂z = ∂R/∂x, (37.1)
но P dx + Q dy + R dz = dU, то P = ∂U/∂x, Q = ∂U/∂y, R = ∂U/∂z (эти формулы можно легко получить из свойств, полученных при выводе формулы Стокса).
Для того, чтобы векторное поле  = (Р, Q, R), имеющее непрерывные и непрерывно дифференцируемые компоненты, было потенциальным, необходимо и достаточно, чтобы выполнялись равенства (37.1).
= (Р, Q, R), имеющее непрерывные и непрерывно дифференцируемые компоненты, было потенциальным, необходимо и достаточно, чтобы выполнялись равенства (37.1).
Если  - потенциальное векторное поле, то нахождение его потенциала сводится к нахождению функции по ее полному дифференциалу.
- потенциальное векторное поле, то нахождение его потенциала сводится к нахождению функции по ее полному дифференциалу.
Пример 2 . Найти векторные линии в векторном поле
 =4z j + 8yk.
=4z j + 8yk.
Решение.Так как 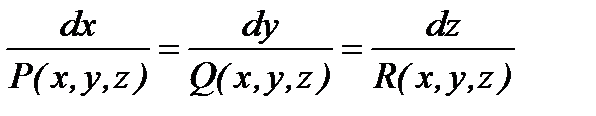 , то имеем
, то имеем 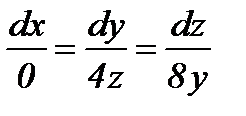 ,
, 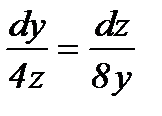 , dx = 0. Интегрируя систему, получим
, dx = 0. Интегрируя систему, получим
X = h (h=const), 2y2 = z2 + c – семейство гипербол, лежащих
в плоскостях параллельных плоскости YOZ.
Поток векторного поля. Дивергенция
Количество жидкости, протекающей за единицу времени через данную (ориентированную) поверхность Σ, равно интегралу  Аn dσ,где An – нормальная составляющая вектора скорости
Аn dσ,где An – нормальная составляющая вектора скорости  = ( Р, Q, R). Величина П называется потоком жидкости через поверхность Σ. Пусть
= ( Р, Q, R). Величина П называется потоком жидкости через поверхность Σ. Пусть  произвольное векторное поле и Σ ориентированная поверхность. Поток:
произвольное векторное поле и Σ ориентированная поверхность. Поток:
П =  Аn dσ (37.2)
Аn dσ (37.2)
мы назовем потоком векторного поля  через поверхность.
через поверхность.
Пусть  - некоторое векторное поле. Поставим в соответствие каждой пространственной области Ω, ограниченной гладкой или кусочно-гладкой поверхностью Σ, величину
- некоторое векторное поле. Поставим в соответствие каждой пространственной области Ω, ограниченной гладкой или кусочно-гладкой поверхностью Σ, величину
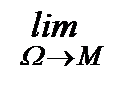 (1/V(Ω))
(1/V(Ω))  An dσ (37.3)
An dσ (37.3)
и назовем ее потоком вектора А через внешнюю сторону поверхности Σ. Мы получим аддитивную функцию области Ф(Ω). Производная функции Ф (Ω) по объему, т.е. предел (37.3) называется дивергенцией векторного поля  и обозначается div
и обозначается div  . Если
. Если  = (P, Q, R) – векторное поле, определенное в области Ω и такое, что функции Р, Q, R непрерывны в Ω вместе со всеми своими первыми производными, то div
= (P, Q, R) – векторное поле, определенное в области Ω и такое, что функции Р, Q, R непрерывны в Ω вместе со всеми своими первыми производными, то div  существует во всех точках этой области (в любой декартовой системе координат) и выражается формулой
существует во всех точках этой области (в любой декартовой системе координат) и выражается формулой
div  = ∂P/∂x + ∂Q/∂y + ∂R/∂z. (37.4)
= ∂P/∂x + ∂Q/∂y + ∂R/∂z. (37.4)
Пользуясь этим понятием, формула Остроградского будет:
 Аn dσ =
Аn dσ = 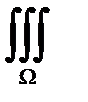 div
div  dv, (37.5)
dv, (37.5)
т.е. поток вектора  через внешнюю сторону замкнутой поверхности Σ равен интегралу от дивергенции поля
через внешнюю сторону замкнутой поверхности Σ равен интегралу от дивергенции поля  , взятому по области, ограниченной поверхностью Σ.
, взятому по области, ограниченной поверхностью Σ.
Соленоидальное поле
Векторное поле, дивергенция которого тождественно равна нулю, называется соленоидальным или трубчатым. Для соленоидальных полей выполнен закон сохранения интенсивности векторной трубки. Пусть 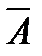 соленоидальное поле. Рассмотрим некоторую векторную трубку (поверхность, состоящая из векторных линий) и возьмем ее отрезок, заключенный между двумя ее сечениями Σ1 и Σ2 (рис. 37.1).
соленоидальное поле. Рассмотрим некоторую векторную трубку (поверхность, состоящая из векторных линий) и возьмем ее отрезок, заключенный между двумя ее сечениями Σ1 и Σ2 (рис. 37.1).

Рис. 37.1
Эти сечения вместе с боковой поверхностью Σ трубки образуют замкнутую поверхность Σ3. Так как поле соленоидально, т.е. div 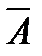 ≡ 0, в силу формулы Остроградского
≡ 0, в силу формулы Остроградского
 An dσ=
An dσ= 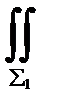 An dσ+
An dσ+ 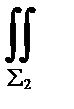 An dσ+
An dσ+ 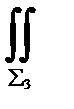 An dσ = 0 , (37.6)
An dσ = 0 , (37.6)
причем в каждом из слагаемых имеется в виду внешняя сторона поверхности. Интеграл по поверхности Σ3 равен нулю, так как по определению векторной трубки на поверхности Σ3 направление векторного поля  перпендикулярно направлению нормали кэтой поверхности. На Σ3 величина An ≡ 0 . Если теперь на сечении Σ1 направление нормали изменим на противоположное, то равенство (37.6) можно записать в виде:
перпендикулярно направлению нормали кэтой поверхности. На Σ3 величина An ≡ 0 . Если теперь на сечении Σ1 направление нормали изменим на противоположное, то равенство (37.6) можно записать в виде:
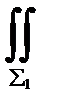 An dσ =
An dσ = 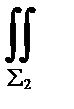 An dσ , (37.7)
An dσ , (37.7)
т.е. поток вектора 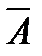 через любое сечение векторной трубки имеет одно и то же значение.
через любое сечение векторной трубки имеет одно и то же значение.
Уравнение неразрывности
Выведем уравнение движения жидкости, так называемого уравнения неразрывности.
Пусть 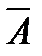 - поле скоростей движущейся жидкости. Мы будем предполагать, что в рассматриваемой области жидкость не исчезает и не возникает. Мы будем предполагать эту жидкость сжимаемой, т.е. считать плотность ρ некоторой функцией координат х, у, z и времени t.
- поле скоростей движущейся жидкости. Мы будем предполагать, что в рассматриваемой области жидкость не исчезает и не возникает. Мы будем предполагать эту жидкость сжимаемой, т.е. считать плотность ρ некоторой функцией координат х, у, z и времени t.
Тогда ∂ρ/∂t = - div(ρ 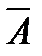 ) – уравнение, связывающее между собой скорость и плотность движущейся жидкости при отсутствии источников и стоков. Оно называется уравнением неразрывности. Если ввести вектор J = ρ
) – уравнение, связывающее между собой скорость и плотность движущейся жидкости при отсутствии источников и стоков. Оно называется уравнением неразрывности. Если ввести вектор J = ρ 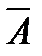 плотность потока жидкости, то уравнение неразрывности будет
плотность потока жидкости, то уравнение неразрывности будет
∂ρ/∂t + divJ = 0. (37.8)
Дата: 2016-10-02, просмотров: 323.