Рассмотрим плоское векторное поле  , т.е. поле, компоненты которого в некоторой декартовой системе координат имеют вид
, т.е. поле, компоненты которого в некоторой декартовой системе координат имеют вид
Р = Р(х, у), Q = Q(x, у), R = 0 . (37.9)
Дивергенция такого поля равна ∂P/∂x + ∂Q/∂y. Пусть Ω - цилиндр единичной высоты, с основанием G, лежащим в плоскости х0у, и боковой поверхностью Σ (рис. 37.2).
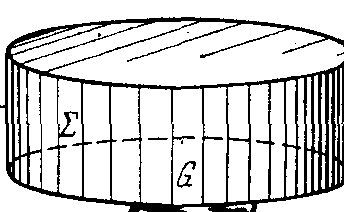 Рис. 37.2
Рис. 37.2
|
Запишем для области Ω формулу Остроградского, предварительно заметив, что тройной интеграл от div  численно равен двойному интегралу от этого выражения по плоской области G, поток вектора (37.2) через поверхность Σ равен криволинейному интегралу
численно равен двойному интегралу от этого выражения по плоской области G, поток вектора (37.2) через поверхность Σ равен криволинейному интегралу
П = 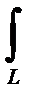 [P cos(
[P cos( 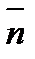 , x)+Q cos(
, x)+Q cos( 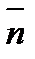 , y)] dl=
, y)] dl=
= 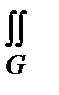 [∂P/∂x + ∂Q/∂y] dxdy (37.10)
[∂P/∂x + ∂Q/∂y] dxdy (37.10)
где 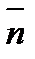 - нормаль к контуру L, а поток через верхнее и нижнее основания цилиндра Ω равен нулю (последнее вытекает из того, что вектор (37.10) перпендикулярен оси z). Отбросим теперь окончательно третью координату z, будем рассматривать (37.10) как векторное поле, заданное в плоскости хоу. Назовем криволинейный интеграл
- нормаль к контуру L, а поток через верхнее и нижнее основания цилиндра Ω равен нулю (последнее вытекает из того, что вектор (37.10) перпендикулярен оси z). Отбросим теперь окончательно третью координату z, будем рассматривать (37.10) как векторное поле, заданное в плоскости хоу. Назовем криволинейный интеграл
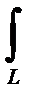 [P cos(
[P cos( 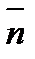 , x) + Q cos(
, x) + Q cos( 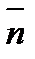 , y)] dl (37.11)
, y)] dl (37.11)
потоком этого векторного поля через контур L. Формула (37.10), так называемая формула Остроградского для плоскости, означает, что двойной интеграл от дивергенции плоского поля  по некоторой области G равен потоку вектора
по некоторой области G равен потоку вектора  через границу этой области. Формула (37.10) – просто эквивалент формулы Грина. Таким образом, как формула Стокса, так и формула Остроградского в плоском случае превращаются в формулу Грина.
через границу этой области. Формула (37.10) – просто эквивалент формулы Грина. Таким образом, как формула Стокса, так и формула Остроградского в плоском случае превращаются в формулу Грина.
Циркуляция векторного поля
Пусть  = (Р,Q, R) – некоторое векторное поле и L – гладкая или кусочно-гладкая кривая. Криволинейный интеграл
= (Р,Q, R) – некоторое векторное поле и L – гладкая или кусочно-гладкая кривая. Криволинейный интеграл
Ц = 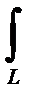 P dx + Q dy + R dz =
P dx + Q dy + R dz =  Aτ dl,
Aτ dl,
где aτ – тангенциальная составляющая поля А на контуре L, которую назовем циркуляцией векторного поля А вдоль кривой L. Если  =(Р, Q, R) – силовое поле, то его циркуляция вдоль кривой L представляет работу этого силового поля вдоль пути L. Для полей иной природы циркуляция имеет другой физический символ.
=(Р, Q, R) – силовое поле, то его циркуляция вдоль кривой L представляет работу этого силового поля вдоль пути L. Для полей иной природы циркуляция имеет другой физический символ.
Пример 3. Найти циркуляцию векторного поля
 = xi – zj + yk L пересечение поверхности у2 = 4 – x – z с координатными плоскостями(рис. 37.3).
= xi – zj + yk L пересечение поверхности у2 = 4 – x – z с координатными плоскостями(рис. 37.3).
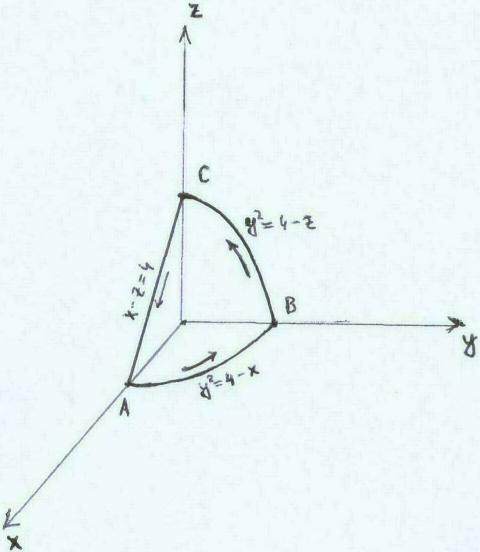
Рис. 37.3
Решение. Циркуляция вдоль кривой L вычисляется по формуле
Ц= 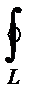

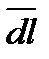 =
= 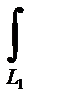

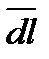 +
+ 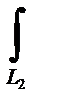

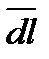 +
+ 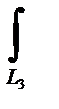

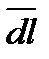 = 32/3,
= 32/3,
где
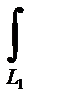

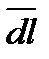 = -
= - 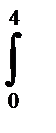 xdx= -x2/2
xdx= -x2/2 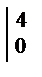 = -8. Так как L1=
= -8. Так как L1= 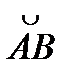 : z = 0, dz = 0, y2=4 – x, x є [0,4],
: z = 0, dz = 0, y2=4 – x, x є [0,4], 
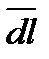 = xdx;
= xdx;
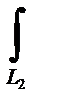

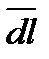 = -
= -  (y2+4)dy = y3/3+4y
(y2+4)dy = y3/3+4y  = 32/3.
= 32/3.
Так как L2=  : x = 0,
: x = 0,
dx = 0, z = 4 – y2, dz =- 2ydy, yє [0,2], 
 = -zdy+ ydz;
= -zdy+ ydz;
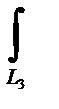

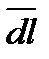 =
= 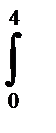 xdx=x2/2
xdx=x2/2 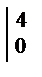 = 8. Так как L3 =
= 8. Так как L3 = 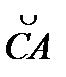 : y = 0,
: y = 0,
dy = 0, z+ x = 4, xє [0,4], 
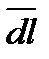 =xdx.
=xdx.
Ротор векторного поля
Если L - замкнутый контур, то формула имеет тот же вид
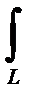 P dx + Q dy + R dz =
P dx + Q dy + R dz = 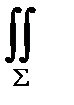 [(∂Q/∂x - ∂P/∂y) dxdy + (∂R/∂y -
[(∂Q/∂x - ∂P/∂y) dxdy + (∂R/∂y -
- ∂Q/∂z) dydz+ (∂P/∂z - ∂R/∂x)] dzdx, (37.12)
где поверхностный интеграл взят по некоторой поверхности Σ, натянутой на контур L. Правая часть равенства (37.12) представляет собой поток через поверхность Σ вектора. Назовем этот вектор ротором (или вихрем) векторного поля  и обозначим rot
и обозначим rot  . Таким образом,
. Таким образом,
rot  = (∂R/∂y - ∂Q/∂z) i + (∂P/∂z - ∂R/∂x) j + (∂Q/∂x - ∂P/∂y) k.
= (∂R/∂y - ∂Q/∂z) i + (∂P/∂z - ∂R/∂x) j + (∂Q/∂x - ∂P/∂y) k.
Пользуясь понятием ротора, можно записать формулу Стокса в следующем компактном виде
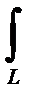 Aτ dl =
Aτ dl = 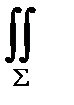 (rot
(rot  )n dσ. (37.13)
)n dσ. (37.13)
циркуляция векторного поля  вдоль некоторого замкнутого контура L равна потоку ротора этого векторного поля через поверхность, натянутую на этот контур.
вдоль некоторого замкнутого контура L равна потоку ротора этого векторного поля через поверхность, натянутую на этот контур.
В определении ротора участвует не только само векторное поле  , но и некоторая определенная система координат (x, у, z). Однако на самом деле вектор rot
, но и некоторая определенная система координат (x, у, z). Однако на самом деле вектор rot  не зависит от выбора координатной системы.
не зависит от выбора координатной системы.
Циркуляция вектора  вдоль контура не зависит от выбора координатной системы.
вдоль контура не зависит от выбора координатной системы.
Направление нормали 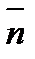 выбрано произвольно, поэтому проекция вектора rot
выбрано произвольно, поэтому проекция вектора rot  на любое направление, а следовательно и сам вектор rot
на любое направление, а следовательно и сам вектор rot  , не зависят от выбора системы координат.
, не зависят от выбора системы координат.
Ротор векторного поля  = (Р, Q, R) удобно записывать в виде символического определителя,
= (Р, Q, R) удобно записывать в виде символического определителя,
| i j k det= ∂/∂x ∂/∂y ∂/∂z PQ R |
гдеi, j, k – единичные векторы, направленные по осям координат,а под умножением символа ∂/∂x,∂ /∂y, ∂/∂z на некоторую функцию понимается выполнение соответствующей операции дифференцирования (например, (∂/∂x)R означает ∂R/∂x).
Действительно, разложив определитель по элементам первой строки, получим, что det = rot  .
.
Мы назвали потенциальным векторное поле, представимое в виде градиента некоторого скалярного поля, и показали, что векторное поле  = (Р, Q, R) потенциально в том и только том случае, если его компоненты удовлетворяют условиям ∂P/∂y = ∂Q/∂x, ∂Q/∂z = ∂R/∂y, ∂R/∂x = ∂P/∂z, но эти три условия означают не что иное, как равенство нулю всех трех компонент ротора поля
= (Р, Q, R) потенциально в том и только том случае, если его компоненты удовлетворяют условиям ∂P/∂y = ∂Q/∂x, ∂Q/∂z = ∂R/∂y, ∂R/∂x = ∂P/∂z, но эти три условия означают не что иное, как равенство нулю всех трех компонент ротора поля  .
.
Таким образом, для того чтобы векторное поле  было потенциальным, необходимо и достаточно, чтобы выполнялось условие rot
было потенциальным, необходимо и достаточно, чтобы выполнялось условие rot  ≡ 0.
≡ 0.
Вычисление показывает, что для любого векторного поля  div(rot
div(rot  ) ≡ 0, т.е. векторное поле, представимое в виде ротора какого-либо другого векторного поля, соленоидально. Всякому полю
) ≡ 0, т.е. векторное поле, представимое в виде ротора какого-либо другого векторного поля, соленоидально. Всякому полю  , удовлетворяющему условию div
, удовлетворяющему условию div  =0 можно подобрать поле
=0 можно подобрать поле 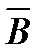 так, что
так, что  = rot
= rot 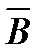 . Векторное поле
. Векторное поле 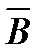 определяется не однозначно, а с точностью до произвольного слагаемого grad U.
определяется не однозначно, а с точностью до произвольного слагаемого grad U.
Если  = rot
= rot 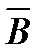 , то поле
, то поле 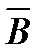 называется вектор – потенциаломполя
называется вектор – потенциаломполя  . Можно доказать, что всякое векторное поле
. Можно доказать, что всякое векторное поле  представимо в виде
представимо в виде  =
= 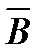 +
+ 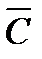 , где
, где 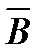 потенциально, а
потенциально, а 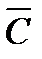 соленоидально.
соленоидально.
Оператор Гамильтона
Выше было введено понятие градиента скалярного поля. Переход от скалярного поля U к grad U можно рассматривать как некоторую операцию, которую обозначают символом V (читается «набла») и называют оператором «набла» или оператором Гамильтона. Таким образом, по определению V =grad U.
Оператор V удобно трактовать как символический вектор с компонентами: V = i∂ /∂x + j∂ /∂y + k∂ /∂z. Применение его к скалярной функции – как умножение скаляра на этот вектор. С помощью вектора V удобно записывать и остальные операции векторного анализа, а именно, если
 = (Р, Q, R), то div
= (Р, Q, R), то div  = ∂P/∂x + ∂Q/∂y+∂R/∂z = (V,
= ∂P/∂x + ∂Q/∂y+∂R/∂z = (V,  ), т.е. дивергенция векторного поля
), т.е. дивергенция векторного поля 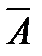 есть скалярное произведение символического вектора V и вектора
есть скалярное произведение символического вектора V и вектора 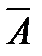 . Аналогично rot
. Аналогично rot  = (∂R/∂y - ∂Q/∂z)i + (∂P/∂z - ∂R/∂x)j + (∂Q/∂x -∂P/∂y)k = [V,
= (∂R/∂y - ∂Q/∂z)i + (∂P/∂z - ∂R/∂x)j + (∂Q/∂x -∂P/∂y)k = [V,  ], т.е. ротор векторного поля
], т.е. ротор векторного поля  есть векторное произведение вектора V на вектор
есть векторное произведение вектора V на вектор  .
.
Действия с вектором V
Необходимость введения символического вектора V состоит в том, что с его помощью удобно получать и записывать различные формулы векторного анализа.
Рассмотрим два равенства: rot grad U = 0 и
div rot  = 0. Переписав их с помощью вектора V, получим [V, VU] = 0 и (V, V,
= 0. Переписав их с помощью вектора V, получим [V, VU] = 0 и (V, V,  ) = 0.
) = 0.
Аналогия между символическим вектором V и «настоящими» векторами не полная. Формулы, содержащие символический вектор V, аналогичны обычным формулам векторной алгебры в том случае, если они не содержат произведений переменных величин (скалярных или векторных), до тех пор, пока нам не приходится применять входящие в V операции дифференцирования к произведению переменных величин. Если же некоторое выражение содержит произведение двух или более переменных сомножителей, применяя к этому выражению вектор V, нельзя использовать обычные правила векторной алгебры. Пусть U = U(x, у, z) – скалярное поле и  =
=  (x, у, z) – векторное поле. Вычислим div (U
(x, у, z) – векторное поле. Вычислим div (U  ), т.е. (V, U
), т.е. (V, U  ).
).
Применение вектора V сводится к применению входящих в него операций дифференцирования.
Дадим сводку формул, связывающих операции взятия градиента, ротора и дивергенции с основными операциями векторной алгебры:
1. div(U  ) = (
) = (  , grad U)+ U div
, grad U)+ U div  ;
;
2. grad (UW) = W grad U + U grad W;
3. rot (U  ) = U rot
) = U rot  + [grad U,
+ [grad U,  ];
];
4. div[  ,
, 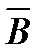 ] = (
] = ( 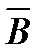 , rot
, rot  ) — (
) — (  , rot
, rot 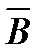 );
);
5. rot[  ,
, 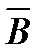 ] = (
] = ( 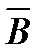 , V)
, V)  -(
-(  , V)
, V) 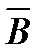 +
+  div
div 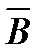 -
- 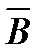 div
div  ;
;
6. grad (  ,
, 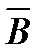 ) = (
) = ( 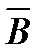 , V)
, V)  + (
+ (  , V)
, V) 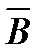 + [
+ [ 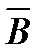 , rot
, rot  ] + + [
] + + [  , rot
, rot 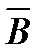 ].
].
Дата: 2016-10-02, просмотров: 295.