Площади плоских фигур.
Площадь в прямоугольных координатах.
Если площадь S ограничена двумя непрерывными
Кривыми y1=f1(x) и y2=f2(x) и двумя вертикалями х=а
и x=b, где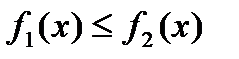 
при 
,
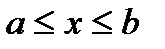то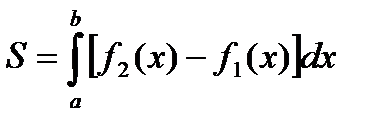 
.
Площадь, ограниченная кривой, заданной в
Параметрическом виде.
Если кривая в параметрическом виде x=x(t),y=y(t),
то площадь криволинейной трапеции, ограниченной
этой кривой, двумя вертикалями, соответствующими
x=a, x=b и отрезком оси ОХ, выражается интегралом
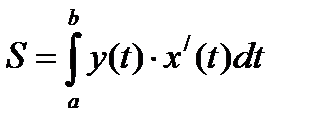, где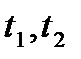 
определяются из уравнений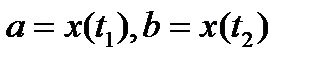 
( 
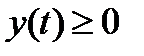на [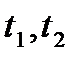 
] ).
Площадь в полярных координатах.
Площадь, ограниченная непрерывной кривой
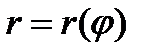и двумя полярными радиусами 
.Равна 
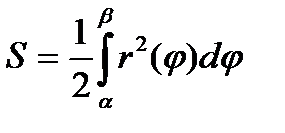
Длина дуги кривой.
Длина дуги в прямоугольных координатах
Длина дуги гладкой (непрерывно дифференцируемой)
кривой y=f(x), содержащейся между точками с абсциссой
x=a и x=b, равна
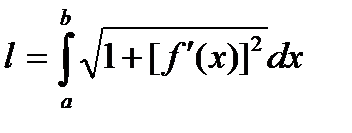
Длина дуги кривой, заданной параметрически
Если кривая задана уравнениями в параметрической
форме x=x(t), y=y(t), где x(t) и y(t) непрерывно
дифференцируемые функции, то длина дуги равна
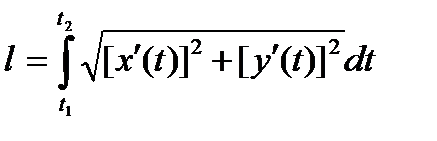,где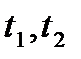 
- значения параметра, соответствующие концам дуги;
Длина дуги в полярных координатах
Если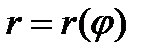 
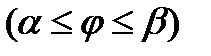, то
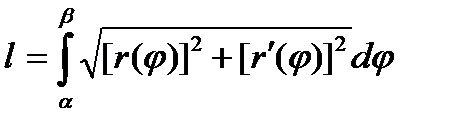
Объёмы тела.
Объём тела вращения
Объёмы тел, образованных вращением криволинейной
трапеции, ограниченной кривой y=f(x), осью ОХ и
двумя вертикалями x=a и x=b, вокруг осей ОХ и OY,
выражаются соответственно формулами
.
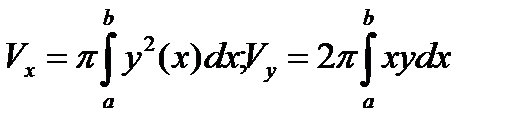Объём тела, образованного вращением вокруг оси OY
фигуры, ограниченной x=g(y), осью OY и двумя
параллелями y=c и y=d определяется по формуле
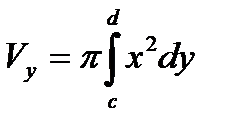
Если кривая задана параметрически или в полярных координатах, то в приведённых формулах нужно сделать замену
переменной интегрирования. Объём тела, полученного при вращении сектора, ограниченного дугой кривой
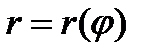и полярными радиусами 
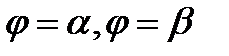вокруг полярной оси 
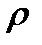равен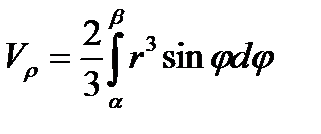 
Вычисление объёмов тел по известным
Поперечным сечениям
Если S(x) – площадь сечения тела плоскостью,
перпендикулярной к оси ОХ в точке абсциссой х, то объём этого тела равен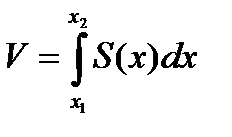 
, где х1, х2 – абсциссы крайних точек сечения тела.
Пример 1.Найти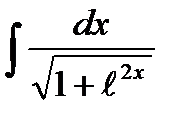 
.
Решение. Так как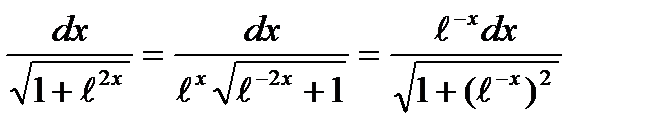 
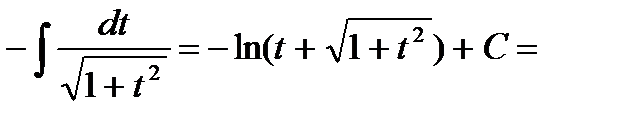
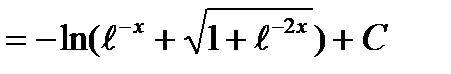.Здесь замена переменной 
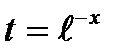приводит к табличному интегралу.
Пример 2. Найти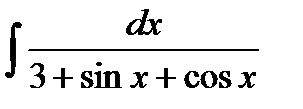 
.
Решение. Подынтегральная функция является функцией от sin x и cos x. Применим подстановку
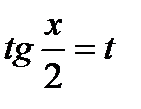. При этом 
.
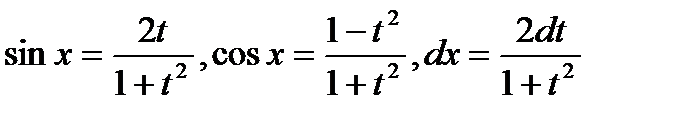Тогда
.
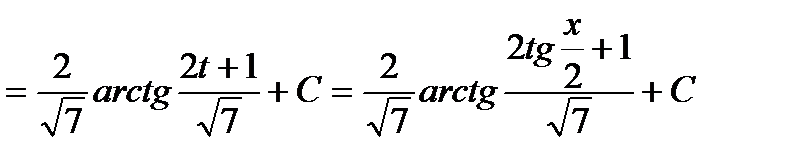Преобразование, произведённое в знаменателе,
называется выделением полного квадрата:
.
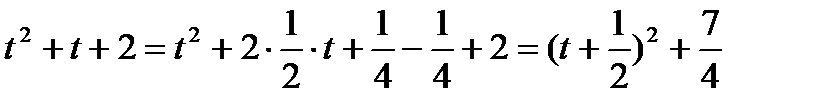Пример 3. Найти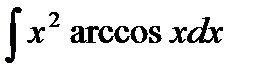 
.
Решение. Применим метод интегрирования по
частям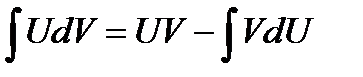 
, где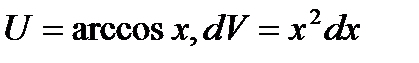 
. Находим
.
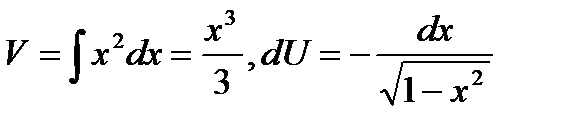Получим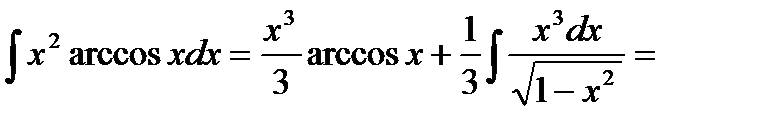 
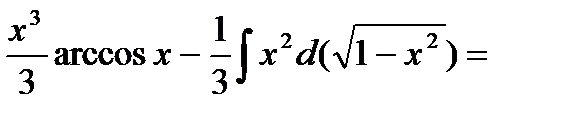
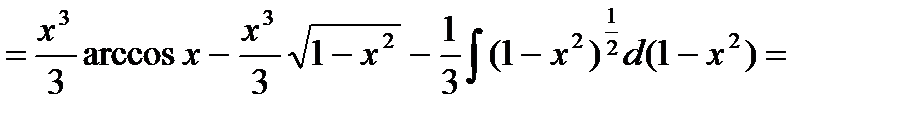
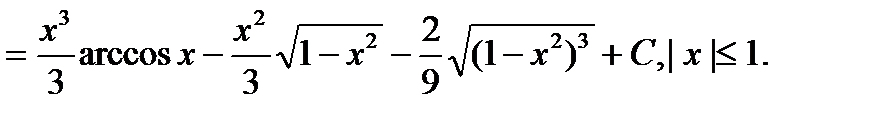
Пример 4. Найти интеграл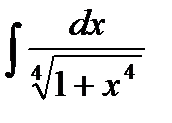 
.
Решение. Перепишем интеграл в виде
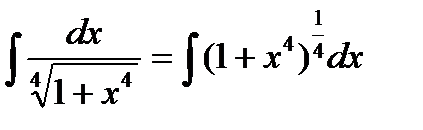, откуда следует, что это интеграл от дифференциального бинома при m=0, n=4, p=-1/4. Так как 
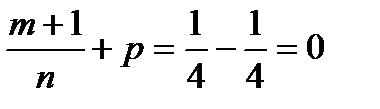, то имеем третий случай интегрируемости. Подстановка 
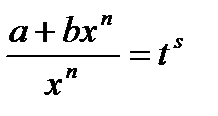, где s - знаменатель
p в данном случае примет вид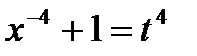 
, откуда
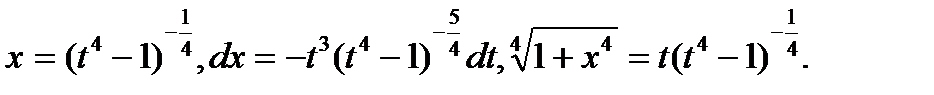
Следовательно
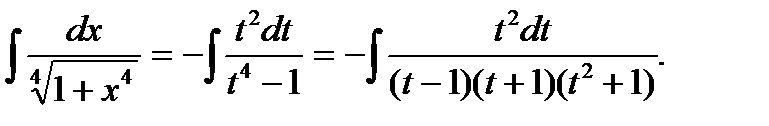
Подынтегральная функция является правильной
рациональной дробью. Разложим её на простейшие
дроби
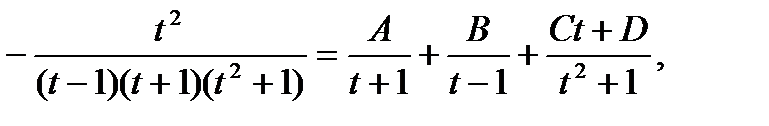откуда
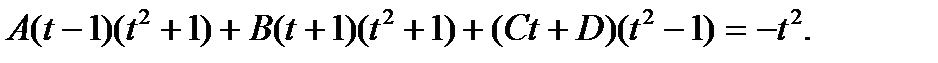
Полагая последовательно t=1 и t=-1, получим
В(1+1)(1+1)=-1, 4В=-1, В=-1/4;
А(-1-1)((-1)(-1)+1)=-(-1)(-1), -4А=-1, А=1/4.
Неопределённые коэффициенты C и D можно
найти, приравнивая коэффициенты при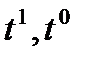 
в
тождестве слева и справа, получим
А+В-С=0, С=0, -А+В-D=0, D=-1/2.
Следовательно
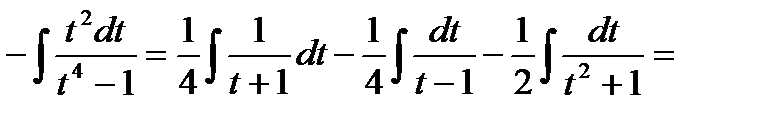
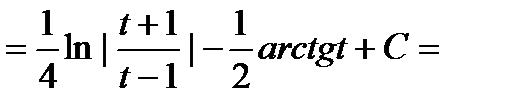
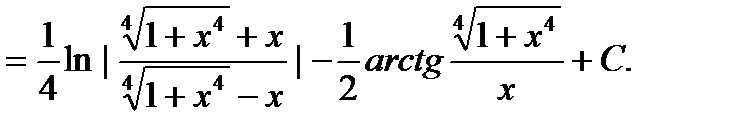
Пример 5.Найти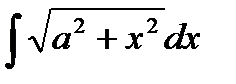 
.
Решение. Применим гиперболическую подстановку
x=a sht, dx=a cht dt,
получим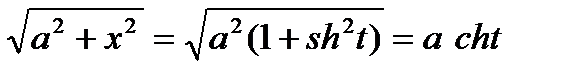 
.
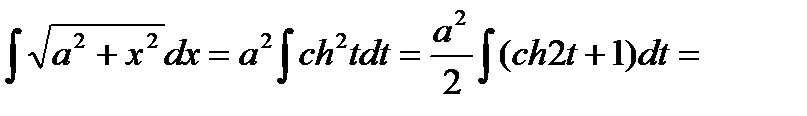
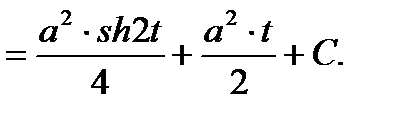Можно получить
.
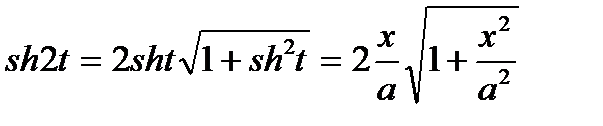Из равенства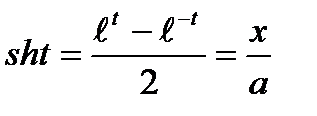 
находим,
что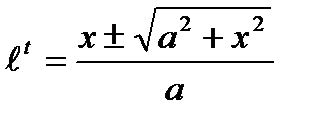 
.
Поскольку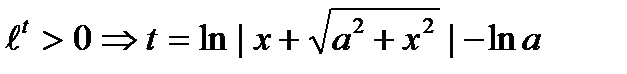 
.
Поэтому окончательно получаем
,
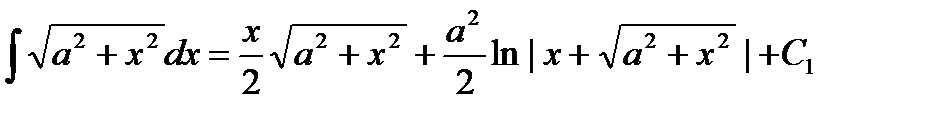где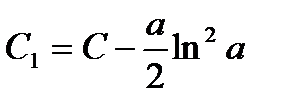 
- новая произвольная постоянная.
Пример 6.Найти площадь фигуры, ограниченной эллипсом x=a cost, y=b sint (рис.20.1).
Решение. Эллипс задан в параметрическом виде.
В силу симметрии эллипса достаточно найти площадь S1 одной его четверти (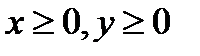 
). Если х изменяется в пределах от 0 до а, то параметр t изменяется в пределах от 
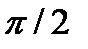до 0, которые находятся из уравнений a cost=0, 
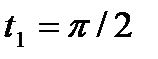; a cost=a, cost=1, t2=0. По формуле для вычисления площади кривой, получим: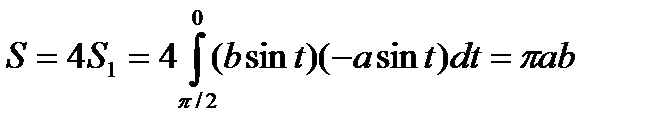 
Рис.20.1
Пример 7.Найти длину дуги кардиоиды r=a(1-cos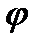 
).
Решение. Кривая (рис.20.2) задана в полярных координатах. В силу её симметрии относительно полярной оси достаточно вычислить длину L, её половины, при этом полярный угол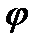 
изменяется от 
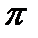до 0. По формуле для вычисления дуги кривой в полярных координатах имеем
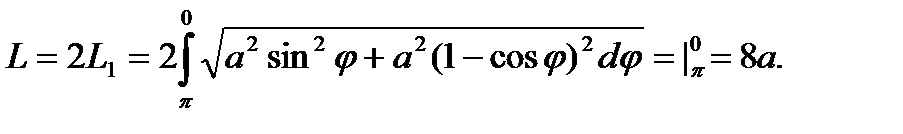
Рис. 20.2
Пример 8.Найти объём тела, полученного вращением
фигуры, ограниченной линиям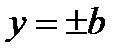и 
и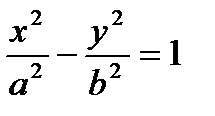 
вокруг оси OY (cм. рис. 20.3).
Решение. Воспользуемся формулой для вычисления
объёма тела вращения.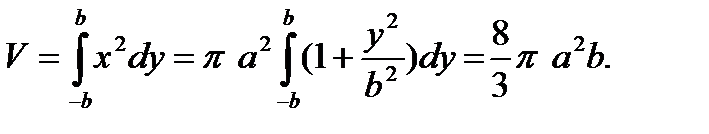 
Рис. 20.3
Пример 9.Найти объём эллипсоида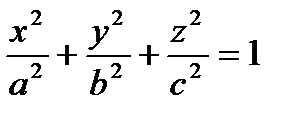 
(рис.20.4)
Решение. В общем случае, когда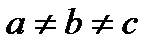 
эллипсоид нельзя считать телом вращения. Поэтому его объём надо вычислять с помощью формулы объёма тела по известным площадям поперечных сечений. Поперечные сечения эллипсоида плоскостями, параллельными оси ОХ, являются эллипсами, уравнения которых имеют вид 
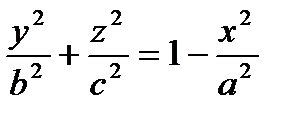или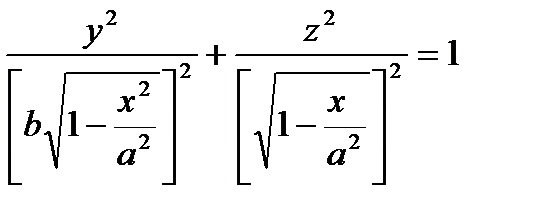 
, поэтому полуоси эллипса, находящегося в сечении плоскостью х=х, равны соответственно
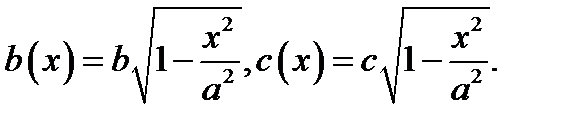Известно, что площадь эллипса с полуосями b и с вычисляется по формуле 
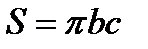. Следовательно, площадь поперечного сечения 
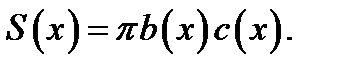Теперь получим
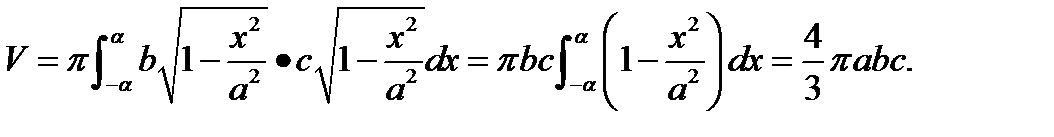
В частности при а=b=c=R получаем формулу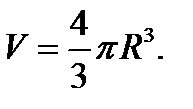 
Рис. 20.4
Пример 10.Вычислить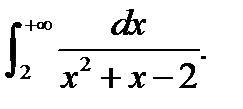 
Решение.Это несобственный интеграл с бесконечным верхним пределом. Так как подынтегральная дробь разлагается на
простейшие дроби вида: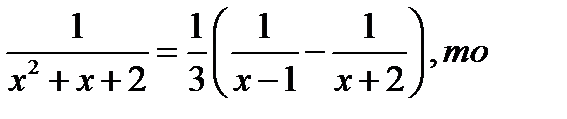 
то 
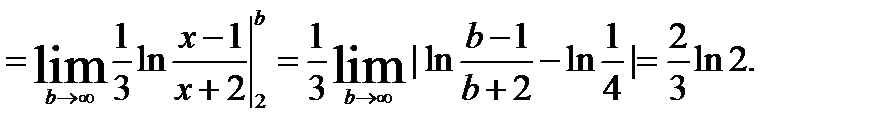
Пример 11..Исследовать сходимость интеграла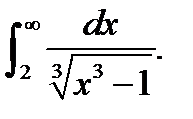 
Решение. Воспользуемся признаком сходимости для несобственных интегралов 1-го рода в виде неравенства. Очевидно, что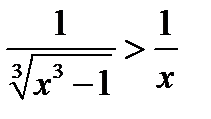 
при x>2. Вычислим
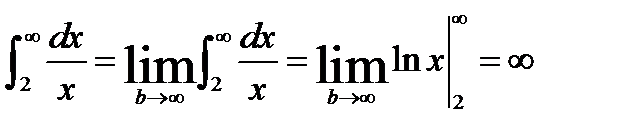- расходится.
Пример 12.Исследовать на сходимость несобственный
интеграл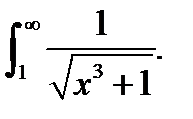 
Решение. При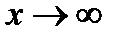 
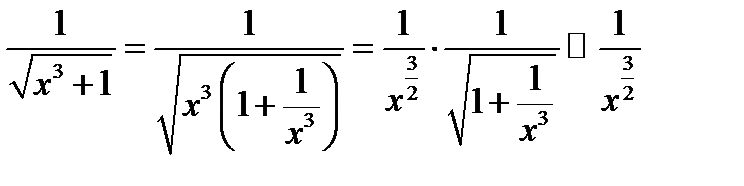
Так как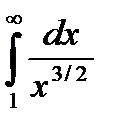 
сходится, то сходится и исходный интеграл
по следствию из признака сходимости для несобственных интегралов 1-го рода.
Пример 13.Вычислить интеграл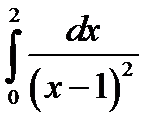 
Решение. Здесь подынтегральная функция имеет
разрыв при x=1.Это несобственный интеграл от
неограниченной функции (2-го рода). По определению
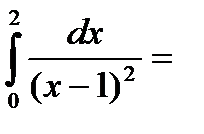
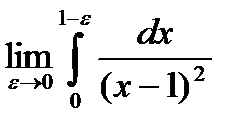
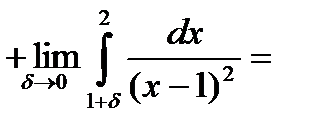
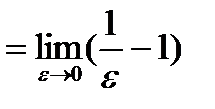
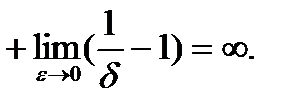Значит данный интеграл расходится.
Пример 14.Исследовать сходимость интеграла 
.
Решение. В данном случае подынтегральная функция имеет разрыв при x=1. воспользуемся признаком сходимости несобственных интегралов 2-го рода.
Для сравнения возьмем функцию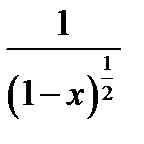 
.
Очевидно, что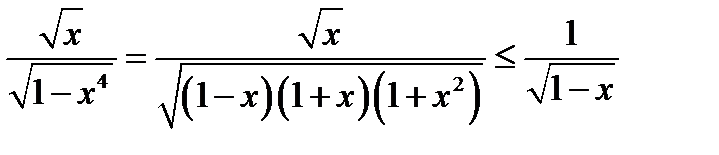 
,
при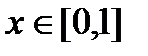 
.
Найдем
.
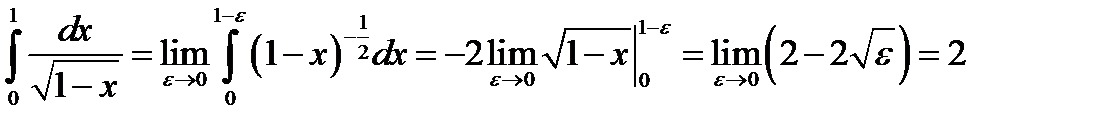Так как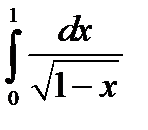 
сходится, то сходится и 
.;
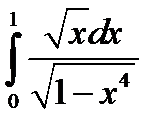Дата: 2016-10-02, просмотров: 317.
