Пределов
Пусть 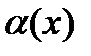 и
и 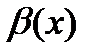 - бесконечно малые функции, при
- бесконечно малые функции, при 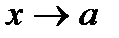 , т.е.
, т.е. 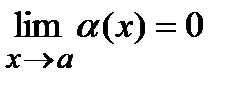 и
и 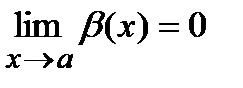 , причем a может быть как числом, так и одним из символов
, причем a может быть как числом, так и одним из символов 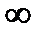 , -
, - 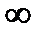 .
.
Бесконечно малые функции 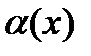 и
и 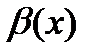 называются бесконечно малыми одного порядка, если предел их отношения
называются бесконечно малыми одного порядка, если предел их отношения 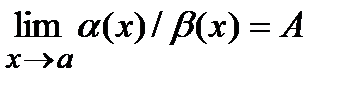 ,
, 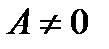 . Если же число А=0, то бесконечно малая
. Если же число А=0, то бесконечно малая 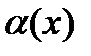 называется бесконечно малой более высокого порядка малости по сравнению с
называется бесконечно малой более высокого порядка малости по сравнению с 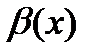 . Если
. Если 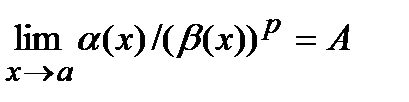 и
и 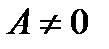 , то бесконечно малая функция
, то бесконечно малая функция 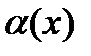 называется бесконечно малой порядка p по сравнению с бесконечно малой функцией
называется бесконечно малой порядка p по сравнению с бесконечно малой функцией 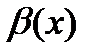 . Бесконечно малые функции
. Бесконечно малые функции 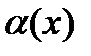 и
и 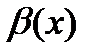 называются эквивалентными,если
называются эквивалентными,если 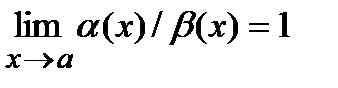 . В этом случае пишут:
. В этом случае пишут: 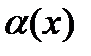 ~
~ 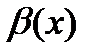 .
.
Теорема(о замене бесконечно малых функций им эквивалентными ). Предел отношения двух бесконечно малых функций не изменяется, если каждую из них или какую-либо одну заменить им эквивалентными функциями.
Если при некотором предельном переходе функция 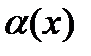 есть бесконечно малая, то Sin(
есть бесконечно малая, то Sin( 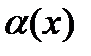 )~
)~ 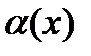 , tg(
, tg( 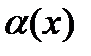 )~
)~ 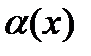 ;
;
arcsin( 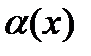 )~
)~ 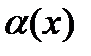 , arctg(
, arctg( 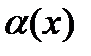 )~
)~ 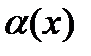 ; ln(1+
; ln(1+ 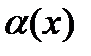 )~
)~ 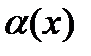 , ln(1+k
, ln(1+k 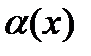 )~k
)~k 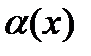 ,
, 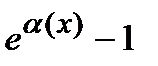 ~
~ 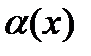 ,
, 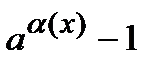 ~
~ 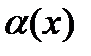 ln a
ln a
Первый замечательный предел
Во многих случаях используется первый замечательный предел 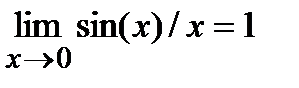 (х- длина дуг или угол, выраженный в радианах) и предполагается известным, что
(х- длина дуг или угол, выраженный в радианах) и предполагается известным, что 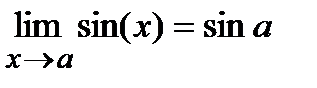 . Иногда при отыскании предела полезно сделать замену переменнойс тем, чтобы упростить вычисление предела и использовать известные пределы. Если пол знаком предела делается замена переменной, то все величины, находящиеся под знаком, должны быть выражены через эту новую переменную. Из равенства, выражающего зависимость между старой переменной и новой, надо определить предельное значение новой переменной. Например, при нахождении предела
. Иногда при отыскании предела полезно сделать замену переменнойс тем, чтобы упростить вычисление предела и использовать известные пределы. Если пол знаком предела делается замена переменной, то все величины, находящиеся под знаком, должны быть выражены через эту новую переменную. Из равенства, выражающего зависимость между старой переменной и новой, надо определить предельное значение новой переменной. Например, при нахождении предела 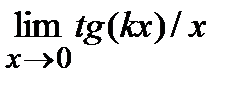 обозначаем t=kx , где при
обозначаем t=kx , где при 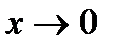 новая переменная
новая переменная 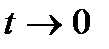 , x=t/k.
, x=t/k.
Тогда
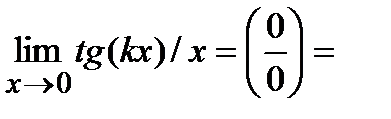
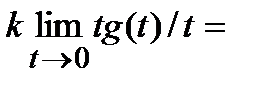
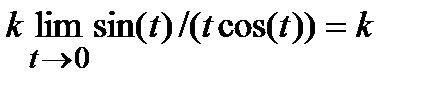
(т.к.cos (0)=1). Полезно помнить, что 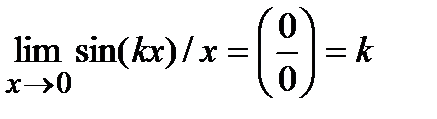 , где k -постоянная величина. Например, при
, где k -постоянная величина. Например, при 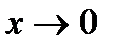 функция sin(x) и tg(x) эквивалентныебесконечно малые, т.е. sin(x)~tg(x); т.к.
функция sin(x) и tg(x) эквивалентныебесконечно малые, т.е. sin(x)~tg(x); т.к. 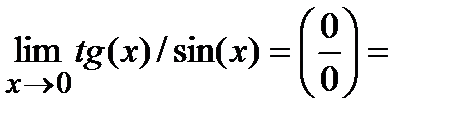
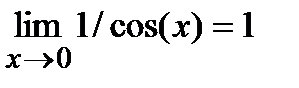 .
.
Пример 1. Найти 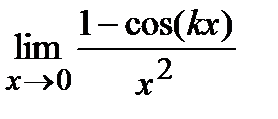
Решение. Применим сначала формулу тригонометрии
1-cos(t)=2sin2(t/2). У нас1-cos(kx)=2sin2(kx/2),при 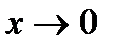 ; sin2(
; sin2( 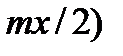 )~(
)~( 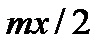 )2. По теореме “замены эквивалентной” получим
)2. По теореме “замены эквивалентной” получим 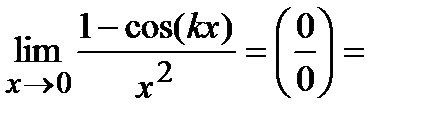
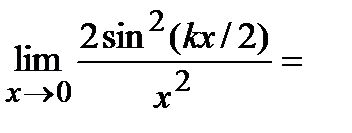
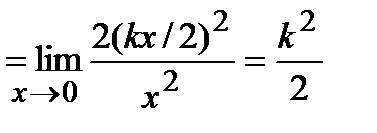 . Заметим, что можно было воспользоваться первым замечательным пределом.
. Заметим, что можно было воспользоваться первым замечательным пределом.
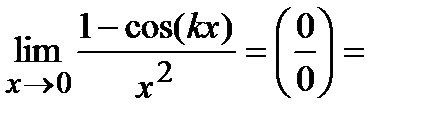
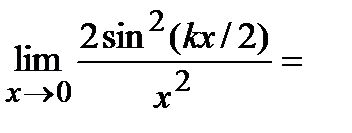
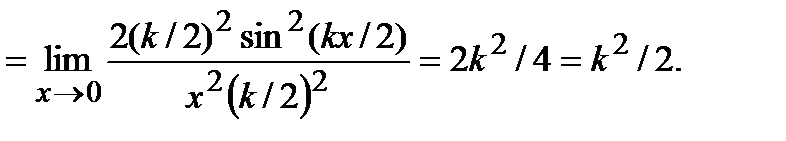 Ответ: k2/2.
Ответ: k2/2.
Пример 2.Вычислить 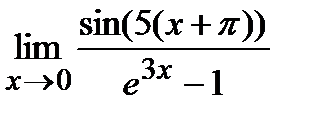
Решение.По формуле тригонометрии sin(5(x+π))=sin(5x+5π)=- sin(5x).
Тогда
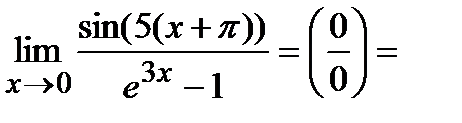
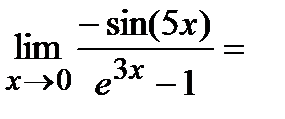
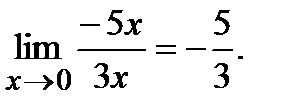
Поскольку при  , sin(5x)~5x, e3x-1~ 3x
, sin(5x)~5x, e3x-1~ 3x
Ответ:-5/3.
Вычисление предела показательно-степенной функции
При нахождении пределов вида 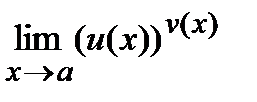 =C
=C
Следует иметь ввиду, что:
1) если существуют конечные пределы
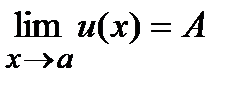 и
и 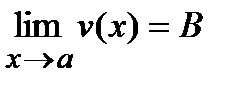 , то C=AB, т.е.
, то C=AB, т.е.
имеет место формула 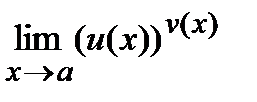
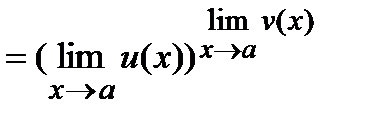
Заметим, что предельное значение а может обозначать и число, и один из символов 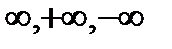 ;
;
2) если 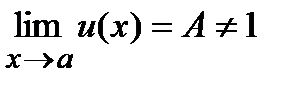 и
и 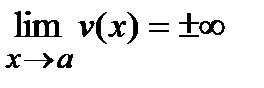 , то вопрос о нахождении
, то вопрос о нахождении 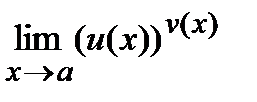 затруднений обычно не вызывает. В том случае полезны иногда формулы:
затруднений обычно не вызывает. В том случае полезны иногда формулы:
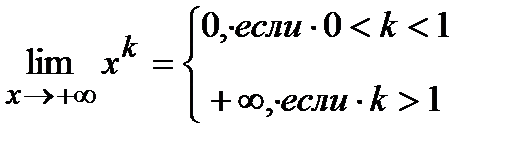 ;
; 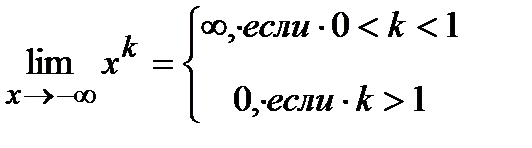
3) если 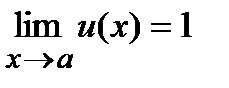 и
и 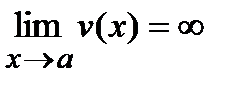 , т.е. имеем неопределенность вида {
, т.е. имеем неопределенность вида { 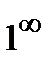 }, то полагают
}, то полагают 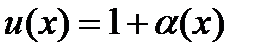 , где
, где 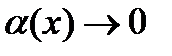 при
при 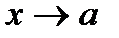 и, следовательно,
и, следовательно,
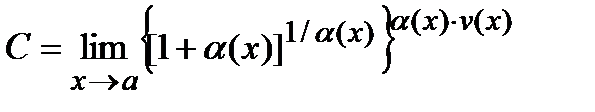
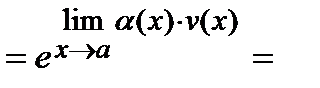
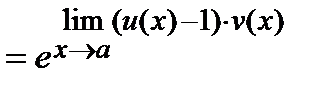
Проиллюстрируем общий прием вычисления пределов на следующем примере ( раскрытие неопределенности вида { 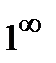 }).
}).
Пример 3.Найти 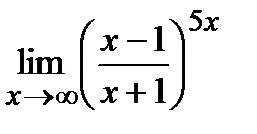
Решение.Здесь основание степени 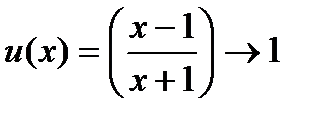 при
при 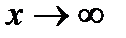 , а показатель степени
, а показатель степени 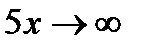 , т.е. имеется неопределенность вида
, т.е. имеется неопределенность вида 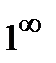 .
.
Тогда 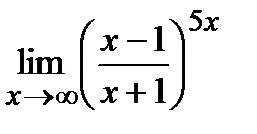
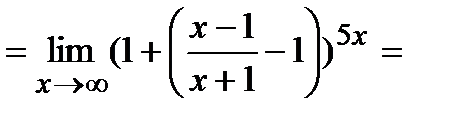
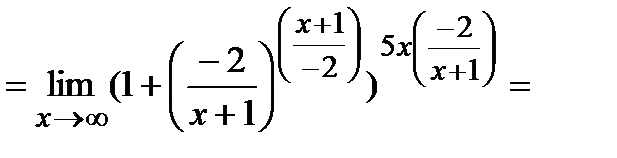
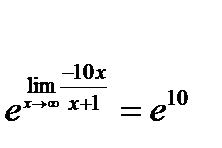
(Получили в качестве 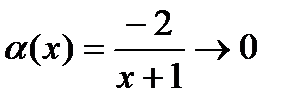 при
при 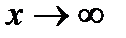 )
)
Замечание 1. При вычислении пределов выражений вида 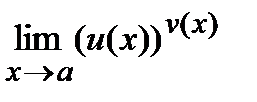 , где
, где 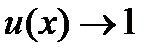 ,
, 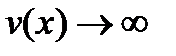 при
при 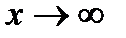 , удобно иногда пользоваться формулой
, удобно иногда пользоваться формулой
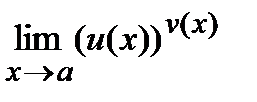
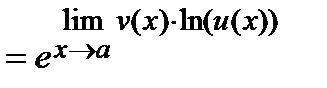 .
.
Замечание 2. При вычислении пределов полезно знать, что
а) если существует и положителен 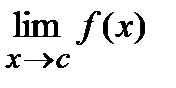 , то
, то
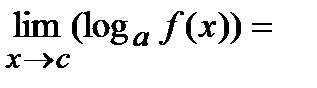
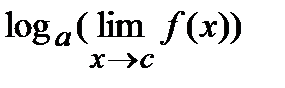 ; б)
; б) 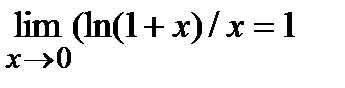 ;
;
в) 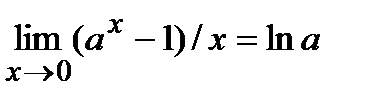 .
.
Производная функции и ее
Вычисление
Если х и х1 – значения аргумента х, а y=f(x) и y=f(x1) - соответственно значения функции y=f(x) , 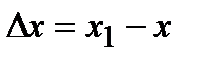 то называется приращением аргумента х на отрезке [x; х1], а
то называется приращением аргумента х на отрезке [x; х1], а
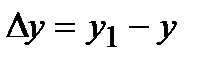 (или
(или 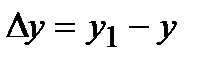 =
= 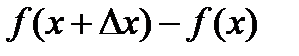 ) называется приращением функции на том же отрезке [x; х1],
) называется приращением функции на том же отрезке [x; х1],
(см. рис. 15.1), где 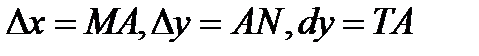 ).
).
Рис.15.1
Отношение 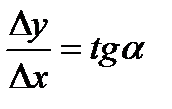 называется средней скоростьюизменения функции y=f(x) на отрезке
называется средней скоростьюизменения функции y=f(x) на отрезке 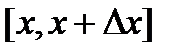 .
.
Производнойфункции y=f(x) в точке x называется предел отношения приращения функции 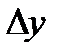 к приращению аргумента
к приращению аргумента 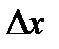 , когда приращение аргумента стремится к нулю:
, когда приращение аргумента стремится к нулю: 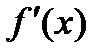 =
= 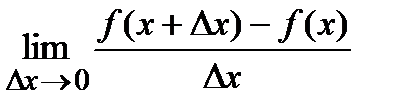 , если этот предел существует.
, если этот предел существует.
Геометрический смысл производной: 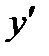 =tg
=tg 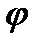 - угловой коэффициент касательной МТ к графику функции y=f(x) в точке х (рис. 15.1).
- угловой коэффициент касательной МТ к графику функции y=f(x) в точке х (рис. 15.1).
Физический смысл производной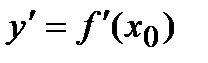 - мгновенная скорость, т.е. скорость изменения функции в данный момент х0. Таким образом, быстрота протекания физических, химических и других процессов выражается с помощью производной. Функция, имеющая конечную производную, называется дифференцируемой.Операция нахождения производной называется дифференцированием.
- мгновенная скорость, т.е. скорость изменения функции в данный момент х0. Таким образом, быстрота протекания физических, химических и других процессов выражается с помощью производной. Функция, имеющая конечную производную, называется дифференцируемой.Операция нахождения производной называется дифференцированием.
Основные правила дифференцирования.
Если 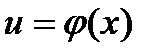 ,
, 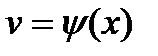 - функции, имеющие производные, c- постоянная величина, то:
- функции, имеющие производные, c- постоянная величина, то:
1) 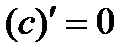 (c=const); 2)
(c=const); 2) 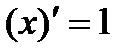 ; 3)
; 3) 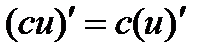 ;
;
4) 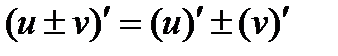 ; 5)
; 5) 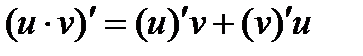 ;
;
6) 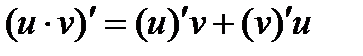 ; 7)
; 7) 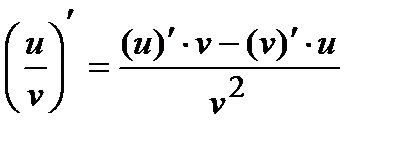 .
.
Производная сложной функции.
Таблица производных
Если 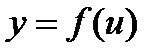 и
и 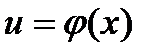 - дифференцируемые функции своих аргументов, то производная сложной функции
- дифференцируемые функции своих аргументов, то производная сложной функции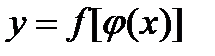 существует и равна произведению производной данной функции y по промежуточному аргументу u на производную промежуточного аргумента u по независимой переменной х:
существует и равна произведению производной данной функции y по промежуточному аргументу u на производную промежуточного аргумента u по независимой переменной х: 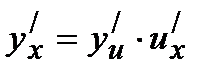 , или
, или 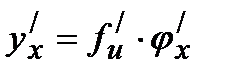 , или
, или 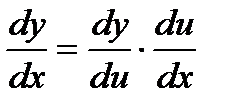 . Это правило распространяется на из любого конечного числа дифференцируемых функций.
. Это правило распространяется на из любого конечного числа дифференцируемых функций.
Таблица производных основных
элементарных функций.
Пусть 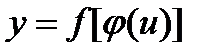 , где
, где 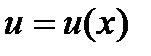 . Тогда:
. Тогда:
1) 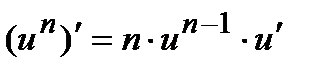 ( n - любое число);
( n - любое число);
2) 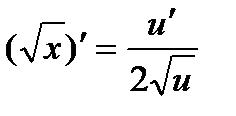 ; 3)
; 3) 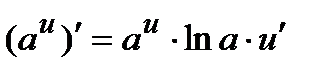 (a>0,
(a>0,  ;
;
4) 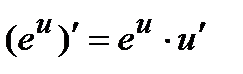 ; 5)
; 5) 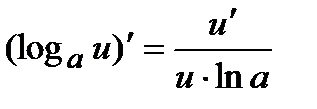 ;
;
6) 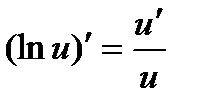 ; 7)
; 7) 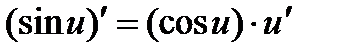 ;
;
8) 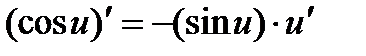 ; 9)
; 9) 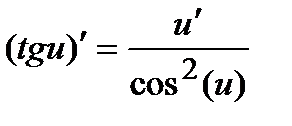 ;
;
10) 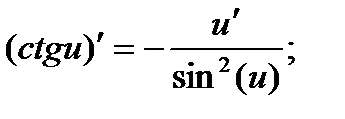 11)
11) 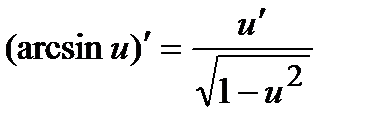 ,(
,( 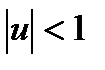 );
);
12) 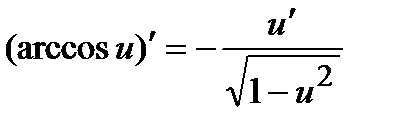 , (
, ( 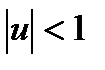 ); 13)
); 13) 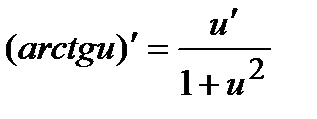 ;
;
14) 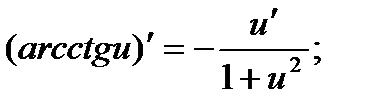 15)
15) 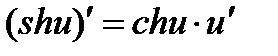 ;
;
16) 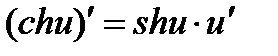 ; 17)
; 17) 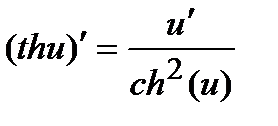 ; 18)
; 18) 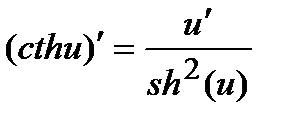 .
.
Замечание. Гиперболические функции определены так:
1) 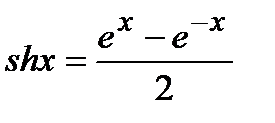 - гиперболический синус
- гиперболический синус
2) 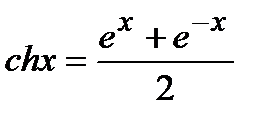 -гиперболический косинус
-гиперболический косинус
3) 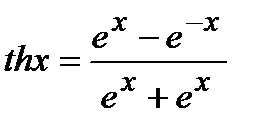 -гиперболический тангенс
-гиперболический тангенс
4) 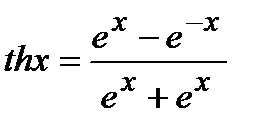 -гиперболический котангенс
-гиперболический котангенс
Для гиперболический функций имеют место формулы, аналогичные фомулам для тригонометрических функций.
Основные формулы:
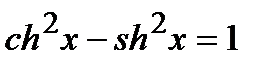 ;
; 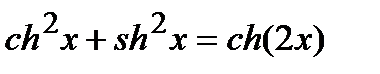 ;
; 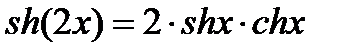 ;
; 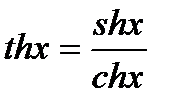 ,
, 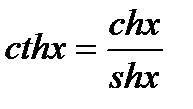 ; и т.д.
; и т.д.
Пример 1. Найти 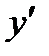 , если
, если 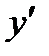 =sin3(x/4).
=sin3(x/4).
Решение. Это сложная функция промежуточным первым аргументом u= sin(x/4) и t=x/4 . Данную функцию можно представить в виде: y=u3 , где u=sin(t); t=x/4 .
Дифференцируя, получаем:
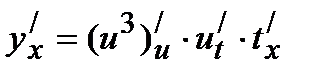 =
=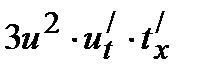 =
=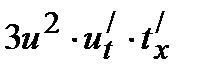 =
=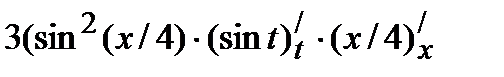 =
= 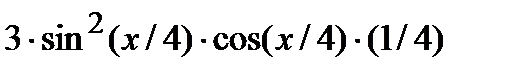 .
.
Уравнение касательной и нормали к плоской кривой
Пусть 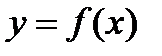 - уравнение плоской кривой,
- уравнение плоской кривой, 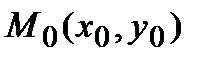 - точка, лежащая на этой кривой, так что
- точка, лежащая на этой кривой, так что 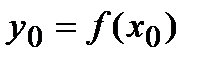 .
.
Уравнение касательной к данной кривой 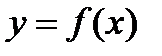 , проходящей через точку касания
, проходящей через точку касания 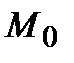 кривой, имеет вид:
кривой, имеет вид:
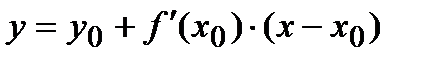 ,
,
где 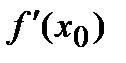 есть угловой коэффициент касательной к данной кривой, проходящей через точку
есть угловой коэффициент касательной к данной кривой, проходящей через точку 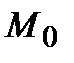 . Иначе говоря, где
. Иначе говоря, где 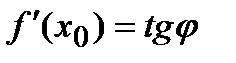 ,
, 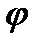 - угол между касательной к кривой , проведенный через точку
- угол между касательной к кривой , проведенный через точку 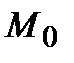 , и промежуточным направлением оси абсцисс .
, и промежуточным направлением оси абсцисс .
Нормалью к кривой в точке 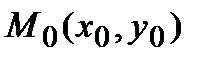 называется перпендикуляр к касательной, проведенный через точку касания. Уравнение нормали к кривой
называется перпендикуляр к касательной, проведенный через точку касания. Уравнение нормали к кривой 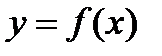 в точке
в точке 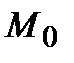 имеет вид:
имеет вид: 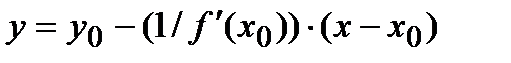 .
.
Пример 2 .Составить уравнение касательной и нормали к кривой y=x3+2x в точке с абсциссой x0=1.
Решение. Найдем производную данной функции и ее значение при x0=1, y /=3x2+2, y /(x0)=y /(1)=3+2=5. Угловой коэффициент касательной 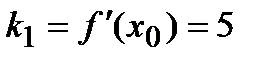 . Вычислим значение функции при x0=1:
. Вычислим значение функции при x0=1: 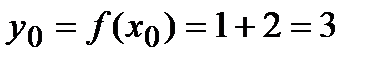 . Следовательно,
. Следовательно, 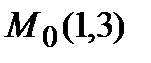 -точка касания и уравнение касательной будет y=3+5(x-1), или 5x-y-2=0; а уравнение нормали y=3-(1/5)(x--1), или x+5y-16=0 , где угловой коэффициент нормали k2=-1/k1, так как условием перпендикулярности двух прямых y=k1x+b1 и y=k2 x+b2 является соотношение:k1 k 2 =-1 Ответ: 5x-y-2=0, x+5y-16=0 .
-точка касания и уравнение касательной будет y=3+5(x-1), или 5x-y-2=0; а уравнение нормали y=3-(1/5)(x--1), или x+5y-16=0 , где угловой коэффициент нормали k2=-1/k1, так как условием перпендикулярности двух прямых y=k1x+b1 и y=k2 x+b2 является соотношение:k1 k 2 =-1 Ответ: 5x-y-2=0, x+5y-16=0 .
Дифференциал функции.
Применение дифференциала
Дифференциалом (первого порядка) функции 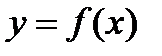 называется главная часть ее приращения, линейная относительно приращения
называется главная часть ее приращения, линейная относительно приращения 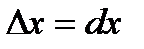 независимой переменной x. Дифференциал функции равен произведению ее производной
независимой переменной x. Дифференциал функции равен произведению ее производной 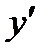 на дифференциал независимой переменной
на дифференциал независимой переменной 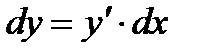 . Отсюда
. Отсюда 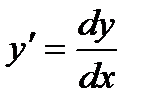 . Если приращение
. Если приращение 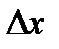 аргумента мало по абсолютной величине, то дифференциал
аргумента мало по абсолютной величине, то дифференциал 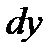 функции
функции 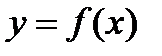 и приращение
и приращение 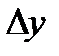 функции приближенно равны между собой
функции приближенно равны между собой 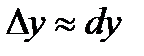 , ибо по определению
, ибо по определению 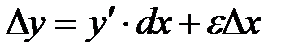 или
или 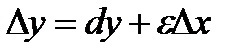 , где
, где 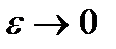 при
при 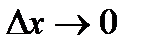 . Иными словами, разность между приращением
. Иными словами, разность между приращением 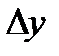 и дифференциалом
и дифференциалом 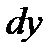 функции есть бесконечно малая высшего порядка. Поэтому при
функции есть бесконечно малая высшего порядка. Поэтому при 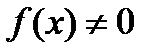 ,
, 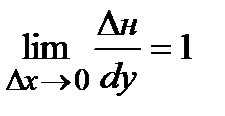 , т.е. приращение функции и ее дифференциал – эквивалентные бесконечно малые. Следовательно,
, т.е. приращение функции и ее дифференциал – эквивалентные бесконечно малые. Следовательно, 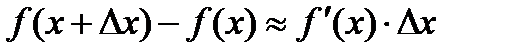 , откуда имеем
, откуда имеем 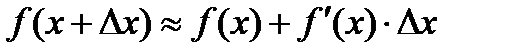 . Последняя формула часто используется в приближенных вычислениях, т.к. позволяет по известному значению функции и ее производной в точке x найти приближенно значение функции в точке
. Последняя формула часто используется в приближенных вычислениях, т.к. позволяет по известному значению функции и ее производной в точке x найти приближенно значение функции в точке 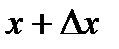 .
.
Пример 1 . Вычислить приближенно arctg1,02, заменяя приращение функции дифференциалом.
Решение.Формула 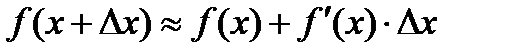 применительно к данной функции f(x)=arctg x перепишем в виде:
применительно к данной функции f(x)=arctg x перепишем в виде: 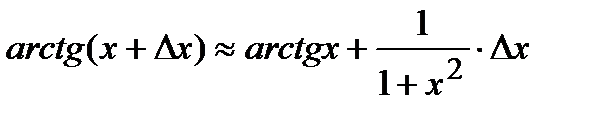 , где
, где 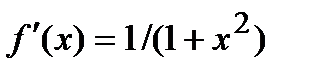 . У нас
. У нас 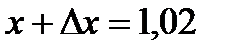 ;x=1;
;x=1; 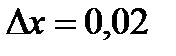 . Подставляя эти значения, получим
. Подставляя эти значения, получим 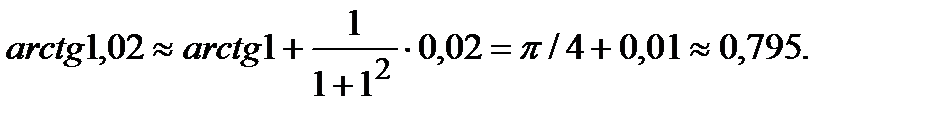
Пример2.Найти дифференциал dy. y= 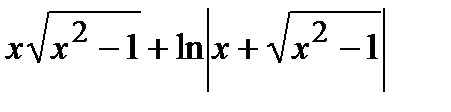
Решение.Имеем 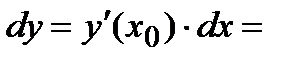
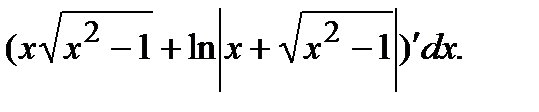
Находим 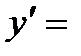
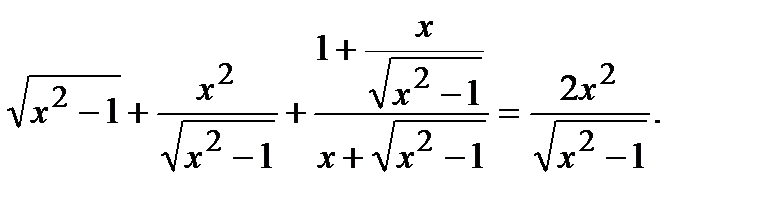
Следовательно, 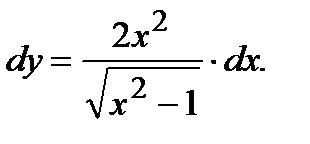 Ответ:
Ответ: 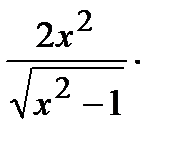
Логарифмическая производная
Логарифмической производнойфункции 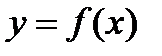 называется производная от логарифма этой функции, т.е.
называется производная от логарифма этой функции, т.е.
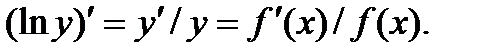 Применение предварительного логарифмирования по основанию e функции иногда упрощает процесс нахождения ее производной. Сначала надо прологарифмировать данную функцию:
Применение предварительного логарифмирования по основанию e функции иногда упрощает процесс нахождения ее производной. Сначала надо прологарифмировать данную функцию: 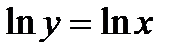 , затем взять производные от обеих частей равенства:
, затем взять производные от обеих частей равенства: 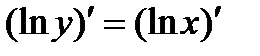 и найти
и найти 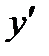 из полученного уравнения. Пусть требуется найти производную от степенно-показательной функции
из полученного уравнения. Пусть требуется найти производную от степенно-показательной функции 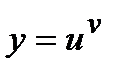 , где
, где 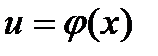 и
и 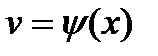 - функции аргумента x . Логарифмируя обе части исходного равенства, получим
- функции аргумента x . Логарифмируя обе части исходного равенства, получим 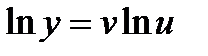 (по свойству логарифма:
(по свойству логарифма: 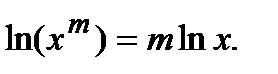 ). Дифференцируя последнее равенство по х, имеем
). Дифференцируя последнее равенство по х, имеем 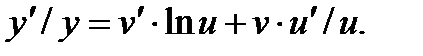 Умножая обе части равенства на y и заменяя затем y через uv, окончательно получаем
Умножая обе части равенства на y и заменяя затем y через uv, окончательно получаем 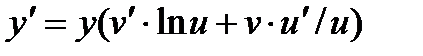 , или после очевидных преобразований:
, или после очевидных преобразований: 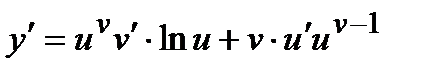
Пример 3. Найти 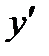 . если
. если 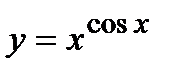 .
.
Решение.Логарифмируя, получим: 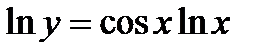 . Дифференцируем обе части получим равенства по х:
. Дифференцируем обе части получим равенства по х: 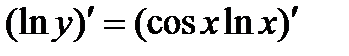 , или
, или 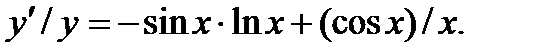 Отсюда
Отсюда 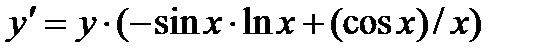 или
или 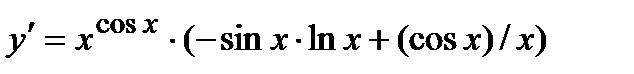 .
.
Замечание.Во многих случаях оказывается выгодным, прежде чем дифференцировать заданную функцию, взять ее логарифм, определить затем производную от этого логарифма и по производной от логарифма отыскать производную от заданной функции. Это так называемый прием логарифмического дифференцирования. К этому приему удобно прибегать при дифференцировании: а) Произведения нескольких функций; б) дроби, числитель и знаменатель которой содержат произведения; в) выражений, содержащих корни из дробей. К нему прибегают всегда при дифференцировании функции вида 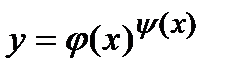 , т.е. когда и основание степени, и показатель степени есть функции от x .
, т.е. когда и основание степени, и показатель степени есть функции от x .
Дифференцирование функций, заданных
параметрически
Пусть функция y аргумента x задана при помощи параметрических уравнений: 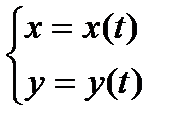 , где t параметр, причем каждому значению соответствует только по одному значению x и y . В механике эти уравнения называются уравнениями движения точки, т.е. линия которую описывает на плоскости движущаяся точка. Например, функция, заданная параметрически:
, где t параметр, причем каждому значению соответствует только по одному значению x и y . В механике эти уравнения называются уравнениями движения точки, т.е. линия которую описывает на плоскости движущаяся точка. Например, функция, заданная параметрически: 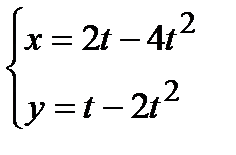 . Представляет собой на плоскости прямую, ибо исключив параметр t из этих уравнений, получим y=x/2 . Однако, практически исключение параметра t из уравнений часто задача трудная, порой просто неразрешимая. Если функций
. Представляет собой на плоскости прямую, ибо исключив параметр t из этих уравнений, получим y=x/2 . Однако, практически исключение параметра t из уравнений часто задача трудная, порой просто неразрешимая. Если функций 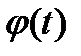 и
и 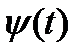 - дифференцируемые и
- дифференцируемые и 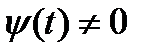 , то производная функции, заданной параметрически, вычисляется по формуле:
, то производная функции, заданной параметрически, вычисляется по формуле: 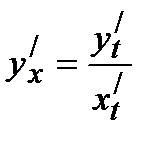 . Или в других обозначениях
. Или в других обозначениях 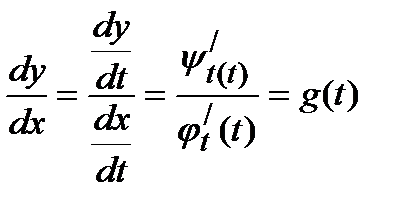 .
.
Вторую производную от y по x находим, дифференцируяпоследнее соотношение
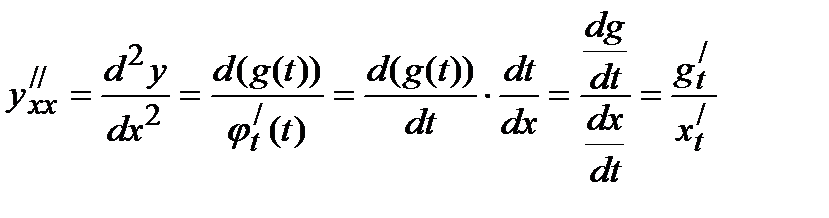
Найти производную 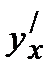 от функции, заданной параметрически.Пример 4 .
от функции, заданной параметрически.Пример 4 . 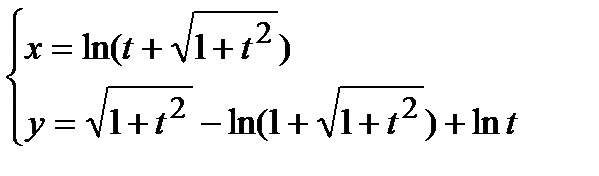
Решение. Находим 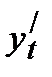 и
и 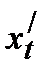 и полученные выражения подставляем в формулу:
и полученные выражения подставляем в формулу:
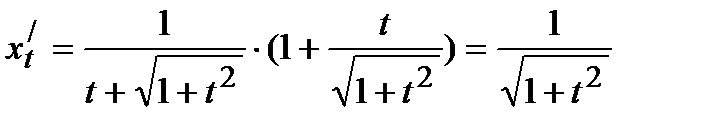 ,
,
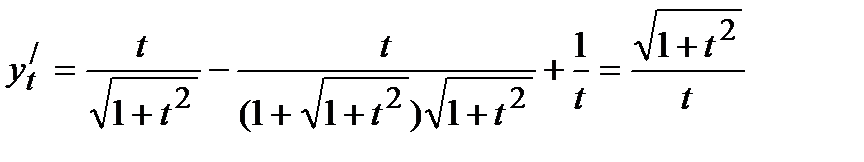 .
.
Получаем 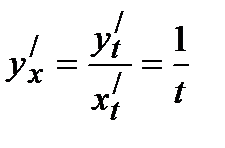 Ответ: 1/t.
Ответ: 1/t.
Пример 5 .Составить уравнение касательной и нормали к кривой в точке при t=0, если 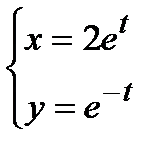
Решение.Последовательно находим: x0=2e0=2; y0=e-0=1,
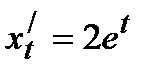 ,
, 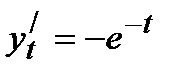 ,
, 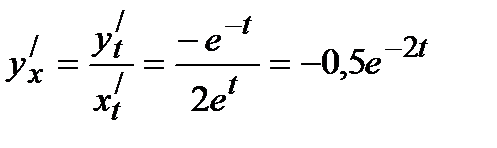 ,
, 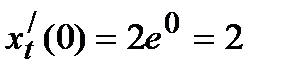 ,
, 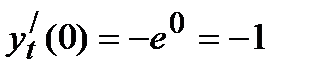 ,
, 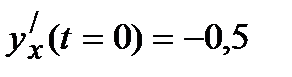 ,M0(2,1).
,M0(2,1).
Как известно, если кривая задана в явном виде y=f(x), то уравнения касательной и нормали в точке M0(x0,y0). имеют соответственно вид: 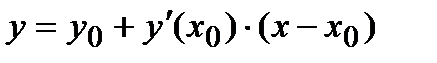 ,
, 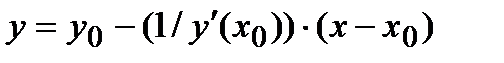 .
.
где y0=f(x0), (y0) /=(f(x0)) /. Поэтому, напишем уравнения касательной и нормали к исходной кривой в точке касания M0(2,1) при t=0 соответственно: y=1-0,5(x-2) , или y=-0,5x+2, или x+2y-4=0 - уравнения касательной; y=1+(1/0,5)(x-2), или
y=2x-3, или 2x-y-3=0 - уравнения нормали.
Производные высших порядков. Формула Лейбница
Производной второго порядка функции y=f(x) называется производная от ее производной 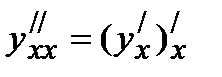 или
или 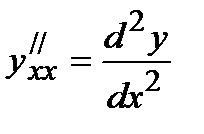 .
.
Механический смысл второй производной: если 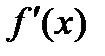 истолковывается как скоростьнекоторого процесса, то
истолковывается как скоростьнекоторого процесса, то 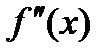 характеризует ускорение того же самого процесса.
характеризует ускорение того же самого процесса.
Аналогично определяются производные третьего, четвертого и других порядков:
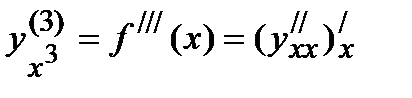 =
= 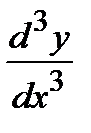 ,
, 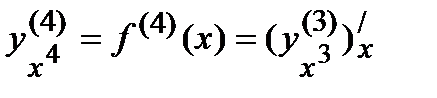 =
= 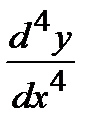 ,…
,…
Вообще, производной n-го порядка, или n-ой производной от функции называется производная от ее (n-1)-го порядка.
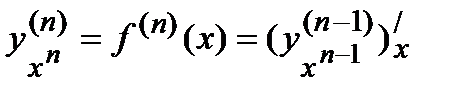 =
= 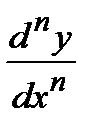 . На практике, иногда удается найти закон, для n-ой производной. При нахождении производной n-го порядка от произведения двух функций u(x) и v(x) можно применять формулу Лейбница:
. На практике, иногда удается найти закон, для n-ой производной. При нахождении производной n-го порядка от произведения двух функций u(x) и v(x) можно применять формулу Лейбница:
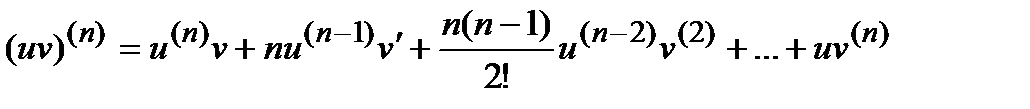 .где биноминальные коэффициенты
.где биноминальные коэффициенты 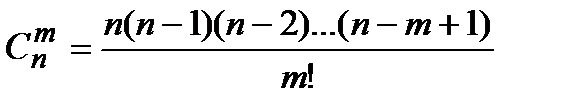 ,
, 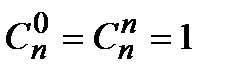 , причем
, причем 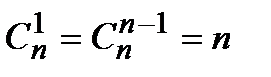 ;
; 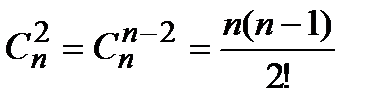 и т.д.
и т.д.
Пример 6.Найти 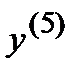 для функции y=x6e3x.
для функции y=x6e3x.
Решение. Применяем формулу Лейбница, полагая u=x6, v=e3x, для случая n=5:
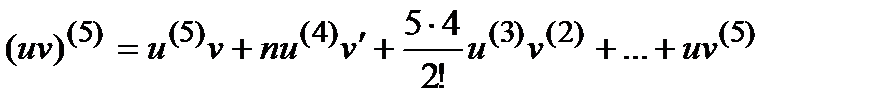
Находим пять производных от каждого из сомножителей :
u /=6x5, u //=30x4, u (3)=120x3, u(4)=360x2, u(5)=720x,
v /=3e3x, v //=9e3x, v (3)=33e3x, v (4)=34e3x v (5)=35e3x..
Подставляя эти производные в формулу Лейбница, получаем
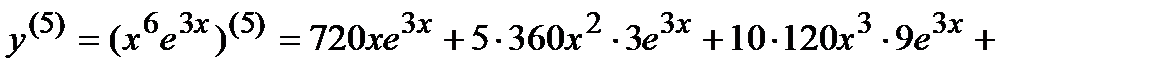
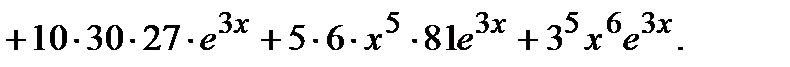
Правило Лопиталя
При раскрытие неопределенностей вида 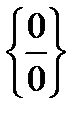 и
и 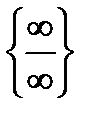 можно
можно
применять правило Лопиталя. Используя теоремы о дифференцируемых функциях (теорему Коши) можно пределы вычислять так: 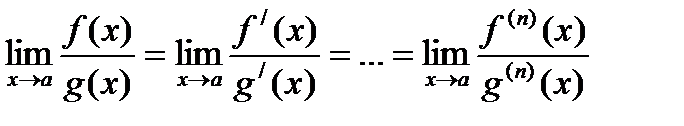 , производные вычисляются до тех пор, пока не исчезнет неопределенность.
, производные вычисляются до тех пор, пока не исчезнет неопределенность.
Пример 1. Найти предел 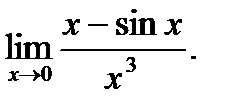
\Решение. 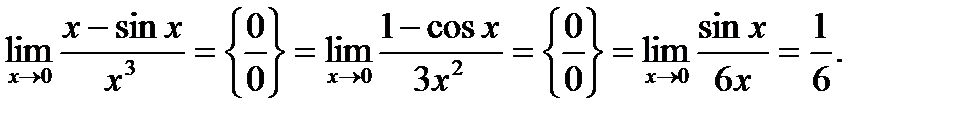
Пример 2.Найти предел 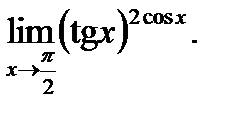
Решение.Это – неопределенность вида 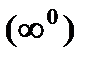 . Положим
. Положим 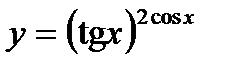 и прологарифмируем:
и прологарифмируем: 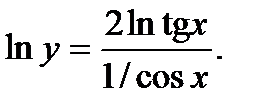
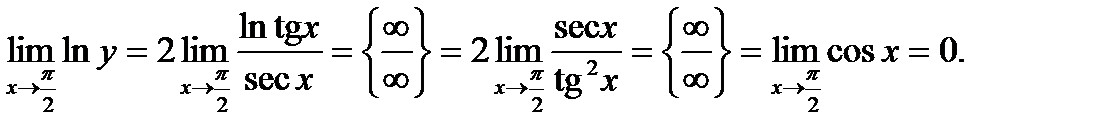
Таким образом 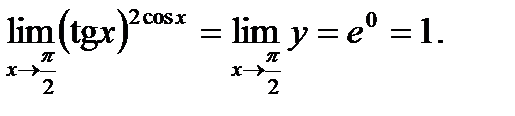
Замечание. Теоремы о дифференцируемых функциях Ролля, Лагранжа, Коши студентам надо разобрать самостоятнльно.
Возрастание и убывание, локальный экстремум функции
Функция 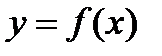 называется возрастающей на некотором интервале (рис.16.1), если для любых значений
называется возрастающей на некотором интервале (рис.16.1), если для любых значений 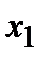 и
и 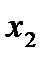 из этого интервала из неравенства
из этого интервала из неравенства 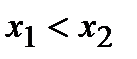 следует неравенство
следует неравенство 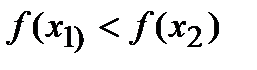 . Если же из неравенства
. Если же из неравенства 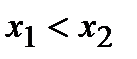 следует нестрогое неравенство
следует нестрогое неравенство 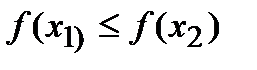 , то функция называется неубывающейна этом интервале.
, то функция называется неубывающейна этом интервале.

Рис. 16.1
Функция называется убывающей(рис.16.2) на некотором интервале, если для любых х1и х2 из этого интервала и неравенства 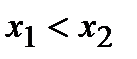 следует неравенство
следует неравенство 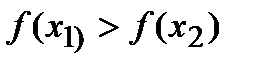 . Если же из неравенства
. Если же из неравенства 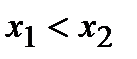 следует нестрогое неравенство
следует нестрогое неравенство 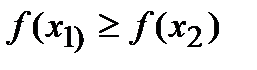 , то функция называется невозрастающей на этом интервале.
, то функция называется невозрастающей на этом интервале.
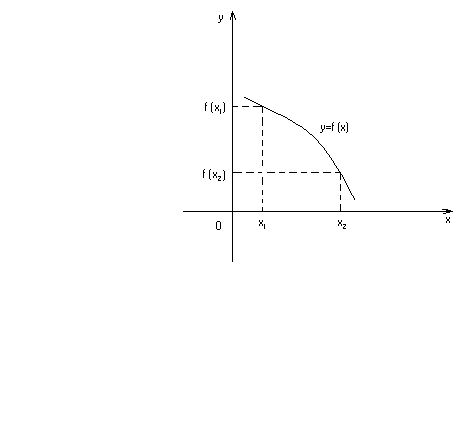
Рис. 16.2
Все выше названные функции называются монотонными.
Достаточное условие возрастания (убывания) функции:
Если функция 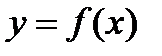 непрерывна на отрезке [a,b] и ее производная
непрерывна на отрезке [a,b] и ее производная 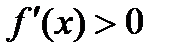 (
( 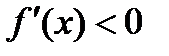 ) при
) при 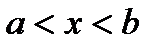 , то функция
, то функция 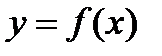 возрастает(убывает) на этом отрезке [a,b]. Говорят, что функция
возрастает(убывает) на этом отрезке [a,b]. Говорят, что функция 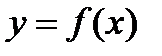 имеет в точке х1 максимум(рис.16.3), если значение функции
имеет в точке х1 максимум(рис.16.3), если значение функции 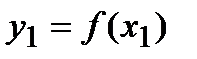 в этой точке больше всех других ее значений во всех точках х, достаточно близкихк точке х1 и отличных от нее, т.е.
в этой точке больше всех других ее значений во всех точках х, достаточно близкихк точке х1 и отличных от нее, т.е. 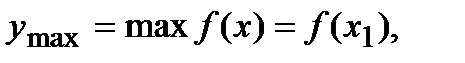 если
если 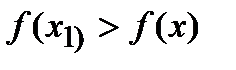 для всякой точки
для всякой точки 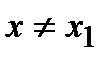 из некоторой окрестности точки х1. Говорят, что функция
из некоторой окрестности точки х1. Говорят, что функция 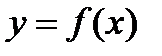 имеет в точке х2 минимум(рис.16.3), если значение функции
имеет в точке х2 минимум(рис.16.3), если значение функции 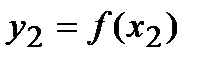 в этой точке меньше всех других ее значений во всех точках х, достаточно близкихк точке х1 и отличных от нее, т.е.
в этой точке меньше всех других ее значений во всех точках х, достаточно близкихк точке х1 и отличных от нее, т.е. 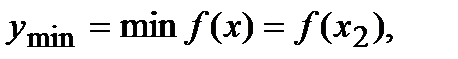 если
если 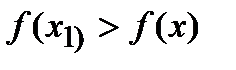 для всякой точки
для всякой точки 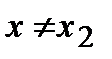 из некоторой окрестности точки x2.
из некоторой окрестности точки x2.
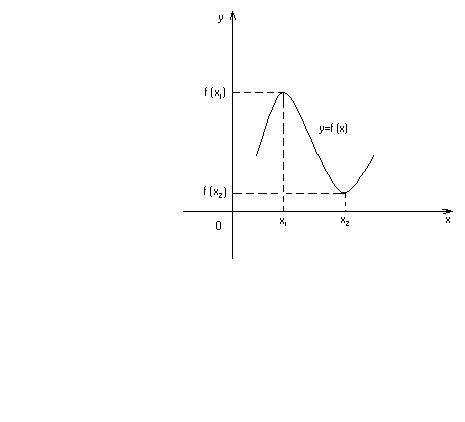
Рис. 16.3
Максимум или минимум функции называется экстремумомфункции. Точки в которых достигается экстремум, называются точками экстремума (максимума или минимума).
Необходимое условие существования экстремума:
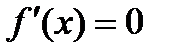 или
или 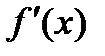 не существуетдля
не существуетдля 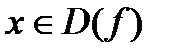 , т.е.
, т.е.
функция может иметь экстремум только в тех точках области определения, где выполняются эти условия. Такие точки называютсякритическими точками1-го рода, т.е. точки, только подозрительные на экстремум.
Достаточные условия существования и отсутствия экстремума непрерывной функции 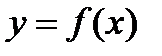 :
:
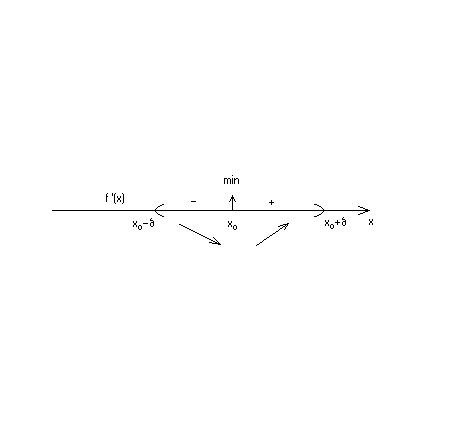
Первое правило. Если производная 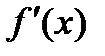 меняет знак при переходе через критическую точку x0 , то точка x0 является точкой экстремума, причем:
меняет знак при переходе через критическую точку x0 , то точка x0 является точкой экстремума, причем:
а) Функция имеет максимум в точкеx0 ,если для 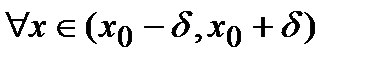 , где
, где 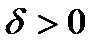 , имеет место
, имеет место
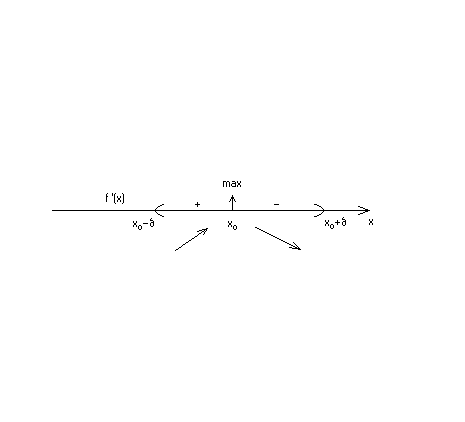
б) Функция имеет минимум в точкеx0 ,если для 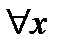 из
из 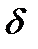 -окрестности
-окрестности 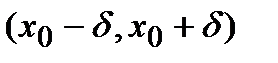 имеет место
имеет место
Если при переходе через критическую точку x0 производная  не меняет знак, то экстремум нет в этой точке:
не меняет знак, то экстремум нет в этой точке:
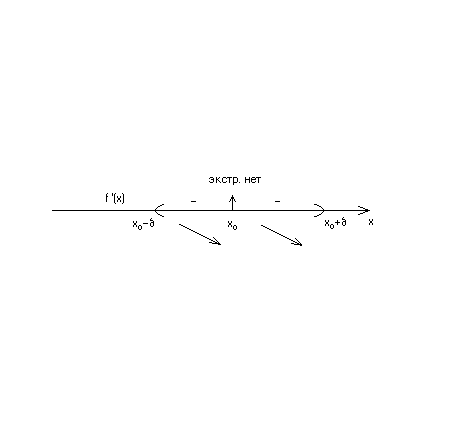
или
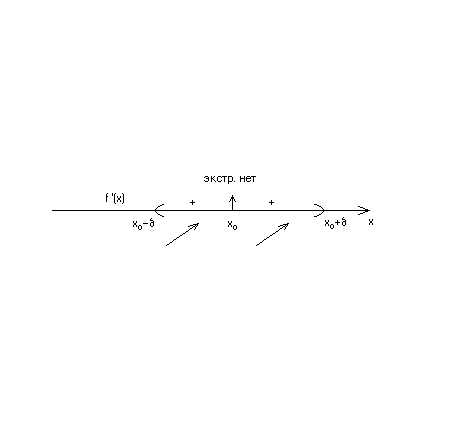
Второе правило. Если в критической точке x0 первая производная 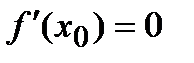 , а вторая производная
, а вторая производная 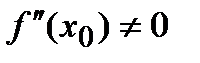 , то точка x0 будет точкой экстремума, причем:
, то точка x0 будет точкой экстремума, причем:
а) если 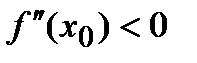 , то x0 - точка максимума;
, то x0 - точка максимума;
б) если 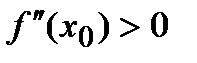 , то x0- точка минимума.
, то x0- точка минимума.
Замечание.В более общем случае, когда первая из не равных нулю в точке x0 производных функции 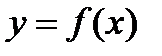 имеет порядок k: Если
имеет порядок k: Если 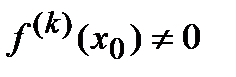 , то если k -четное, то точка x0 является точкой максимума при
, то если k -четное, то точка x0 является точкой максимума при 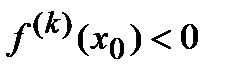 и точкой минимума при
и точкой минимума при 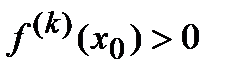 ; если же k -нечетное, то точка x0 является точкой экстремума.
; если же k -нечетное, то точка x0 является точкой экстремума.
Пример 7.
Построить графики функций с помощью производной первого порядка. 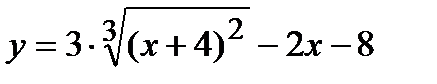
Решение.
1) 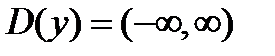 , т.е.
, т.е. 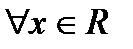 .
.
2) Функция общего вида, т. к.
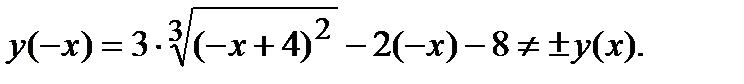
3) Находим точки пересечения графика функции к осям координат: а) с осью oy , x=0 : 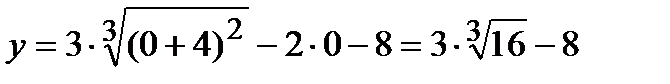 .
.
точка 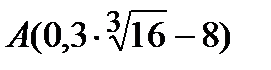 , т.е. y(0)
, т.е. y(0) 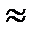 -0,5. б) с осью ox, y=0:
-0,5. б) с осью ox, y=0:
Дата: 2016-10-02, просмотров: 323.