Уравнения кривых второго порядка
Пусть общее уравнение кривой второго порядка
a11x2+a22y2+2a1x+2a2y+a0=0
приведем к каноническому виду: 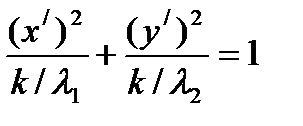 , где
, где 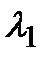 ,
, 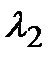 - собственные значения матрицы S . Вычисляем
- собственные значения матрицы S . Вычисляем 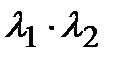
1. если 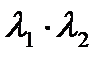 >0, то кривая эллиптического типа;
>0, то кривая эллиптического типа;
2. если 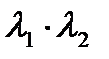 <0 , то кривая гиперболического типа;
<0 , то кривая гиперболического типа;
3. если 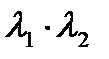 =0, то кривая параболического типа.
=0, то кривая параболического типа.
Исследовать кривую второго порядка и построить ее.
Пример . Дано: K(x,y)= 2x2+2y2-2xy-2x-2y+1=0.
Решение. Имеем a11=2, a22=2, a12=a21=-1; a1=-1, a2=-1, a0=1 . Тогда матрица старших членов 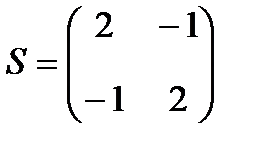 .
.
Составляем характеристическое уравнение
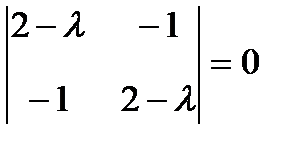 , или
, или 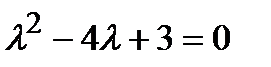 . Корни
. Корни 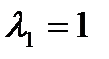 и
и 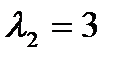 – собственные значения матрицы S. Так как
– собственные значения матрицы S. Так как 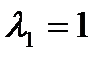 , и
, и 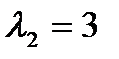 то данная кривая эллиптического типа.
то данная кривая эллиптического типа.
Находим соответствующие им собственные векторы
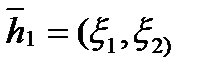 и
и 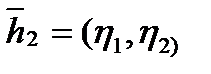 .
.
Для 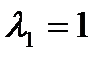 :
: 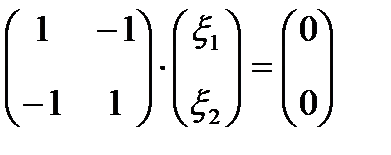 , или
, или 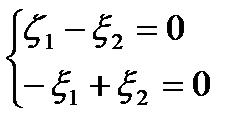 ,
, 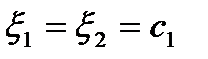 ,
, 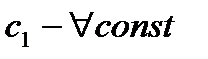 .
.
Пусть c1=1. Тогда 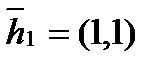 . Нормируем
. Нормируем 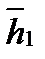 ,
, 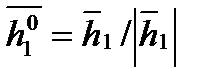 , где
, где 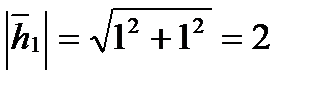 ; получаем
; получаем 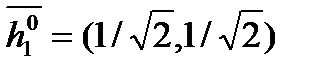 .
.
Для 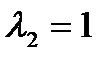 :
: 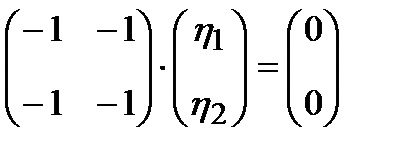 или
или 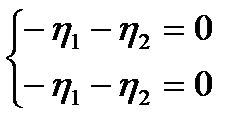 ,
, 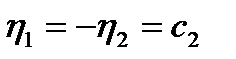 ,
, 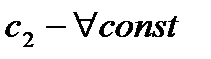 .
.
Пусть с2=1. Тогда 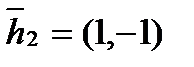 . Нормируем
. Нормируем 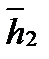 ,
, 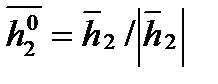 , где
, где 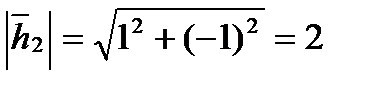 ; получаем
; получаем 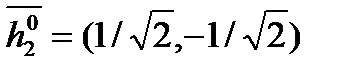 , причем
, причем 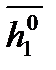
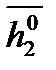 . Орты собственных векторов
. Орты собственных векторов 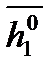 и
и 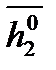 образуют базис в новой системе координат x/,y/. Имеем матрицу Т линейного преобразования координат
образуют базис в новой системе координат x/,y/. Имеем матрицу Т линейного преобразования координат 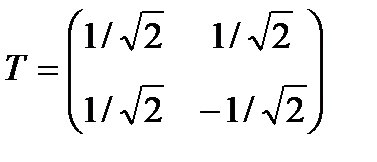
Отсюда получаем формулы преобразования координат
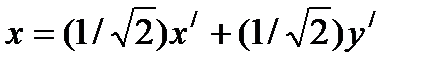 ,
, 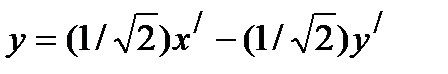 , или
, или
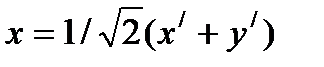 ,
, 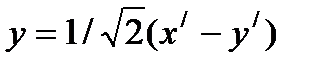 .
.
Подставляем в уравнения кривой найденные выражения для x и y: После раскрытия скобок и приведения подобных получаем (x/)2+3(y/)2-2 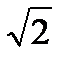 x/+1=0, или (x/)2-2
x/+1=0, или (x/)2-2 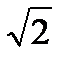 x/+3(y/)2+1=0.
x/+3(y/)2+1=0.
Выделив, полный квадрат имеем: (x/- 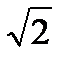 )2+3y/+1=0.
)2+3y/+1=0.
Пусть x//=x/- 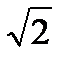 , y//=y/- параллельный перенос координатных осей. Тогда (x//)2+3( y//)2=1,или (x//)2+( y//)2/3=1-каноническое уравнение эллипса в координатах x//, y//, где a =1– большая, b=
, y//=y/- параллельный перенос координатных осей. Тогда (x//)2+3( y//)2=1,или (x//)2+( y//)2/3=1-каноническое уравнение эллипса в координатах x//, y//, где a =1– большая, b= 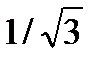 = 0,577 – малая полуоси эллипса (рис.11.1) .
= 0,577 – малая полуоси эллипса (рис.11.1) .
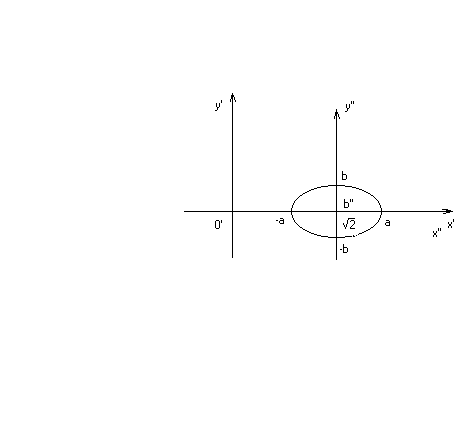
Рис. 11.1
Поверхности второго порядка. Канонические формы
уравнений. Исследование поверхностей второго порядка
методом сечений
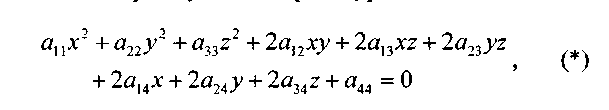
Определение.Поверхностью S второго порядка будем называть геометрическое место точек, декартовы прямоугольные координаты которых, удовлетворяют уравнению вида
в котором, один из коэффициентов
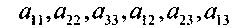
отличен от нуля. Уравнение (*) называется общим уравнением поверхности 2-го порядка.
Очевидно, что поверхность второго порядка как геометрический объект не меняется, если от данной декартовой системы координат перейти к другой декартовой системе координат.
С помощью линейного ортогонального преобразования координат (или параллельного переноса и поворота осей) уравнение вида (*) можно привести к виду
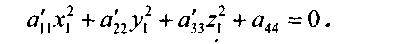
|
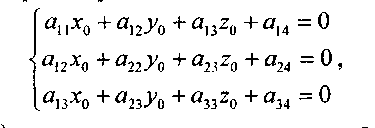
Поверхность S второго порядка называется центральной, если уравнение центра поверхности имеет единственное решение
точка О1 (х0, у0, z0) называется центром поверхности 2-го порядка. Для упрощения будем рассматривать уравнение вида
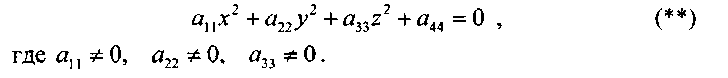
|
Классификация центральных поверхностей
второго порядка
1°. Если коэффициенты а11, а22, а33 одного знака,
а коэффициент а44 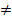 0, то в этом случае поверхность S
0, то в этом случае поверхность S
называется эллипсоидом. Если знак коэффициентов а11,а22, а33 противоположен знаку коэффициента а44, то поверхность
называется вещественным эллипсоидом, в противном случае - мнимым эллипсоидом.
В дальнейшем термином эллипсоид мы будем называть
лишь вещественный эллипсоид.
Каноническое уравнение эллипсоида имеет вид:
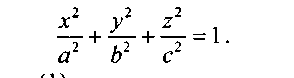
Из уравнения следует, что координатные плоскости являются плоскостями симметрии эллипсоида, а начало координат - центром симметрии. Числа а, b, с называются полуосями эллипсоида и представляют собой длины отрезков от начала до точек пересечения эллипсоида с осями координат. Эллипсоид представляет собой ограниченную поверхность.
Рассмотрим сечения данного эллипсоида плоскостями, параллельными координатной плоскости Оху. Каждая из таких плоскостей определяется уравнением z = h, a линия, которая
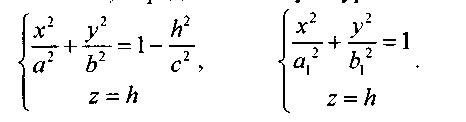
Отсюда следует, что при h < с плоскость z = h пересекает эллипсоид по эллипсу с полуосями
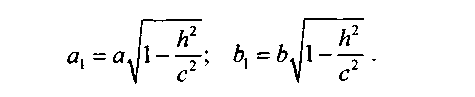
Аналогичнаякартина имеет место при рассмотрении сечений эллипсоида плоскостями, параллельными координатным плоскостям Oxz и Oyz. Сама плоскость Oxz (у =0)
пересекает эллипсоид по эллипсу 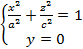
а плоскость Oyz (x = 0) по эллипсу 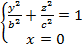
В случае a=b=c, эллипсоид является сферой.
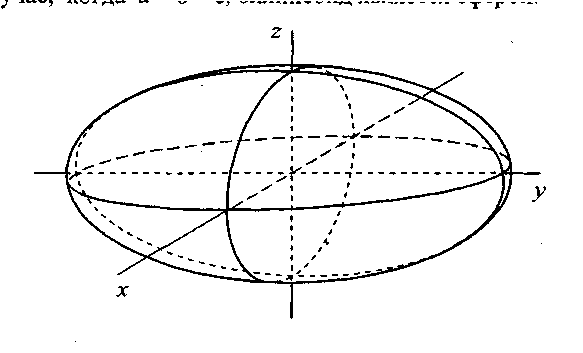
Рис. 11.2
2°. Если из четырех коэффициентов а11,а22, о33, а44 два одного знака, а два других - противоположного, поверхность S называют однополостным гиперболоидом.
Каноническое уравнение однополостного гиперболоида: 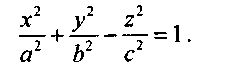
Из уравнения вытекает, что координаты плоскости являются плоскостями симметрии, а начало координат - центром симметрии однополостного гиперболоида.
Рассмотрим его сечение координатной плоскостью Oxz
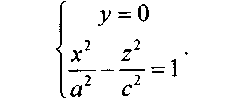
|
Это сечение представляет собой гиперболу, расположенную симметрично относительно координатных осей Ох и Oz и пересекает ось Oz в точках (а, 0, 0), (- а,0, 0).
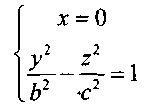
|
Сечение плоскостью Oyz есть гипербола симметричная относительно осей Оу, Oz с точками на оси Oy (0, b, 0), (0, - b, 0).
Рассмотрим сечения данного гиперболоида плоскостями, параллельными плоскости Оху:
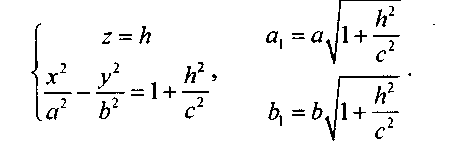
Отсюда видно, что любая плоскость z = h пересекает
гиперболоид по эллипсу 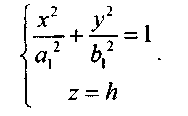
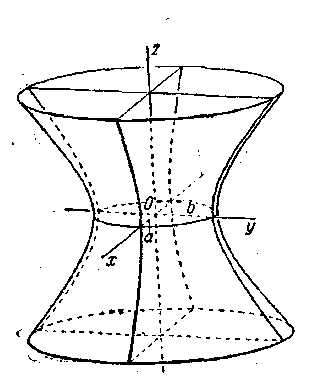
Самых малых размеров эллипс получается в сечении плоскостью z=0 (Oxy) он называется горловым эллипсом.
Однополостный гиперболоид имеет вид бесконечной трубки, расширяющейся в обе стороны от горлового клапана.
|
Рис. 11.3
Величины а, b, с называют ПОЛУОСЯМИ ОДНОПОЛОСТНОГОгиперболоида. В случае а = b уравнение (2') определяет окружность с центром на оси Оx. В этом случае однополостный гиперболоид можно рассматривать как поверхность, образованную вращением гиперболы вокруг одной из осей.
3°. Знак одного из первых трех коэффициентов а11, а22, а33,а44 противоположен знаку остальных коэффициентов. В этом случае поверхность S называется двухполостным гиперболоидом.
Пусть для определенности а11>0, а22 > 0, а33 < 0, а44 >0. Каноническое уравнение двухполостного гиперболоида имеет вид:
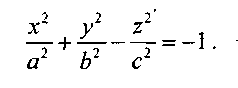
Его сечение плоскостью Oxz определяется уравнениями
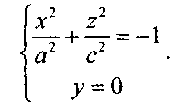
|
Это гипербола, симметричная относительно осей Ох и Oz и пересекающая ось Oz в точках (0,0,c)и(0,0,-с).
Сечение плоскостью Oyz 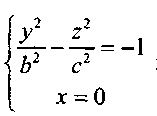 представляет собой
представляет собой
гиперболу, симметричную относительно Оу и Oz и пересекающую Oz в точках (0,0,с) и (0,0, - с).
Сечения данного гиперболоида плоскостями, параллельными координатной плоскости Оху
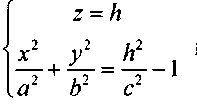
при условии, что 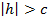 представляет эллипс с полуосями:
представляет эллипс с полуосями:
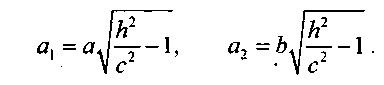
Двухполостный гиперболоид -это поверхность, состоящая из двух отдельных «полостей». Каждая из них имеет вид бесконечной выпуклой чаши.
Величины а,b,с называются полуосями двухполостного гиперболоида.
|
При а=b двухполостный гиперболоид модно рассматривать как поверхность, образованную вращением гиперболы вокруг одной из осей .
Рис. 11.4
4°. Коэффициент a44 = 0. В этом случае поверхность S называется конусом второго порядка. Если коэффициенты а11, а22, а33 одного знака, то левая часть обращается в нуль лишь для х = у = z = 0, то есть уравнению поверхности удовлетворяет одна точка.
В этом случае поверхность называется мнимым конусом. 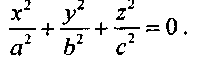
Если коэффициенты а11, а22, а33 имеют разные знаки, то
поверхность S называется вещественным конусом второго порядка. Каноническое уравнение его имеет вид:
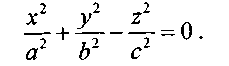
Геометрической особенностью этой поверхности является то, что, если некоторая точка М (отличная от начала координат) лежит на этой поверхности, то все точки прямой, которая проходит через начало координат и точку М, также лежат на этой поверхности.
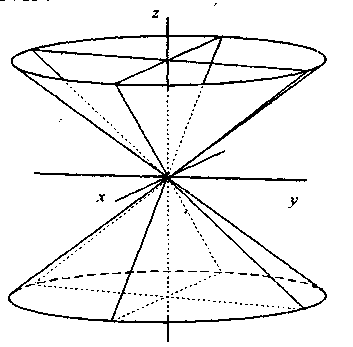
Рис. 11.5
Эта геометрическая особенность вытекает из того, что уравнение однородно, т.е. все его члены имеют одну и туже степень, равную 2. Иначе говоря, поверхность, определяемая однородным уравнением, состоит из прямых проходящих через начало координат. Такая поверхность называется конической или просто конусом. Прямые, из которых составлен конус, называются образующими. Точка, через которую они все проходят, называется вершиной конуса.
Рассмотрим сечение плоскостыс 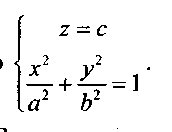
Плоскости z = h в сечении тоже дают эллипс. Это эллипс с полуосями a и b расположенный симметрично относительно координатных плоскостей Oxz и Oyz.
Если а =b, то эллипс превращается в окружность и конус называется круглым.
Нецентральные поверхности второго порядка
1°. Эллиптический параболоид.Каноническое уравнение имеет вид: 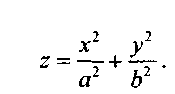
Плоскости Oxz и Oyz являются для него плоскостями симметрии. Ось Oz называется осью эллиптического параболоида. Из уравнения следует, что эллиптический параболоид расположен в полупространстве z 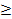 О. Линии пересечения представляют собой эллипсы
О. Линии пересечения представляют собой эллипсы
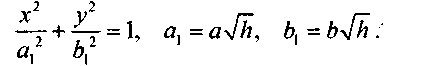
При увеличении h эллипсы бесконечно увеличиваются, так что эллиптический параболоид представляет собой бесконечную чашу. Плоскость х = h пересекает эллиптический параболоид по
параболе 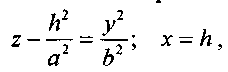 которая получается таким параллельным переносом параболы
которая получается таким параллельным переносом параболы 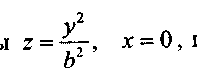 при котором ее вершина O(0,0,0) переходит в точку (h,0,z=h2/a2).
при котором ее вершина O(0,0,0) переходит в точку (h,0,z=h2/a2).
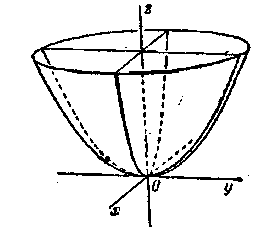
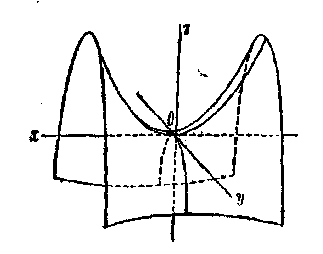
Рис. 11.6 Рис. 11.7
2°. Гиперболический параболоид. Каноническое уравнение имеет вид: 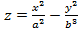 . Плоскости Oxz и Oyz являются плоскостями симметрии. Ось Oz называется осью гиперболического параболоида. Он имеет форму седла. Точка О называется вершиной гиперболического параболоида.
. Плоскости Oxz и Oyz являются плоскостями симметрии. Ось Oz называется осью гиперболического параболоида. Он имеет форму седла. Точка О называется вершиной гиперболического параболоида.
Линии пересечения гиперболического параболоида с плоскостями z = h при h > О представляют собой гиперболы:
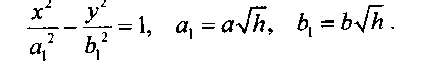
При h < О - линии пересечения сопряженных гипербол. Плоскость z = 0 пересекает гиперболический параболоид по двум прямым ( асимптотам гипербол) 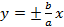 ,
, 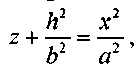
плоскость y= h пересекает гиперболический параболоид по параболе,
которая получается параллельным переносом параболы.
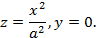
Цилиндры второго порядка
Рассмотрим цилиндрическую поверхность с образующей параллельной оси Oz.
В зависимости от характера сечения рассматриваемого цилиндра с плоскостью Оку различают цилиндры следующих типов:
1. Эллиптический цилиндр-каноническое уравнение:
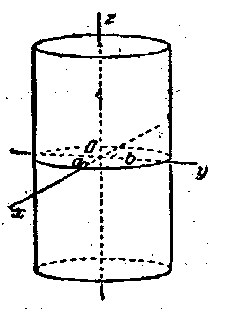
|
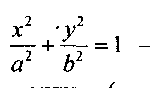
Направляющей является эллипс (рис.11.8).
Рис. 11.8
Если а =b, то цилиндр называется круговым.
2.Параболический цилиндр (рис.11.9). Направяющей является парабола.
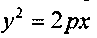
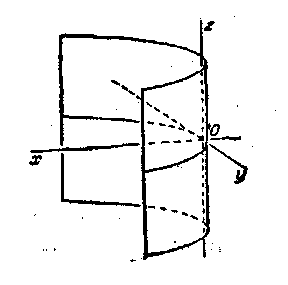
Рис. 11.9
3.Гиперболический цилиндр (рис.11.10). Направляющей является гипербола
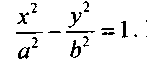
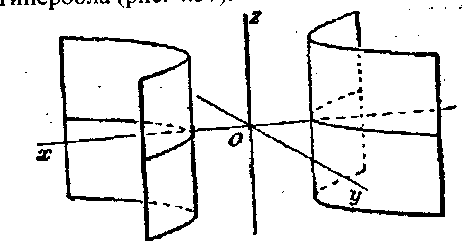
Рис. 11.10
Пример. Методом сечений исследовать форму и построить поверхность, заданную уравнением 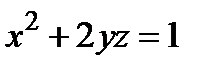 .
.
Решение.
1) В сечении поверхности плоскостью 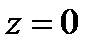 имеем две параллельные прямые
имеем две параллельные прямые 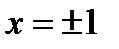 .
.
2) В сечении поверхности плоскостями 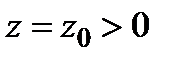 имеем семейство парабол
имеем семейство парабол 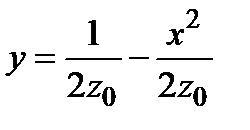 , вершины которых приближаются к оси
, вершины которых приближаются к оси  при увеличении
при увеличении 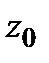 .
.
3) В сечении поверхности плоскостями 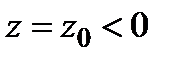 имеем семейство парабол
имеем семейство парабол 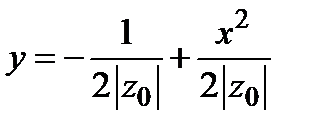 , вершины которых при-ближаются к оси
, вершины которых при-ближаются к оси 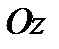 при увеличении
при увеличении 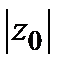 .
.
4) В сечении поверхности плоскостью 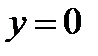 имеем две параллельные прямые
имеем две параллельные прямые 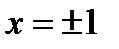
5) В сечении поверхности плоскостями y=y0>0 имеем семейство парабол 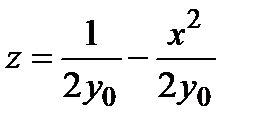 , вершины которых приближаются к оси
, вершины которых приближаются к оси 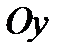 при увеличении
при увеличении 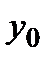 .
.
6) В сечении поверхности плоскостями 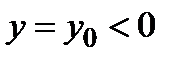 имеем семейство парабол
имеем семейство парабол 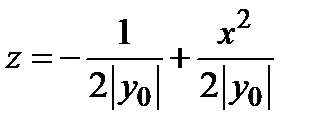 , вершины которых приближаются к оси
, вершины которых приближаются к оси  при увеличении
при увеличении  .
.
7) В сечении поверхности плоскостями 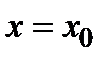 имеем семейство гипербол
имеем семейство гипербол 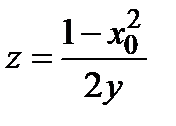 при
при 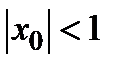 и
и 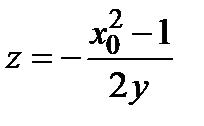 при
при 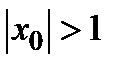 (сопряженные гиперболы). В случае
(сопряженные гиперболы). В случае 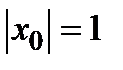 получается
получается 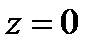 . Замечаем симметричность сечений поверхности относительно прямой
. Замечаем симметричность сечений поверхности относительно прямой 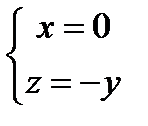 . Поэтому дальнейшее исследование проводим с учетом этого обстоятельства.
. Поэтому дальнейшее исследование проводим с учетом этого обстоятельства.

Рис. 11.11
8) В сечении поверхности плоскостями 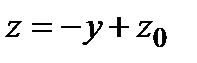 имеем семейство гипербол
имеем семейство гипербол 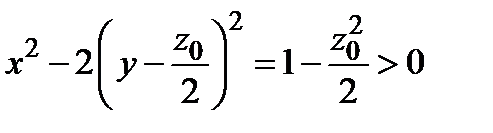 при
при 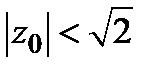 и
и 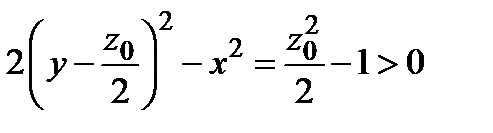 при
при 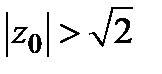 (сопряженные гиперболы). В случае
(сопряженные гиперболы). В случае 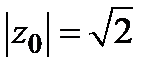 получаем две пересекающиеся прямые
получаем две пересекающиеся прямые 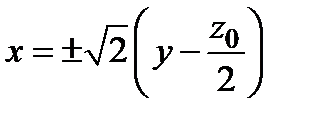 .
.
9) Сечения поверхности плоскостями 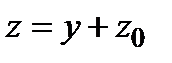 имеют проекции на плоскость
имеют проекции на плоскость 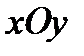 , описываемые уравнениями
, описываемые уравнениями 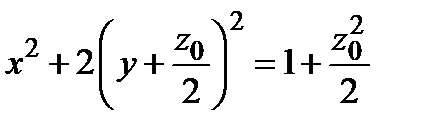 , т.е. эллипсы, у которых полуоси увеличиваются с увеличением
, т.е. эллипсы, у которых полуоси увеличиваются с увеличением 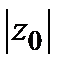 . Отношение полуосей этих эллипсов равно
. Отношение полуосей этих эллипсов равно 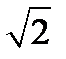 , а плоскости
, а плоскости 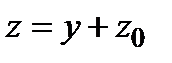 составляют угол 45º с плоскостью
составляют угол 45º с плоскостью 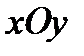 , поэтому сами сечения имеют форму окружностей.
, поэтому сами сечения имеют форму окружностей.
Выполненное исследование позволяет теперь достаточно детально изобразить заданную поверхность (рис. 11.11). Этой поверхностью является однополостный гиперболоид, ось которого – прямая 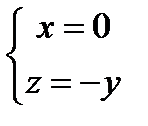 .
.
КОМПЛЕКСНЫЕ ЧИСЛА. ТЕОРЕМА
БЕЗУ. ЧИСЛОВАЯ ПОСЛЕДОВАТЕЛЬНОСТЬ
И ЕЕ ПРЕДЕЛ.
Комплексные числа и действия с ними
Алгебраическая форма z=a+b·i, b ?R, i2= - 1, гдеa = Re z – действительная часть числа (вещественная), b = i m – мнимачасть числа z. Если a ≠ 0, b≠ 0, то z - мнимое число (z = 97-7· i).
Если a = 0, b ≠ 0, то z - чисто мнимое число (z=55· i).
Если a≠0, b=0,то z - действительное число (z=-4).
Для i выполнено: i1 = i=> i4п+1 = i, i2= -1=> i4п+2= -1,i3= i2·
i=- i=> i4п+3=- i, i4=( i2)2=1 => i4п=1. Числа z=a+b·i и z=a-b·i– сопряженные; сумма и произведение двух сопряженных чисел являются действительными числами (z+ 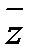 =2а, z·
=2а, z· 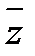 =а2+b2); z=a+b·i и -z=-a-b·i- противоположные. Сумма двух противоположных чисел равна 0(z+(- z)=0).
=а2+b2); z=a+b·i и -z=-a-b·i- противоположные. Сумма двух противоположных чисел равна 0(z+(- z)=0).
Для комплексных чисел, записанными в алгебраической форме справедливы все арифметические операции, как над обычными двучленами, учитывая лишь, что i2=-1
Условие равенства комплексных чисел z1=a1+b1·i и z2=a2+b2·i, z1= z2 , если a1 = a2 и b1 = b2 .
Сумма комплексных чисел z1=a1+b1·i и z2=a2+b2·i равна: z1+ z2=(a1+a2)+(b1+b2)·i.
Разность комплексных чисел: z1 - z2= (a1 - a2) + (b1 - b2) ·i
Произведение комплексных чисел равно: z1·z2 = (a1 · a2 – b1 · b2) + (a1 · a2 + b1 · b2).
Частное комплексных чисел равно:
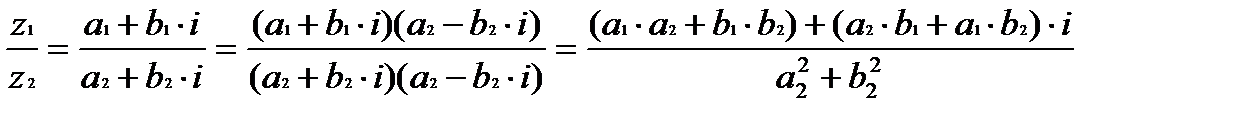
Понятие о комплексной плоскости.
Комплексная плоскость С – плоскость с прямоугольной декартовой системой координат x, y, каждая точка которой
(x; y) отождествлена с комплексным числом z=x+yi. Поэтому на комплексной плоскости говорят о точках z или о векторах z, подразумевается вектор, приложенный в начале координат с концом в точке z. Ось абсцисс OX на комплексной плоскости называется действительной осью, а ось ординат OY – мнимой осью.
Геометрическая форма комплексного числа.
Комплексное число c=a+b·i изображается на плоскости с декартовыми прямоугольными координатами точкой, имеющей координаты (a; b). Эта точка обозначается той же буквой z. Действительные числа изображаются точками оси абсцисс, а чисто – мнимые –точками оси ординат.
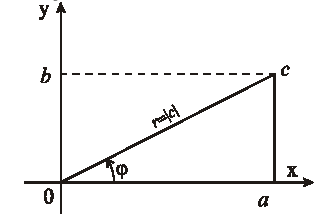
Рис. 12.1
Тригонометрическая форма комплексного числа.
z = r · (cos 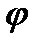 + i sin
+ i sin 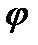 ), где r·cos
), где r·cos 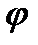 =Re z; r·sin
=Re z; r·sin 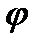 =Im z;
=Im z;
r = 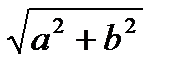 , cos
, cos 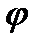 =
= 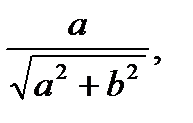 sin
sin 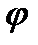 =
= 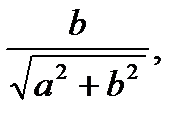
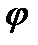 =Argz – главный аргумент комплексного числа z,-
=Argz – главный аргумент комплексного числа z,- 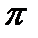 <
< 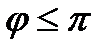 .
.
Для комплексных чисел z1=r1·(cosφ1+i·sinφ1) и z2=r2·(cosφ2+i·sinφ2) справедливы равенства:
z1·z2=r1·r2· (cos (φ1+ φ2) +i· sin (φ1+φ2));
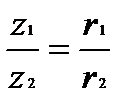 (cos (φ1- φ2) +i· sin (φ1-φ2)).
(cos (φ1- φ2) +i· sin (φ1-φ2)).
Для п-ой степени числа z справедливо равенство:
zn = rn(cos(nφ) + i·sin(nφ)), n 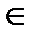 N.
N.
При r=1 эта формула называется формулой Муавра:
(cosφ + i· sinφ)n=cos(nφ)+i·sin(nφ).
Корень п-ой степени:
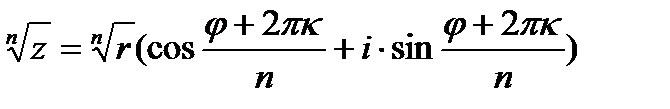 , где κ = 0, 1, 2, …, n-1
, где κ = 0, 1, 2, …, n-1
Показательная форма комплексного числа.
z=r·ei·φ. e±i·φ=cos φ±i ·sin φ – формула Эйлера.
Для комплексных чисел 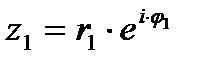 ,
, 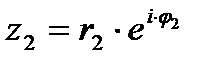 справедливы равенства:
справедливы равенства:
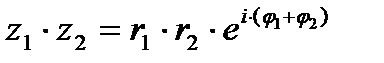 ;
; 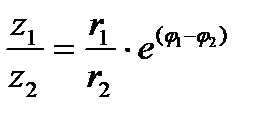 , где r2>0.
, где r2>0.
Для n-ой степени числа z справедливо равенство: zn=rn·ei·n·φ.
Корень n–ой степени из числа равен:
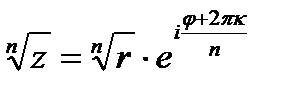 , κ=0,1,2,…,n-1
, κ=0,1,2,…,n-1
Пример . Найти все значения корня: 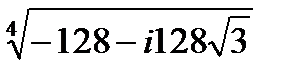
Решение: Корень n-й степени из комплексного числа z имеет n разных значений, которые находятся по формуле:
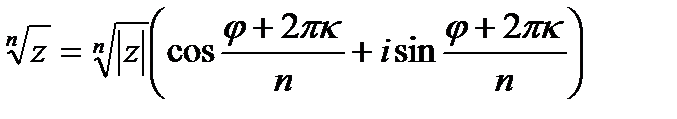
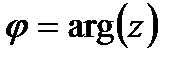 ; k=0, 1 ,…, n-1; z
; k=0, 1 ,…, n-1; z  0
0
Подставляя в эту формулу различные значения k, найдем все значения корня 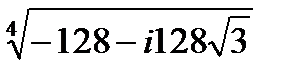 :
:
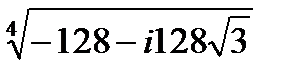 =
= 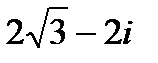 ,
, 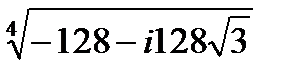 =
= 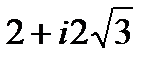
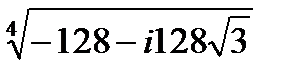 = -
= - 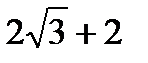 i,
i, 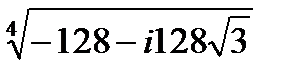 = -2 – i2
= -2 – i2 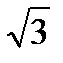
Ответ: 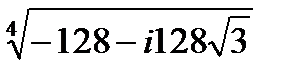 =
= 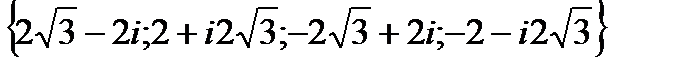
Теорема Безу.
Теорема Безу. Основная теорема алгебры.
Многочленом п-й степени в комплексной области называется функция вида
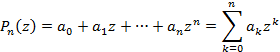
где ak,, k = 0,1,2,...,п - коэффициенты многочлена
( действительные или комплексные числа); z - комплексная переменная z = x + i y, x,y 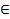 R.
R.
Если ak - действительные числа, многочлен называется многочленом в комплексной области с действительными коэффициентами. Область определения многочлена все комплексные числа, т.е. множество С. Любому числу z0 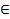 C соответствует число Pn (z0). Если Pn(z0)=0, то z0 называется корнем или нулеммногочлена Pn(z). Два многочлена называются равными
C соответствует число Pn (z0). Если Pn(z0)=0, то z0 называется корнем или нулеммногочлена Pn(z). Два многочлена называются равными 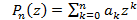 и
и 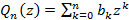 , если выполняется равенство ak = bk , к = 1,2,3,...,n.
, если выполняется равенство ak = bk , к = 1,2,3,...,n.
Теорема 1 (Безу). Для того, чтобы многочлен Pn(z) имел комплексный корень z0, необходимо и достаточно, чтобы он делился на двучлен z-z0, т.е. чтобы справедливым было представление Pn(z) = (z-z0) Pn (z) , где Pn-1(z) - многочлен степени п-1.
Необходимость. Пусть z0 корень многочлена Pn(z), тогда Pn(z0)=0. По формуле Тейлора для многочлена
Pn(z) = (z-z0) Pn (z)
Достаточность Если для многочлена справедливо представление в виде: Pn(z) = (z-z0) Pn (z) , то при z = z0 многочлен Pn(z0)=0, а это означает, что z0 -корень уравнения.
Из теоремы Безу не следует существование корней. Вопрос о существовании корней многочлена решает следующая теорема .
Теорема 2 (основная теорема алгебры).Любой многочлен Pn(z), n 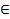 N, имеет по крайней мере один комплексный корень. Число z0 называется простым корнем многочлена Pn(z), если этот многочлен делится на (z -z0) и не делится на (z - z0)2 . Число z0 называется k- кратным корнем многочлена Pn(z), если Pn(z) делится на (z-z0)k и не делится (z-z0) k+1,т.е. Pn(z) представим в виде: Pn(z) = (z-z0)k Pn - k (z), где
N, имеет по крайней мере один комплексный корень. Число z0 называется простым корнем многочлена Pn(z), если этот многочлен делится на (z -z0) и не делится на (z - z0)2 . Число z0 называется k- кратным корнем многочлена Pn(z), если Pn(z) делится на (z-z0)k и не делится (z-z0) k+1,т.е. Pn(z) представим в виде: Pn(z) = (z-z0)k Pn - k (z), где
Pn -k (z) не делится на (z-z0).
Пример1.Показать, что z1 =0, z2 = -1 являются корнями многочлена P3(z) - z3 + 2z2 +z, и определить их кратность. При z1=0 многочлен P3 (z1) = 0. Разделим P3 (z) на z, получим P2(z) = z2 +2z + l, причем Р2 (z1) 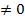 . Следовательно z1 = 0 является простым (однократным) корнем многочлена P3(z) = z3+2z2+z. При z2 = -1 Р3 (z2) = -1 + 2 -1 = 0. Представим Р3 (z) = z(z2 + 2z +1) = z(z +1)2. Отсюда делаем вывод, что z2 = -1 является корнем кратности два для многочлена P3(z) = z3+2z2+z.
. Следовательно z1 = 0 является простым (однократным) корнем многочлена P3(z) = z3+2z2+z. При z2 = -1 Р3 (z2) = -1 + 2 -1 = 0. Представим Р3 (z) = z(z2 + 2z +1) = z(z +1)2. Отсюда делаем вывод, что z2 = -1 является корнем кратности два для многочлена P3(z) = z3+2z2+z.
Следствие. Многочлен Pn(z) имеет п комплексных корней с учетом их кратности, т.е.
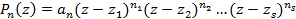 ,
,
где zl,, z2 , z3,... ,zs - различные корни Pn(z), a nl, n2,... ,ns - их кратности, причем n1+ n2+...+ns = п.
Многочлен с действительными коэффициентами. Разложение его на линейные и квадратные множители.
Рассмотрим многочлен n – й степени
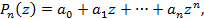 где ak
где ak 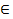 R,
R,
k = 0,1,2,...,n; z 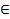 С.
С.
Для такого многочлена справедливы следующие две теоремы.
Теорема 3.Если многочлен Pn(z) с действительными коэффициентами, то
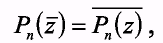
т.е. если Рп (z) = А + i B, А,В 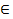 R, то Рп(
R, то Рп( 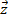 ) = A- i B.
) = A- i B.
Для комплексных чисел справедливы следующие равенства
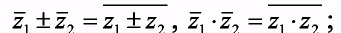
(доказываются непосредственной проверкой). Для действительных чисел 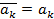 . Следовательно,
. Следовательно,
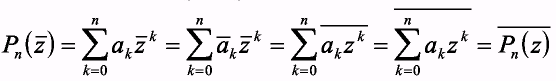
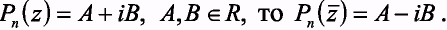
Теорема 4. Если многочлен Pn (z) с действительными коэффициентами имеет комплексный корень z0 = a + i b, то он имеет и сопряженный корень 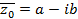 . Пусть z0 = a + i b - корень многочлена Pn(z). Тогда Pn (z0) = A + i B=0; А, В
. Пусть z0 = a + i b - корень многочлена Pn(z). Тогда Pn (z0) = A + i B=0; А, В 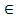 R. Комплексное число равно нулю, если равны нулю его действительная и мнимые части, А =0, В =0.
R. Комплексное число равно нулю, если равны нулю его действительная и мнимые части, А =0, В =0.
Вычислим
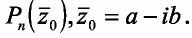
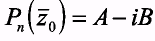
Имеем , учитывая, что А =0, В = 0, 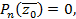
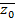 корень многочлена Pn (z). Из теоремы 4 следует, что если многочлен с действительными коэффициентами Pn(z) имеет комплексные корни, то они входят в его разложение попарно сопряженными.
корень многочлена Pn (z). Из теоремы 4 следует, что если многочлен с действительными коэффициентами Pn(z) имеет комплексные корни, то они входят в его разложение попарно сопряженными.
Рассмотрим произведение линейных множителей для попарно сопряженных
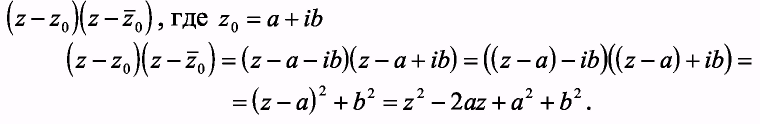
|
Обозначим a2+b2=q, -2a=p, тогда (z-a-ib)(z-a+ib) =z2+pz+q, т.е. получили квадратный трехчлен с действительными коэффициентами. Если число z0 = а + i b является корнем кратности k многочлена Pn(z] с действительными коэффициентами, то 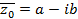 является многочленом той же кратности. Из всего сказанного следует, что многочлен с действительными коэффициентами Pn(z) разложим на множители с действительными коэффициентами первой и второй степени соответствующей кратности :
является многочленом той же кратности. Из всего сказанного следует, что многочлен с действительными коэффициентами Pn(z) разложим на множители с действительными коэффициентами первой и второй степени соответствующей кратности :
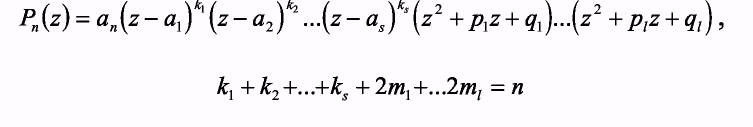
Пример2. Разложить на множители следующие многочлены:
1) Р3 (х) = х3-6х2 +11x-6
Найдем подбором один корень среди делителей 6. Это х=1. Остальные два можно найти, решая квадратное уравнение х2 +5х + 6=0, левая часть которого получается после деления многочлена Р3(х) = х3-6х2 +11x- 6 на х - l. Таким образом получаем еще два корня х2=2, х3=3. Тогда получим воспользовавшись формулами сокращенного умножения

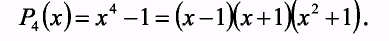
Числовая последовательность и ее предел.
В простейших случаях нахождение предела сводится к подстановке в данное выражение предельного значения аргумента. Часто, однако, приходится, прежде чем перейти к пределу, проводить тождественные преобразования данного выражения, как говорят, раскрывать неопределенность.
Неопределенности бывают нескольких видов: 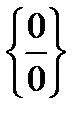 ,
, 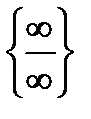 ,{
,{ 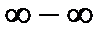 },{
},{ 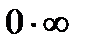 },{
},{ 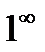 },{
},{ 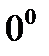 },{
},{ 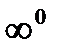 },{
},{ 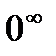 }. В последующих заданиях рассмотрим основные приемы, которыми обычно пользуются при таких преобразованиях для вычисления заданного предела. Функция f(x) называется функцией натурального аргумента, если множество значений x , для которых она определена, является множеством всех натуральных чисел: 1,2,3,..n. Например, f(n)=1+2+…+n=(n+1)n/2 - сумма n первых членов арифметической прогрессии.
}. В последующих заданиях рассмотрим основные приемы, которыми обычно пользуются при таких преобразованиях для вычисления заданного предела. Функция f(x) называется функцией натурального аргумента, если множество значений x , для которых она определена, является множеством всех натуральных чисел: 1,2,3,..n. Например, f(n)=1+2+…+n=(n+1)n/2 - сумма n первых членов арифметической прогрессии.
Числовой последовательностью называется бесконечное множество чисел a1,a2,…an, следующих одно за другим в определенном порядке и построенных по определенному закону, по которому общий членan последовательности задается как функция натурального аргумента, т.е. f(n)= an ( индекс n обозначает номер переменной величины an , т.е. n –го члена последовательности). Число А называется пределом последовательности an ,если для любого сколь угодно малого числа 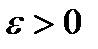 можно указать такой номер N , зависящий от
можно указать такой номер N , зависящий от 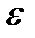 , что для всех номеров n>N выполняется неравенство:
, что для всех номеров n>N выполняется неравенство: 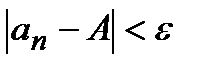 .
.
Пишут: 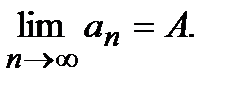 ,или
,или 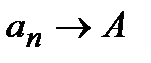 при
при 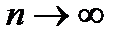 , если для
, если для 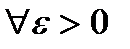
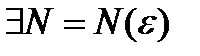 , что при
, что при 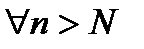 :
: 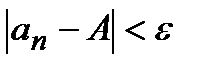 .
.
Числовая последовательность не может иметь более одного предела. Последовательность {an}, имеющая предел, называется сходящейся. В противном случае {an} будет расходящейся.
Пример 1.Вычислить 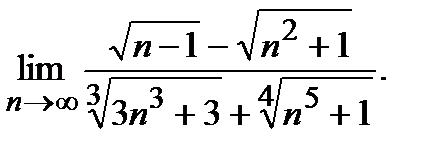
Решение.Выносим за скобки n в набольшей степени, т.е.
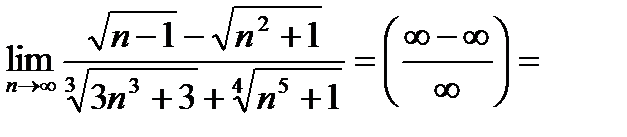
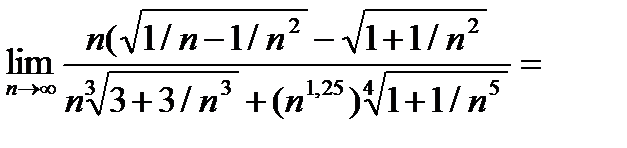
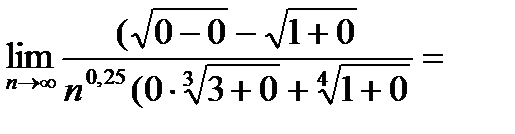
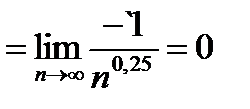
Число е и его применение.
Числом е называют предел
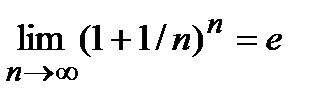 или
или
Дата: 2016-10-02, просмотров: 287.