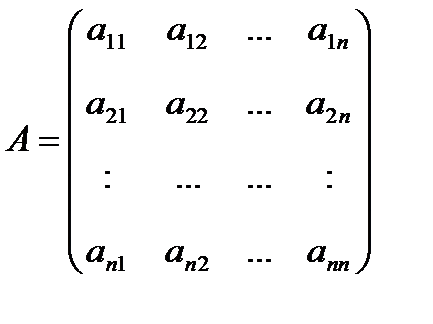
Пусть Rn - заданное n-мерное линейное пространство.
Ненулевой вектор 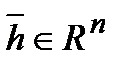 называется собственным вектором линейного оператора (преобразования) ,заданного матрицей А , если найдется такое число
называется собственным вектором линейного оператора (преобразования) ,заданного матрицей А , если найдется такое число 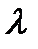 , что выполняется равенство
, что выполняется равенство 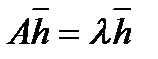 . Само число
. Само число 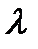 называют собственным (или характеристическим) числом оператора А, соответствующим собственному вектору
называют собственным (или характеристическим) числом оператора А, соответствующим собственному вектору 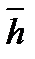 . Собственные (значения) матрицы А являются корнями характеристического уравнения det (A-
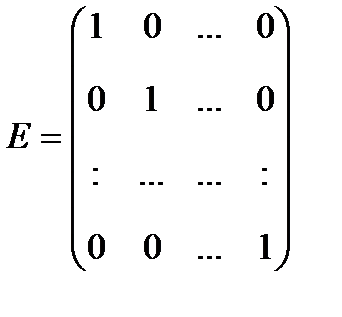
. Собственные (значения) матрицы А являются корнями характеристического уравнения det (A- 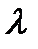 E)=0, являющегося алгебраическим уравнением n-ой степени. Если
E)=0, являющегося алгебраическим уравнением n-ой степени. Если
 ,
, , то характеристическое уравнение в координатной форме имеет вид:
, то характеристическое уравнение в координатной форме имеет вид:
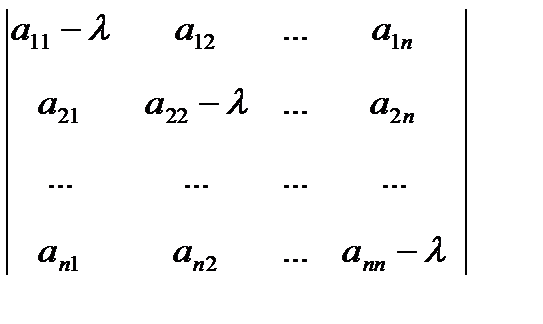 =0 (***)
=0 (***)
Для нахождения ненулевого собственного вектора
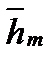 =
= 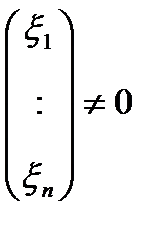 , отвечающему собственному числу
, отвечающему собственному числу 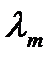 ,
,
m=1,2,…n надо решить линейную однородную систему (ЛОС) уравнений: 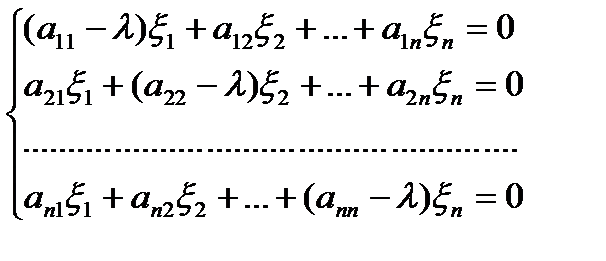
Эта ЛОС уравнений имеет бесконечно много решений. Поэтому, собственному значению 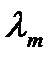 соответствует семейство собственных векторов. Выбирают любой из них.
соответствует семейство собственных векторов. Выбирают любой из них.
Если характеристическое уравнение (***) имеет n различных корней, то соответствующие им собственные векторы 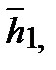
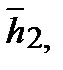 …
… 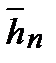 - линейно независимые и образуют базис. Если среди корней характеристического уравнения (*) имеются кратные, т.е. равные корни, например,
- линейно независимые и образуют базис. Если среди корней характеристического уравнения (*) имеются кратные, т.е. равные корни, например, 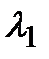 - корень кратности к, то хорошо найти к линейно независимых собственных векторов
- корень кратности к, то хорошо найти к линейно независимых собственных векторов 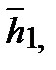
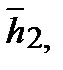 …
… 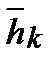 , отвечающих собственному значению, кратности к; их число m=n-r , где n-порядок матрицы(A-
, отвечающих собственному значению, кратности к; их число m=n-r , где n-порядок матрицы(A- 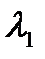 E), r=Rang (A-
E), r=Rang (A- 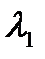 E);
E); 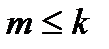 .
.
Пример.Найти собственные значения и собственные векторы матрицы А. Дано: 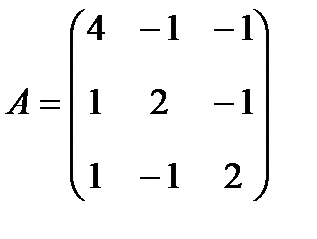 .
.
Решение. Решаем характеристическое уравнение
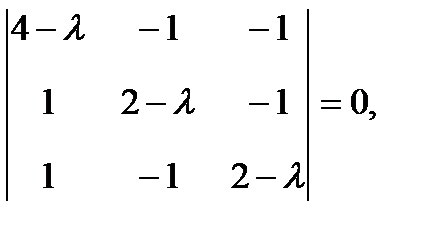
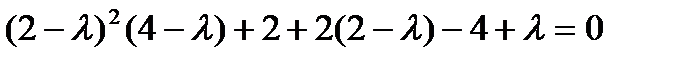
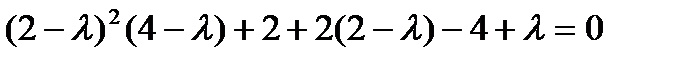 или
или 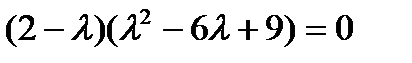 ,
, 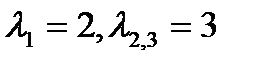 .
.
Откуда 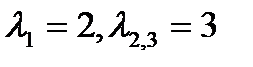 -собственные значения матрицы А.
-собственные значения матрицы А.
Для простого корня 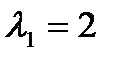 находим собственный вектор
находим собственный вектор 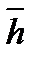 =
= 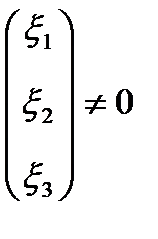 , решая ЛОС уравнений
, решая ЛОС уравнений 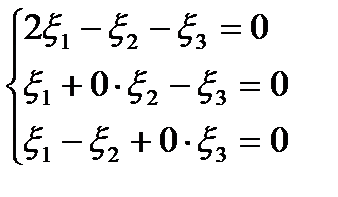
коэффициенты этой системы равны элементам определителя det (A- 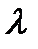 E)=0, при
E)=0, при 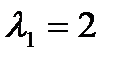 :
: 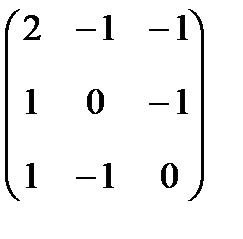
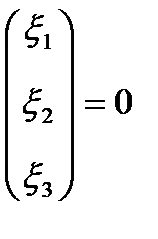 .
.
Решим методом Гаусса: 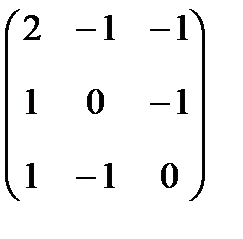
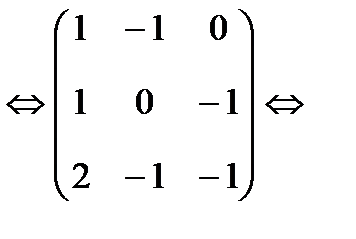
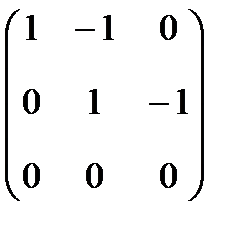 , получим
, получим 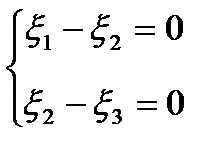 или
или 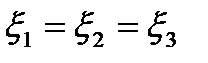 , где
, где 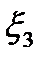 -свободная переменная , полагая
-свободная переменная , полагая 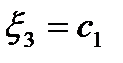 , получаем,
, получаем, 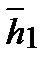 =
= 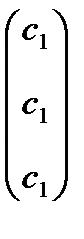 -семейство собственных векторов, отвечающих собственному значению
-семейство собственных векторов, отвечающих собственному значению 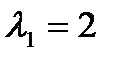 . Например,
. Например, 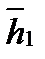 =
= 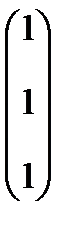 . Для кратного корня
. Для кратного корня 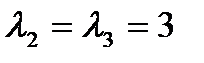 сначала определим число линейно независимых собственных векторов. Подставляя
сначала определим число линейно независимых собственных векторов. Подставляя 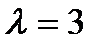 в левую часть характеристического уравнения, получаем матрицу
в левую часть характеристического уравнения, получаем матрицу 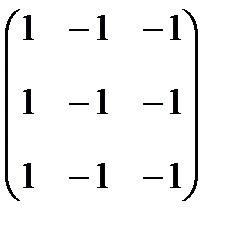 . Ее порядок n=3, ранг r=1 (наивысший порядок миноров, не равных нулю). Число линейно независимых собственных векторов равно m=n-r=2 совпадает с кратностью корня к=2. Найдем их. Имеем
. Ее порядок n=3, ранг r=1 (наивысший порядок миноров, не равных нулю). Число линейно независимых собственных векторов равно m=n-r=2 совпадает с кратностью корня к=2. Найдем их. Имеем 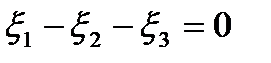 или
или 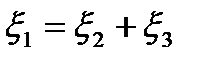 .Полагая
.Полагая 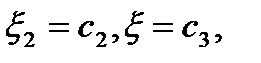 где
где 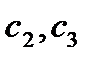 -любые константы, одновременно не обращающееся в ноль, получим
-любые константы, одновременно не обращающееся в ноль, получим 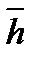 =
= 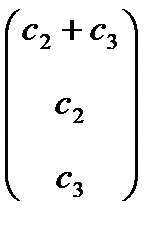 - семейство собственных векторов для
- семейство собственных векторов для 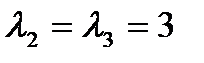 . Пусть
. Пусть 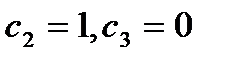 . Тогда
. Тогда 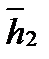 =
= 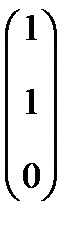 . Пусть
. Пусть 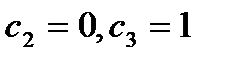 . Тогда
. Тогда 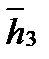 =
= 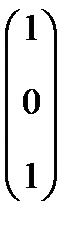 . Два линейно независимых собственных вектора
. Два линейно независимых собственных вектора 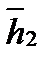 и
и 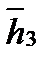 , соответствующих собственному числу
, соответствующих собственному числу 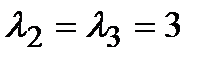 .
.
Ответ: 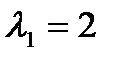 ,
, 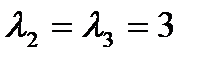 – собственные значения матрицы A,
– собственные значения матрицы A, 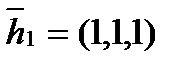 ,
, 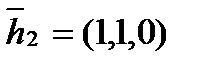 ,
,
Приведение квадратичной формы
К каноническому виду
Квадратичной формой действительных переменных
x1, x2,…,xn называется однородный многочлен второй степени относительно этих переменных, не содержащий свободного члена и членов первой степени. Если число переменных n=2 . то квадратичная форма: 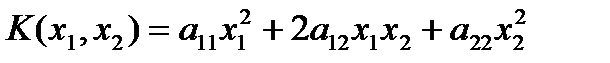 . Если n=3, то
. Если n=3, то 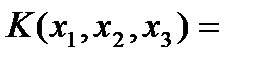
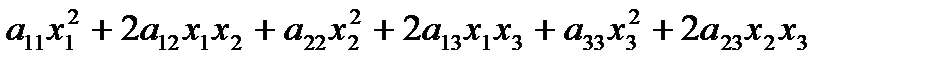 .
.
Приведение квадратичной формы к каноническому виду ортогональным преобразованием.
Рассмотрим квадратичную форму трех переменных 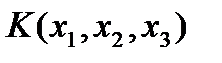 . Симметрическая матрица
. Симметрическая матрица
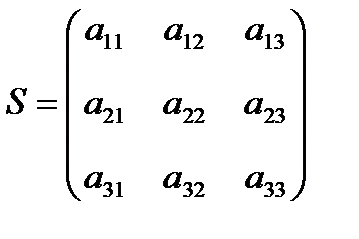 , у которой
, у которой 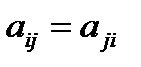 , (i,j =1,2,3 при
, (i,j =1,2,3 при 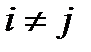 ) называется матрицей квадратичной формы
) называется матрицей квадратичной формы 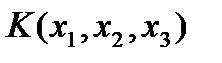 . Так как S - симметричная матрица, то корни
. Так как S - симметричная матрица, то корни 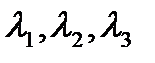 характеристического уравнения
характеристического уравнения
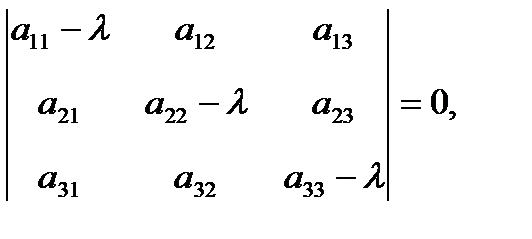
являются действительными числами и будут собственными значениями матрицы S . Известно, что собственные векторы симметрической матрицы, соответствующие различным собственным значениям, ортогональны. Следовательно, если матрица симметрическая, то можно говорить об ортогональном базисе векторов, составленном из собственных векторов этой матрицы. Если среди корней характеристического уравнения есть корень кратности к, то можно указать к линейно независимых векторов, отвечающих этому собственному значению, согласно следующей теореме.
Теорема. Для того чтобы существовал базис из собственных векторов матрицы оператора А, необходимо и достаточно, чтобы каждому собственному значению соответствовало столько линейно независимых собственных векторов, какова его кратность. Число линейно независимых векторов равно
m=n-r , где n -размерность матрицы, r=Rang S .
И так, каждому оператору в разных базисах соответствуют различные матрицы. Наша цель: найти такой базис, в котором матрица оператора имела бы простейший вид, а именно диагональный. В ортонормированном базисе из собственных векторов матрица оператора имеет диагональный вид:
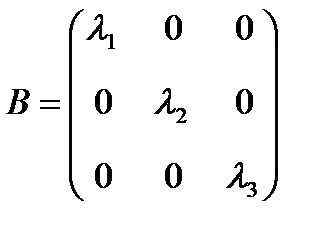 ,где на главной диагонали стоят
,где на главной диагонали стоят
собственные значения матрицы S , ибо характеристический многочлен линейного оператора (преобразования) не зависит от базиса. Известно, что квадратичную форму 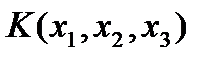 можно представить в виде скалярного произведения
можно представить в виде скалярного произведения
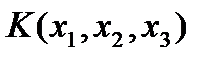 =
= 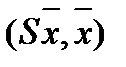 , где
, где
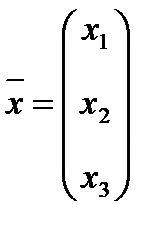 ,
, 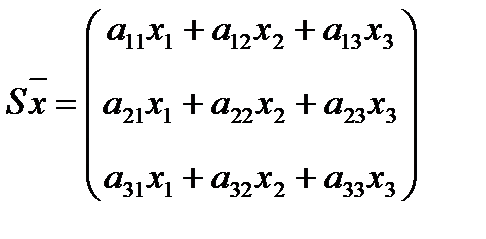 .
.
Переходя к новому ортонормированному базису, где матрица перехода B=T-1ST , старые и новые переменные (координаты) связаны преобразованием 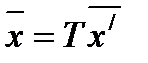 , где
, где 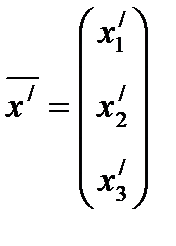 -вектор
-вектор 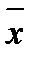 в новой системе координат, получим квадратичную форму в новой системе координат, определенной базис из собственных нормированных векторов, в виде
в новой системе координат, получим квадратичную форму в новой системе координат, определенной базис из собственных нормированных векторов, в виде
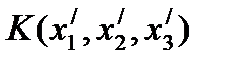 =
= 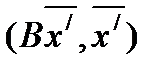 =
= 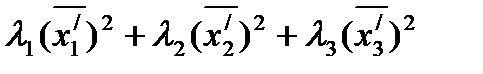 ,
,
не содержащем членов с произведением переменных,  , который называется каноническим видом.
, который называется каноническим видом.
Формулы преобразования координат при переходе к новому ортонормированному базису имеют вид:
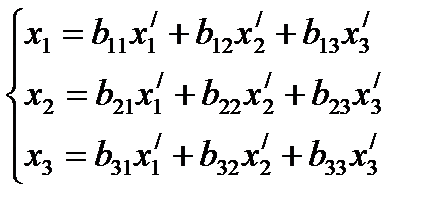 , где нормированные собственные векторы матрицы S:
, где нормированные собственные векторы матрицы S: 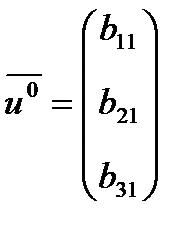 ,
, 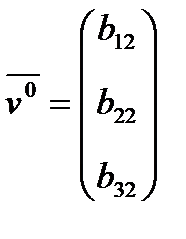 ,
, 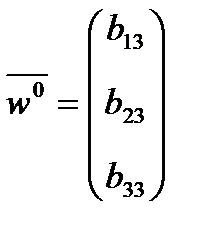 принято говорить, что квадратичная форма
принято говорить, что квадратичная форма 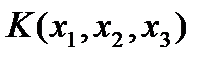 приведена к каноническому виду с помощью ортогонального преобразования.
приведена к каноническому виду с помощью ортогонального преобразования.
Вывод. Чтобы привести каноническую форму к каноническому виду надо:
1) По коэффициентам квадратичной формы составить симметрическую матрицу S;
2) Найти собственные значения и собственные векторы матрицы S, причем собственные векторы пронормировать;
3) Записать квадратичную форму в каноническом виде
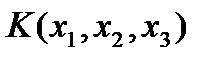 =
= 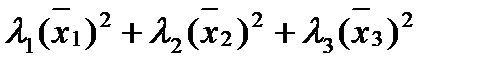 .
.
Векторы и действия над ними
Вектор – это направленный отрезок, т.е. имеющий длину и направление. Длина вектора называется модулем и обозначается  или
или 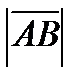 . Векторы
. Векторы 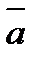 ,
, 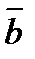 - коллинеарны (
- коллинеарны ( 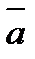 //
// 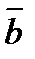 ) , если параллельны одной и той же прямой или лежат на одной прямой.
) , если параллельны одной и той же прямой или лежат на одной прямой.
Векторы 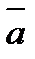 ,
, 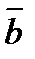 ,
, 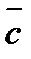 – компланарны, если они параллельны одной и той же плоскости или лежат в одной и той же плоскости.
– компланарны, если они параллельны одной и той же плоскости или лежат в одной и той же плоскости.
Направление вектора определяется углами α, β, γ, образованными вектором с положительным направлением координатных осей OX , OY , OZ соответственно.
Направляющие косинусы вектора вычисляются по формулам: 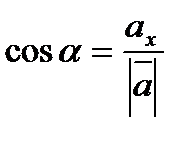 ,
, 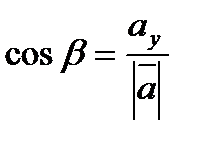 ,
, 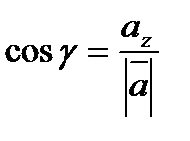 , где
, где 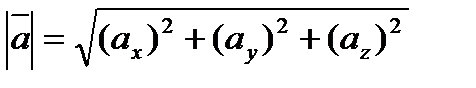 , если известны его координаты
, если известны его координаты 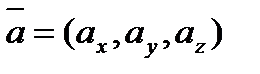 . Заметим, что направляющие косинусы являются координатами любого единичного вектора, т.е.
. Заметим, что направляющие косинусы являются координатами любого единичного вектора, т.е.
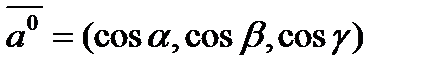 , если
, если 
Основные действия над векторами.
Пусть даны 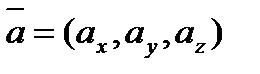 и
и 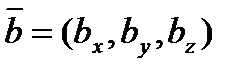 .
.
Тогда:
1. 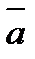
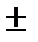
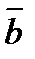 =
= 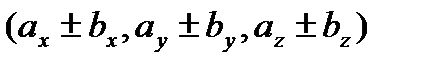
2. 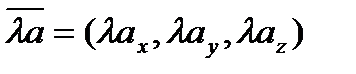 , где
, где 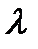 -действительное число.
-действительное число.
3. Скалярное произведение 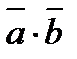 двух векторов
двух векторов 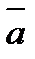 и
и 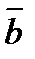 есть число, по определению равное
есть число, по определению равное 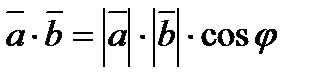 ,где
,где 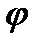 -угол между двумя векторами
-угол между двумя векторами 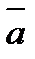 и
и 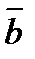 вычисляется по формуле:
вычисляется по формуле: 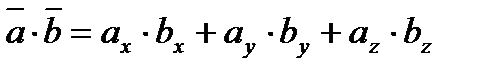 .
.
4. Векторное произведение 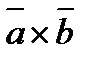 двух векторов
двух векторов 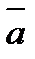 и
и 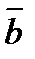 - есть вектор
- есть вектор 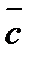 , удовлетворяющий трем условиям:
, удовлетворяющий трем условиям:
1) вектор 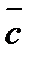 направлен так, что векторы
направлен так, что векторы 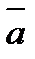 ,
, 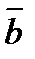 и
и 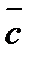 образуют правую тройку;
образуют правую тройку;
2) вектор 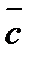 ортогонален вектора
ортогонален вектора 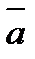 и
и 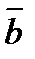 , т.е.
, т.е. 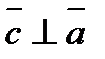 ,
, 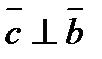 .
.
3) модуль 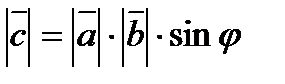 , де
, де 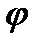 - угол между двумя векторами
- угол между двумя векторами 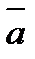 и
и 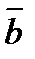 . Геометрически модуль векторного произведения равен площади параллелограмма, построенного на этих векторах, т.е.
. Геометрически модуль векторного произведения равен площади параллелограмма, построенного на этих векторах, т.е. 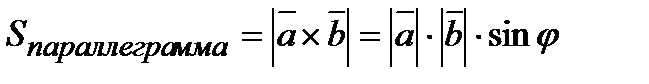 .
.
Тогда 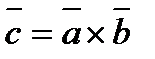 .
.
5. Смешанное произведение трех векторов 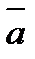 ,
, 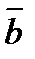 и
и 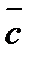 есть число равное по определению:
есть число равное по определению: 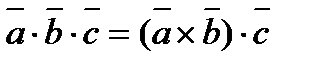 .
.
Геометрически модуль смешанного произведения равен объему параллепипеда, построенного на этих векторах, т.е. 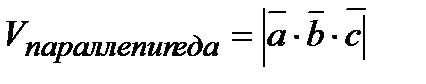 . Заметим, что объем тетраэдра, построенного на трех векторах
. Заметим, что объем тетраэдра, построенного на трех векторах 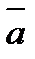 ,
, 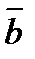 и
и 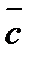 равен
равен 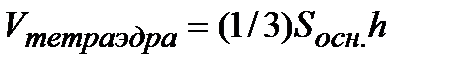 , где Sосн. – площадь основания тетраэдра, h –высота тетраэдра, т.к. основание тетраэдра есть треугольник, построенный на векторах
, где Sосн. – площадь основания тетраэдра, h –высота тетраэдра, т.к. основание тетраэдра есть треугольник, построенный на векторах 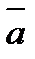 и
и 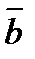 , то Sосн=(1/2) Sпараллелограмма, следовательно,
, то Sосн=(1/2) Sпараллелограмма, следовательно,
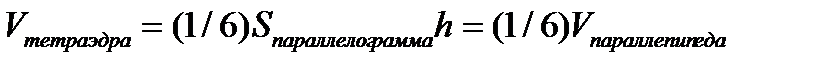 .
.
Если заданы векторы в координатах 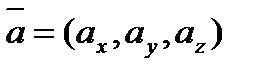 ,
, 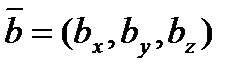 и
и 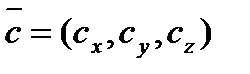 , то
, то
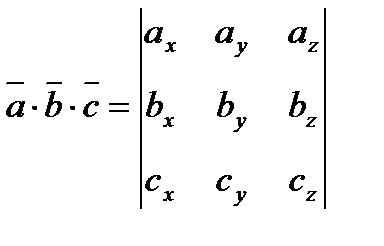 смешанное произведение.
смешанное произведение.
1) Условие перпендикулярности векторов ( 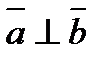 ):
): 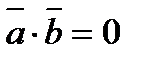
или 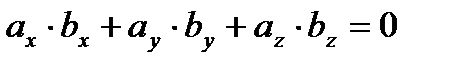 .
.
2) Условие коллинеарности векторов ( 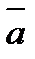 //
// 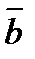 ):
):
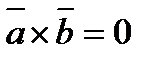 или
или 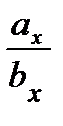 =
= 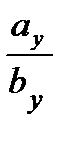 =
= 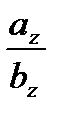 .
.
3) Условие компланарности векторов 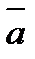 ,
, 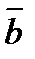 ,
, 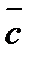 :
: 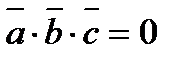 или
или
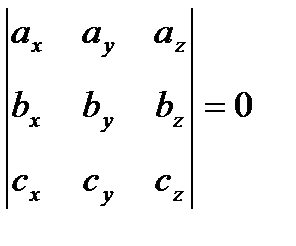
Пример.Вычислить объем тетраэдра с вершинами в точках А1, А2, А3, А4 и его высоту, опущенную из вершины А4 на грань А1 А2 А3(рис.2).
Дано: А1(-1;2;-3), А2(4;-1;0), А3(2;1;-2); А4(3;4;5).
Требуется найти объем тетраэдра.
Решение. а) Объем тетраэдра равен 1/6 части объема
параллелепипеда, построенного на векторах
 ,
,  ,
, 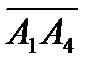 . Объем соответствующего параллелепипеда вычисляется через смешанное произведение векторов, совпадающих с ребрами тетраэдра, сходящимися в вершине А1(рис.7.1):
. Объем соответствующего параллелепипеда вычисляется через смешанное произведение векторов, совпадающих с ребрами тетраэдра, сходящимися в вершине А1(рис.7.1):
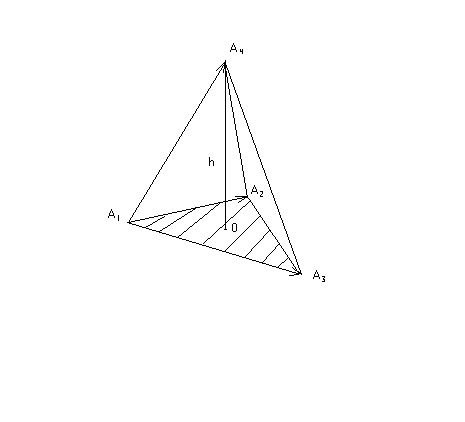
Рис. 7.1
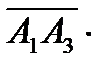
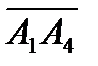
Найдем координаты векторов и их смешанное произведение: 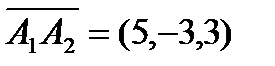 ,
, 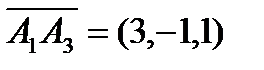 ,
, 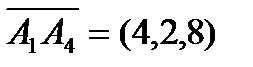
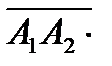
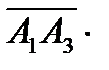
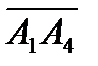 =
= 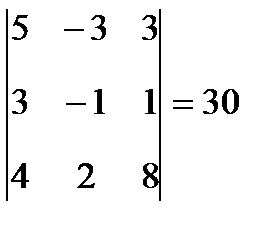
Откуда 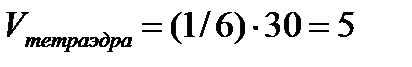 (куб. ед.)
(куб. ед.)
б) Искомую высоту h найдем из формулы: 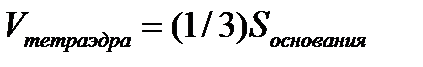 h , где Sоснования равна площади треугольника А1 А2 А3.
h , где Sоснования равна площади треугольника А1 А2 А3.
Площадь треугольника А1 А2 А3 равна половине площади параллелограмма, построенного на векторах 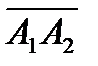 ,
, 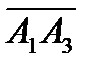
Поэтому находим векторное произведение

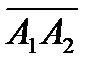
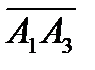 =
= 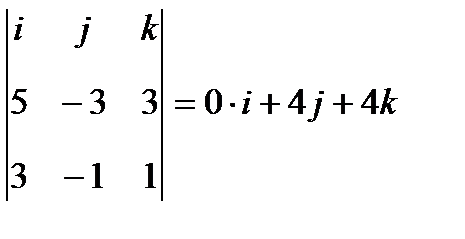
Следовательно, Sоснования= 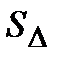 =
= 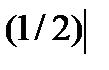
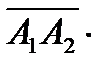
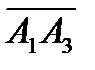
 =
=
= 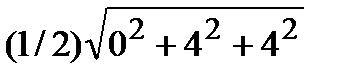 =2
=2 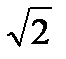 (кв.ед.)
(кв.ед.)
Таким образом
h=3Vтетраэдра/Sоснования=3.5/(2 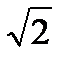 )=15
)=15 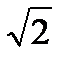 /4
/4
Ответ:Vтетраэдра=5 (куб. ед.), h=15 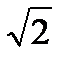 /4(ед. длины)
/4(ед. длины)
8. Плоскость и прямая в пространстве
Плоскость в пространстве.
1) Уравнение плоскости – это уравнение первой степени вида: Ax+By+Cz+D = 0, если А2+В2+С2 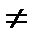 0, которое называется общим уравнением. Коэффициенты А, В ,С можно рассматривать, как координаты вектора нормали
0, которое называется общим уравнением. Коэффициенты А, В ,С можно рассматривать, как координаты вектора нормали 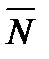 =(A,B,C), перпендикулярного плоскости.
=(A,B,C), перпендикулярного плоскости.
2) Уравнение плоскости, проходящей через точку
M0(x0, y0 , z0) перпендикулярно вектору 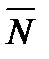 :
:
A(x-x0)+B(y-y0)+C(z-z0)=0, (условие 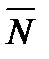
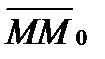 , где
, где
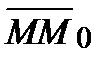 =(x-x0 , y-y0 , z-z0) лежит в плоскости).
=(x-x0 , y-y0 , z-z0) лежит в плоскости).
3) Уравнение плоскости, проходящей через три заданные точки M1(x1,y1,z1), M2(x2,y2 ,z2), M3(x3,y3,z3) имеет вид:
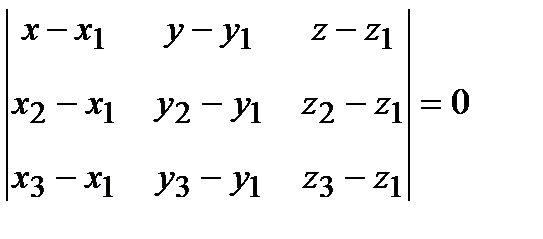
-условие компланарности векторов 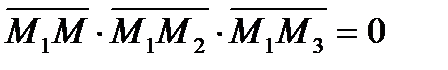 , где
, где 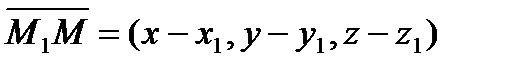 ,
, 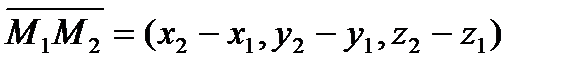 ,
, 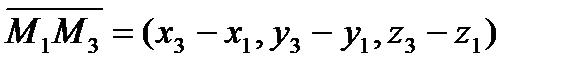 , где M(x,y,z)- текущая точка данной плоскости.
, где M(x,y,z)- текущая точка данной плоскости.
4) Уравнение плоскости в отрезках имеет вид:
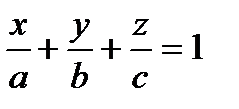 , где а,b,с – отрезки, отсекаемые плоскостью, на координатных осях соответственно, - абсцисса, ордината и аппликата точек пересечения плоскости с осями ox, oy, и oz.
, где а,b,с – отрезки, отсекаемые плоскостью, на координатных осях соответственно, - абсцисса, ордината и аппликата точек пересечения плоскости с осями ox, oy, и oz.
5) Нормальное уравнение плоскости:
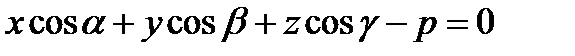 , где
, где 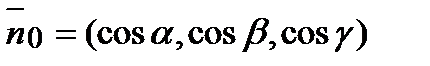 - вектор- нормаль к плоскости единичной длины, проведены из начала координат, p – расстояние от начала координат до плоскости (p>0).
- вектор- нормаль к плоскости единичной длины, проведены из начала координат, p – расстояние от начала координат до плоскости (p>0).
Приведем общее уравнение плоскости к нормальному уравнению плоскости. Для этого умножим обе части общего уравнения плоскости на нормирующей множитель:
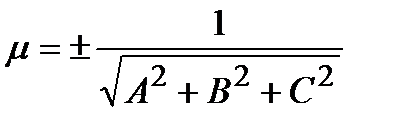 - полученное уравнение и будет нормальным уравнением плоскости. (Знак
- полученное уравнение и будет нормальным уравнением плоскости. (Знак 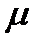 берется противоположным знаку D)
берется противоположным знаку D)
Расстояние от данной точки M0 (x0,y0,z0) до плоскости находится по формуле
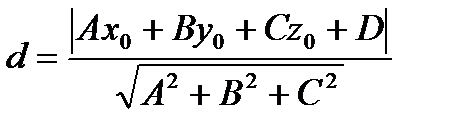
где A,B,C-коэффициенты в общем уравнении плоскости,
Угол между двумя плоскостями вычисляется по формуле:
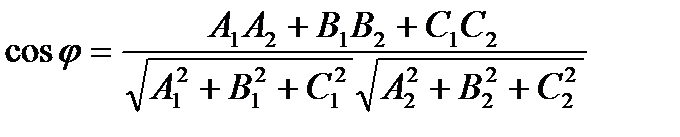 ,
,
где под углом между двумя плоскостями понимается угол между их нормалями  и
и  .
.
Условие перпендикулярности двух плоскостей:
A1 A2+B1 B2+C1C2=0 (если 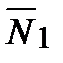
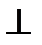
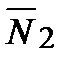 ).
).
Условие параллельности двух плоскостей:
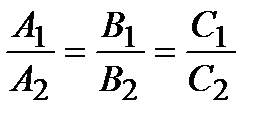 (если
(если 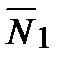 //
// 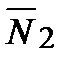 ).
).
Прямая в пространстве
Канонические уравнения прямой имеют вид
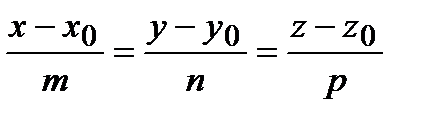 , где
, где 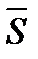 =(m,n,p) – направляющий вектор прямой, точка M(x0,0y.z0 ) лежит на прямой, т.е. прямая проходит через точку M0 параллельно вектору
=(m,n,p) – направляющий вектор прямой, точка M(x0,0y.z0 ) лежит на прямой, т.е. прямая проходит через точку M0 параллельно вектору 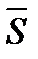 .
.
Уравнение прямой в параметрической форме:
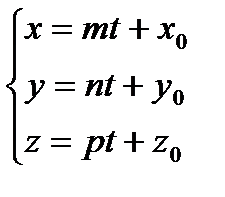
Прямая может быть задана как линия пересечения двух плоскостей 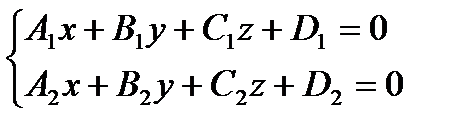
Уравнение прямой, проходящей через две точки M1(x1,y1,z1) и M2(x2,y2,z2 ) имеет вид: 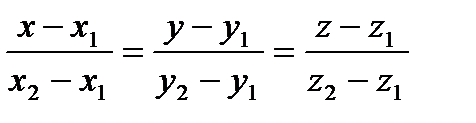 .
.
Угол между двумя прямыми вычисляются по формуле
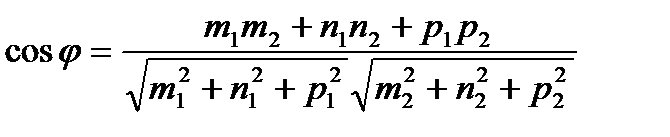 ,
,
где угол 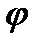 между двумя прямыми- угол между их направляющими векторами данных прямых.
между двумя прямыми- угол между их направляющими векторами данных прямых.
Условие перпендикулярности двух прямых:
m1 m2+n1 n2+p1p2=0 (если 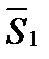
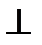
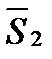 ).
).
Условие параллельности двух прямых:
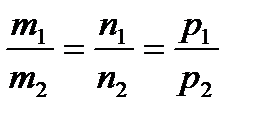 (если
(если 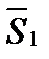 //
// 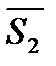 ).
).
Взаимное расположение прямой и плоскости
Пусть заданы прямая 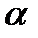 и плоскость
и плоскость 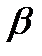 :
:
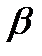 : Ax+By+Cz+D = 0,
: Ax+By+Cz+D = 0,
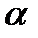 :
: 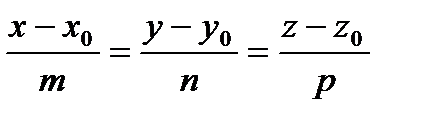
Угол между прямой и плоскостью определяются по
формуле
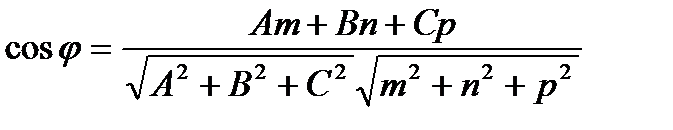 ,
,
где 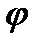 -угол между направляющим вектором прямой и нормалью к плоскости. Условие перпендикулярности прямой и плоскости:
-угол между направляющим вектором прямой и нормалью к плоскости. Условие перпендикулярности прямой и плоскости: 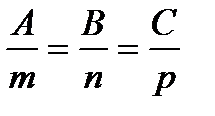 (если
(если 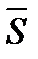 //
// 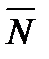 ). Условие параллельности двух прямых: A m+Bn+Cp=0 (если
). Условие параллельности двух прямых: A m+Bn+Cp=0 (если 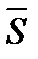
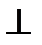
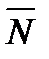 ). Напомним, что
). Напомним, что 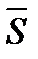 =(m,n,p ) – направляющий вектор прямой ,
=(m,n,p ) – направляющий вектор прямой , 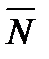 =(A,B,C) – нормаль к плоскости.
=(A,B,C) – нормаль к плоскости.
Пример. Найти расстояние d от точки M0 до плоскости, проходящей через три точки M1,M2,M3.
Дано: M1(1;0;2);M2(1;2;-1);M3 (2;-2;1);M0 (-5;-9;1).
Требуется найти: d (см. рис.8.1)
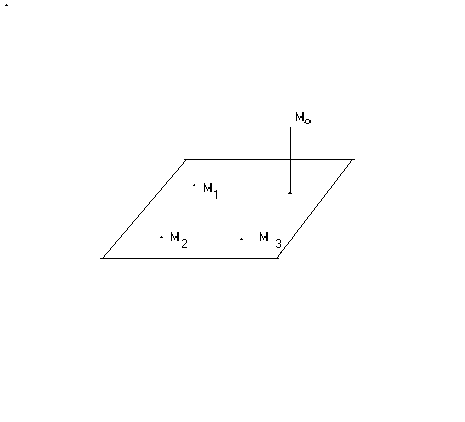
Рис.8.1
Решение. Находим уравнение плоскости, проходящей через три заданные точки M1, M2, M3, по формуле
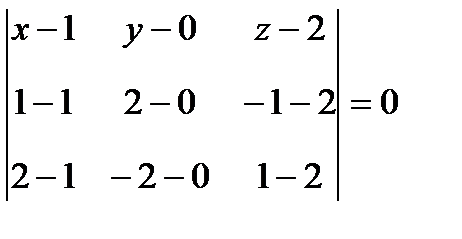
Разложив определитель по первой строке и, приводя подобные члены, имеем уравнение плоскости: 8x+3y+2z-12=0
Расстояние d от данной точки M0 (x0,y0,z0) до плоскости, определяемой уравнением Ax+By+Cz+D=0, находится по формуле
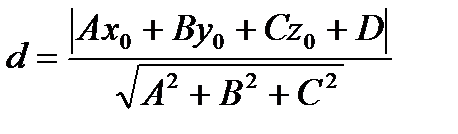 =
= 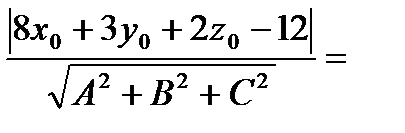
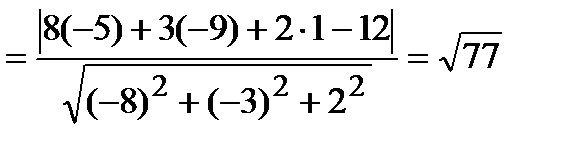 (ед. длины).
(ед. длины).
Кривые второго порядка
На плоскости
1.Окружность – это множество точек плоскости, равноудаленных от данной точки (центра). Если R – радиус окружности, точки M0 (x0,y0) - ее центр, то каноническое уравнение окружности имеет вид : (x-x0)2+(y-y0)2=R2 .
2. Эллипс – это множество точек плоскости, сумма расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная, равная 2а, причем эта постоянная больше расстояния между фокусами (рис.9.1).
Пусть 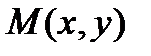 – любая точка эллипса,
– любая точка эллипса, 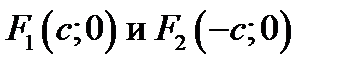 – фокусы. Тогда по определению имеем
– фокусы. Тогда по определению имеем 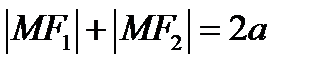 , где
, где 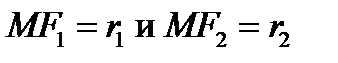 называются фокальными радиусами, и, следовательно,
называются фокальными радиусами, и, следовательно, 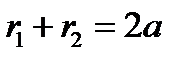 .
.
Рис. 9.1
Форма эллипса (мера его сжатия) характеризуется его эксцентриситетом 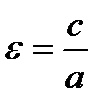 , (так как с < а, то e < 1 для эллипса). Каноническое уравнение эллипса :
, (так как с < а, то e < 1 для эллипса). Каноническое уравнение эллипса : 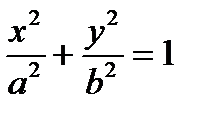 , причем
, причем 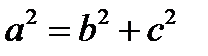 . Здесь a – большая,
. Здесь a – большая, 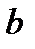 – малая полуоси эллипса. Если а =
– малая полуоси эллипса. Если а = 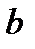 (с = 0, e = 0, фокусы сливаются в одной точке – центре), то эллипс превращается в окружность
(с = 0, e = 0, фокусы сливаются в одной точке – центре), то эллипс превращается в окружность 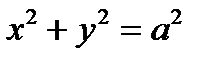 . Фокальные радиусы эллипса:
. Фокальные радиусы эллипса: 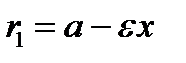 (правый фокальный радиус) и
(правый фокальный радиус) и 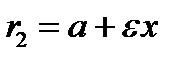 (левый фокальный радиус).
(левый фокальный радиус).
3.Гипербола – это множество точек плоскости, абсолютная величина разности расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная, равная 2а, причем эта постоянная меньше расстояния между фокусами (рис.9.2). Пусть
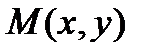 – любая точка гиперболы,
– любая точка гиперболы, 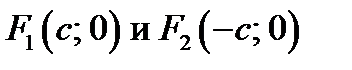 – фокусы. Тогда по определению имеем
– фокусы. Тогда по определению имеем
Рис. 9.2
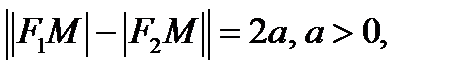 где
где 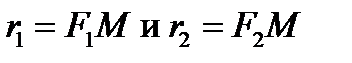 называются фокальными радиусами, причем для правой ветви гиперболы,
называются фокальными радиусами, причем для правой ветви гиперболы, 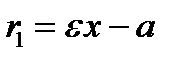 – правый фокальный радиус;
– правый фокальный радиус; 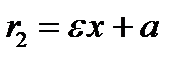 – левый фокальный радиус, где число
– левый фокальный радиус, где число 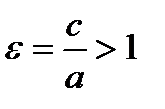 называется эксцентриситетом гиперболы. Каноническое уравнение гиперболы имеет вид
называется эксцентриситетом гиперболы. Каноническое уравнение гиперболы имеет вид 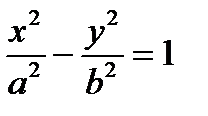 , где
, где
а2 + в2 = с2. Здесь а – действительная полуось, b – мнимая полуось гиперболы; из уравнения видно, что гипербола не пересекает ось OY, т.е. 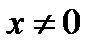 . Для построения гиперболы строят прямоугольник со сторонами 2а и 2b, с центром в начале координат. Проводят диагонали в прямоугольнике, которые являются асимптотами
. Для построения гиперболы строят прямоугольник со сторонами 2а и 2b, с центром в начале координат. Проводят диагонали в прямоугольнике, которые являются асимптотами 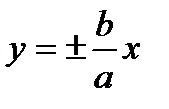 . Вершины гиперболы находятся в точках
. Вершины гиперболы находятся в точках 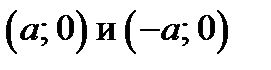 .
.
Замечание.Если уравнение гиперболы имеет вид : 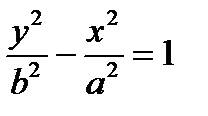 , то вершины гиперболы находятся на оси OY в точках
, то вершины гиперболы находятся на оси OY в точках 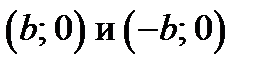 . Гиперболы называются сопряженными (у них действительная ось одной гиперболы служит мнимой осью другой, и наоборот; они имеют общие асимптоты). Если а= b, то уравнение принимает вид х2 – у2 = а2. Такая гипербола называется равнобочной. Ее асимптоты перпендикулярны друг к другу. Поэтому, если за координатные оси принять асимптоты равнобочной гиперболы, то ее уравнение примет вид:
. Гиперболы называются сопряженными (у них действительная ось одной гиперболы служит мнимой осью другой, и наоборот; они имеют общие асимптоты). Если а= b, то уравнение принимает вид х2 – у2 = а2. Такая гипербола называется равнобочной. Ее асимптоты перпендикулярны друг к другу. Поэтому, если за координатные оси принять асимптоты равнобочной гиперболы, то ее уравнение примет вид: 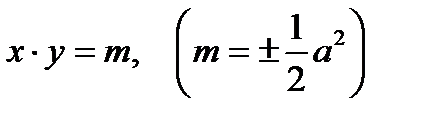 (рис. 9.3,а и рис. 9.3,б), или
(рис. 9.3,а и рис. 9.3,б), или 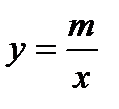 .
.
Рис. 9.3
4. Парабола – это множество точек плоскости, равноудаленных от данной точки, называемой фокусом, и от данной прямой, называемой директрисой (рис.9.4). Пусть прямая l: x=-p/2 является директрисой параболы, точка F(p/2,0) – фокус. Тогда каноническое уравнение параболы имеет вид: 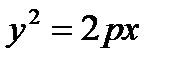 ,
,
где 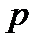 – фокальный параметр.
– фокальный параметр.
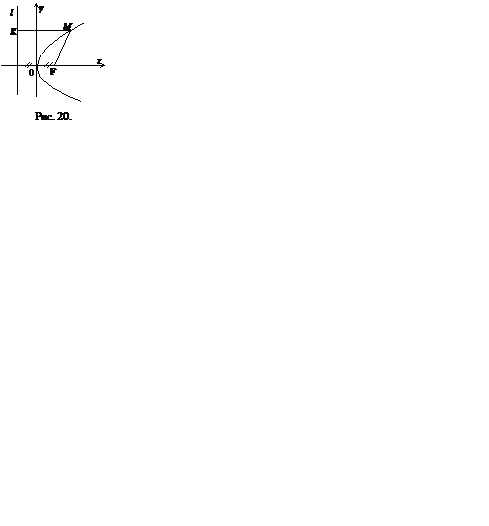
Рис. 9.4
Эта парабола расположена симметрично относительно оси ОХ ( 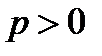 ),
), 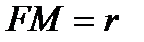 – фокальный радиус параболы, который определяется по формуле
– фокальный радиус параболы, который определяется по формуле 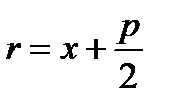 , так как
, так как 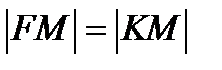 . Уравнение
. Уравнение 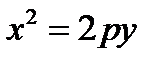 является уравнением параболы, симметричной относительно оси ординат ОУ. При р > 0 ветви параболы направлены в положительную сторону соответствующей координатной оси, а при р < 0 – в отрицательную сторону.
является уравнением параболы, симметричной относительно оси ординат ОУ. При р > 0 ветви параболы направлены в положительную сторону соответствующей координатной оси, а при р < 0 – в отрицательную сторону.
Приведение общего уравнения
Кривой второго порядка к
Каноническому виду
Если общее уравнение кривой второго порядка вида:
a11x2+a22y2 +2a1x+ 2a2y+a0=0 , т.е. не содержит члены с произведением xy ( a12=0 ), то следует выделить полные квадраты по x и по y :
a11(x2+2a1x/a11)+a22(y2+2a2y/a22)+a0=0,
a11(x2+2a1x/a11)+a22(y2+2a2y/a22)+a0=0,
a11(x2+2a1x/a11+(a1/a11)2)+a22(y2+2a2y/a22+(a2/a22)2)-
-(a1/a11)2-(a2/a22)2+a0=0
или
a11(x+a1/a11)2+a22(y+a2/a22)2=(a2/a22)2)+(a1/a11)2-(a2/a22)2-a0,
и сделать замену переменных (параллельный перенос)
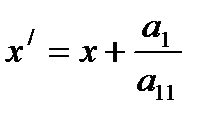 ,
, 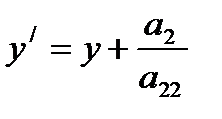 . Получим
. Получим 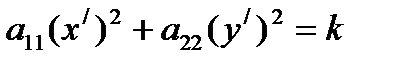 ,
,
где k=(a2/a22)2)+(a1/a11)2-(a2/a22)2-a0 или
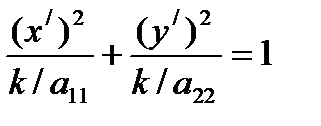 – канонический вид кривой второго порядка.
– канонический вид кривой второго порядка.
Дата: 2016-10-02, просмотров: 320.