Бисериальные коэффициенты корреляции оценивают зависимость между двумя признаками, один из которых измерен в шкале наименований с двумя градациями признака (дихотомической шкале). Бисериальные коэффициенты корреляции изменяются в диапазоне от -1 до +1, однако следует помнить, что в данном случае знак для интерпретации не имеет значения (это исключение из общего правила).
Рангово-бисериальный коэффициент корреляции используется в том случае, когда второй признак измерен по шкале порядка.
Расчет этого коэффициента производится по формуле:
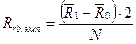
где 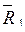 — средний ранг по тем элементам переменной Y, которым соответствует код 1 в переменной X;
— средний ранг по тем элементам переменной Y, которым соответствует код 1 в переменной X;
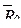 — средний ранг по тем элементам переменной Y, которым соответствует код 0 в переменной X;
— средний ранг по тем элементам переменной Y, которым соответствует код 0 в переменной X;
N — общее количество испытуемых.
Оценку значимости рангово-бисериального коэффициента корреляции произведем с помощью критерия Стьюдента.
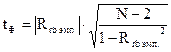
где 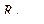 — расчетное значение рангово-бисериального коэффициента корреляции;
— расчетное значение рангово-бисериального коэффициента корреляции;
N — число испытуемых;
t Ф — расчетное значение критерия Стьюдента.
Расчеты рангово-бисериального коэффициента корреляции целесообразно вести в следующей таблице (таблица 18):
Таблица 18
| х i | yi | Ri | R1 | R0 |
| 1 | y1 | R1 | R1 | |
| 1 | y2 | R2 | R2 | |
| 0 | y3 | R3 | R3 | |
| 1 | y4 | R4 | R4 | |
| 0 | y5 | R5 | R5 | |
| 1 | y6 | R6 | R6 | |
| …… | …… | …… | …… | …… |
| 0 | yN | RN | RN | |
| ∑ R1 | ∑ R0 |
Правило принятия решения:
Табличное значение критерия Стьюдента находится по таблице критических значений в зависимости от числа степеней свободы (приложение 5). Число степеней свободы k = N -2.
Если расчетное значение критерия t Ф ≥ t табл., то между признаками существует статистическая значимая связь.
Если расчетное значение критерия t Ф ≤ t табл., то между признаками статистической связи нет.
Бисериальный коэффициент корреляции используется в том случае, когда второй признак измерен по шкале равных интервалов или шкале равных отношений. Расчет этого коэффициента производится по формуле:
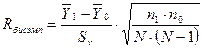
где 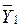 — среднее значение по тем элементам переменной Y, которым соответствует код 1 в переменной X;
— среднее значение по тем элементам переменной Y, которым соответствует код 1 в переменной X;
n 1 — количество значений 1 в переменной Х;
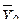 — среднее значение по тем элементам переменной Y, которым соответствует код 0 в переменной X;
— среднее значение по тем элементам переменной Y, которым соответствует код 0 в переменной X;
n 0 — количество значений 0 в переменной Х;
Sx — стандартное отклонение переменной Y;
N — общее количество испытуемых (N=n1+n0).
Оценку значимости рангово-бисериального коэффициента корреляции произведем с помощью критерия Стьюдента.
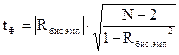
где 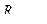 — расчетное значение бисериального коэффициента корреляции;
— расчетное значение бисериального коэффициента корреляции;
N — число испытуемых;
t Ф — расчетное значение критерия Стьюдента.
Расчеты бисериального коэффициента корреляции целесообразно вести в таблице следующего вида (таблица 19):
Таблица 19
| х i | yi | yi– 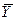
| (yi– 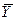 )2 )2
| yi1 | yi0 |
| 1 | y1 | y1 | |||
| 1 | y2 | y2 | |||
| 0 | y3 | y3 | |||
| 1 | y4 | y4 | |||
| 0 | y5 | y5 | |||
| 1 | y6 | y6 | |||
| …… | …… | …… | …… | ||
| 0 | yN | RN | |||
| ∑ yi | ∑ (yi– 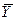 )2 )2
| ∑ y1 | ∑ y0 |
Правило принятия решения:
Табличное значение критерия Стьюдента находится по таблице критических значений в зависимости от числа степеней свободы (приложение 5). Число степеней свободы k = N -2.
Если расчетное значение критерия t Ф ≥ t табл., то между признаками существует статистическая значимая связь.
Если расчетное значение критерия t Ф ≤ t табл., то между признаками статистической связи нет.
Дата: 2019-11-01, просмотров: 313.