Нормальный закон[4] распределения во всех естественных науках имеет фундаментальное значение. И в психологических дисциплинах его значение трудно переоценить. Достаточно сказать, что все психологические шкалы основываются на этом законе, поскольку ему следуют распределения большинства человеческих способностей и свойств.

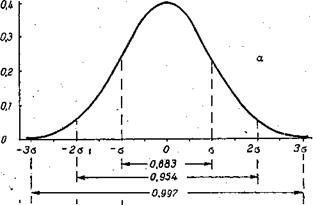
Рис. 14. Кривая нормального распределения

Самой общей характеристикой нормального распределения является простое наблюдение того закономерного факта, что очень большие центральные отклонения (x_i–M) встречаются крайне редко, а маленькие часто, при этом одинаковые по модулю отклонения одинаково вероятны. Такая закономерность может иметь место в условиях, когда на случайную величину х_i действует большое число разнообразных факторов и доля воздействия каждого из них одинаково мала по сравнению с их числом.

Свойства нормального распределения:

1. При всех значениях переменной х_i плотность положительна.

2. Плотность симметрична относительно математического ожидания, которое в этой связи нередко называют центром рассеивания (для симметричных распределений). Коэффициент асимметрии равен нулю.

3. При увеличении модуля аргумента кривая сколь угодно близко приближается к оси абсцисс, не достигая ее.

4. Численные значения среднего арифметического, моды и медианы совпадают.

5. Плотность нормального распределения быстро убывает по мере увеличения значений центрированной случайной величины, выраженных в единицах стандартного отклонения. Следует запомнить, что 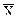 ± σ = 0,683;  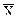± 2σ = 0,954;  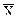± 3σ = 0,997.

6. При значениях – σ и + σ на кривой стандартной плотности на кривой дифференциального распределения) имеются точки смены кривизны (перегиба):                                на участке (– σ ≤ Х ≤ + σ) функция плотности вогнута вниз, а за его пределами, наоборот, вогнута вверх.

Несмотря на то, что теоретически нормальный закон распределения предполагает существование бесконечно малых и бесконечно больших значений любой, следующей ему величины, на практике (тем более в психологии) случайные переменные имеют конечные области существования. Поэтому на практике используются функции нормального распределения, ограниченные слева и справа основными отклонениями:        ± 4.

Гамма-распределение

Если воздействие одного или нескольких факторов из большого их числа, влияющего на случайную величину Х, значительно превосходит по силе воздействия все остальные факторы, то распределение случайной величины Х приобретает положительную асимметрию.

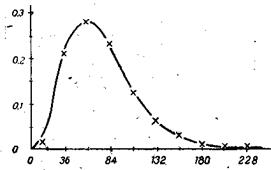
Рис. 15. Гамма-распределение

Гамма-распределение находит в психологии все более широкое применение благодаря тому, что большинство случайных временных интервалов, так или иначе характеризующих психическую активность, подчиняется именно этому распределению. В частности, время многих реакций человека подчинено гамма-распредлению. Ему следуют также общие (суммарные) затраты времени на последовательность рабочих действий, слабо зависящие (или не зависящие) друг от друга, причем величина этих затрат для разных действий может значительно варьировать, согласно условию, сформулированному выше.