Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

Назначения критерия

Критерий χ² применяется в двух целях;

1) для сопоставления эмпирического распределения признака с теоре­тическим (равномерным, нормальным или каким-то иным);

2) для сопоставления двух, трех или более эмпирических распределе­ний одного и того же признака, то есть для проверки их однородности;

3) для оценки стохастической (вероятностной) независимости в системе случайных событий;

и т.д.

Описание критерия

Критерий χ² отвечает на вопрос о том, с одинаковой ли частотой встречаются разные значения признака в эмпирическом и теоретическом распределениях или в двух и более эмпирических распределениях.

Преимущество метода состоит в том, что он позволяет сопостав­лять распределения признаков, представленных в любой шкале, начиная от шкалы наименований. В самом простом случае альтерна­тивного распределения ("да - нет", "допустил брак - не допустил бра­ка", "решил задачу - не решил задачу" и т. п.) мы уже можем приме­нить критерий χ².

Ограничения критерия

1. Объем выборки должен быть достаточно большим: N>30. При N<30 критерий χ² дает весьма приближенные значения. Точность крите­рия повышается при больших N.

2. Теоретическая частота для каждой ячейки таблицы не должна быть меньше 5: f ≥ 5. Это означает, что если число разрядов задано зара­нее и не может быть изменено, то мы не можем применять метод χ², не накопив определенного минимального числа наблюдений. Ес­ли, например, мы хотим проверить наши предположения о том, что частота обращений в телефонную службу Доверия неравномерно распределяются по 7 дням недели, то нам потребуется 5-7=35 обра­щений. Таким образом, если количество разрядов ( k ) задано зара­нее, как в данном случае, минимальное число наблюдений (N_min) оп­ределяется по формуле: .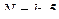

3. Выбранные разряды должны "вычерпывать" все распределение, то есть охватывать весь диапазон вариативности признаков. При этом группировка на разряды должна быть одинаковой во всех сопостав­ляемых распределениях.

4. Необходимо вносить "поправку на непрерывность" при сопоставле­нии распределений признаков, которые принимают всего 2 значения. При внесении поправки значение χ², уменьшается (см. пример с по­правкой на непрерывность).

5. Разряды должны быть неперекрещивающимися: если наблюдение отнесено к одному разряду, то оно уже не может быть отнесено ни к какому другому разряду. Сумма наблюдений по разрядам всегда должна быть равна общему количеству наблюдений.

Алгоритм расчета критерия χ²

1. Составить таблицу взаимной сопряженности значений признаков следующего вида (по сути это двумерный вариационный ряд, в котором указываются частоты появления совместных значений признака) — таблица 14. В таблице располагаются условные частоты, которые мы обозначим в общем виде как f_ij. Например, число градаций признака х равно 3 (k=3), число градаций признака у равно 4 (m=4); тогда i меняется от 1 до k, а j меняется от 1 до m.

                                                                                                                    Таблица 15

х у	х1	х2	х3	∑
у1	f11	f21	f31	f –1
у2	f12	f22	f32	f –2
у3	f13	f23	f33	f –3
у4	f14	f24	f34	f –4
∑	f1–	f2–	f3–	N

2. Далее для удобства расчетов преобразуем исходную таблицу взаимной сопряженности в таблицу следующего вида (таблица 16), располагая столбики с условными частотами один под другим: Занести в таблицу наименования разрядов (столбцы 1 и 2) и соответствующие им эмпирические частоты (3-й столбец).

                                                                                                             Таблица 16

х	у	fij	fij*	fij – fij*	(fij – fij*)2	(fij – fij*)2/ fij*
1	2	3	4	5	6	7
х1	у1	f11	f11*
х1	у2	f12	f12*
х1	у3	f13	f13*
х1	у4	f14	f14*
х2	у1	f21	f21*
х2	у2	f22	f22*
х2	у3	f23	f23*
х2	у4	f24	f24*
х3	у1	f31	f31*
х3	у2	f32	f32*
х3	у3	f33	f33*
х3	у4	f34	f34*
						∑=………….

3. Рядом с каждой эмпирической частотой записать теоретическую частоту (4-й столбец), которая вычисляется по следующей формуле (итоговая частоты по соответствующей строчке умножается на итоговую частоту по соответствующему столбику и делится на общее количество наблюдений):

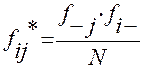
4. Подсчитать разности между эмпирической и теоретической частотой по каждому разряду (строке) и записать их в 5-й столбец.

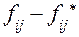
5. Определить число степеней свободы по формуле: ν =( k -1)( m -1) , где k - количество разрядов признака х, m — количество разрядов признака у. 

Если ν=1, внести поправку на "непрерывность" и записать её в столбце 5а.

Поправка на непрерывность состоит в том, что от разности между условной и теоретической частотой отнимается еще 0,5. Тогда заголовки столбиков в нашей таблице будет выглядеть следующим образом:

                                                                                                                Таблица 17

х	у	fij	fij*	fij – fij*	fij – fij * – 0,5	(fij – fij* – 0,5)2	(fij – fij* – 0,5)2/ fij*
1	2	3	4	5	5а	6	7

6. Возвести в квадрат полученные разности и занести их в 6-й столбец.

7. Разделить полученные квадраты разностей на теоретическую часто­ту и записать результаты в 7-й столбец.

8. Просуммировать значения 7-го столбца. Полученную сумму обо­значить как χ²_эмп.

9. Правило принятия решения:

Расчетное значение критерия необходимо сравнить с критическим (или табличным) значением. Критическое значение находится в зависимости от числа степеней свободы по таблице критических значений критерия χ² Пирсона.

Если χ²_расч ≥ χ²_табл , то рас­хождения между распределениями статистически достоверны, или признаки изменяются согласованно, или связь между признаками статистически значима.

Если χ²_расч < χ²_табл , то расхождения между рас­пределениями статистически недостоверны, или признаки изменяются несогласованно, или связи между признаками нет.

 

       Прежде чем рассматривать меры связи дальше, необходимо освоить такую процедуру как ранжирование.

 

Ранжирование

 

Ранжирование — это процедура, при которой значения признака заменяются рангами.

Ранг — это порядковое место значения в упорядоченном ряду всех значений.

Правила ранжирования

1. Меньшему значению присваивается меньший ранг.                                                      Наименьшему значению начисляется ранг 1.                                                                    Наибольшему значению начисляется ранг, соответствующий количеству ранжируемых значений, за исключением тех случаев, которые предусмотрены правилом 2.                    

Если, например, N=7, то наибольшее значение получит ранг 7 (за исключением тех случаев, которые описаны правилом 2).

2. В случае, если несколько значений равны, им начисляется ранг, представляющий собой среднее значение из тех рангов, которые они получили бы, если бы были не равны.       

Например, три наименьших значения равны 15 секундам. Следующее значение в ряду значений равно 17 секундам. Первые три равных значения занимают в ряду 1-е, 2-е и 3-е места, на 4-м месте стоит следующее по величине значение — 17 секунд и т.д. Каждое из равных значений получает средний ранг 2, а значение 17 — ранг 4.

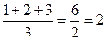
Допустим, следующие два значения равны 19 секундам. Они занимают 5-е и 6-е места в ряду значений и должны были бы получить 5-й и 6-й ранги, если бы были не равны. Но, поскольку они равны, то получают средний ранг, равный 5,5.

                                 

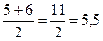
3. Общая сумма проставленных рангов должна совпадать с расчетной суммой рангов, которая определяется по формуле:

где N — общее количество ранжируемых наблюдений (значений).

Несовпадение реальной и расчетной сумм рангов свидетельствует об ошибке, допущенной при начислении рангов и/или их суммировании. Поэтому прежде чем продолжить работу необходимо найти ошибку и устранить ее.