Зависимость (взаимосвязь) между случайными событиями состоит в том, что появление одного из событий изменяет вероятность появления другого события.
Факт взаимосвязи между случайными событиями состоит в совместном изменении меры возможностей их появления (частоты, частости, вероятности). По наличию или отсутствию такого изменения и судят о наличии или отсутствии зависимости между событиями. Это изменение устанавливается на основе анализа двумерного вариационного ряда или таблицы сопряженности.
Например, у некоторой группы людей измерялись два признака. Признак xi, который может принимать одно из четырех значений, и признак yj, который может принимать одно из трех значений. В этом случае таблица сопряженности будет выглядеть следующим образом:
Таблица 12
| xi yj | x 1 | x 2 | x 3 | x 4 | S |
| y 1 | f11 | f21 | f31 | f41 | f-1 |
| y 2 | f12 | f22 | f32 | f42 | f-2 |
| y 3 | f13 | f23 | f33 | f43 | f-3 |
| S | f1- | f2- | f3- | f4- | N |
В этой таблице внутри прямоугольника, выделенного жирной чертой, находятся частоты fij, которые отражают число людей в выборке, имеющих какое-то значение xi при условии, что y = yj . Эти частоты называются условными частотами.
Сумма частот по столбикам обозначена как fi - — это безусловные частоты признака xi. Они показывают, сколько человек в выборке имеют значение xi безотносительно к значениям признака у.
Сумма частот по столбикам обозначена как f - j — это безусловные частоты признака уi. Они показывают, сколько человек в выборке имеют значение уi безотносительно к значениям признака х.
На основании таких таблиц сопряженности рассчитываются многие меры связи.
Взаимосвязи между признаками характеризуются силой связи и ее направлением. О силе взаимосвязи свидетельствует абсолютное значение расчетной меры связи: чем она больше, тем сильнее взаимосвязь. О направлении взаимосвязи мы судим по знаку расчетной меры связи[5]: положительный знак — взаимосвязь прямая или положительная, отрицательный знак — взаимосвязь обратная или отрицательная.
Проиллюстрировать направление взаимосвязей можно при помощи следующего рисунка.
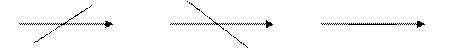
Рис. 17. Диаграммы рассеивания первичных данных для случаев различных взаимосвязей между ними
Предположим, у некоторой группы испытуемых измерены два признака — X (ось абсцисс) и Y (ось ординат). Каждый испытуемый на такой двумерной плоскости займет строго определенное место в зависимости от сочетания значений признаков X и Y у данного человека.
На графике слева показана диаграмма рассеивания для случая положительной зависимости между признаками (рост значений одного признака сочетается с ростом значений другого признака).
Средний график иллюстрирует отрицательную зависимость: рост значений одного признака сочетается с уменьшением значений другого признака.
График справа — отсутствие зависимости: четкой закономерности сочетания значений признаков не прослеживается, встречаются любые варианты.
Взаимосвязи характеризуются двумя свойствами: силой и направлением. О силе взаимосвязи мы судим по абсолютной величине данной меры: чем она больше, тем сильнее взаимосвязь. На направление зависимости (прямая или обратная взаимосвязь) нам указывает знак данной меры: положительный знак свидетельствует о прямой зависимости, отрицательный знак — об обратной.
Для принятия решения о наличии или отсутствии взаимозависимости между признаками в корреляционном анализе существует правило вывода: Расчетное значение по абсолютной величине сравнивается с табличным значением. Если оно больше или равно критическому (табличному) значению, то делается вывод о наличии взаимозависимости (или взаимосвязь между признаками статистически значима, или взаимосвязь между признаками статистически достоверна). При этом обязательно указывается уровень значимости вывода: при р=0,95 или a =0,05 (более слабая взаимосвязь) или р=0,99 или a=0,01 (более сильная взаимосвязь).
Для облегчения задачи выбора меры связи, адекватной данному случаю, целесообразно воспользоваться таблицей 13. В этой таблице меры связи приведены в соответствие тем измерительным шкалам, по которым измерены признаки, между которыми необходимо найти взаимосвязь.
Таблица 13
Общий обзор мер связи
|
Измерительные шкалы | Шкала наименований | Шкала порядка | Интервальная, пропорциональная шкалы | ||
| k = 2 | k > 2 | ||||
|
Шкала наименований | k = 2 | Коэффициент контингенции j | |||
| k > 2 | Критерий c 2 |
Коэффициент взаимной сопряженности Чупрова К Коэффициент взаимной сопряженности Пирсона С
| |||
|
Шкала порядка | Рангово-бисериальный коэффициент корреляции rRbis |
Ранговые коэффициенты корреляции: Спирмена r Кендэлла t | |||
|
Интервальная, пропорциональная шкалы | Бисериальный коэффициент корреляции rbis | Коэффициент линейной корреляции Пирсона r Корреляционное отношение h | |||
Коэффициент контингенции
Если оба признака измерены по шкале наименований и каждый из них может иметь только два значения, то мерой связи является коэффициент контингенции «фи» — φ. В некоторых книгах по статистике этот коэффициент называется четырехклеточный коэффициент или четырехпольный коэффициент, или тетрахорический показатель связи.
Удобнее всего этот коэффициент рассчитывать по 4-хпольной таблице сопряженности признаков (таблица 14) — таблице, показывающей частоту совместного появления у испытуемых пар значений по 2-м признакам.
Таблица 14
| Значение признаков | X1 = 0 | X2 = 1 | Σ |
| Y1 = 0 | f00 = a | f10 = b | a + b |
| Y2 = 1 | f01 = c | f11 = d | c + d |
| Σ | a + c | b + d | N = a + b + c + d |
Расчетное значение коэффициента контингенции вычисляется по следующей формуле:
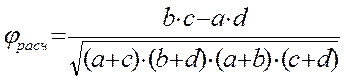
Поскольку таблиц с критическими значениями для данного коэффициента не существует, то значимость этой меры связи оценивают при помощи критерия χ2.
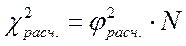
Правило принятия решения:
Расчетное значение критерия необходимо сравнить с критическим (или табличным) значением. Критическое значение находится в зависимости от числа степеней свободы (приложение с таблицами критических значений). Однако, для 4-хпольной таблицы число степеней свободы всегда равно 1 (ν = 1), поэтому можно привести эти значения, которыми всегда следует пользоваться для 4-хклеточных таблиц: χ2табл. = 3,84 для р = 0,95 и = 6,64 для р = 0,99.
Если χ2расч ≥ χ2табл , то связь между признаками статистически значима, т. е. признаки изменяются согласованно. О направлении зависимости свидетельствует знак коэффициента взаимной сопряженности φ.
Если χ2расч < χ2табл , то связи между признаками нет.
Дата: 2019-11-01, просмотров: 325.