Тема 5. Решение задачи сравнения выборок. Понятие статистических критериев и их виды
Сравнение распределений: проверка гипотез. Понятие статистической гипотезы. Нулевая и альтернативная гипотезы. Направленная и ненаправленная гипотезы.
Статистические критерии. Основные распределения, используемые при проверке статистических гипотез в социальных и психологических исследованиях. Таблицы критических значений. Число степеней свободы. Уровни статистической значимости. Правило отклонения нулевой гипотезы и принятия альтернативной гипотезы: зона незначимости, зона неопределенности и зона значимости. Мощность критериев. Зависимые и независимые выборки.
Параметрические и непараметрические критерии. Возможности и ограничения параметрических и непараметрических критериев.
Методические рекомендации к изучению темы
При изучении данной темы необходимо обратить внимание на сущность статистических гипотез и этапы принятия статистического решения.
Особое внимание следует обратить на следующий материал: статистическая значимость, число степеней свободы, классификация критериев различий и область их применения. Внимательно изучите этот материал и попытайтесь самостоятельно придумать примеры психологических исследований, в которых можно было бы применить каждый из критериев различий, приведенных в таблицах 1 и 2 (Общий обзор критериев).
После изучения материала лекции ответьте на контрольные вопросы и выполните самостоятельное задание, ответы занесите в конспект.
Материалы лекции.
Статистические гипотезы
Полученные в исследованиях выборочные данные всегда ограничены и носят в значительной мере случайный характер. Именно поэтому для анализа таких данных и используется математическая статистика, позволяющая обобщать закономерности, полученные на выборке, и распространять их на всю генеральную совокупность.
Подчеркнем еще раз, что полученные в результате эксперимента на какой-либо выборке данные служат основанием для суждения о генеральной совокупности. Однако в силу действия случайных вероятностных причин оценка параметров генеральной совокупности, сделанная на основании экспериментальных (выборочных) данных, всегда будет сопровождаться погрешностью, и поэтому подобного рода оценки должны рассматриваться как предположительные, а не как окончательные утверждения.
Как указывает Г.В. Суходольский: «Под статистической гипотезой обычно понимают формальное предположение о том, что сходство (или различие) некоторых параметрических или функциональных характеристик случайно или, наоборот, неслучайно»[10]. Подобные предположения о свойствах и параметрах генеральной совокупности, различии выборок или зависимости между признаками получили названиестатистических гипотез.
Сущность проверки статистической гипотезы заключается в том, чтобы установить, согласуются ли экспериментальные данные и выдвинутая гипотеза, допустимо ли отнести расхождение между гипотезой и результатом статистического анализа экспериментальных данных за счет случайных причин? Таким образом, статистическая гипотеза — это научная гипотеза, допускающая статистическую проверку, а математическая статистика — это научная дисциплина, задачей которой и является научно обоснованная проверка статистических гипотез.
При проверке статистических гипотез используются два понятия: так называемая нулевая (обозначение Н0) и альтернативная гипотеза (обозначение Н1).
При сравнении распределений принято считать, что нулевая гипотеза Н0 — это гипотеза о сходстве, а альтернативная Н1 — гипотеза о различии. Таким образом, принятие нулевой гипотезы Н0 свидетельствует об отсутствии различий, а гипотезы Н1 — о наличии различий.
Например, две выборки извлечены из нормально распределенных генеральных совокупностей и перед нами стоит задача сравнить эти выборки. Одна выборка имеет параметры 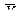 и σ1, а другая параметры
и σ1, а другая параметры 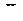 и σ2. Нулевая гипотеза Н0 исходит из предположения о том, что
и σ2. Нулевая гипотеза Н0 исходит из предположения о том, что 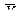 =
= 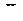 и σ1=σ2, то есть разность двух средних
и σ1=σ2, то есть разность двух средних 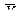 –
– 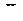 =0 и разность двух стандартных отклонений σ1–σ2,=0 (отсюда и название гипотезы — нулевая).
=0 и разность двух стандартных отклонений σ1–σ2,=0 (отсюда и название гипотезы — нулевая).
Принятие альтернативной гипотезы Н1 свидетельствует о наличии различий и исходит из предположения, что 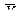 –
– 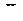 ≠0 и σ1–σ2,≠0.
≠0 и σ1–σ2,≠0.
Очень часто альтернативная гипотеза носит название экспериментальной гипотезы, если в исследовании ставится задача доказать существование различий между выборками. Если же исследователь хочет доказать именно отсутствие различий, то экспериментальной гипотезой является нулевая гипотеза.
При сравнении выборок альтернативные статистические гипотезы могут быть направленными и ненаправленными.
Если мы заметили, что в одной выборке индивидуальные значения испытуемых по какому-либо признаку, выше, а в другой — ниже, то для проверки различий между выборками формулируется направленная гипотеза. Если мы ходим доказать, что в одной группе под влиянием каких-то экспериментальных воздействий произошли более выраженные изменения, необходимо также сформулировать направленную гипотезу. Формально она записывается так Н1: х1 превышает х2. Нулевая гипотеза при этом выглядит следующим образом Н0: х1 не превышает х2.
Если мы хотим доказать, что различаются формы распределения, то формулируются ненаправленные гипотезы. Формально они записывается так Н1: х1 отличается от х2. Нулевая гипотеза Н0: х1 не отличается от х2.
Вообще говоря, при принятии или отвержении гипотез возможны различные варианты.
При проверке гипотезы экспериментальные данные могут противоречить гипотезе Н0, тогда эта гипотеза отклоняется. В противном случае, т.е. если экспериментальные данные согласуются с гипотезой Н0, она не отклоняется. Часто в таких случаях говорят, что гипотеза Н0 принимается (хотя такая формулировка не совсем точна, однако она широко распространена). Отсюда видно, что статистическая проверка гипотез, основанная на экспериментальных, выборочных данных, неизбежно связана с риском (вероятностью) принять ложное решение. При этом возможны ошибки двух родов. Ошибка первого рода произойдет, когда будет принято решение отклонить гипотезу Н0, хотя в действительности она оказывается верной. Ошибка второго рода произойдет когда будет принято решение не отклонять гипотезу Н0, хотя в действительности она будет неверна. Очевидно, что и правильные выводы могут быть приняты также в двух случаях. Вышесказанное можно представить в виде таблицы 27.
Таблица 27
| Гипотезы Результат проверки | Возможные состояния проверяемой гипотезы | |
| Верна гипотеза Н0 | Верна гипотеза Н1 | |
| Гипотеза Н0 отклоняется | Ошибка первого рода | Правильное решение |
| Гипотеза Н0 не отклоняется | Правильное решение | Ошибка второго рода |
Поскольку исключить ошибки при принятии статистических гипотез невозможно, то необходимо минимизировать возможные последствия, т.е. принятие неверной статистической гипотезы. В большинстве случаев единственный путь минимизации ошибок заключается в увеличении объема выборки.
Дата: 2019-11-01, просмотров: 385.