В практике математико-статистического анализа результатов психологических исследований нередко встает задача проверки, является ли полученное в исследовании эмпирическое распределение нормальным (например, при выборе параметрического критерия Стьюдента для сравнения средних арифметических значения; или при решении использовать для анализа какой-либо из многомерных методов). Ответ на этот вопрос важен, потому что одним из условий адекватного применения данных методов и является нормальность эмпирических распределений.
Чтобы установить является ли эмпирическое распределение изучаемой случайной величины нормальным, необходимо сопоставить сведения о свойствах этой величины и условиях ее изучения, известные исследователю, со свойствами функции нормального распределения. Это сопоставление вначале является качественным, а затем осуществляется специальными количественными методами.
Основой качественного сопоставления служит основное "физическое" условие появления нормального распределения: действие на изучаемую величину большого числа факторов, тоже случайных, воздействия которых преимущественно независимы и примерно одинаковы.
Если такое условие имеет место, то можно ожидать, что изучаемая случайная величина распределена нормально. Например, на формирование способностей человека действует множество различных случайных факторов (биологических, физиологических, психических и социальных). Поэтому можно ожидать, что в массе людей степень выраженности той или иной способности распределена нормально. Это во многом подтверждается практикой тестирования способностей.
Количественное сопоставление включает два последовательных этапа.
Первый — сравнение отдельных свойств эмпирического распределения со свойствами нормального закона. Это касается, прежде всего:
симметричности (мода, медиана и среднее арифметическое примерно или точно одинаковы),
весьма информативным является факт наличия точек смены кривизны на сглаженном от руки полигоне распределения при значениях случайной величины, равных – σ и + σ и др.
Если имеется соответствие между некоторыми из перечисленных свойств эмпирического и нормального распределений, то можно перейти к следующему этапу.
Второй этап — количественный — может выполняться двумя способами: точная оценка с помощью критериев согласия распределений и приближенная оценка по параметрам изменчивости.
Точная количественная оценка нормальности распределения может быть выполнена с помощью критерия Колмогорова-Смирнова (см. тему критерии согласия распределений). Для применения этого критерия необходимо вычислить значения теоретической функции распределения по эмпирическому ряду в предположении, что он подчиняется нормальному закону. Именно это предположение и обосновывается при качественном и количественном (на первом этапе) сопоставлении свойств.
Вычисление теоретических значений вероятностей, соответствующих эмпирическим частостям, в общем случае вычисляется либо по таблицам функций распределения, либо через логарифмы, либо с использованием таблиц специальных функций. Нередки комбинации последних двух способов.
В предположении нормального закона обычно пользуются таблицами функций f(x) и F(x). Суть вычисления вероятностей здесь такова. Осуществляют преобразование значений xi случайной величины Х в основные (стандартные) отклонения
 |  |
Для чего, разумеется, предварительно следует по эмпирическому ряду вычислить оценки
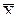и s. Далее по таблице "Значение функции распределения F(x) плотности f(x) нормального закона" для всех zi эмпирического ряда определяют значения стандартной плотности f(x), которые затем умножают на отношение
 |
чтобы от стандартного перейти к истинному (опытному) масштабу функций распределения, или значению функции распределения F(x):
и
Сопоставление заканчивается сравнением фактических (полученных в опыте) частостей и теоретических (вычисленных) вероятностей. Если различия малы или отсутствуют, то можно считать, что изучаемая случайная величина распределена нормально. Лишенная субъективных предпочтений оценка того, "малы" или "велики" получившиеся различия, осуществляется с помощью специальных критериев согласия (например, Колмогорова-Смирнова).
Приближенная количественная оценка нормальности распределения выполняется на основе расчета таких параметров изменчивости как коэффициент асимметрии и коэффициент эксцесса, а также вычисления ошибок этих параметров.
Ошибка коэффициента асимметрии рассчитывается по следующим формулам:
А) приближенно при больших N
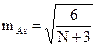
Б) точно
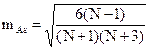
Ошибка коэффициента эксцесса вычисляется по формулам:
А) приближенно при больших N
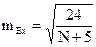
Б) точно
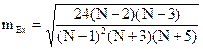
Далее необходимо найти соотношение параметра и его ошибки:
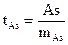и 
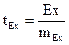
Если tAs и tEx больше или равно 3, то распределение отличается от нормального.
Если tAs и tEx меньше 3, то распределение можно считать нормальным.
Дата: 2019-11-01, просмотров: 255.
