Коэффициент взаимной сопряженности Пирсона С также является мерой связи двух признаков, если один из них измерен по шкале наименований и может иметь несколько значений (больше двух), а второй признак измерен по такой же шкале или по шкале порядка, или по шкале интервальной, или по шкале пропорциональной.

       Этот коэффициент также рассчитывается с помощью критерия хи-квадрат Пирсона, расчетное значение которого подставляется в формулу:

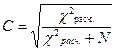, где N — общий объем выборки.

       Таблиц с критическими значениями для коэффициента взаимной сопряженности Пирсона не существует. Поэтому поступают следующим образом:

1. Вычисляют расчетное значение критерия хи-квадрат Пирсона.

2. Сравнивают его с критическим значением для соответствующего числа степеней свободы.

3. Если χ²_расч < χ²_табл , то расхождения между рас­пределениями статистически недостоверны, или признаки изменяются несогласованно, или связи между признаками нет. Делается вывод об отсутствии взаимосвязи. Величину коэффициента С можно в этом случае не вычислять.

4. Если χ²_расч ≥ χ²_табл , то рас­хождения между распределениями статистически достоверны, или признаки изменяются согласованно, или связь между признаками статистически значима.

5. Далее вычисляется значение коэффициента взаимной сопряженности Пирсона, которое и является мерой связи. Чем больше это значение (величина этого коэффициента может быть только положительной и изменяется от 0,00 до +1,00), тем сильнее взаимосвязь.

Обратите внимание на то, что ограничения в использовании этого коэффициента соответствуют ограничениям критерия хи-квадрат Пирсона, а именно: объем выборки должен быть N≥30 и теоретическая частота в ячейках должна быть f≥ 5.

Сравнение двух последних коэффициентов показало, что в одних и тех же случаях коэффициент взаимной сопряженности Пирсона дает несколько бóльшие значения меры связи.

Следует учитывать при выборе меры связи и то, что коэффициент взаимной сопряженности Чупрова рекомендуется использовать в тех случаях, когда число градаций значений признаков невелико, так как этот коэффициент менее чевствителен к количеству событий.

Ранговой коэффициент корреляции Спирмена

Метод ранговой корреляции Спирмена позволяет определить тес­ноту (силу) и направление корреляционной связи между двумя призна­ками или двумя профилями (иерархиями) признаков.

Для подсчета коэффициента ранговой корреляции ранговой корреляции ρ (другое обозначение r_s) необходимо располагать двумя рядами значений, которые могут быть проранжированы. Такими рядами значений мо­гут быть:

1) два признака, измеренные в одной и той же группе испытуемых;

2) две индивидуальные иерархии признаков, выявленные у двух испы­туе­мых по одному и тому же набору признаков (например, личност­ные профили по 16-факторному опроснику Р. Б. Кеттелла, иерархии ценностей по методике Р. Рокича, последовательности предпочтений в выборе из нескольких альтерна­тив и др.);

3) две групповые иерархии признаков;

4) индивидуальная и групповая иерархии признаков.

Во всех четырех случаях значимость полученного коэффициента корреля­ции определяется по количеству ранжированных значений N. В первом случае это количество будет совпадать с объемом выборки N — количеством испытуемых. Во втором случае коли­чеством наблюдений будет количество признаков, составляющих иерархию. В третьем и четвертом случае N — это также количество сопоставляемых призна­ков, а не количество испытуемых в группах.

Коэффициент ранговой корреляции может изменяться от –1 до +1. Положительный знак свидетельствует о прямой зависимости, отрицательный знак — об обратной.

Если абсолютная величина ρ, достигает критического (табличного) значения или пре­вышает его, корреляция достоверна.