Поможем в ✍️ написании учебной работы

Имя

Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой

Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно - исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое

Нажимая кнопку "Продолжить", я принимаю политику конфиденциальности

КОНСПЕКТ 7

7.1 КРИВЫЕ ВТОРОГО ПОРЯДКА.

Кривая второго порядка может быть задана уравнением

Ах² + 2Вху + Су² + 2Dx + 2Ey + F = 0.

       Существует система координат (не обязательно декартова прямоугольная), в которой данное уравнение может быть представлено в одном из видов, приведенных ниже.

1) 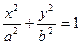 - уравнение эллипса.

2) 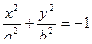 - уравнение “мнимого” эллипса.

3) 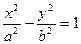 - уравнение гиперболы.

4) a²x² – c²y² = 0 – уравнение двух пересекающихся прямых.

5) y² = 2px – уравнение параболы.

6) y² – a² = 0 – уравнение двух параллельных прямых.

7) y² + a² = 0 – уравнение двух “мнимых” параллельных прямых.

8) y² = 0 – пара совпадающих прямых.

9) (x – a)² + (y – b)² = R² – уравнение окружности.

 

7.1.1 ОКРУЖНОСТЬ

 

В окружности (x – a)² + (y – b)² = R² центр имеет координаты (a; b).

 

Пример 1

       Найти координаты центра и радиус окружности, если ее уравнение задано в виде:

2x² + 2y² – 8x + 5y – 4 = 0.

 

       Для нахождения координат центра и радиуса окружности данное уравнение необходимо привести к виду, указанному выше в п.9. Для этого выделим полные квадраты:

x² + y² – 4x + 2,5y – 2 = 0

x² – 4x + 4 –4 + y² + 2,5y + 25/16 – 25/16 – 2 = 0

(x – 2)² + (y + 5/4)² – 25/16 – 6 = 0

(x – 2)² + (y + 5/4)² = 121/16

 

Отсюда находим О(2; -5/4); R = 11/4.

7.1.2 ЭЛЛИПС

Эллипсом называется линия, заданная уравнением .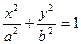

 

 Фокусами называются такие две точки, сумма расстояний от которых до любой точки эллипса есть постоянная величина.

 

                                                                      

 

                                                                             М

                                                            r₁                                                        

                                                                         r₂

                                                      F₁      O    F₂                  х

 

F₁, F₂ – фокусы. F₁ = (c; 0); F₂(-c; 0)

с – половина расстояния между фокусами;

a – большая полуось;

b – малая полуось.

Теорема Фокусное расстояние и полуоси эллипса связаны соотношением:

a² = b² + c².

Форма эллипса определяется характеристикой, которая является отношением фокусного расстояния к большей оси и называется эксцентриситетом.

Е = с/a.

Т.к. с < a, то е < 1.

       С эллипсом связаны две прямые, называемые директрисами. Их уравнения:

x = a/e; x = -a/e.

Пример 2

Составить уравнение прямой, проходящей через левый фокус и нижнюю вершину эллипса, заданного уравнением: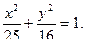

 

1) Координаты нижней вершины: x = 0; y² = 16; y = -4.

2) Координаты левого фокуса: c² = a² – b² = 25 – 16 = 9; c = 3; F₂(-3; 0).

3) Уравнение прямой, проходящей через две точки:

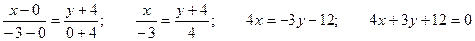
Пример 3

Составить уравнение эллипса, если его фокусы F₁(0; 0), F₂(1; 1), большая ось равна 2.

       Уравнение эллипса имеет вид: 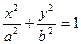. Расстояние между фокусами:

2c = 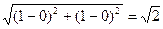, таким образом, a² – b² = c² = ½

по условию 2а = 2, следовательно а = 1, b =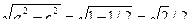  

Итого: .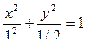

 

 

7.1.3 ГИПЕРБОЛА

       Определение. Гиперболой называется множество точек плоскости, для которых модуль разности расстояний от двух данных точек, называемых фокусами есть величина постоянная, меньшая расстояния между фокусами.

 

 

                                                                  y

 

                                                                                                           M(x, y)

                                                                   b

                                                                    r₁

                                                                                                     r₂

                                                                                                                            x

 

                                 F₁                                     a   F₂

 

 

с

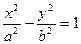    - Каноническое уравнение гиперболы.

Гипербола симметрична относительно середины отрезка, соединяющего фокусы и относительно осей координат.

       Ось 2а называется действительной осью гиперболы.

       Ось 2b называется мнимой осью гиперболы.

Гипербола имеет две асимптоты, уравнения которых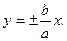

Отношение 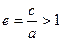называется эксцентриситетом гиперболы, где с – половина расстояния между фокусами, а – действительная полуось.

С учетом того, что с² – а² = b²:

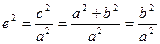
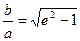
       Если а = b, e = 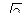, то гипербола называется равнобочной (равносторонней).

 

Две прямые, перпендикулярные действительной оси гиперболы и расположенные симметрично относительно центра на расстоянии a/e от него, называются директрисами гиперболы. Их уравнения: .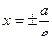

Пример 4

Найти уравнение гиперболы, вершины и фокусы которой находятся в соответствующих вершинах и фокусах эллипса .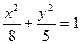

Для эллипса: c² = a² – b².

Для гиперболы: c² = a² + b².

 

                                                                                                    

 

                                                     

 

                               

                                                                                         

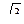
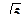
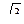
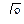
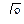
Уравнение гиперболы: .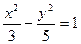

7.1.4 ПАРАБОЛА

Параболой называется множество точек плоскости, каждая из которых находится на одинаковом расстоянии от данной точки, называемой фокусом, и от данной прямой, называемой директрисой и не проходящей через фокус.

           

Расположим начало координат посередине между фокусом и директрисой.

 

                                                      у

                                А                    М(х, у)

 

                                                О        F                                                x

                                          p/2       p/2

 

 

Величина р (расстояние от фокуса до директрисы) называется параметром параболы.

y² = 2px

 

       Уравнение директрисы: x =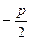

Пример 5

 На параболе у² = 8х найти точку, расстояние которой от директрисы равно 4.

 

       Из уравнения параболы получаем, что р = 4.

r = x + p/2 = 4; следовательно:

x = 2; y² = 16; y = ±4. Искомые точки: M₁(2; 4), M₂(2; -4).

 

ПРАКТИКУМ 7

ЗАДАНИЕ N 1
Тема: Кривые второго порядка
Известно, что уравнение параболы имеет вид 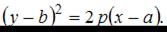Тогда уравнением параболы, изображенной на чертеже,

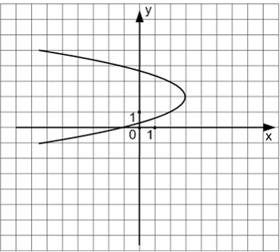
является …

Решение:
Каноническое уравнение параболы имеет вид: 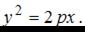С учетом параллельного переноса данное уравнение может быть записано в виде 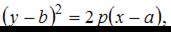где точка 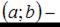вершина параболы. Исходя из чертежа можно записать уравнение 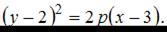Учтем, что парабола проходит, например, через точку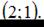
Тогда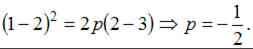
Тогда уравнение параболы примет вид: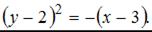

ЗАДАНИЕ N 2
Тема: Кривые второго порядка
Известно, что уравнение параболы имеет вид 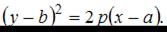Записать уравнение параболы, изображенной на чертеже:

 

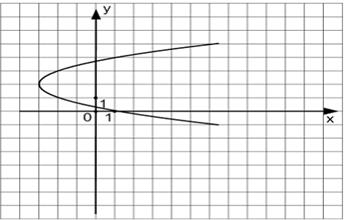
Решение:
Каноническое уравнение параболы имеет вид: С учетом параллельного переноса данное уравнение может быть записано в виде 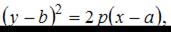где точка 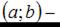вершина параболы. Исходя из чертежа можно записать уравнение 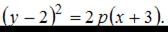Учтем, что парабола проходит, например, через точку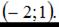
Тогда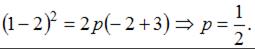
Тогда уравнение параболы примет вид: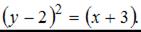

ЗАДАНИЕ N 3
Тема: Кривые второго порядка
Уравнением окружности, изображенной на чертеже,

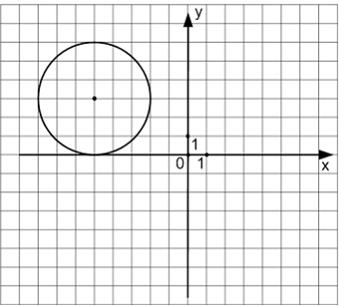
является …

 

Решение:
Из чертежа видно, что центр окружности имеет координаты (−5; 3) и ее радиус равен 3. Подставим эти данные в уравнение окружности 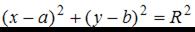и получим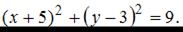

 

 

ЗАДАНИЕ N 4

На правой ветви гиперболы 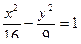найти точку, расстояние которой от правого фокуса в два раза меньше её расстояния от левого фокуса.

Решение:

 Для правой ветви гиперболы фокальные радиусы - векторы определяются по формулам r1 = ex- а и r2 = ex + а. Следовательно, имеем уравнение ех + а = 2(ех - а), откуда х = 3а/e; здесь а = 4, е = с/a = 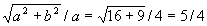, т.е. х = 9,6

Ординату находим из уравнения гиперболы:

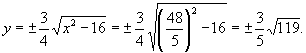
Таким образом, условию задачи удовлетворяют две точки: М1(9,6; 0,6 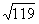) и М2(9,6;-0,6 ).

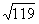ЗАДАНИЕ N 5

Эксцентриситет гиперболы равен 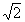. Составить простейшее уравнение гиперболы, проходящей через точку М( ).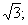

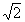Решение:

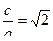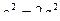 Согласно определению эксцентриситета, имеем , или . Но 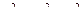; следовательно 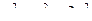, или 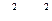, т.е. гипербола равнобочная.

Другое равенство получим из условия нахождения точки М на гиперболе, т.е.

 

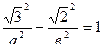, или 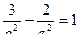. Поскольку 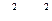, получим 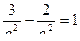, т.е.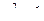

Таким образом, уравнение искомой гиперболы имеет вид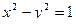

 

 

САМОСТОЯТЕЛЬНАЯ РАБОТА 7

ЗАДАНИЕ N 1
Тема: Кривые второго порядка
Известно, что уравнение параболы имеет вид 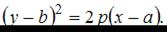Тогда уравнением параболы, изображенной на чертеже, является …

1.

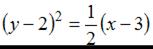
2.

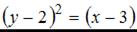
3.

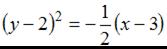
4.

 

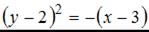
ЗАДАНИЕ N 2
Тема: Кривые второго порядк

Известно, что уравнение параболы имеет вид 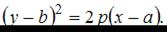Тогда уравнением параболы, изображенной на чертеже, является …

1.

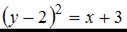
2.

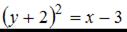
3.

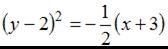
4.

 

 

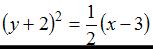
 ЗАДАНИЕ N 3
Тема: Кривые второго порядка
Уравнением окружности, изображенной на чертеже,
является …1.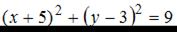

                 2.

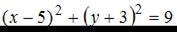
                  3.

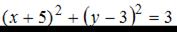
              \4.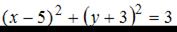

 

 

ЗАДАНИЕ N 4
Тема: Кривые второго порядка
Уравнением эллипса, изображенного на чертеже,

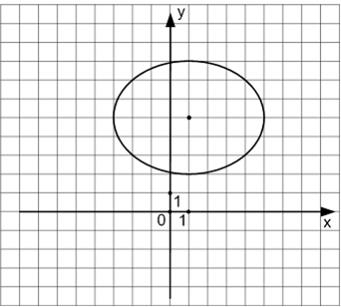
является …

 

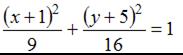
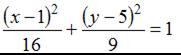
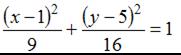
ЗАДАНИЕ N 5
Тема: Кривые второго порядка
Известно, что уравнение параболы имеет вид 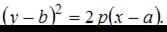Тогда уравнением параболы, изображенной на чертеже,

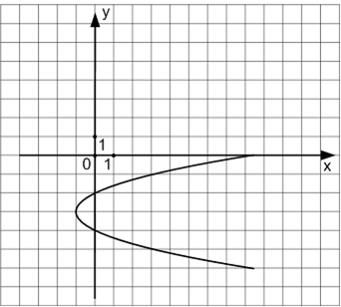
является …

 

 

РАЗДЕЛ 3