ТЕМА 4 КООРДИНАТЫ ТОЧЕК НА ПЛОСКОСТИ И В ПРОСТРАНСТВЕ
КОНСПЕКТ 4
4.1 СИСТЕМА КООРДИНАТ В ПРОСТРАНСТВЕ
Теперь рассмотрим точки в трехмерном пространстве, здесь практически всё так же, КАК НА ПЛОСКОСТИ! Только добавится ещё одна координата. Трехмерные чертежи выполнять тяжко, поэтому ограничимся одним рисунком.
 |

|
|



 | |||
| |||
Перед вами Декартова система координат трехмерного пространства, ее называют чаще прямоугольная система координат, координатные оси попарно ортогональны: и. Ось 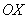 наклонена под углом 45 градусов только для того, чтобы складывалось визуальное впечатление пространства.
наклонена под углом 45 градусов только для того, чтобы складывалось визуальное впечатление пространства.
ПРАКТИКУМ 4
ЗАДАНИЕ N 1
Тема: Координаты точек на плоскости и в пространстве
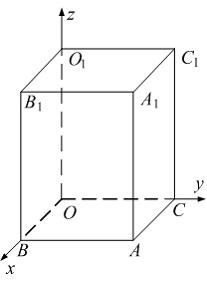
Дан прямоугольный параллелепипед.
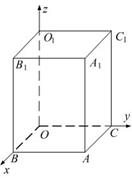
Одна из его вершин совпадает с началом координат.
Ребра, исходящие из этой вершины, лежат на осях координат.
Известно, что 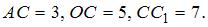
Найти координаты точек: . 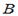 ,
, 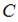 ,
, 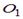 ,
, 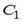
Решение:
Так как 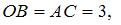
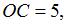 и
и 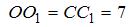 то
то 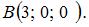
Аналогично можно найти, что 
ЗАДАНИЕ N 2
Тема: Координаты точек на плоскости и в пространстве
Дан прямоугольный параллелепипед.
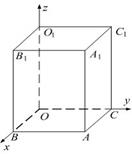
Одна из его вершин совпадает с началом координат.
Ребра, исходящие из этой вершины, лежат на осях координат.
Известно, что 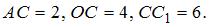
Найти координаты точек: А, B,C, 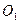 .
.
Решение:
Так как 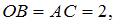
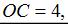 и
и 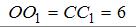 то
то 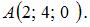
Аналогично можно найти, что 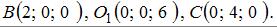
ЗАДАНИЕ N 3
Тема: Координаты точек на плоскости и в пространстве
Ребро куба 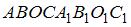 равно 26.
равно 26.
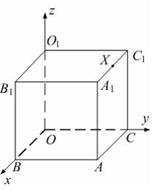
Вершина куба O совпадает с началом координат. Ребра, исходящие из этой вершины, лежат на осях координат, как изображено на рисунке. X − середина ребра 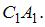 Установите соответствие между точками данного куба и их координатами. Найти координаты точек:
Установите соответствие между точками данного куба и их координатами. Найти координаты точек:

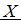
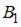
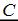
Решение:
Если точка 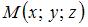 лежит на координатной плоскости или на оси координат, то некоторые ее координаты равны нулю. Так, если
лежит на координатной плоскости или на оси координат, то некоторые ее координаты равны нулю. Так, если 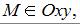 то
то 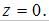 Аналогично, если
Аналогично, если 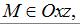 то
то 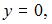 а если
а если 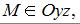 то
то 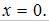 Если
Если 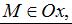 то
то 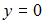 и
и 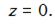 Аналогично, если
Аналогично, если 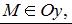 то
то 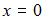 и
и 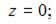 и если
и если 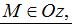 то
то 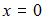 и
и 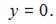 Учитывая, что длина ребра куба равна 26, имеем:
Учитывая, что длина ребра куба равна 26, имеем: 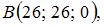
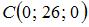 и
и 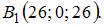 Точка X лежит на верхней грани куба и, значит, координата
Точка X лежит на верхней грани куба и, значит, координата 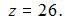 Так как X − середина ребра
Так как X − середина ребра 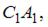 то
то 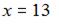 и
и 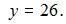 Получили:
Получили: 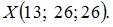
САМОСТОЯТЕЛЬНАЯ РАБОТА 4
ЗАДАНИЕ N 1
Тема: Координаты точек на плоскости и в пространстве
Дан прямоугольный параллелепипед.
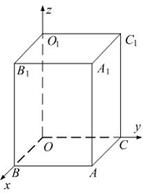
Одна из его вершин совпадает с началом координат.
Ребра, исходящие из этой вершины, лежат на осях координат.
Известно, что 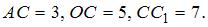
Установите соответствие между вершинами данного параллелепипеда и их координатами.
1. 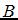
2. 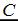
3. 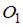
4. 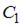
1 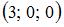
2 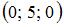
3 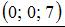
4 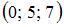
5 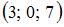
ЗАДАНИЕ N 2
Тема: Координаты точек на плоскости и в пространстве
Дан прямоугольный параллелепипед.
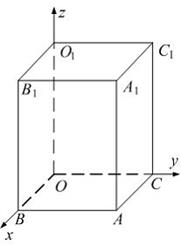
Одна из его вершин совпадает с началом координат.
Ребра, исходящие из этой вершины, лежат на осях координат.
Известно, что 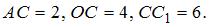
Установите соответствие между вершинами данного параллелепипеда и их координатами.
1. 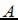
2. 
3. 
4. 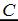
1. 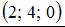
2. 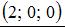
3. 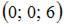
4. 
5. 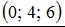
ЗАДАНИЕ N 3
Тема: Координаты точек на плоскости и в пространстве
Ребро куба 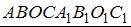 равно 26.
равно 26.
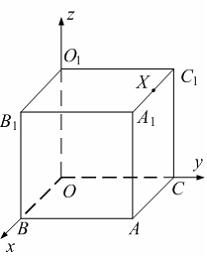
Вершина куба O совпадает с началом координат. Ребра, исходящие из этой вершины, лежат на осях координат, как изображено на рисунке. X − середина ребра 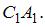 Установите соответствие между точками данного куба и их координатами.
Установите соответствие между точками данного куба и их координатами.
1. 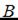
2. 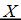
3. 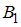
4. 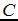
1. 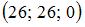
2. 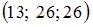
3. 
4. 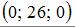
5. 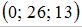
Дата: 2019-07-31, просмотров: 613.