КОНСПЕКТ 9
ПОРЯДОК НАХОЖДЕНИЯ ЭКСТРЕМУМОВ ФУНКЦИИ
1. Найти область определения функции и интервалы, на которых функция непрерывна.
2. Найти производную функции f '(x).
3. Найти критические точки функции y = f (x), т.е. точки, принадлежащие области определения функции, в которых производная f '(x) обращается в нуль или не существует.
4. Исследовать характер изменения функции f (x) и знак производной f '(x) в промежутках, на которые найденные критические точки делят область определения функции y = f (x).
5. Относительно каждой критической точки определить, является ли она точкой максимума, минимума или не является точкой экстремума.
Помни: критическая точка x0 есть точка минимума, если она отделяет промежуток, в котором f '(x)<0, от промежутка, в котором f '(x)>0, и точка максимума - в противном случае. Если же в соседних промежутках, разделенных критической точкой x0, знак производной не меняется, то в точке x0 функция экстремума не имеет.
Пример 1
Исследовать на экстремум функцию f(x) = x3–3x2
Решение:
1) Функция определена для всех 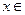 R. Найдем производную: f '(x)=3x2–6x.
R. Найдем производную: f '(x)=3x2–6x.
2) Из уравнения 3x2–6x = 3x(x–2) = 0 получим критические точки функции x1=0 и x2=2.
3) Так как при переходе через точку x1=0 производная меняет знак с плюса на минус, то в этой точке функция имеет максимум.
4) При переходе через точку x2 =2 производная меняет знак с минуса на плюс, поэтому в точке x2 = 2 у функции минимум.
| x | ( 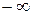 ;0] ;0]
| 0 | [0; 2] | 2 | [2; + 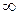 ) )
|
| f '(x) | + | 0 | – | 0 | + |
| f (x) | ↑ | fmax(0) = 0 | ↓ | fmin(2) = – 4 | ↑ |
Ответ: (0; 0) – точка максимума, (2; -4) – точка минимума;
9.2 ПОРЯДОК НАХОЖДЕНИЯ НАИБОЛЬШЕГО И НАИМЕНЬШЕГО ЗНАЧЕНИЙ ФУНКЦИИ НА ОТРЕЗКЕ
- Найти все критические точки, принадлежащие промежутку [ a,b ], и вычислить значения функции в этих точках.
- Вычислить значения функции на концах отрезка [ a,b ],т.е.найти f(a) и f(b).
- сравнить полученные результаты; наибольшее из найденных значений является наибольшим значением функции на отрезке [ a,b ]; аналогично, наименьшее из найденных значений есть наименьшее значение функции на этом отрезке.
ПРАКТИКУМ 9
ЗАДАНИЕ N 1
Тема: Экстремум функции
Для функции 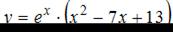 точка максимума
точка максимума  принимает значение, равное …
принимает значение, равное …
Решение:
Для отыскания точек экстремума найдем точки, в которых производная равна нулю или не существует.
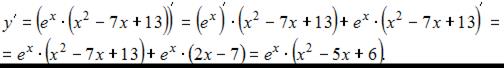
Заметим, что производная существует для любого значения х, приравняем ее к нулю, получим: 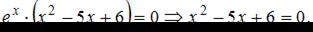
Последнее уравнение имеет корни: 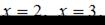 Отметим найденные значения на числовой прямой. Найдем знак производной
Отметим найденные значения на числовой прямой. Найдем знак производной 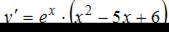 на каждом из получившихся промежутков.
на каждом из получившихся промежутков.

Точки  и
и  являются экстремальными, так как при переходе через эти точки производная меняет знак.
являются экстремальными, так как при переходе через эти точки производная меняет знак.
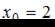 – точка максимума, так как производная меняет знак с «+» на «–».
– точка максимума, так как производная меняет знак с «+» на «–».
ЗАДАНИЕ N 2
Тема: Экстремум функции
Для функции 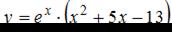 точка минимума
точка минимума  принимает значение, равное …
принимает значение, равное …
Решение:
Для отыскания точек экстремума найдем точки, в которых производная равна нулю или не существует.
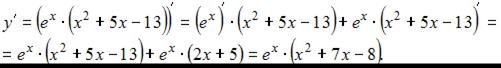
Заметим, что производная существует для любого значения х, приравняем ее к нулю, получим: 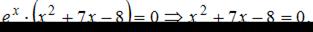
Последнее уравнение имеет корни:  Отметим найденные значения на числовой прямой. Найдем знак производной
Отметим найденные значения на числовой прямой. Найдем знак производной 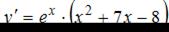 на каждом из получившихся промежутков.
на каждом из получившихся промежутков.

Точки  и
и  являются экстремальными, так как при переходе через эти точки производная меняет знак.
являются экстремальными, так как при переходе через эти точки производная меняет знак.
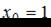 – точка минимума, так как производная меняет знак с «−» на «+».
– точка минимума, так как производная меняет знак с «−» на «+».
ЗАДАНИЕ N 3
Тема: Экстремум функции
Для функции  точка минимума
точка минимума  принимает значение, равное …
принимает значение, равное …
Решение:
Для отыскания точек экстремума найдем точки, в которых производная равна нулю или не существует. 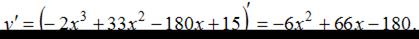
Заметим, что производная существует для любого значения х, приравняем ее к нулю, получим: 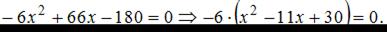
Последнее уравнение имеет корни:  Отметим найденные значения на числовой прямой. Найдем знак производной
Отметим найденные значения на числовой прямой. Найдем знак производной 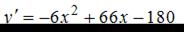 на каждом из получившихся промежутков.
на каждом из получившихся промежутков.

Точки  и
и  являются экстремальными, так как при переходе через эти точки производная меняет знак.
являются экстремальными, так как при переходе через эти точки производная меняет знак. 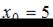 – точка минимума, так как производная меняет знак с «−» на «+».
– точка минимума, так как производная меняет знак с «−» на «+».
ЗАДАНИЕ N 4
Тема: Экстремум функции
Для функции 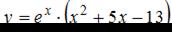 точка минимума
точка минимума  принимает значение, равное …
принимает значение, равное …
Решение:
Для отыскания точек экстремума найдем точки, в которых производная равна нулю или не существует.
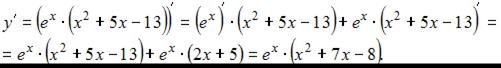
Заметим, что производная существует для любого значения х, приравняем ее к нулю, получим: 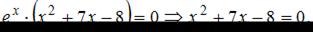
Последнее уравнение имеет корни:  Отметим найденные значения на числовой прямой. Найдем знак производной
Отметим найденные значения на числовой прямой. Найдем знак производной 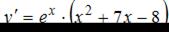 на каждом из получившихся промежутков.
на каждом из получившихся промежутков.

Точки  и
и  являются экстремальными, так как при переходе через эти точки производная меняет знак.
являются экстремальными, так как при переходе через эти точки производная меняет знак.
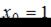 – точка минимума, так как производная меняет знак с «−» на «+».
– точка минимума, так как производная меняет знак с «−» на «+».
ЗАДАНИЕ N 5
Тема: Экстремум функции
Для функции 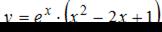 точка минимума
точка минимума  принимает значение, равное …
принимает значение, равное …
Решение:
Для отыскания точек экстремума найдем точки, в которых производная равна нулю или не существует.
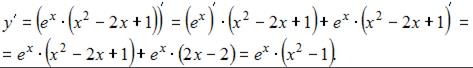
Заметим, что производная существует для любого значения х, приравняем ее к нулю, получим: 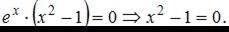
Последнее уравнение имеет корни: 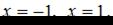 Отметим найденные значения на числовой прямой. Найдем знак производной
Отметим найденные значения на числовой прямой. Найдем знак производной 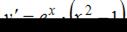 на каждом из получившихся промежутков.
на каждом из получившихся промежутков.

Точки  и
и  являются экстремальными, так как при переходе через эти точки производная меняет знак.
являются экстремальными, так как при переходе через эти точки производная меняет знак.
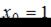 – точка минимума, так как производная меняет знак с «−» на «+».
– точка минимума, так как производная меняет знак с «−» на «+».
ЗАДАНИЕ N 6
Тема: Наибольшее и наименьшее значения функции
Наибольшее значение функции 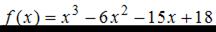 на отрезке
на отрезке 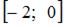
равно …
Решение:
Заметим, что функция 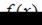 непрерывна на отрезке
непрерывна на отрезке 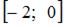 . Найдем значения функции на концах отрезка:
. Найдем значения функции на концах отрезка:
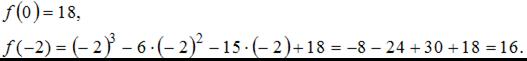
Найдем производную данной функции: 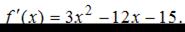
Тогда 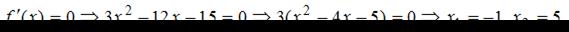
Так как 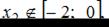 то нужно найти только
то нужно найти только 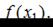
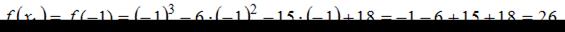
Сравнивая значения  и
и 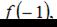 определим, что наибольшее значение функции равно 26.
определим, что наибольшее значение функции равно 26.
ЗАДАНИЕ N 7
Тема: Наибольшее и наименьшее значения функции
Наибольшее значение функции 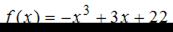 на отрезке
на отрезке 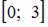 равно …
равно …
Решение:
Заметим, что функция 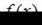 непрерывна на отрезке
непрерывна на отрезке 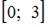 . Найдем значения функции на концах отрезка:
. Найдем значения функции на концах отрезка:
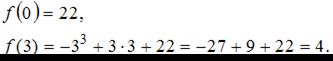
Найдем производную данной функции: 
Тогда 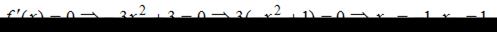
Так как 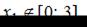 то нужно найти только
то нужно найти только 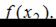
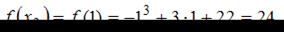
Сравнивая значения  и
и 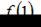 определим, что наибольшее значение функции равно 24.
определим, что наибольшее значение функции равно 24.
ЗАДАНИЕ N 8
Тема: Наибольшее и наименьшее значения функции
Наименьшее значение функции 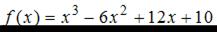 на отрезке
на отрезке 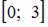 равно …
равно …
Решение:
Заметим, что функция 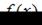 непрерывна на отрезке
непрерывна на отрезке 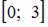 . Найдем значения функции на концах отрезка:
. Найдем значения функции на концах отрезка:
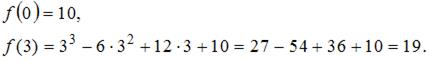
Найдем производную данной функции: 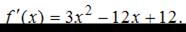
Тогда 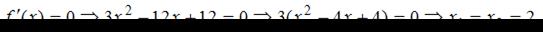
Так как найденные значения х принадлежат отрезку 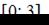 то нужно найти
то нужно найти 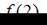
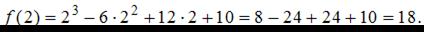
Сравнивая значения  и
и 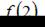 определим, что наименьшее значение функции равно 10.
определим, что наименьшее значение функции равно 10.
ЗАДАНИЕ N 9
Тема: Наибольшее и наименьшее значения функции
Наименьшее значение функции 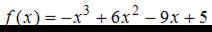 на отрезке
на отрезке 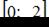 равно …
равно …
Решение:
Заметим, что функция 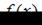 непрерывна на отрезке
непрерывна на отрезке 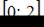 .
.
Найдем значения функции на концах отрезка:
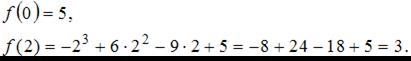
Найдем производную данной функции.
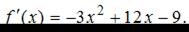
Тогда 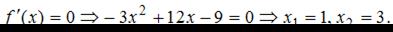
Так как 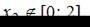 то нужно найти только
то нужно найти только 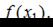
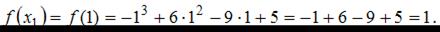
Сравнивая значения  и
и 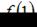 , определим, что наименьшее значение функции равно 1.
, определим, что наименьшее значение функции равно 1.
ЗАДАНИЕ N 10
Тема: Наибольшее и наименьшее значения функции
Наибольшее значение функции 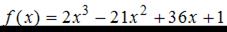 на отрезке
на отрезке 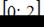 равно …
равно …
Решение:
Заметим, что функция 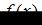 непрерывна на отрезке
непрерывна на отрезке 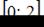 . Найдем значения функции на концах отрезка:
. Найдем значения функции на концах отрезка:
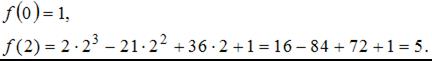
Найдем производную данной функции: 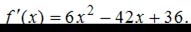
Тогда 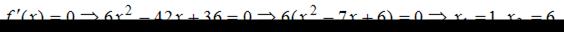
Так как 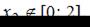 то нужно найти только
то нужно найти только 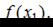
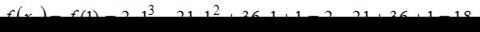
Сравнивая значения  и
и 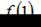 определим, что наибольшее значение функции равно 18.
определим, что наибольшее значение функции равно 18.
ЗАДАНИЕ N 11
Тема: Наибольшее и наименьшее значения функции
Наибольшее значение функции 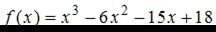 на отрезке
на отрезке 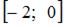
равно …
Решение:
Заметим, что функция 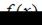 непрерывна на отрезке
непрерывна на отрезке 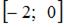 . Найдем значения функции на концах отрезка:
. Найдем значения функции на концах отрезка:
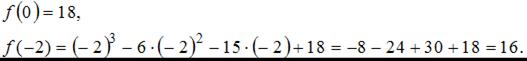
Найдем производную данной функции: 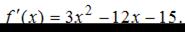
Тогда 
Так как 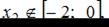 то нужно найти только
то нужно найти только 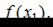
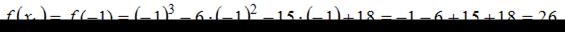
Сравнивая значения  и
и 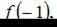 определим, что наибольшее значение функции равно 26.
определим, что наибольшее значение функции равно 26.
САМОСТОЯТЕЛЬНАЯ РАБОТА 9
ЗАДАНИЕ N 1
Тема: Экстремум функции
Для функции 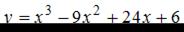 точка минимума
точка минимума  принимает значение, равное …
принимает значение, равное …
ЗАДАНИЕ N 2
Тема: Экстремум функции
Для функции 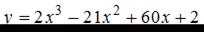 точка минимума
точка минимума  принимает значение, равное …
принимает значение, равное …
ЗАДАНИЕ N 3
Тема: Экстремум функции
Для функции 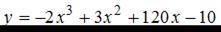 точка максимума
точка максимума  принимает значение, равное …
принимает значение, равное …
ЗАДАНИЕ N 4
Тема: Экстремум функции
Для функции 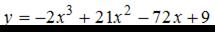 точка минимума
точка минимума  принимает значение, равное …
принимает значение, равное …
ЗАДАНИЕ N 5
Тема: Экстремум функции
Для функции 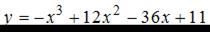 точка максимума
точка максимума  принимает значение, равное …
принимает значение, равное …
ЗАДАНИЕ N 6
Тема: Экстремум функции
Для функции 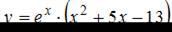 точка минимума
точка минимума  принимает значение, равное …
принимает значение, равное …
ЗАДАНИЕ N 7
Тема: Экстремум функции
Для функции 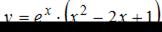 точка минимума
точка минимума  принимает значение, равное …
принимает значение, равное …
ЗАДАНИЕ N 8
Тема: Наибольшее и наименьшее значения функции
Наибольшее значение функции 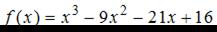 на отрезке
на отрезке 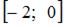
равно …
ЗАДАНИЕ N 9
Тема: Наибольшее и наименьшее значения функции
Наименьшее значение функции 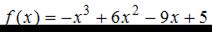 на отрезке
на отрезке 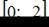 равно …
равно …
ЗАДАНИЕ N 10
Тема: Наибольшее и наименьшее значения функции
Наименьшее значение функции 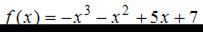 на отрезке
на отрезке 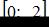
равно …
ТЕМА 10 ДИФФЕРЕНЦИАЛ ФУНКЦИИ
КОНСПЕКТ 10
Дата: 2019-07-31, просмотров: 300.