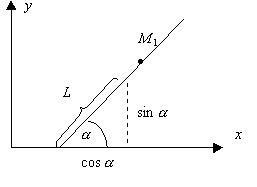
Рассмотрим снова прямую L. Ее положение вполне определяется заданием угла a (Ox, L) и точки М(х ,у ), лежащей на этой прямой.
В качестве направляющего вектора возьмем единичный вектор
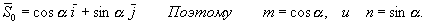
Проверим, будет ли этот вектор единичным?
Его длина 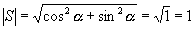
Тогда каноническое уравнение прямой будет иметь вид:
 ,
,
получим у-у1 = k(х – х1) – это прежнее уравнение прямой с угловым коэффициентом.
Уравнение прямой, проходящей через две данные точки.
Пусть на плоскости даны М1(х1у1) и М2(х2у2). Составим каноническое уравнение прямой, проходящей через эти две точки в качестве направляющего вектора S возьмем M1M2
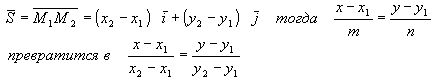
это уравнение прямой, проходящей через две данные точки (х1 у1) и (х2, у2)
ПРАКТИКУМ 6
ЗАДАНИЕ N 1
Тема: Линии и их уравнения на плоскости
В координатной плоскости XOY линия задана параметрически:
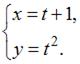
Тогда этой линии принадлежат точки … 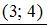
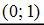
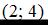
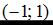
Решение:
Используя одну из координат точки, найдем значение t и, подставив его в другое уравнение, получим вторую координату точки.
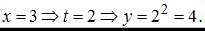 Точка с координатами
Точка с координатами 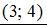 принадлежит данной линии.
принадлежит данной линии.
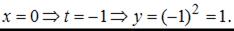 Точка с координатами
Точка с координатами 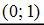 принадлежит данной линии.
принадлежит данной линии.
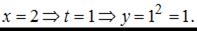 Точка с координатами
Точка с координатами 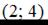 не принадлежит данной линии.
не принадлежит данной линии.
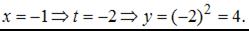 Точка с координатами
Точка с координатами 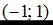 не принадлежит данной линии.
не принадлежит данной линии.
ЗАДАНИЕ N 2
Тема: Линии и их уравнения на плоскости
В координатной плоскости XOY линия задана параметрически:
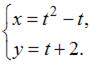
Тогда этой линии принадлежат точки … 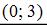 ,
, 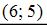 ,
, 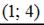 ,
, 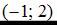
Решение:
Используя одну из координат точки, найдем значение t и, подставив его в другое уравнение, получим вторую координату точки.
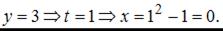 Точка с координатами
Точка с координатами 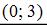 принадлежит данной линии.
принадлежит данной линии.
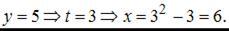 Точка с координатами
Точка с координатами 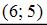 принадлежит данной линии.
принадлежит данной линии.
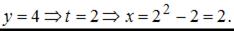 Точка с координатами
Точка с координатами 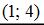 не принадлежит данной линии.
не принадлежит данной линии.
 Точка с координатами
Точка с координатами 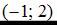 не принадлежит данной линии.
не принадлежит данной линии.
ЗАДАНИЕ N 3
Тема: Линии и их уравнения на плоскости
В координатной плоскости XOY линия задана параметрически:
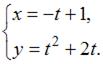
Тогда этой линии принадлежат точки …  ,
, 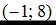 ,
, 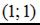 ,
, 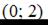
Решение:
Используя одну из координат точки, найдем значение t и, подставив его в другое уравнение, получим вторую координату точки.
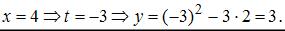 Точка с координатами
Точка с координатами  принадлежит данной линии.
принадлежит данной линии.
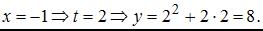 Точка с координатами
Точка с координатами 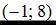 принадлежит данной линии.
принадлежит данной линии.
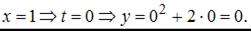 Точка с координатами
Точка с координатами 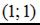 не принадлежит данной линии.
не принадлежит данной линии.
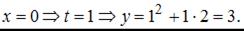 Точка с координатами
Точка с координатами 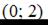 не принадлежит данной линии.
не принадлежит данной линии.
ЗАДАНИЕ N 4
Тема: Линии и их уравнения на плоскости
В координатной плоскости XOY линия задана уравнением 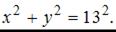
Тогда эта линия проходит через точки … 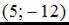 ,
, 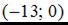 ,
, 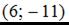 ,
, 
Решение:
Нужно подставить координаты данных точек в уравнение линии. Если получится тождество, то линия проходит через точку. В противном случае − нет.
1.  .
. 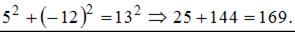 Точка с координатами
Точка с координатами 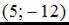 принадлежит линии.
принадлежит линии.
2. 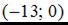 .
. 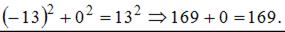 Точка с координатами
Точка с координатами 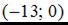 принадлежит линии.
принадлежит линии.
1. 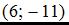 .
. 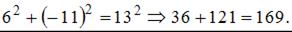 Точка с координатами
Точка с координатами 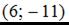 не принадлежит линии.
не принадлежит линии.
4.  .
. 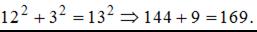 Точка с координатами
Точка с координатами 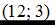 не принадлежит линии.
не принадлежит линии.
ЗАДАНИЕ N 5
Тема: Уравнение прямой на плоскости
Известно, что уравнение прямой, проходящей через две точки A и B, имеет вид
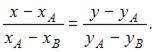 Тогда для точек
Тогда для точек 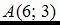 и
и 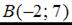 уравнение прямой может быть записано в виде …
уравнение прямой может быть записано в виде …
Решение:
Воспользуемся формулой: 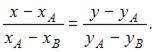 Имеем:
Имеем: 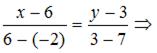
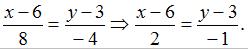 Проделав элементарные преобразования, получим
Проделав элементарные преобразования, получим 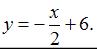
ЗАДАНИЕ N 6
Тема: Уравнение прямой на плоскости
Известно, что уравнение прямой, проходящей через две точки A и B, может быть получено по формуле 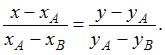
Тогда для точек 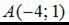 и
и 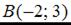 уравнением прямой является …
уравнением прямой является …
Решение:
Воспользуемся формулой 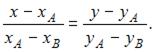
Имеем: 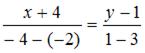 или
или 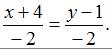
Проделав элементарные преобразования, получим 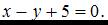
ЗАДАНИЕ N 7
Тема: Уравнение прямой на плоскости
Известно, что уравнение прямой, проходящей через две точки A и B, может быть получено по формуле 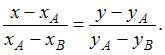
Тогда для точек 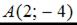 и
и 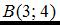 уравнением прямой является …
уравнением прямой является …
Решение:
Воспользуемся формулой 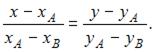
Имеем: 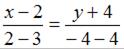 или
или 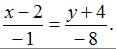
Проделав элементарные преобразования, получим 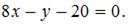
ЗАДАНИЕ N 8
Тема: Уравнение прямой на плоскости
Известно, что уравнение прямой, проходящей через две точки A и B, имеет вид 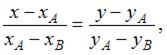 тогда для точек
тогда для точек 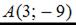 и
и 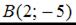 уравнение прямой может быть записано в виде …
уравнение прямой может быть записано в виде …
Решение:
Воспользуемся формулой: 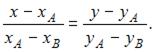 Имеем:
Имеем: 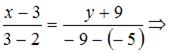
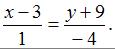 Проделав элементарные преобразования, получим
Проделав элементарные преобразования, получим 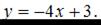
САМОСТОЯТЕЛЬНАЯ РАБОТА 6
ЗАДАНИЕ N 1
Тема: Линии и их уравнения на плоскости
В координатной плоскости XOY линия задана параметрически:
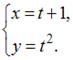
Какие из указанных точек принадлежат этой линии?
1. 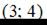
2. 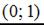
3. 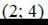
4. 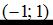
ЗАДАНИЕ N 2
Тема: Линии и их уравнения на плоскости
В координатной плоскости XOY линия задана параметрически:
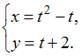
Какие из указанных точек принадлежат этой линии?
1. 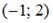
2. 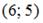
3. 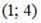
4. 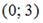
ЗАДАНИЕ N 3
Тема: Линии и их уравнения на плоскости
В координатной плоскости XOY линия задана параметрически:
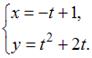
Какие из указанных точек принадлежат этой линии?
1. 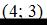
2. 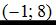
3. 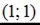
4. 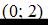
ЗАДАНИЕ N 4
Тема: Линии и их уравнения на плоскости
В координатной плоскости XOY линия задана уравнением 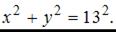
Тогда эта линия проходит через точки …
1. 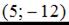
2. 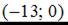
3. 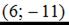
4. 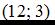
ЗАДАНИЕ N 5
Тема: Уравнение прямой на плоскости
Известно, что уравнение прямой, проходящей через две точки A и B, имеет вид
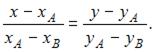 Тогда для точек
Тогда для точек 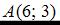 и
и 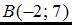 уравнение прямой может быть записано в виде …
уравнение прямой может быть записано в виде …
1. 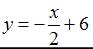
2. 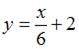
3. 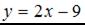
4. 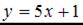
ЗАДАНИЕ N 6
Тема: Уравнение прямой на плоскости
Известно, что уравнение прямой, проходящей через две точки A и B, может быть получено по формуле 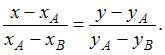
Тогда для точек 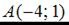 и
и 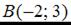 уравнением прямой является …
уравнением прямой является …
1. 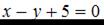
2. 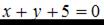
3. 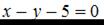
4. 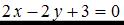
ЗАДАНИЕ N 7
Тема: Уравнение прямой на плоскости
Известно, что уравнение прямой, проходящей через две точки A и B, может быть получено по формуле 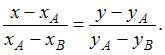
Тогда для точек 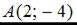 и
и 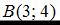 уравнением прямой является …
уравнением прямой является …
1. 
2. 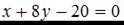
3. 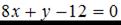
4. 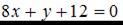
Дата: 2019-07-31, просмотров: 379.