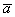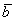Сначала про угол между векторами. Думаю, всем интуитивно понятно, что такое угол между векторами, но на всякий случай чуть подробнее. Рассмотрим свободные ненулевые векторы и . Если отложить данные векторы от произвольной точки 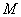, то получится картинка, которую многие уже представили мысленно:

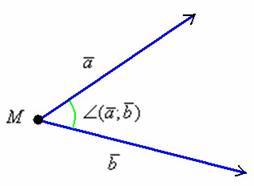
Угол между векторами 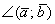может принимать значения от 0 до 180 градусов (от 0 до 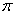радиан) включительно. Аналитически данный факт записывается в виде двойного неравенства: 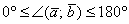либо 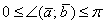(в радианах).

В литературе значок угла 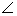часто пропускают и пишут просто .

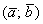Определение: Скалярным произведением двух векторов 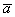и 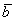называется ЧИСЛО, равное произведению длин этих векторов на косинус угла между ними:

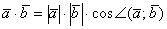
Вот это вот уже вполне строгое определение.

Акцентируем внимание на существенной информации:

Обозначение: скалярное произведение обозначается через 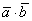или просто .

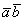Результат операции является ЧИСЛОМ: Умножается вектор на вектор, а получается число. Действительно, если длины векторов 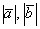– это числа, косинус угла – число, то их произведение 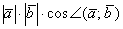тоже будет числом.

Как уже отмечалось, угол между векторами может изменяться в пределах 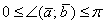, и при этом возможны следующие случаи:

1) Если угол между векторами острый: 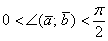(от 0 до 90 градусов), то 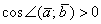, и скалярное произведение будет положительным: 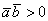. Особый случай: если векторы сонаправлены, то угол между ними считается нулевым 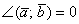, и скалярное произведение также будет положительным. Поскольку 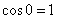, то формула упрощается: .

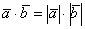2) Если угол между векторами тупой: 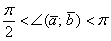(от 90 до 180 градусов), то 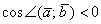, и, соответственно, скалярное произведение отрицательно: 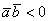. Особый случай: если векторы направлены противоположно, то угол между ними считается развёрнутым: 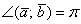(180 градусов). Скалярное произведение тоже отрицательно, так как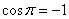

Справедливы и обратные утверждения:

1) Если 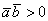, то угол между данными векторами острый. Как вариант, векторы сонаправлены.

2) Если 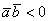, то угол между данными векторами тупой. Как вариант, векторы направлены противоположно.

Но особый интерес представляет третий случай:

3) Если угол между векторами прямой: 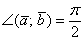(90 градусов), то 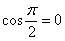и скалярное произведение равно нулю: 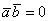. Обратное тоже верно: если 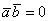, то 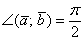. Компактно утверждение формулируется так: Скалярное произведение двух векторов равно нулю тогда и только тогда, когда данные векторы ортогональны. Короткая математическая запись: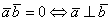

Третий случай имеет большую практическую значимость, поскольку позволяет проверить, ортогональны векторы или нет. Речь идёт о длине, не забываем указать размерность – «единицы».