КОНСПЕКТ 8

Наша задача научиться находить производные. Очень хорошая новость состоит в том, что научиться брать производные не так сложно, существует довольно чёткий алгоритм решения (и объяснения) этого задания.

Пример 1

Найти производную функции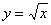

Решение: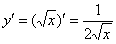

Это простейший пример, пожалуйста, найдите его в таблице производных элементарных функций. Теперь посмотрим на решение и проанализируем, что же произошло? А произошла следующая вещь: у нас была функция 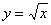, которая в результате решения превратилась в функцию .

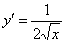Говоря совсем просто, для того чтобы найти производную функции, нужно по определенным правилам превратить её в другую функцию. Посмотрите еще раз на таблицу производных – там функции превращаются в другие функции. Единственным исключением является экспоненциальная функция 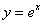, которая превращается сама в себя. Операция нахождения производной называется дифференцированием.

Обозначения: Производную обозначают 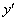или

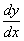
ПРАВИЛА ДИИФЕРЕНЦИРОВАНИЯ

Постоянное число можно (и нужно) вынести за знак производной

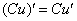, где 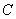– постоянное число (константа)

Пример 2

Найти производную функции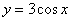

Смотрим в таблицу производных. Производная косинуса там есть, но у нас .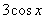

Решаем:

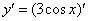
Самое время использовать правило, выносим постоянный множитель за знак производной:

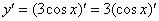
А теперь превращаем наш косинус по таблице:

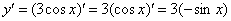
Ну и результат желательно немного «причесать» – ставим минус на первое место, заодно избавляясь от скобок:

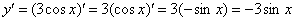
Готово.

Производная суммы равна сумме производных

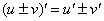
Пример 3

Найти производную функции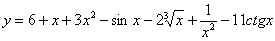

Решаем.

Обычно в ходе решения первые два правила применяют одновременно (чтобы не переписывать лишний раз длинное выражение).

Все функции, находящиеся под штрихами, являются элементарными табличными функциями, с помощью таблицы осуществляем превращение:

Можно всё оставить в таком виде, так как штрихов больше нет, и производная найдена. Тем не менее, подобные выражения обычно упрощают:

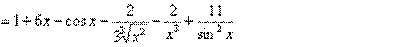
Все степени вида 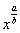желательно снова представить в виде корней, степени с отрицательными показателями – сбросить в знаменатель. Хотя этого можно и не делать, ошибкой не будет.

Производная произведения функций

Вроде бы по аналогии напрашивается формула 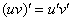…., но неожиданность состоит в том, что:

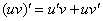
Я не буду объяснять, почему именно так, наша задача научиться решать производные, а не разбираться в теории.

Пример 4

Найти производную функции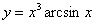

Здесь у нас произведение двух функций, зависящих от .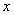
Сначала применяем наше странное правило, а затем превращаем функции по таблице производных:

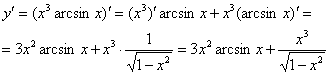
Сложно? Вовсе нет, вполне доступно даже для чайника.