Скалярное произведение векторов 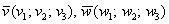 , заданных в ортонормированном базисе
, заданных в ортонормированном базисе 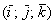 , выражается формулой
, выражается формулой 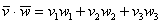
То есть, скалярное произведение равно сумме произведений соответствующих координат векторов.
Пример 2
Найти скалярное произведение векторов:
а) 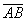 и
и 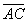 , если даны точки
, если даны точки 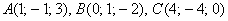
Решение:
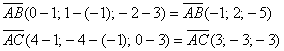
Надеюсь, эта простейшая задача у вас уже отработана.
По формуле 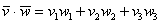 вычислим скалярное произведение:
вычислим скалярное произведение:
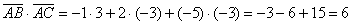
К слову: скалярное произведение положительно, значит, угол между пространственными векторами 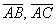 является острым.
является острым.
Проверка векторов на ортогональность с помощью скалярного произведения
Вернёмся к важному случаю, когда векторы являются ортогональными. Напоминаю: векторы 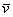 и
и 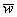 ортогональны тогда и только тогда, когда
ортогональны тогда и только тогда, когда 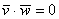 . В координатах данный факт запишется следующим образом:
. В координатах данный факт запишется следующим образом:
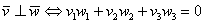
Пример 3
а) Проверить ортогональность векторов: 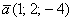 и
и 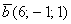
Решение:
а) Выясним, будут ли ортогональны пространственные векторы. Вычислим их скалярное произведение:
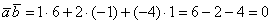 , следовательно,
, следовательно, 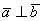
Обратите внимание на два существенных момента:
– В данном случае нас не интересует конкретное значение скалярного произведения, важно, что оно не равно нулю.
Ответ: а) 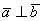 ,
,
Пример 4
При каком значении 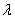 векторы
векторы 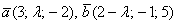 будут ортогональны?
будут ортогональны?
Решение: По условию требуется найти такое значение параметра 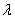 , чтобы данные векторы были ортогональны. Два вектора пространства
, чтобы данные векторы были ортогональны. Два вектора пространства 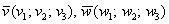 ортогональны тогда и только тогда, когда
ортогональны тогда и только тогда, когда 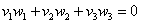 .
.
Дело за малым, составим уравнение:
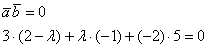
Раскрываем скобки и приводим подобные слагаемые:
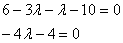
Решаем простейшее линейное уравнение:
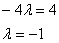
Ответ: при 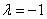
В рассмотренной задаче легко выполнить проверку, в исходные векторы 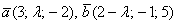 подставляем полученное значение параметра
подставляем полученное значение параметра 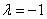 :
:
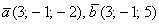
И находим скалярное произведение:
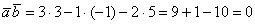 – да, действительно, при
– да, действительно, при 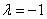 векторы
векторы 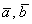 ортогональны, что и требовалось проверить.
ортогональны, что и требовалось проверить.
ПРАКТИКУМ 5
ЗАДАНИЕ N 1
Тема: Линейные операции над векторами
Даны векторы 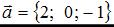 и
и 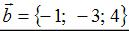 .
.
Тогда сумма координат вектора 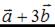 равна …
равна …
Решение:
Напоминаем, что каждая координата произведения вектора на число
равна произведению соответствующей координаты вектора на это число.
Значит, имеем 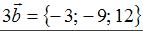 .
.
Каждая координата суммы двух векторов равна сумме соответствующих координат этих векторов.
Тогда вектор 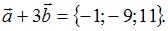 Сумма координат полученного вектора равна
Сумма координат полученного вектора равна 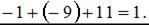
ЗАДАНИЕ N 2
Тема: Линейные операции над векторами
Даны векторы 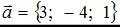 и
и 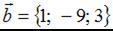 . Тогда сумма координат вектора
. Тогда сумма координат вектора 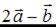 равна …
равна …
Решение:
Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число. Значит, имеем 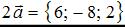 . Каждая координата суммы двух векторов равна сумме соответствующих координат этих векторов. Тогда вектор
. Каждая координата суммы двух векторов равна сумме соответствующих координат этих векторов. Тогда вектор 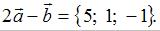 Сумма координат полученного вектора равна
Сумма координат полученного вектора равна 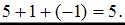
ЗАДАНИЕ N 3
Тема: Линейные операции над векторами
Даны векторы 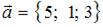 и
и 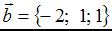 . Тогда сумма координат вектора
. Тогда сумма координат вектора 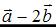 равна …
равна …
Решение:
Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число. Значит, имеем 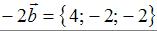 . Каждая координата суммы двух векторов равна сумме соответствующих координат этих векторов. Тогда вектор
. Каждая координата суммы двух векторов равна сумме соответствующих координат этих векторов. Тогда вектор 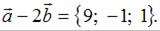 Сумма координат полученного вектора равна
Сумма координат полученного вектора равна 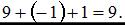
ЗАДАНИЕ N 4
Тема: Скалярное произведение векторов
Векторы заданы своими координатами: 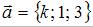 и
и 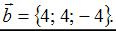
Если 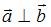 , то k равно …
, то k равно …
Решение:
Если 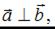 то угол между векторами равен 90○, значит, по определению
то угол между векторами равен 90○, значит, по определению 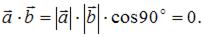 Напоминаем, что скалярное произведение векторов, заданных своими координатами
Напоминаем, что скалярное произведение векторов, заданных своими координатами 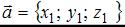 и
и 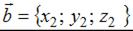 , выражается формулой:
, выражается формулой: 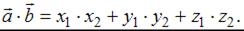 Найдем
Найдем 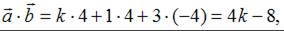 тогда
тогда 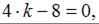 откуда
откуда 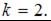
ЗАДАНИЕ N 5
Тема: Скалярное произведение векторов
Векторы заданы своими координатами: 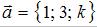 и
и 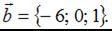
Если  , то k равно …
, то k равно …
Решение:
Если 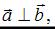 то угол между векторами равен 90○, значит, по определению
то угол между векторами равен 90○, значит, по определению 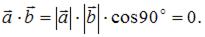 Напоминаем, что скалярное произведение векторов, заданных своими координатами
Напоминаем, что скалярное произведение векторов, заданных своими координатами 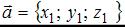 и
и 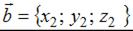 , выражается формулой:
, выражается формулой: 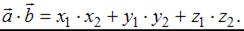 Найдем
Найдем 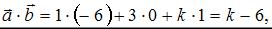 тогда
тогда 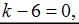 откуда
откуда 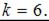
ЗАДАНИЕ N 6
Тема: Скалярное произведение векторов
Векторы заданы своими координатами: 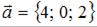 и
и 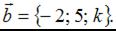
Если  , то k равно …
, то k равно …
Решение:
Если 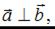 то угол между векторами равен 90○, значит, по определению
то угол между векторами равен 90○, значит, по определению 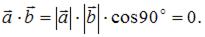 Напоминаем, что скалярное произведение векторов, заданных своими координатами
Напоминаем, что скалярное произведение векторов, заданных своими координатами 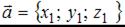 и
и 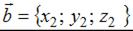 , выражается формулой:
, выражается формулой: 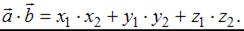 Найдем
Найдем 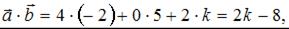 тогда
тогда 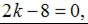 откуда
откуда 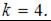
САМОСТОЯТЕЛЬНАЯ РАБОТА 5
ЗАДАНИЕ N 1
Тема: Линейные операции над векторами
Даны векторы 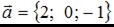 и
и 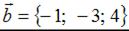 .
.
Тогда сумма координат вектора 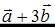 равна …
равна …
ЗАДАНИЕ N 2
Тема: Линейные операции над векторами
Даны векторы 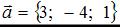 и
и 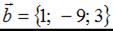 . Тогда сумма координат вектора
. Тогда сумма координат вектора 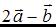 равна …
равна …
ЗАДАНИЕ N 3
Тема: Линейные операции над векторами
Даны векторы 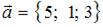 и
и 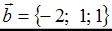 . Тогда сумма координат вектора
. Тогда сумма координат вектора 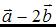 равна …
равна …
ЗАДАНИЕ N 4
Тема: Линейные операции над векторами
Даны векторы 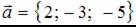 и
и 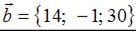 . Тогда сумма координат
. Тогда сумма координат
ЗАДАНИЕ N 5
Тема: Скалярное произведение векторов
Векторы заданы своими координатами:  и
и 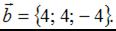
Если 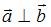 , то k равно …
, то k равно …
ЗАДАНИЕ N 6
Тема: Скалярное произведение векторов
Векторы заданы своими координатами: 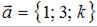 и
и 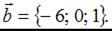
Если 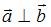 , то k равно …
, то k равно …
ЗАДАНИЕ N 7
Тема: Скалярное произведение векторов
Векторы заданы своими координатами: 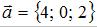 и
и 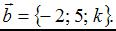
Если 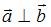 , то k равно …
, то k равно …
ЗАДАНИЕ N 8
Тема: Скалярное произведение векторов
Векторы заданы своими координатами: 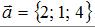 и
и 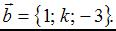
Если  , то k равно …
, то k равно …
Дата: 2019-07-31, просмотров: 292.