А вот это вот суровая действительность:
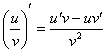
Пример 5
Найти производную функции 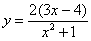
Чего здесь только нет – сумма, разность, произведение, дробь…. С чего бы начать?! Есть сомнения, нет сомнений, но, В ЛЮБОМ СЛУЧАЕ для начала рисуем скобочки и справа вверху ставим штрих:
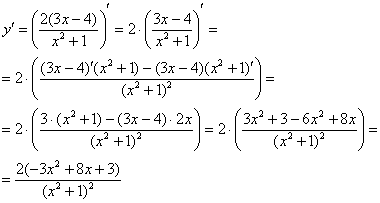
8.2 ПРОИЗВОДНАЯ СЛОЖНОЙ ФУНКЦИИ
Правило дифференцирования сложной функции:
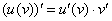
Пример 6
Найти производную функции 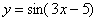
Под синусом у нас находится не просто буква «икс», а целое выражение 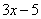 , поэтому найти производную сразу по таблице не получится. Также мы замечаем, что здесь невозможно применить первые четыре правила, вроде бы есть разность, но дело в том, что «разрывать на части» синус нельзя:
, поэтому найти производную сразу по таблице не получится. Также мы замечаем, что здесь невозможно применить первые четыре правила, вроде бы есть разность, но дело в том, что «разрывать на части» синус нельзя:
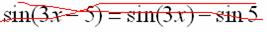
В данном примере уже из моих объяснений интуитивно понятно, что функция 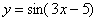 – это сложная функция, причем многочлен
– это сложная функция, причем многочлен 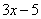 является внутренней функцией (вложением), а
является внутренней функцией (вложением), а 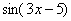 – внешней функцией.
– внешней функцией.
Первый шаг, который нужно выполнить при нахождении производной сложной функции состоит в том, чтобы разобраться, какая функция является внутренней, а какая – внешней.
В случае простых примеров вроде 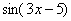 понятно, что под синус вложен многочлен
понятно, что под синус вложен многочлен 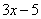 . А как же быть, если всё не очевидно? Как точно определить, какая функция является внешней, а какая внутренней? Для этого я предлагаю использовать следующий прием, который можно проводить мысленно или на черновике.
. А как же быть, если всё не очевидно? Как точно определить, какая функция является внешней, а какая внутренней? Для этого я предлагаю использовать следующий прием, который можно проводить мысленно или на черновике.
Представим, что нам нужно вычислить на калькуляторе значение выражения 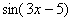 при
при 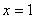 (вместо единицы может быть любое число).
(вместо единицы может быть любое число).
Что мы вычислим в первую очередь? В первую очередь нужно будет выполнить следующее действие: 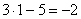 , поэтому многочлен
, поэтому многочлен 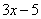 и будет внутренней функцией
и будет внутренней функцией 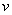 :
:
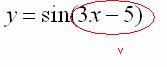
Во вторую очередь нужно будет найти 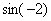 , поэтому синус – будет внешней функцией:
, поэтому синус – будет внешней функцией:
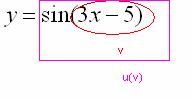
После того, как мы РАЗОБРАЛИСЬ с внутренней и внешней функциями самое время применить правило дифференцирования сложной функции 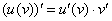 .
.
Начинаем решать. 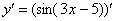
Сначала находим производную внешней функции 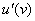 (синуса), смотрим на таблицу производных элементарных функций и замечаем, что
(синуса), смотрим на таблицу производных элементарных функций и замечаем, что 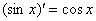 . Все табличные формулы применимы и в том, случае, если «икс» заменить сложным выражением, в данном случае:
. Все табличные формулы применимы и в том, случае, если «икс» заменить сложным выражением, в данном случае:
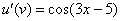
Обратите внимание, что внутренняя функция 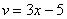 не изменилась, её мы не трогаем.
не изменилась, её мы не трогаем.
Ну и совершенно очевидно, что 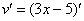
Результат применения формулы 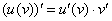 в чистовом оформлении выглядит так:
в чистовом оформлении выглядит так:
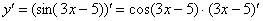
Далее мы берем производную внутренней функции, она очень простая:
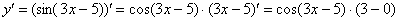
Постоянный множитель обычно выносят в начало выражения:
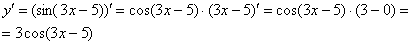
Если осталось какое-либо недопонимание, перепишите решение на бумагу и еще раз прочитайте объяснения.
Пример 7
Найти производную функции 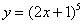
Как всегда записываем:
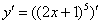
Разбираемся, где у нас внешняя функция, а где внутренняя. Для этого пробуем (мысленно или на черновике) вычислить значение выражения 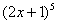 при
при 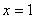 . Что нужно выполнить в первую очередь? В первую очередь нужно сосчитать чему равно основание:
. Что нужно выполнить в первую очередь? В первую очередь нужно сосчитать чему равно основание: 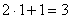 , значит, многочлен
, значит, многочлен 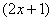 – и есть внутренняя функция:
– и есть внутренняя функция:
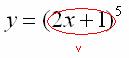
И, только потом выполняется возведение в степень 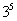 , следовательно, степенная функция – это внешняя функция:
, следовательно, степенная функция – это внешняя функция:
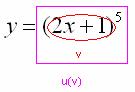
Согласно формуле 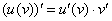 , сначала нужно найти производную от внешней функции, в данном случае, от степени. Разыскиваем в таблице нужную формулу:
, сначала нужно найти производную от внешней функции, в данном случае, от степени. Разыскиваем в таблице нужную формулу: 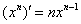 . Повторяем еще раз: любая табличная формула справедлива не только для «икс», но и для сложного выражения. Таким образом, результат применения правила дифференцирования сложной функции
. Повторяем еще раз: любая табличная формула справедлива не только для «икс», но и для сложного выражения. Таким образом, результат применения правила дифференцирования сложной функции 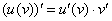 следующий:
следующий:
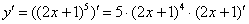
Снова подчеркиваю, что когда мы берем производную от внешней функции 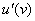 , внутренняя функция
, внутренняя функция 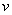 у нас не меняется:
у нас не меняется:
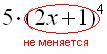
Теперь осталось найти совсем простую производную от внутренней функции и немного «причесать» результат:
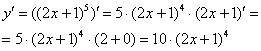
Готово.
Пример 8
Найти производную функции 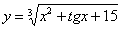
Здесь у нас корень, а для того, чтобы продифференцировать корень, его нужно представить в виде степени 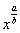 . Таким образом, сначала приводим функцию в надлежащий для дифференцирования вид:
. Таким образом, сначала приводим функцию в надлежащий для дифференцирования вид:
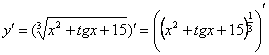
Анализируя функцию, приходим к выводу, что сумма трех слагаемых – это внутренняя функция, а возведение в степень – внешняя функция. Применяем правило дифференцирования сложной функции 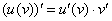 :
:

Степень снова представляем в виде радикала (корня), а для производной внутренней функции применяем простое правило дифференцирования суммы:

Готово.
8.3 ПРОИЗВОДНАЯ ФУНКЦИИ В ТОЧКЕ
Как найти производную функции в точке? Из формулировки следуют два очевидных пункта этого задания:
1) Необходимо найти производную.
2) Необходимо вычислить значение производной в заданной точке.
Пример 9
Вычислить производную функции 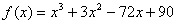 в точке
в точке 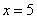
Справка: Следующие способы обозначения функции эквивалентны:
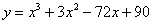
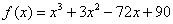
В некоторых задания бывает удобно обозначить функцию «игреком», а в некоторых через «эф от икс».
Сначала находим производную:
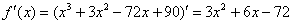
Надеюсь, многие уже приноровились находить такие производные устно.
На втором шаге вычислим значение производной в точке 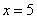 :
:
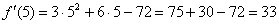
Готово.
ПРАКТИКУМ 8
ЗАДАНИЕ N 1
Тема: Правила дифференцирования
Производная функции 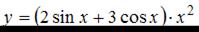 равна …
равна …
Решение:
Для нахождения производной необходимо воспользоваться правилами
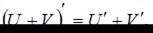
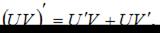
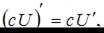 где c – постоянная величина, а U и V – некоторые функции, зависящие от x, и формулами
где c – постоянная величина, а U и V – некоторые функции, зависящие от x, и формулами
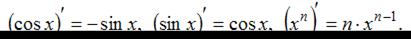
Тогда получим

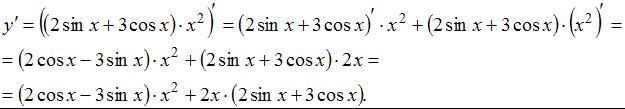
ЗАДАНИЕ N 2
Тема: Правила дифференцирования
Производная функции 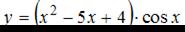 равна …
равна …
Решение:
Для нахождения производной необходимо воспользоваться правилами
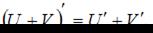
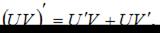
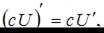 где c – постоянная величина, а U и V – некоторые функции, зависящие от x, и формулами
где c – постоянная величина, а U и V – некоторые функции, зависящие от x, и формулами
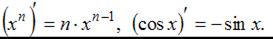
Тогда получим

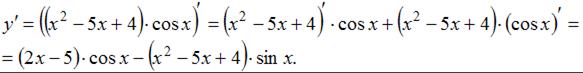
ЗАДАНИЕ N 3
Тема: Правила дифференцирования
Производная функции 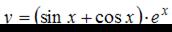 равна …
равна …
Решение:
Для нахождения производной необходимо воспользоваться правилами
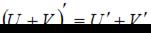 ,
, 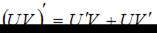 ,
, 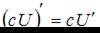 , где c – постоянная величина, а U и V – некоторые функции, зависящие от x, и формулами
, где c – постоянная величина, а U и V – некоторые функции, зависящие от x, и формулами
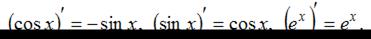
Тогда получим

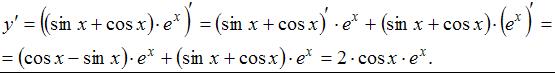
ЗАДАНИЕ N 4
Тема: Правила дифференцирования
Производная функции  равна …
равна …
Решение:
Для нахождения производной необходимо воспользоваться правилами
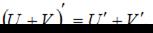
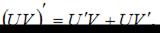
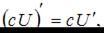 где c – постоянная величина, а U и V – некоторые функции, зависящие от x, и формулами
где c – постоянная величина, а U и V – некоторые функции, зависящие от x, и формулами
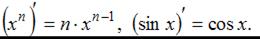
Тогда получим

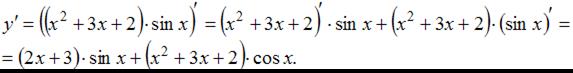
ЗАДАНИЕ N 5
Тема: Производная функции в точке
Если  , то
, то 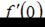 принимает значение, равное …
принимает значение, равное …
Решение:
Производная суммы двух функций равна сумме производных этих функций, значит, 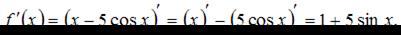 Пусть
Пусть 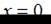 тогда
тогда 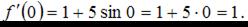
ЗАДАНИЕ N 6
Тема: Производная функции в точке
Если  , то
, то 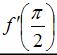 принимает значение, равное …
принимает значение, равное …
Решение:
Производная суммы двух функций равна сумме производных этих функций, значит, 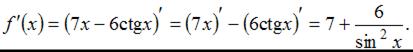 Пусть
Пусть 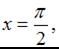 тогда
тогда 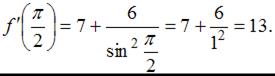
ЗАДАНИЕ N 8
Тема: Производная функции в точке
Если 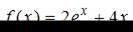 , то
, то 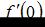 принимает значение, равное …
принимает значение, равное …
Решение:
Напоминаем, что производная суммы двух функций равна сумме производных этих функций. Тогда имеем 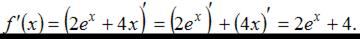
Пусть  . Получим
. Получим 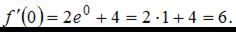
ЗАДАНИЕ N 9
Тема: Производная функции в точке
Если  , то
, то 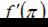 принимает значение, равное …
принимает значение, равное …
Решение:
Производная суммы двух функций равна сумме производных этих функций, значит, 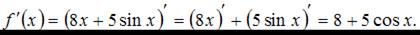 Пусть
Пусть  тогда
тогда 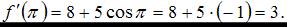
ЗАДАНИЕ N 10
Тема: Производная функции в точке
Если 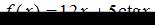 , то
, то 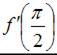 принимает значение, равное …
принимает значение, равное …
Решение:
Производная суммы двух функций равна сумме производных этих функций, значит, 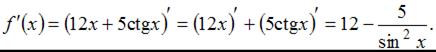 Пусть
Пусть 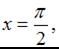 тогда
тогда 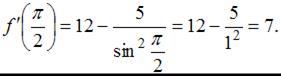
ЗАДАНИЕ N 11
Тема: Производная функции в точке
Если  , то
, то 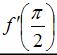 принимает значение, равное …
принимает значение, равное …
Решение:
Производная суммы двух функций равна сумме производных этих функций, значит, 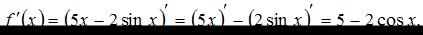 Пусть
Пусть 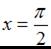 , тогда
, тогда 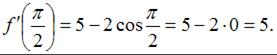
ЗАДАНИЕ N 12
Тема: Производная сложной функции
Производная функции 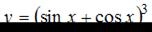 равна …
равна …
Решение:
Данная функция является сложной.
Пусть 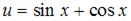 , тогда
, тогда 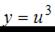 . Напоминаем, что производная сложной функции находится по формуле
. Напоминаем, что производная сложной функции находится по формуле 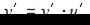 . Тогда получим
. Тогда получим
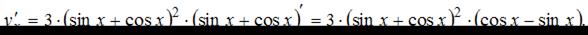
ЗАДАНИЕ N 13
Тема: Производная сложной функции
Производная функции 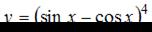 равна …
равна …
Решение:
Данная функция является сложной. Пусть 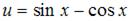 , тогда
, тогда 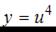 . Напоминаем, что производная сложной функции находится по формуле
. Напоминаем, что производная сложной функции находится по формуле 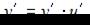 . Тогда получим
. Тогда получим
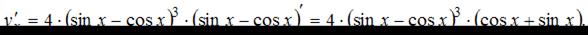
ЗАДАНИЕ N 14
Тема: Производная сложной функции
Производная функции 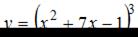 равна …
равна …
Решение:
Данная функция является сложной.
Пусть 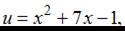 тогда
тогда 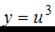 . Напоминаем, что производная сложной функции находится по формуле
. Напоминаем, что производная сложной функции находится по формуле 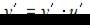 . Тогда получим
. Тогда получим
САМОСТОЯТЕЛЬНАЯ РАБОТА 8
ЗАДАНИЕ N 1
Тема: Правила дифференцирования
Производная функции 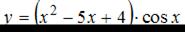 равна …
равна …
ЗАДАНИЕ N 2
Тема: Правила дифференцирования
Производная функции 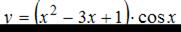 равна …
равна …
ЗАДАНИЕ N 3
Тема: Правила дифференцирования
Производная функции 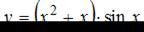 равна …
равна …
ЗАДАНИЕ N 4
Тема: Производная сложной функции
Производная функции 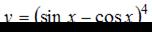 равна …
равна …
ЗАДАНИЕ N 5
Тема: Производная сложной функции
Производная функции 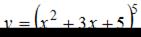 равна …
равна …
ЗАДАНИЕ N 6
Тема: Производная сложной функции
Производная функции 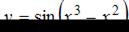 равна …
равна …
ЗАДАНИЕ N 7
Тема: Производная сложной функции
Производная функции 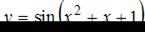 равна …
равна …
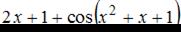
ЗАДАНИЕ N 8
Тема: Производная сложной функции
Производная функции 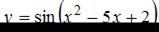 равна …
равна …
ЗАДАНИЕ N 9
Тема: Производная сложной функции
Производная функции 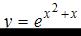 равна …
равна …
ЗАДАНИЕ N 10
Тема: Производная функции в точке
Если  то
то 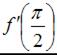 принимает значение, равное …
принимает значение, равное …
ЗАДАНИЕ N 11
Тема: Производная функции в точке
Если 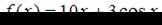 , то
, то 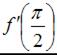 принимает значение, равное …
принимает значение, равное …
ЗАДАНИЕ N 12
Тема: Производная функции в точке
Если 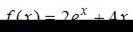 , то
, то 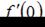 принимает значение, равное …
принимает значение, равное …
ЗАДАНИЕ N 13
Тема: Производная функции в точке
Если  , то
, то 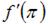 принимает значение, равное …
принимает значение, равное …
ЗАДАНИЕ N 14
Тема: Производная функции в точке
Если  то
то 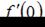 принимает значение, равное …
принимает значение, равное …
Дата: 2019-07-31, просмотров: 433.