В самой примитивной формулировке дифференциал – это «почти то же самое, что и производная».
Производная функции чаще всего обозначается через 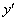 .
.
Дифференциал функции стандартно обозначается через 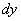 (так и читается – «дэ игрек»)
(так и читается – «дэ игрек»)
Дифференциал функции одной переменной записывается в следующем виде:
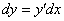
Другой вариант записи: 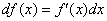
Простейшая задача: Найти дифференциал функции 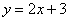
1) Первый этап. Найдем производную:
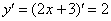
2) Второй этап. Запишем дифференциал:
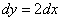
Готово.
Дифференциал функции одной или нескольких переменных чаще всего используют для приближенных вычислений.
Для приближенного вычисления значения функции y(x) в точке 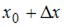 можно использовать формулу:
можно использовать формулу: 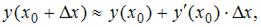 где
где 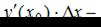 приращение функции в точке
приращение функции в точке  Функция y(x) определяется из условия задачи Значения
Функция y(x) определяется из условия задачи Значения  и
и 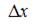 выбираются так, чтобы можно было вычислить
выбираются так, чтобы можно было вычислить 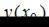 и при этом
и при этом  , взятое по модулю, было бы как можно меньше.
, взятое по модулю, было бы как можно меньше.
10.2 ПРИБЛИЖЕННОЕ ДИФФЕРЕНЦИРОВАНИЕ
Для того, чтобы получить простейшую приближенную формулу для производной, нужно знать только ее определение:
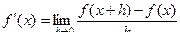 . (3.1)
. (3.1)
При малом h можно положить:
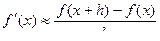 . (3.2)
. (3.2)
Это и есть простейшая приближенная формула.
В определении (3.1) h может принимать значения обоих знаков. В дискретной записи принято обозначать через h положительное число, так что можно написать еще одну формулу:
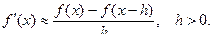 (3.2´)
(3.2´)
Какую ошибку мы совершаем, заменяя производную разностным отношением по формуле (3.2)? Это легко сообразить. Напишем:
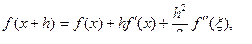
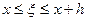 .
.
Отсюда
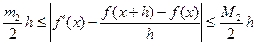 ,
,
где m2=min | 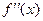 |, M2 = max |
|, M2 = max | 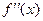 |. При
|. При 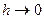 ошибка стремится к нулю со скоростью h или, как говорят, формула (3.2) имеет первый порядок точности. Сложением формул (3.2) и (3.2') получается симметричная формула:
ошибка стремится к нулю со скоростью h или, как говорят, формула (3.2) имеет первый порядок точности. Сложением формул (3.2) и (3.2') получается симметричная формула:
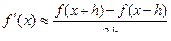 . (3.3)
. (3.3)
Формула (3.3), как легко проверить, точнее формулы (3.2), а именно, ошибка здесь имеет порядок 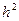 — это есть формула второго порядка точности потому, что ошибка не превосходит
— это есть формула второго порядка точности потому, что ошибка не превосходит 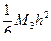 , где M3 = max |
, где M3 = max |  |. Это увеличение точности получилось только за счет симметрии. Это случается очень часто.
|. Это увеличение точности получилось только за счет симметрии. Это случается очень часто.
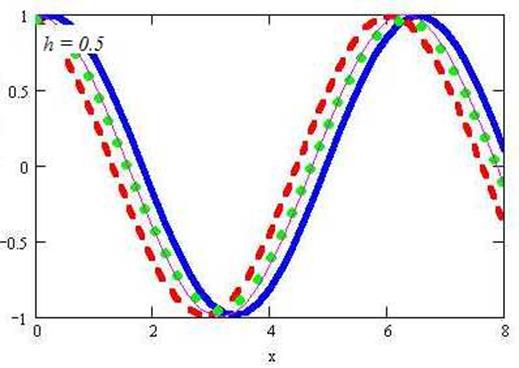
Рис. 1.
На рисунке 1 приведены результаты вычисления производной функции f(x) = sin(x) по трем разностным формулам (3.2, 3.2´ и 3.3) вместе с точным графиком производной.
ПРАКТИКУМ 10
ЗАДАНИЕ N 1
Тема: Дифференциал функции
Для приближенного вычисления значения функции y(x) в точке 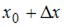 можно использовать формулу
можно использовать формулу 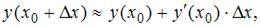 где
где 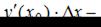 приращение функции в точке
приращение функции в точке 
Функция y(x) определяется из условия задачи.
Значения  и
и 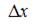 выбираются так, чтобы можно было вычислить
выбираются так, чтобы можно было вычислить  и при этом
и при этом  , взятое по модулю, было бы как можно меньше.
, взятое по модулю, было бы как можно меньше.
Тогда приближенное значение выражения 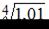 равно …
равно …
Решение:
 .
.  Так как
Так как 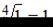 , то можно рассмотреть функцию
, то можно рассмотреть функцию 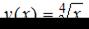
Пусть  тогда
тогда 
Имеем: 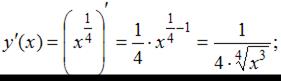
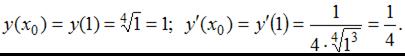
По формуле 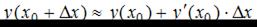
получим 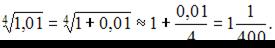
ЗАДАНИЕ N 2
Тема: Дифференциал функции
Для приближенного вычисления значения функции y(x) в точке 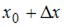 можно использовать формулу:
можно использовать формулу: 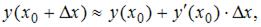 где
где 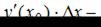 приращение функции в точке
приращение функции в точке  Функция y(x) определяется из условия задачи Значения
Функция y(x) определяется из условия задачи Значения  и
и 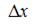 выбираются так, чтобы можно было вычислить
выбираются так, чтобы можно было вычислить 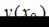 и при этом
и при этом  , взятое по модулю, было бы как можно меньше.
, взятое по модулю, было бы как можно меньше.
Тогда наилучшее приближенное значение выражения 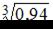 равно …
равно …
Решение:
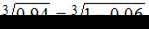 .
.  Так как
Так как 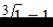 , то можно рассмотреть функцию
, то можно рассмотреть функцию 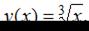
Для  имеем:
имеем: 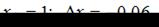 Тогда
Тогда 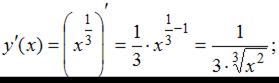
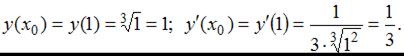 По формуле
По формуле 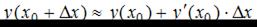 получим
получим 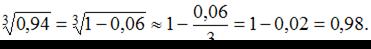
ЗАДАНИЕ N 3
Тема: Дифференциал функции
Для приближенного вычисления значения функции y(x) в точке 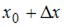 можно использовать формулу:
можно использовать формулу: 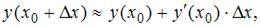 где
где 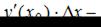 приращение функции в точке
приращение функции в точке  Функция y(x) определяется из условия задачи. Значения
Функция y(x) определяется из условия задачи. Значения  и
и 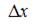 выбираются так, чтобы можно было вычислить
выбираются так, чтобы можно было вычислить 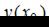 и при этом
и при этом  , взятое по модулю, было бы как можно меньше.
, взятое по модулю, было бы как можно меньше.
Тогда наилучшее приближенное значение выражения 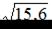 равно …
равно …
Решение:
 . Так как
. Так как  , то можно рассмотреть функцию
, то можно рассмотреть функцию 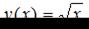
Для 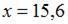 имеем:
имеем:  Тогда
Тогда 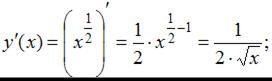
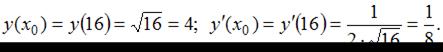
По формуле 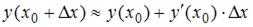 получим:
получим: 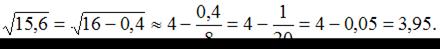
САМОСТОЯТЕЛЬНАЯ РАБОТА 10
ЗАДАНИЕ N 1
Тема: Дифференциал функции
Для приближенного вычисления значения функции y(x) в точке 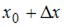 можно использовать формулу:
можно использовать формулу: 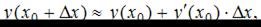 где
где 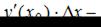 приращение функции в точке
приращение функции в точке  Функция y(x) определяется из условия задачи. Значения
Функция y(x) определяется из условия задачи. Значения  и
и 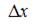 выбираются так, чтобы можно было вычислить
выбираются так, чтобы можно было вычислить 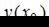 и при этом
и при этом  , взятое по модулю, было бы как можно меньше.
, взятое по модулю, было бы как можно меньше.
Тогда наилучшее приближенное значение выражения  равно …
равно …
ЗАДАНИЕ N 2
Тема: Дифференциал функции
Для приближенного вычисления значения функции y(x) в точке 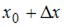
можно использовать формулу: 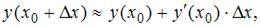 где
где 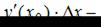 приращение функции в точке
приращение функции в точке  Функция y(x) определяется из условия задачи. Значения
Функция y(x) определяется из условия задачи. Значения  и
и 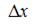 выбираются так, чтобы можно было вычислить
выбираются так, чтобы можно было вычислить 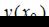 и при этом
и при этом 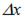 , взятое по модулю, было бы как можно меньше.
, взятое по модулю, было бы как можно меньше.
Тогда наилучшее приближенное значение выражения 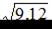 равно …
равно …
ЗАДАНИЕ N 3
Тема: Дифференциал функции
Для приближенного вычисления значения функции y(x) в точке  можно использовать формулу
можно использовать формулу 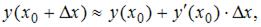 где
где 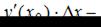 приращение функции в точке
приращение функции в точке 
Функция y(x) определяется из условия задачи.
Значения  и
и 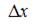 выбираются так, чтобы можно было вычислить
выбираются так, чтобы можно было вычислить 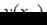 и при этом
и при этом 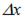 , взятое по модулю, было бы как можно меньше.
, взятое по модулю, было бы как можно меньше.
Тогда приближенное значение выражения  равно …
равно …
ЗАДАНИЕ N 4
Тема: Дифференциал функции
Для приближенного вычисления значения функции y(x) в точке  можно использовать формулу
можно использовать формулу 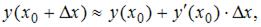 где
где 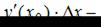 приращение функции в точке
приращение функции в точке 
Функция y(x) определяется из условия задачи.
Значения  и
и 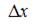 выбираются так, чтобы можно было вычислить
выбираются так, чтобы можно было вычислить 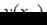 и при этом
и при этом 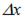 , взятое по модулю, было бы как можно меньше.
, взятое по модулю, было бы как можно меньше.
Тогда приближенное значение выражения 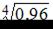 равно …
равно …
РАЗДЕЛ 4
Дата: 2019-07-31, просмотров: 334.