Решить систему по формулам Крамера.
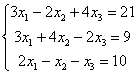
Решение:
Решим систему по формулам Крамера.
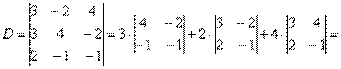
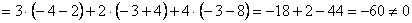 , значит, система имеет единственное решение.
, значит, система имеет единственное решение.

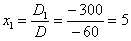



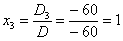
Ответ:  .
.
ЗАДАНИЕ 7
Решить систему линейных уравнений методом Гаусса
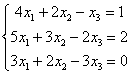
Запишем расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду:
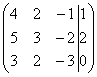
Смотрим на левую верхнюю «ступеньку». Там у нас должна быть единица. Проблема состоит в том, что в первом столбце единиц нет вообще, поэтому перестановкой строк ничего не решить. В таких случаях единицу нужно организовать с помощью элементарного преобразования. Обычно это можно сделать несколькими способами. Я поступил так: (1) К первой строке прибавляем вторую строку, умноженную на –1. То есть, мысленно умножили вторую строку на –1 и выполнили сложение первой и второй строки, при этом вторая строка у нас не изменилась.
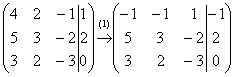
Теперь слева вверху –1, что нас вполне устроит. Кто хочет получить +1, может выполнить дополнительное телодвижение: умножить первую строку на –1 (сменить у неё знак).
Дальше алгоритм работает уже по накатанной колее:
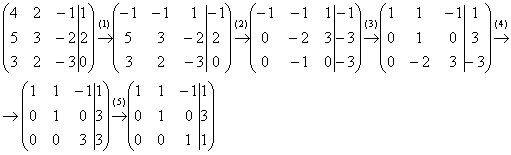
(2) Ко второй строке прибавили первую строку, умноженную на 5. К третьей строке прибавили первую строку, умноженную на 3.
(3) Первую строку умножили на –1, в принципе, это для красоты. У третьей строки также сменили знак и переставили её на второе место, таким образом, на второй «ступеньке у нас появилась нужная единица.
(4) К третьей строке прибавили вторую строку, умноженную на 2.
(5) Третью строку разделили на 3.
Скверным признаком, который свидетельствует об ошибке в вычислениях (реже – об опечатке), является «плохая» нижняя строка. То есть, если бы у нас внизу получилось что-нибудь вроде 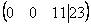 , и, соответственно,
, и, соответственно, 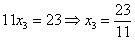 , то с большой долей вероятности можно утверждать, что допущена ошибка в ходе элементарных преобразований.
, то с большой долей вероятности можно утверждать, что допущена ошибка в ходе элементарных преобразований.
Заряжаем обратный ход, в оформлении примеров часто не переписывают саму систему, а уравнения «берут прямо из приведенной матрицы». Обратный ход, напоминаю, работает, снизу вверх:
Да тут подарок получился:
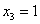
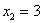

Ответ: 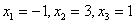 .
.
САМОСТОЯТЕЛЬНАЯ РАБОТА 3
ЗАДАНИЕ N 1
Тема: Правило Крамера
Систему 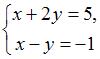 решают по правилу Крамера.
решают по правилу Крамера.
Вычислите: 1) 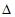 2)
2) 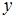 3)
3) 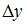 4) x
4) x
ЗАДАНИЕ N 2
Тема: Правило Крамера
Систему 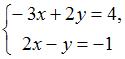 решают по правилу Крамера.
решают по правилу Крамера.
Вычислите: 1) 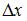 2)
2) 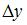 3) x 4) y
3) x 4) y
ЗАДАНИЕ N 3
Правило Крамера
Систему 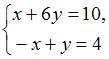 решают по правилу Крамера.
решают по правилу Крамера.
Установите соответствие между названиями величин и их значениями.
1) 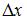
2) 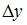
3) x
4) y
| 1 | 2 | 3 | 4 | 5 |
| - 14 | 14 | - 2 | 2 | 1 |
ЗАДАНИЕ N 4
Правило Крамера
Систему 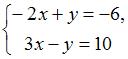 решают по правилу Крамера.
решают по правилу Крамера.
Установите соответствие между названиями величин и их значениями.
1) 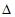
2) 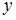
3) 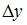
4) x
| 1 | 2 | 3 | 4 | 5 |
| - 1 | 2 | - 2 | 4 | 1 |
ЗАДАНИЕ N 5
Тема: Системы линейных уравнений
Система линейных уравнений
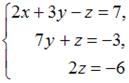 имеет решение …
имеет решение …
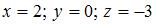
ЗАДАНИЕ N 6
Тема: Системы линейных уравнений
Система линейных уравнений  имеет решение …
имеет решение …

ЗАДАНИЕ N 7
Тема: Системы линейных уравнений
Система линейных уравнений  имеет решение …
имеет решение …
ЗАДАНИЕ N 8
Тема: Системы линейных уравнений
Система линейных уравнений 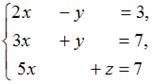 имеет решение …
имеет решение …
ЗАДАНИЕ N 9
Тема: Системы линейных уравнений
Система линейных уравнений  имеет решение …
имеет решение …
ЗАДАНИЕ N 10
Решить систему линейных уравнений методом Гаусса
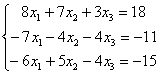
Дата: 2019-07-31, просмотров: 348.