Для более сложных физических явлений, таких как процессы колебания, волновые процессы, процессы теплопроводности не всегда удается построить такие простенькие модельки. Реально эти процессы описываются дифференциальными уравнениями 2 порядка, уравнениями в частных производных, называемых уравнениями матфизики.
Напомню, что дифференциальным уравнением называется уравнение, куда входит искомая функция со своими производными
F(x,y(x),y'(x),y''(x):y(n)(x))=0
Наивысший порядок производной, входящей в уравнение, называется порядком дифференциального уравнения. Решением дифура является не число, а функция, x называется независимой переменной. Если искомая функция является функцией одной переменной, то дифуравнение называется обыкновенным дифуравнением, если искомая функция является функцией нескольких переменных, то дифуравнение называется уравнением в частных производных.
В случае двух независимых переменных x и y уравнения матфизики, которые являются как правило уравнениями первого и второго порядков, линейными относительно входящих в них производных можно записать в виде
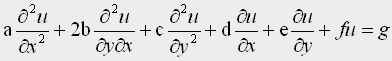
В случае двух независимых переменных x и y уравнения матфизики, которые являются как правило уравнениями первого и второго порядков, линейными относительно входящих в них производных можно записать в виде
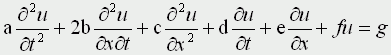
Обычно одна из переменных - это время t.
5. Классификация уравнений матфизики
Различают типы уравнений в зависимости от соотношения между коэффициентами.
1) При a=b=c=f=0, d не 0, e не 0 получаем уравнение первого порядка вида
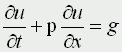
называемое уравнением переноса. Такие уравнения описывают процессы переноса частиц в различных средах, распространение возмущений и т.д. Искомая функция u=u(t,x) зависит от времени и от пространственной переменной, коэффициент p характеризует скорость переноса.
2) Если хотя бы один из коэффициентов a,b,c будет отличен от нуля, то уравнение будет иметь второй порядок и в зависимости от знака дискриминанта
D=b2-4ac
Будет принадлежать к одному из трех типов
D>0 - гиперболическое,
D=0 - параболическое,
D<0 - эллиптическое.
А) Гиперболическое уравнение
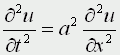
Называется волновым, оно описывает различные виды колебаний. Если в уравнение входит одна пространственная переменная, то оно описывает продольные колебания стержня, а также поперечные колебания струны. В этом случае a2=T/ρ, где T - это натяжение струны, а ρ - ее линейная плотность. Двухмерное волновое уравнение используется для описания колебаний тонкой пластины (мембраны)
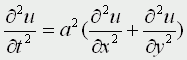
Трехмерное волновое уравнение
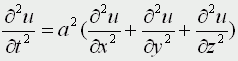
Описывает распространение волн в пространстве (например звуковые волны в различных средах, упругие волны в сплошной среде и т.д.)
Б) параболическое уравнение
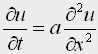
называется уравнением теплопроводности или диффузии с помощью него описываются различные процессы, связанные с передачей чего-либо: передачей тепла, передачей импульса, передачей энергии.
В) Эллиптическое уравнение
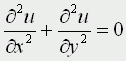
Уравнение Лапласа
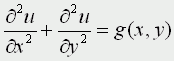
Уравнение Пуассона
К уравнениям такого типа приводят стационарные, не зависящие от времени, физические задачи (исследования потенциальных течений жидкости, определение формы нагруженной мембраны и т.д.)
Решение подобных уравнений удобно проводить методом сеток. Рассмотрим это на примере моделирования температурного поля.
Обозначим температуру стержня в точке с координатой х в момент времени t через u(x,t). Уравнение теплопроводности имеет вид
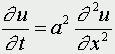
где а - коэффициент температуропроводности, зависящий в первую очередь от вещества, из которого сделан стержень.
Уравнение теплопроводности сопровождается начальными и граничными (краевыми) условиями, делающими постановку задачи физически однозначной Известно, что если для дифференциального уравнения заданы начальные условия (условия в начальный момент времени), то такая задача называется задачей Коши, если же заданы граничные (краевые) условия (на границах исследуемой области), то такая задача называется краевой задачей, если заданы и начальные и граничные условия, то мы имеем смешанную краевую задачу.
Начальное условие задает распределение температуры в стержне в начальный момент времени (считаем его равным нулю):
u(x,0) = φ(x)
Краевые условия (их должно быть в данном случае два) указывают, в простейшем варианте, какая температура поддерживается на концах стержня:
u(0,t)= ψ 0(t), u(l,t)= ψ l (t)
Заметим, что начальные и граничные условия должны быть согласованы, т.е.
u(0,0) = φ(0)=ψ0(0)
u(l,0) = φ(l)=ψl(0)
Моделирование процесса теплопроводности связано с дискретизацией как временного изменения температуры, так и пространственного.
Введем равномерную прямоугольную сетку с помощью координатных линий
xi=ih, i=0,1,....n,
tj=j τ , j=0,1,....m,
где h - это шаг по пространству, по координате х, а τ - шаг по времени.
Значения функции в узлах сетки обозначим uij=u(xi,tj).
Входящие в уравнение производные заменим их конечно-разностными приближениями (аппроксимациями)
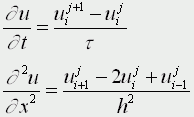
получим
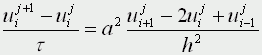
или

где
i=1,2,:.n-1,
j=0,1,:.m-1.
Получилась явная разностная схема, удобная в применении, но устойчивая лишь при выполнении условия
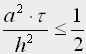
Это следует учитывать, выбирая шаги по времени и пространству.
Совокупность узлов в фиксированный момент времени называется слоем.
Построенная схема позволяет нам находить значение функции температур на j+1 слое через значения на j слое. Для начало счета при j=0 необходимо знать значения функции температур на нулевом слое. Они нам известны из начальных условий.
Если использовать другие конечно разностные соотношения для аппроксимации производных,
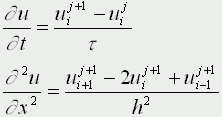
то получим существенно более устойчивую неявную схему
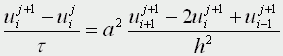
или
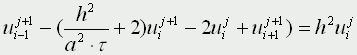
В отличие от явной схемы каждое разностное уравнение второй схемы содержит на каждом новом слое три неизвестные значения, которые невозможно определить сразу же, как мы поступали в явной схеме. При этом вторая разностная схема состоит из линейных трех точечных уравнений, т.е. каждое уравнение содержит неизвестную функцию в трех точках нового слоя. Такие системы линейных уравнений, системы с трехдиагональной матрицей, могут быть легко решены методом прогонки. Таким образом, в случае неявной схемы, чтобы посчитать значения функции температур в каждый следующий момент времени, т.е., чтобы перейти на следующий слой по времени, необходимо каждый раз решать методом прогонки линейную систему.
Это - система линейных алгебраических уравнений с трехдиагональной матрицей. Для ее решения наиболее эффективен метод прогонки.
Так можно моделировать физические явления применяя математический аппарат во всей его мощи. Однако это довольно сложно. При моделировании явления теплопроводности можно пойти другим путем.
Пусть задана квадратная пластина, на краях которой известна температура. Требуется определить температуру во внутренних точках. Если предположить, что теплоотвода внутри нет, то можно смоделировать решение путем вычисления среднего значения T=(t1+t2+t3+t4)/4.
Однако это очень грубое приближение, ведь в разных точках пластины температура различна.
Разобьем квадрат на четыре части и для каждого малого квадратика применим ту же процедуру:
T11 = (t1 + T12 + T21 + t4)/4
T12 = (t1 + T11 + T22 + t2)/4
T21 = (t4 + T11 + T22 + t3)/4
T22 = (t2 + T21 + T12 + t3)/4
Или в другом виде
4T11 - T12 - T21 = t1 + t4
-T11 + 4T12 - T22 = t1 + t2
-T11 + 4T21 - T22 = t3 + t4
-T12 - T21 + 4T22 = t2 + t3
который представляет систему линейных уравнений относительно неизвестных T11, Т.
Для решения задачи по определению температур в точках твердого тела нами использован математический пакет MathCAD, имеющий встроенную функцию relax, которая реализует метод, описанный выше и называемый методом сеток.
Определим поле в плоской неоднородно нагретой пластине методм сеток в программе MathCAD.
Введем равномерную прямоугольную сетку с помощью координатных линий в рассматриваемую область пространства (Рис.1). Шаги по координатным осям OX и OY
xi = x 0+ ih , i =0,±1,..., ± n ,
yi = y 0+ kl , k =0,±1,..., ± m ,
Значения функции в узлах сетки обозначим как ui k =u(xi,t k ).
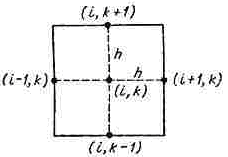
Рисунок 1 – Построение сетки
Зададим граничные условия, число точек и шаг дискретизации

и построим матрицу температур на границе, внутри которой нулевые значения это искомые температуры
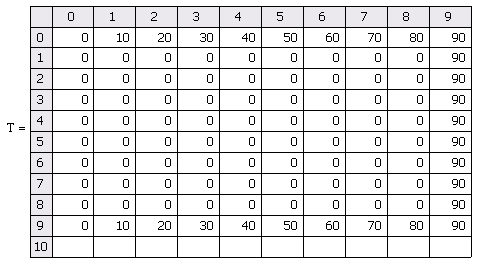
Рисунок 2 – Задание граничных условий задачи
Проведем решение встроенным оператором вводя в него обозначенную функцию с целью найти температурное поле внутри тела и рекомендуемые параметры a, b, c, d, f.

Решение дает следующие результаты, представленные таблицей
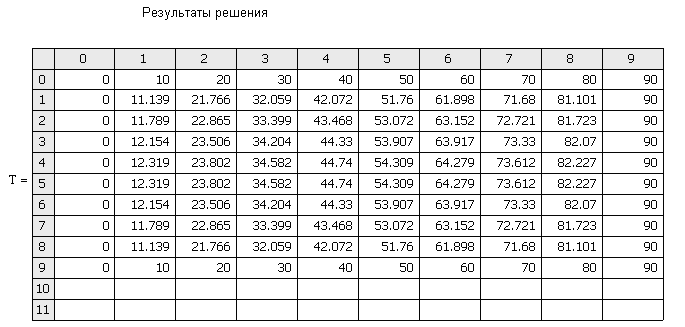
Рисунок 2 – Табличное представление распределения температуры в твердом теле, найденное методом сеток
Эти результаты можно представить графически трехмерным массивом
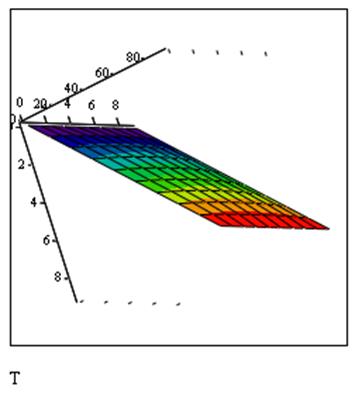
Рисунок – Температурное поле в твердом теле
Дата: 2019-07-30, просмотров: 389.