План лекции:
Понятие случайных событий
Вычисление площадей методом Монте-Карло
Задача Бюффона
Модели случайных и хаотических блужданий
1. Понятие случайных событий
В вероятностных моделях смена состояний моделируемой системы определяется случайными величинами.
Событие называется случайным, если оно достоверно непредсказуемо. Случайность окружает наш мир и чаще всего играет отрицательную роль в нашей жизни. Однако есть обстоятельства, в которых случайность может оказаться полезной.
Одним из распространенных приближенных методов решения задач вычислительной математики является случайный метод, называемый метод Монте-Карло. Сущность метода заключается в том, что для решения какой-либо математической задачи, связанной с вычислением числа I, строится некоторая случайная величина ξ, такая, что математическое ожидание этой случайной величины E(ξ) является значением искомого решения. Проведя серию вычислительных экспериментов со случайной величиной ξ, мы можем найти приближенное решение как среднее значение результатов эксперимента.
2. Вычисление площадей методом Монте-Карло
С помощью этого метода можно найти площадь любой фигуры G, которая имеет сложный контур, который сложно описать аналитически или сложно проинтегрировать. Нужно вписать эту фигуру в фигуру известной площади, скажем в прямоугольник со сторонами a b и бросать точку на эту фигуру. Вероятность попадания точки в G будет равна отношению площадей.
3. Задача Бюффона
Также с помощью случайного метода можно вычислить число π.
Для этого необходимо решить задачу Бюффона. Французский математик Бюффон (XYIII в.) определил, что если на поле, разграфленное параллельными прямыми, расстояние между которыми L, бросается наугад игла длиной l, то вероятность того, что игла пересечет хотя бы одну прямую, определяется формулой: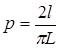 
Эта задача дала способ вычисления числа π.
Действительно, если L=2l, то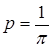 
.
Таким образом, автором было вычислено 200 знаков после запятой числа π. Точность получаемого решения зависит от количества проведенных экспериментов.
Задачу Бюффона можно легко смоделировать на компьютере
Известно, что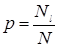 
, где 
- число бросаний,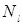 
- число пересечений иглы с линиями.
Как определить, пересекла игла прямую или нет? Положение иглы можно однозначно определить заданием координаты центра иглы y=0 из [-l/2,l/2] и угла α, задаваемых случайным образом. Тогда координаты концов иглы определяются по следующим формулам:
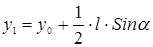
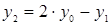
Условие пересечения прямой - y1∙y2<0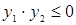 
4. Модели случайных и хаотических блужданий
На случайности основана так называемая "модель пьяницы", которая используется для моделирования всевозможных хаотических движений частиц скажем движений молекул каких-либо газов или жидкостей, с помощью этой модели моделируются многие химические и физические процессы, проходящие в дискретных средах - в газах и жидкостях - явления диффузии, всевозможные потоки частиц, ветер, водопад, взрыв и т.д.
Есть точка на прямой, имеющая начальную координату x0, которая движется вправо или влево в зависимости от случайной величины r из интервала [0,1] если r>0,5, то точка делает шаг вправо x1=х0+h, в противном случае x1=x0-h. Шаг может быть как постоянный, так и переменный. Значение шага в свою очередь может быть случайное число из интервала [0,hmax].
Точка может двигаться по плоскости, может быть n точек - получается модель броуновского движения. Можно ввести различные скорости движения частиц, можно изменять условие, скажем если ri>0,8, то точка делает шаг вправо x1=х0+h, в противном случае x1=x0-h. - получим модель поступательного движения частиц вправо - стая комаров, подхваченных ветром. Если первоначально все частицы сконцентрировать в одной точке, а потом пронаблюдать их распространение - то это будет модель взрыва. Если провести вертикальную черту - перегородку, и частицы по разную строну перегородки закрасить разным цветом - получим модель диффузии - смешивания различных газов или жидкостей и т.д.
В модели пьяницы не предусматривается столкновение частиц.
Если случайным образом задать первоначальное положение частиц, направление их движения и скорость и определить, что далее частица будет двигаться равномерно и прямолинейно до столкновения с другой частицей, а в случае столкновения произойдет зеркальное упругое отражение, то получим модель движения частиц, называемую моделью бильярдного шара. Эта модель описывает поведение идеального газа. С помощью этой модельки можно посчитать, допустим, давление газа на стенки сосуда - ограничить частицы прямоугольником (количество частиц установить пропорциональным плотности газа), предусмотреть зеркальное отражение частиц от стенок и посчитать число ударов в стенки сосуда. Давление газа будет пропорционально числу ударов о стенки.
Компьютерное моделирование при решении задач массового обслуживания, реализуемое в виде метода статистических испытаний (метода Монте-Карло), хоть и не является в теории массового обслуживания основным, но играет в ней важную роль. Основная линия в ней - получение результатов аналитических, т.е. представленных формулами. Однако, возможности аналитических методов весьма ограничены, в то время как метод статистических испытаний универсален и весьма прост для понимания (по крайней мере кажется таковым).
2. Очередь к одному "продавцу"
Рассмотрим одну из простейших задач данного класса. Имеется магазин с одним продавцом, в который случайным образом входят покупатели. Если продавец свободен, он начинает обслуживать покупателя сразу, если покупателей несколько, выстраивается очередь.
Вот аналогичные задачи:
ремонтная зона в автохозяйстве и автобусы, сошедшие с линии из-за поломки;
травмопункт и больные, пришедшие на прием по случаю травмы (т.е. без системы предварительной записи);
телефонная станция с одним входом (или одной телефонисткой) и абоненты, которых при занятом входе ставят в очередь (такая система иногда практикуется);
сервер локальной сети и персональные машины на рабочем месте, которые шлют сообщение серверу, способному воспринять разом и обработать не более одного сообщения.
Будем для определенности говорить о магазине, покупателях и продавце. Рассмотрим возникающие здесь проблемы, которые заслуживают математического исследования и, как выясняется, весьма серьезного.
Итак, на входе этой задачи случайный процесс прихода покупателей в магазин. Он является "марковским", т.е. промежутки между приходами любой последовательной пары покупателей - независимые случайные события, распределенные по некоторому закону. Реальный характер этого закона может быть установлен лишь путем многочисленных наблюдений; в качестве простейшей модельной функции плотности вероятности можно взять равновероятное распределение в диапазоне времени от 0 до некоторого T - максимально возможного промежутка между приходами двух последовательных покупателей. При этом распределении вероятность того, что между приходами двух покупателей пройдет 1 минута, 3 минуты или 8 минут одинакова (если T > 8).
Такое распределение, конечно, малореалистично; реально оно имеет при некотором значении t = τ максимум и быстро спадает при больших t, т.е. имеет вид, изображенный на рис. 1.
Можно, конечно, подобрать немало элементарных функций, графики которых похожи на тот, что изображен на рис. 1. Например, семейство функций Пуассона, широко используемых в теории массового обслуживания:
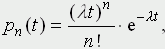(1)
где λ - некоторая константа, n - произвольное целое.Функции (1) имеют максимум при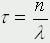 
и нормированы: 
.
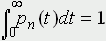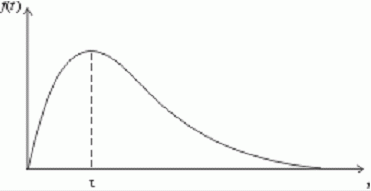
Рис. 1. Типичная плотность вероятности распределения времени между приходами покупателей
Второй случайный процесс в этой задаче, никак не связанный с первым, сводится к последовательности случайных событий - длительностей обслуживания каждого из покупателей. Распределение вероятностей длительности обслуживания качественно имеет тот же вид, что и в предыдущем случае; при отработке первичных навыков моделирования методом статистических испытаний вполне уместно принять модель равновероятного распределения.
В таблице 1 в колонке A записаны случайные числа - промежутки между приходами покупателей (в минутах), в колонке B - случайные числа - длительности обслуживания (в минутах). Для определенности взято amax = 10 и bmax = 5. Из этой короткой таблицы, разумеется, невозможно установить, каковы законы распределения приняты для величин A и B; в данном обсуждении это не играет никакой роли. Остальные колонки предусмотрены для удобства анализа; входящие в них числа находятся путем элементарного расчета. В колонке C представлено условное время прихода покупателя, в колонке D - момент начала обслуживания, E - момент конца обслуживания, F - длительность времени, проведенного покупателем в магазине в целом, G - в очереди в ожидании обслуживания, H - время, проведенное продавцом в ожидании покупателя (магазин пуст). Таблицу удобно заполнять по горизонтали, переходя от строчки к строчке. Приведем для удобства соответствующие формулы (в них i = 1, 2, 3, ...):
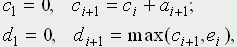
- так как начало обслуживания очередного покупателя определяется либо временем его прихода, если магазин пуст, либо временем ухода предыдущего покупателя;
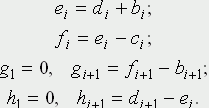
N A B C D E F G H
1 0 4 0 0 4 4 0 0
2 2 1 2 4 5 3 2 0
3 10 5 12 12 17 5 0 7
4 1 2 13 17 19 6 4 0
5 6 3 19 19 22 3 0 0
Табл 1. Моделирование очереди.
Таким образом, при данных случайных наборах чисел в колонках A и B и покупателям приходилось стоять в очереди (колонка G), и продавцу - в ожидании покупателя (колонка H).
При моделировании систем такого вида возникают следующие вопросы. Какое среднее время приходится стоять в очереди к прилавку? Чтобы ответить на него, следует найти
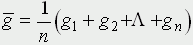
в некоторой серии испытаний. Аналогично можно найти среднее значение величины h. Конечно, эти выборочные средние сами по себе - случайные величины; в другой выборке того же объема они будут иметь другие значения (при больших объемах выборки, не слишком отличающиеся друг от друга). Доверительные интервалы, в которых находятся точные средние значения (т.е. математические ожидания соответствующих случайных величин) при заданных доверительных вероятностях находятся методами математической статистики.
Сложнее ответить на вопрос, каково распределение случайных величин G и H при заданных распределениях случайных величин A и B. Допустим, в простейшем моделировании мы примем гипотезу о равновероятных распределениях величин A и B - скажем, для A в диапазоне от 0 до 10 минут и B - от 0 до 5 минут. Для построения методом статистических испытаний распределений величин G и H поступим так: найдем в достаточно длинной серии испытаний (реально - в десятках тысяч, что на компьютере делается достаточно быстро) значения gmax (для H все делается аналогично) и разделим промежуток [0, gmax] на m равных частей - скажем, вначале на 10 - так, чтобы в каждую часть попало много значений gi. Разделив число попаданий nk в каждую из частей на общее число испытаний n, получим набор чисел
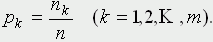
Построенные по ним гистограммы дают представление о функциях плотностей вероятности соответствующих распределений. По гистограмме можно составить представление о функции плотности распределения соответствующей случайной величины. Для проверки же гипотезы о принадлежности такого эмпирически найденного распределения тому или иному конкретному виду служат известные статистические критерии.
Располагая функцией распределения (пусть даже эмпирической, но достаточно надежной), можно ответить на любой вопрос о характере процесса ожидания в очереди. Например: какова вероятность прождать дольше m минут? Ответ будет получен, если найти отношение площади криволинейной трапеции, ограниченной графиком плотности распределения, прямой x = m и y = 0, к площади всей фигуры.
Программа моделирование очереди позволяет моделировать описанный выше процесс. На выходе она дает средние значения и дисперсии случайных величин g и h, полученные по выборке, максимальный объем которой порядка 10000 (ограничение связано с малой допустимой длиной массива в PASCALе; чтобы его смягчить, использовано динамическое описание массивов g и h). Кроме того, программа строит гистограммы распределений величин g и h.
ТЕМА 2
Дата: 2019-07-30, просмотров: 237.
