Движение электрических зарядов в проводящей среде характеризуется плотностью электрического тока j. С постоянным (стационарным) током неразрывно связано электрическое и магнитное поле. Эти поля формально не зависят друг с другом и могут рассматриваться отдельно. Здесь ограничимся анализом электрического поля, которое является потенциальным.
Задачи растекания токов решаются в инженерной практике при исследовании полей различных проводящих систем, при расчете сопротивления заземления (утечки), в линиях передачи и др. Величины, представляющие интерес при анализе, включают напряжение, плотность тока, проводимость утечки, мощность тепловыделения (джоулевы потери).
Постановка задачи растекания токов: Задача формулируется в виде уравнения Пуассона относительно скалярного электрического потенциала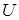 
(предполагается, что вектор плотности тока лежит в плоскости модели). Для плоскопараллельных задач уравнение имеет вид:
,
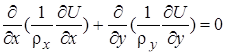а для осесимметричного случая:
,
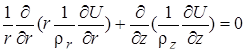где компоненты тензора удельного электрического сопротивления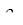 
, 
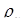или 
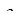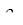, - постоянные величины в пределах блоков модели. В теоретических исследованиях вместо 
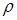принято рассматривать обратную величину – удельную проводимость вещества 
.
Вектор плотности тока 
определяется уравнением:
.
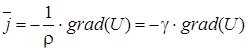Свойства сред: диэлектрик (воздух), изотропные и ортотропные материалы с постоянной электропроводностью.
Источники поля в задачах растекания токов: электроды с заданным потенциалом, сторонние токоподводы. Под источниками поля понимают сторонние токи, заданные на границах проводника. В рамках комплекса ELCUT источники поля могут быть заданы вдоль рёбер и в отдельных вершинах модели.
Плотность тока, заданная в точке плоскости xy соответствует токоподводу в виде тонкого проводника, перпендикулярного плоскости модели. Он описывается своей линейной плотностью тока.
В осесимметричном случае источник, заданный в вершине, описывает токоподвод в виде тонкого кольца с осью, совпадающей с осью симметрии задачи или точечный токовый ввод, если точка лежит на оси вращения. В этих двух случаях источник характеризуется величиной подводимого тока I. Для кольцевого токоподвода радиуса r полное значение тока связано с его линейной плотностью соотношением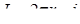 
. Задание поверхностной плотности тока на рёбрах в плоскости модели эквивалентно неоднородному граничному условию Неймана и осуществляется с его помощью.
Граничные условия в задачах растекания токов: В задачах растекания токов на внешних и внутренних рёбрах модели могут быть заданы следующие виды граничных условий.
Условие Дирихле задает известное значение электрического потенциала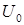 
на рёбрах или в вершинах модели. Значение 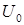на ребре может быть задано в виде линейной функции от координат. Параметры задающей линейной функции могут варьироваться от ребра к ребру, но должны быть подобраны так, чтобы избежать разрывов функции 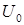в точках соприкосновения границ.
Замечание. Для того чтобы задача была сформулирована корректно, необходимо задание условия Дирихле хотя бы в одной точке расчетной области, а если область представляет собой набор физически не связанных подобластей - хотя бы в одной точке каждой такой подобласти. Это условие позволяет однозначно определить начальную точку отсчета потенциальной функции.
Условие Неймана – заданные значения нормальной составляющей плотности тока, определяются следующими соотношениями:
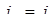- на внешней границе,
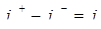- на внутренней границе,
где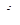 
- нормальная компонента вектора плотности тока, индексы "+" и "-" означают "слева от границы" и "справа от границы" соответственно, j в правой части выражений - плотность стороннего тока. Если 
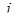= 0, граничное условие называется однородным. Однородное условие Неймана на внешней границе означает отсутствие нормальной составляющей напряженности и часто применяется для описания плоскости симметрии. Однородное условие Неймана является естественным, оно устанавливается по умолчанию, на всех тех рёбрах, составляющих внешнюю границу, где явно не указано иное граничное условие. Однородное граничное условие всегда имеет место на границе раздела диэлектрик – проводящая среда, где силовые линии вектора располагаются касательно к границе. При задании неоднородного условия Неймана на внешней границе, являющейся следом плоскости симметрии, истинную величину плотности тока следует разделить пополам.
Граничное условие равного потенциала используется для описания изолированных проводников, у которых проводимость материала значительно больше, чем проводимость окружающей среды. Это условие отличается от условия Дирихле тем, что значение потенциала на описываемой поверхности не известно заранее.
Замечание. Не допускается соприкосновение поверхностей, носящих граничное условие Дирихле и условие равного потенциала. В этом случае последнее условие следует описать с помощью условия Дирихле.
Вычисляемые физические величины в задачах растекания токов: При анализе результатов задачи растекания токов ELCUT позволяет оперировать со следующими локальными и интегральными физическими величинами.
Локальные величины:
· Скалярный электрический потенциал ;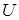
· Вектор напряженности электрического поля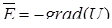 
, где
, 
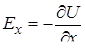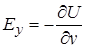- в плоском случае,
, 
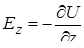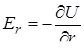- в осесимметричном случае;
· Вектор плотности тока:
.
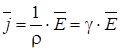Интегральные величины:
· Электрический ток через заданную поверхность:
,
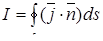где n - единичный вектор нормали к поверхности. Поверхность s может быть замкнутой или разомкнутой;
· Мощность тепловыделения в заданном объеме:
.
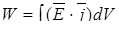В плоскопараллельной постановке интегральные характеристики вычисляются на единицу длины расчетной области в направлении оси z. Область интегрирования задается в плоскости модели замкнутым или разомкнутым контуром, состоящим из отрезков и дуг окружностей.
Специальные возможности: Интегральный калькулятор может вычислять различные интегральные значения на определенных пользователем линиях и поверхностях. Мощность тепловыделения может быть передана в качестве источника тепла в задачу расчета температурного поля (совмещенная электротепловая задача).
Примеры решения задач на растекание токов в ELCUT
Задача 1
Видоизменим условия задачи раздела 1.6 (рис. 3.1), имея в виду аналогию полей электростатики и стационарного поля постоянного тока (метод электростатической аналогии (см. раздел 6.2.2)). Положим, что один провод двухпроводной линии находится в проводящей среде с удельной проводимостью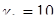 
(См/м), т.е. с удельным сопротивлением 
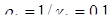(Ом×м), а второй - в проводящей среде с параметрами: 
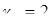(См/м) (или 
(Ом×м)); потенциалы проводов 
, 
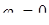кВ; геометрические параметры системы h = 0,5 м, d = 0,3 м; H = 0,65 м; радиус проводов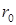 
= 10 мм. Если не указывать других граничных условий, то при обращении к ELCUT на всех рёбрах, ограничивающих область исследования поля, автоматически устанавливаются однородные граничные условия ( 
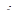= 0). Это будет означать, что область исследования поля окружена непроводящими границами, и силовые линии токов проводимости вблизи границ будут ориентироваться параллельно этим границам.
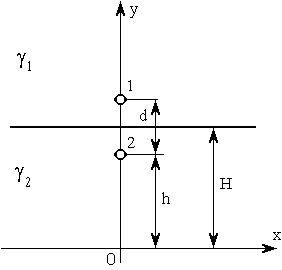
Рис. 3.1. Задача стационарного поля постоянного тока с двумя средами
Для того чтобы легко и быстро решить задачу в ELCUT, воспользуемся созданной в разделе 4 геометрической моделью.
1. Левой кнопкой мыши вызываем в ELCUT меню Файл, далее “Открыть”. В открывшемся окне выбираем в графе “Тип файлов” - Модели ELCUT (*.mod). Выбираем файл electro_01.mod, откроется его окно. Левой кнопкой мыши еще раз вызываем меню Файл, далее команду “Сохранить как…” и вводим новое имя модели electro_02.mod. Выбираем “Сохранить” и закрываем окно геометрической модели electro_02.
2. Следуем пункту 1.1 раздела 4.2, чтобы создать новую задачу ELCUT. При появлении окна “Создание задачи”, приглашающего ввести имя и расположение новой задачи (см. рис. 2.2), вводим в графе “Имя файла” имя новой задачи (electro_02). Нажимаем “Далее>”, чтобы продолжить диалог. При появлении окна “Ввод параметров новой задачи” (см. рис. 2.3), в графе тип задачи выбираем левой кнопкой мыши - “Электрическое поле постоянных токов”, класс модели - “Плоская”, расчет – “Обычный”. Принимаем предложенные системой имена файлов модели и физических свойств, следуем “Далее”. В появившемся окне “Выбор системы координат” (см. рис. 2.4), выбираем левой кнопкой мыши “Единицы длины” – сантиметры, “Система координат” – Декартовы координаты. Завершаем диалог – “Готово”.
3. Левой кнопкой мыши дважды щелкнем на элементе “Геометрия: electro_02.mod” “дерева” задачи, открывается окно геометрической модели. Перейдем в режим вставки, нажав клавишу Insert. Нажав правую кнопку мыши, выбираем из списка команд контекстного меню “Добавить вершины…” (см. рис. 2.8). В открывшемся окне (см. рис. 2.9) вводим с клавиатуры в соответствующих графах x и y координаты вершины (-100, 65), затем “Добавить”. Вводим координаты другой вершины (100, 65), далее “Добавить”, затем “Закрыть”. Соединяем созданные вершины ребром, которое представляет собой границу раздела сред (рис. 3.2). Отметим, что если геометрическая модель содержала расчетную сетку, то после создания новых объектов (вершин) она исчезнет.
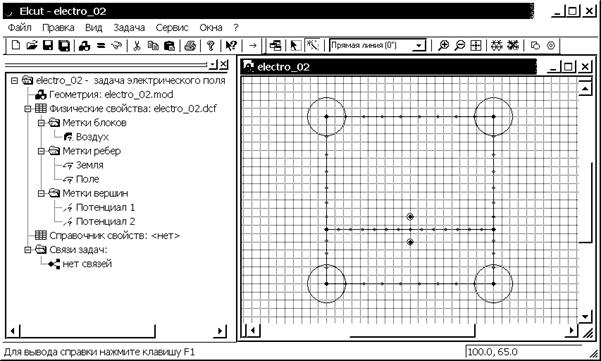
Рис. 3.2. Интерфейс задачи 1 с окном геометрической модели, включающей два блока расчетной области и электроды двухпроводной линии
4. В новой постановке имеем две среды, для каждой создаем метку – имена Среда 1, Среда 2. Перейдем в режим выделения, нажав клавишу Insert. В окне геометрической модели дважды щелкнем левой кнопкой мыши на блоке, где расположен верхний провод двухпроводной линии. В открывшемся окне “Свойства выделенных объектов” вместо имени “Воздух” вводим с клавиатуры в соответствующую графу название метки - Среда 1. Нажимаем “ОК”, чтобы закрыть окно. Аналогично присваиваем блоку, где расположен нижний провод двухпроводной линии, метку с именем - Среда 2.
Дважды щелкнем левой кнопкой мыши на нижнем ребре (в задаче раздела 2.2 ей соответствовала метка с именем “Земля”). В открывшемся окне “Свойства выделенных объектов” (см. рис. 2.18) выбираем левой кнопкой мыши в графе “Метка” из списка имен - “(нет)”, вместо имени “Земля”. Нажимаем “ОК”, чтобы закрыть окно. Аналогично поступаем с верхним ребром (в задаче раздела 2.2 ей соответствовала метка с именем “Поле”).
5. Зададим физические свойства сред. После двойного щелчка левой кнопки мыши на появившемся в “дереве” задачи элементе “Среда 1”, открывается окно “Свойства метки блока – Среда 1”. В графе “Удельное сопротивление” щелкнем левой кнопкой мыши на графе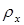 
и вводим с клавиатуры 0.1 (Ом×м). Так как пункт “Анизотропный проводник” не выбран, в графе 
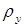автоматически появляется 0.1 (Ом×м). Оставляем систему координат – Декартову. Нажимаем “ОК”, чтобы закрыть окно.
Аналогично задаем для метки блока с именем “Среда 2” в окне “Свойства метки блока – Среда 2” величину 
равную 0.5 (Ом×м).
6. В данной постановке задачи определены потенциалы проводов – граничные условия Дирихле. После двойного щелчка левой кнопки мыши в “дереве” задачи на элементе “Потенциал 1”, в открывшемся окне “Свойства метки вершины – Потенциал 1” активируем графу “Потенциал” и оставляем в ней нуль. Нажимаем “ОК”, чтобы закрыть окно. Аналогично для элемента “Потенциал 2” в окне “Свойства метки вершины – Потенциал 2” активируем графу “Потенциал” и вводим с клавиатуры –10000 (В). Нажимаем “ОК”, чтобы закрыть окно. Задание граничных условий закончено.
7. Активируем окно геометрической модели и нажимаем кнопку 
“Построение сетки” на дополнительной панели инструментов модели или можно воспользоваться командой “Построить сетку” в списке команд меню Правка. В модели автоматически создается расчетная сетка (рис. 3.3).
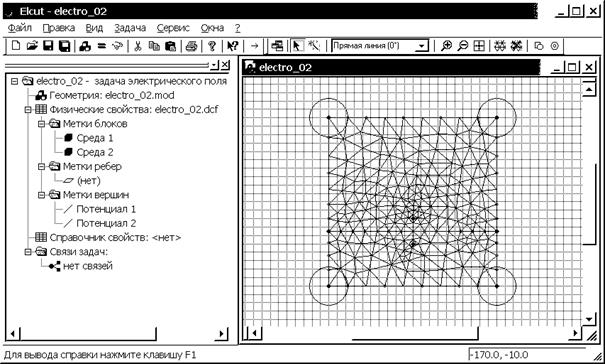
Рис. 3.3. “Дерево” задачи 1 и окно геометрической модели с автоматически построенной расчетной сеткой
Задача создана и ее следует сохранить (Ctrl+S).
8. Теперь можно решить задачу и посмотреть результаты решения. Для этого щелкнем левой кнопкой мыши на кнопке “Решить” 
или кнопке “Увидеть результат” 
общей панели инструментов. После утвердительных ответов на все информационные сообщения системы, когда решение закончится, автоматически откроется окно результатов решения, в котором будет отражена картина поля.
Выбираем левой кнопкой мыши в меню Вид команду “Картина поля”, после чего появляется соответствующее окно. Активизируем те параметры поля, которые необходимо отобразить. Так на рис. 3.4 отражены картина векторов напряженности и потенциальной функции. Видно, что на границе раздела двух проводящих сред нормальная составляющая напряженности поля испытывает скачок, меняясь обратно пропорционально проводимости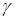 
соответствующих сред (см. 2.6 раздела 6.1.1).
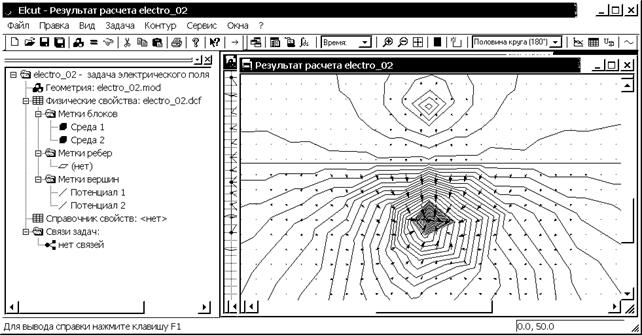
Рис. 3.4. Интерфейс задачи 1 с окном картины векторов напряженности и потенциальной функции
Картина плотности тока представлена на рис. 3.5, из которой видно, что на границе раздела двух проводящих сред нормальная составляющая меняется непрерывно без скачков (см. 6.2.5 раздела 6.2.1). На внешних границах вектор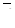 
направлен по касательной, что обусловлено однородными граничными условиями, которые устанавливаются в пакете по умолчанию.
Для получения интегральных характеристик необходимо задать в окне результатов расчета задачи контур. Например, используя координаты (0, 48) и (0, 52), создадим замкнутый контур вокруг нижнего электрода (рис. 3.6), при этом тип ребра контура - половина круга (180°). Для него получим ток растекания I = -2592.9 А (при направлении контура против часовой стрелки) или I = 2592.9 А (при смене направления контура по часовой стрелке), который определён внешним (сторонним) источником питания, при этом мощность тепловых потерь W = 2135200 Вт.
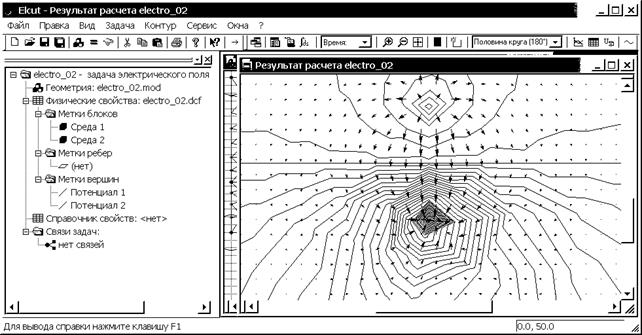
Рис. 3.5. Интерфейс задачи 1 с окном картины векторов плотности тока и потенциальной функции
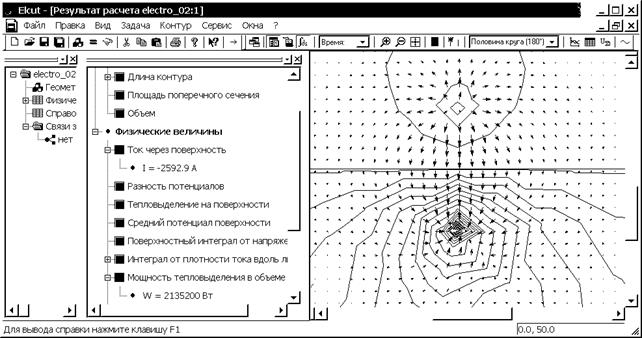
Рис. 3.6. Пример расчета интегральных характеристик для замкнутого контура вокруг нижнего электрода
Используя координаты (0, 78) и (0, 82), создадим замкнутый контур вокруг верхнего электрода, при этом тип ребра контура - половина круга (180°). Для него получим ток растекания I = 2705.1 А (при направлении контура против часовой стрелки), который является тем же током, который стекает с нижнего электрода. При этом расчетная погрешность между токами не велика даже при ограничении на число узлов расчетной сетки.
Создание разомкнутого (незамкнутого) контура в окне результатов расчета задачи позволяет определить ток, протекающий через разомкнутую (незамкнутую) поверхность 
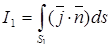
как часть полного тока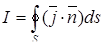 
, стекающего с электрода. Например, используя координаты точек: 1 - (5, 45) и 2 - (25, 20), создадим незамкнутый контур около нижнего электрода (рис. 3.7), при этом тип ребра контура – прямая линия (0°). Для него получим ток растекания 
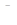= 441.42 А.
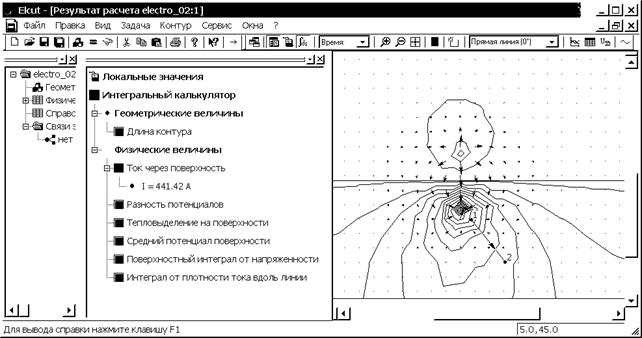
Рис. 3.7. Пример расчета интегральных характеристик для незамкнутого контура около нижнего электрода
Задача решена, её следует сохранить (Ctrl+S), после чего закрыть.
Задача 2
Рассмотрим в ELCUT решение задачи на растекание тока сферического заземлителя. Отметим еще раз, что в ELCUT осесимметричные задачи решаются в цилиндрической системе координат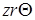 
, порядок следования осей выбран для общности с плоскопараллельными задачами. Физические свойства и источники поля предполагаются не зависящими от угловой координаты. Работа с моделью проводится в полуплоскости r ≥ 0. Ось вращения z направлена слева направо, ось r - снизу вверх.
Формулировка задачи повторяет задачу, рассмотренную в 
разделе 6.2.3. К сферическому заземлителю (электроду) радиуса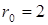 
м подводится ток I = 
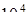А (рис. 2.1а). Заземлитель находится на расстоянии h = 6 м от границы раздела двух сред с разными удельными проводимостями 
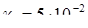(Cм/м), т.е. с удельным сопротивлением 
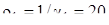(Ом×м), и 
(Cм/м), т.е. с удельным сопротивлением 
(Ом×м). Исследовать картину поля при условии равенства нулю потенциала в бесконечно удалённой точке.
1. Следуем пункту 1.1 раздела 2.2, чтобы создать новую задачу ELCUT. При появлении окна “Создание задачи”, приглашающего ввести имя и расположение новой задачи (см. рис. 2.2), вводим в графе “Имя файла” имя новой задачи (electro_03). Нажимаем “Далее>”, чтобы продолжить диалог. При появлении окна “Ввод параметров новой задачи” (см. рис. 2.3), в графе тип задачи выбираем левой кнопкой мыши - “Электрическое поле постоянных токов”, класс модели - “Осесимметричная”, расчет – “Обычный”. Принимаем предложенные системой имена файлов модели и физических свойств, следуем “Далее”. В появившемся окне “Выбор системы координат” (см. рис. 2.4) оставляем в графе “Единицы длины” – метры, “Система координат” – Декартовы координаты. Завершаем диалог – “Готово”.
2. Левой кнопкой мыши дважды щелкнем на элементе “Геометрия: electro_03.mod” “дерева” задачи. Появляется окно ELCUT (см. рис. 2.6). Выбираем левой кнопкой мыши пункт “ОК”.
Определимся с границами расчетной области. Так как по условию задачи максимальное расстояние 4 h = 24 м, выбираем границы 0 м £ z £ 48 м, 0 £ r £ 48 м. В дальнейшем все координаты в метрах.
Упростить в модели сферический заземлитель до точечного растекателя тока не представляется возможным, так как его геометрические размеры сопоставимы с размерами всей модели.
Создадим расчетную область, используя возможности надстройки “Вставка фигуры”. Для ее вызова следует нажать комбинацию клавиш Ctrl+Alt+S, можно также воспользоваться командой “Добавить Фигуру…” меню Правка или его контекстного меню. Открывается соответствующее окно надстройки. Выбираем во вкладке “Фигура” тип контура – прямоугольник (см. рис. 2.8). Щелкая левой кнопкой мыши в соответствующих графах окна, вводим с клавиатуры: длина w=24, высота h=48, центр в точке с координатами x=12, y=24, угол поворота вокруг оси = 0, далее выбираем “Добавить”. В окне геометрической модели при этом появляется соответствующий первой среде блок.
Для создания блока, соответствующего второй среде, щелкая левой кнопкой мыши в соответствующих графах окна “Добавить фигуру”, вводим с клавиатуры: длина w=24, высота h=48, центр в точке с координатами x=36, y=24, угол поворота вокруг оси = 0, далее выбираем “Добавить” и затем “Закрыть”.
Нажав кнопку “Показать все” на дополнительной панели инструментов модели, получим наиболее удобное отображение расчетной области, представляющей собой два прямоугольных блока с одним общим ребром, которое является границей раздела сред.
Картина поля симметрична относительно оси вращения z, что позволяет представить сферический заземлитель половиной окружности (работа с моделью проводится в полуплоскости r ≥ 0).
Для создания модели заземлителя переходим в режим вставки, нажав клавишу Insert. Далее щелкаем правой кнопкой мыши и выбираем из списка команд контекстного меню “Добавить вершины…”. В открывшемся окне “Добавление вершин” вводим с клавиатуры в соответствующих графах z и r координаты вершин заземлителя (16, 0), затем “Добавить” и (20, 0), затем “Добавить” и “Закрыть”. Соединяем созданные вершины заземлителя ребром с раствором дуги “Половина круга (180º)” из правой точки к левой. Если ELCUT после ввода ребра с круглым контуром автоматически видоизменит контур ребра на многогранный, то следуем рекомендациям пункта 1.4 раздела 2.2. Щелкнем левой кнопкой мыши на одной из вершин заземлителя, затем, удерживая клавишу Ctrl, на другой. Отпускаем клавишу Ctrl и нажимаем комбинацию клавиш Alt+Enter. В открывшемся окне “Свойства выделенных объектов” меняем автоматически заданный шаг дискретизации в вершинах ребра на заданный вручную, выбираем шаг дискретизации в вершинах заземлителя = 0.5 (м). Нажимаем “ОК”, чтобы закрыть окно.
Геометрическая модель создана (рис. 3.8), и её следует сохранить (Ctrl+S).
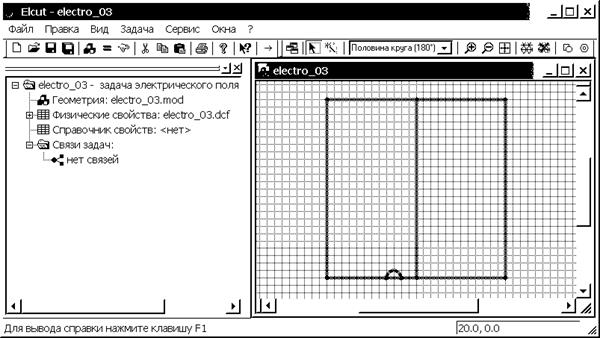
Рис. 3.8. Интерфейс задачи 2 с окном геометрической модели, включающей две среды и заземлитель
Замечание. Отметим, что для правильного описания и решения задач в осесимметричной постановке необходимо хорошо представлять, проекциями объектов какой формы являются создаваемые кривые. Если создать окружность в поле геометрической модели выше оси z, то она будет являться проекцией тора. Если же провести прямую, параллельную оси z, то при ее вращении вокруг оси z в пространстве описывается цилиндр.
3. В задаче имеется две среды, для каждой необходимо создать метку. В режиме выделения объектов дважды щелкнем левой кнопкой мыши в окне геометрической модели на блоке соответствующем первой среде. В открывшемся окне “Свойства выделенных объектов” вводим с клавиатуры в соответствующую графу название метки - Среда 1. Нажимаем “ОК”, чтобы закрыть окно. Аналогично присваиваем блоку соответствующему второй среде метку с именем - Среда 2. Для области внутри заземлителя создавать метку не нужно, так как поле внутри его не рассматривается.
Дважды щелкнем левой кнопкой мыши на ребре заземлителя полукруглой формы. В открывшемся окне “Свойства выделенных объектов” вводим с клавиатуры в соответствующую графу название метки - Заземлитель. Нажимаем “ОК”, чтобы закрыть окно.
Выделим верхние ребра модели, для чего щелкнем левой кнопкой мыши на одном из верхних ребер, затем, удерживая клавишу Ctrl, на другом. Отпускаем клавишу Ctrl и нажимаем комбинацию клавиш Alt+Enter или, нажав правую кнопку мыши, выбираем из списка команд контекстного меню команду “Свойства”. В открывшемся окне “Свойства выделенных объектов” вводим с клавиатуры в соответствующую графу название метки - Ноль. Нажимаем “ОК”, чтобы закрыть окно.
4. Зададим физические свойства сред. После двойного щелчка левой кнопки мыши на появившемся в “дереве” задачи элементе “Среда 1”, открывается окно “Свойства метки блока – Среда 1”. В разделе “Удельное сопротивление” щелкнем левой кнопкой мыши на графе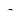 
и вводим с клавиатуры 20 (Ом×м). Так как пункт “Анизотропный проводник” не выбран, в графе 
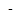автоматически появляется 20 (Ом×м). Оставляем систему координат – Декартову. Нажимаем “ОК”, чтобы закрыть окно.
Аналогично задаем для метки с именем “Среда 2” в окне “Свойства метки блока – Среда 2” величину 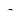равную 100 (Ом×м) (рис. 3.9).
5. В данной задаче – задано граничное условие Неймана. После двойного щелчка левой кнопки мыши в “дереве” задачи на элементе “Заземлитель”, в открывшемся окне “Свойства метки ребра – Заземлитель” активируем графу “Нормальная плотность тока”. Величину поверхностной плотности тока, которую необходимо задать, определяем по формуле:
( 
)
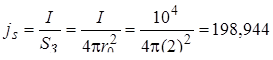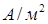Вводим найденную величину плотности тока и нажимаем “ОК”, чтобы закрыть окно (рис. 3.10).
Рис. 3.9. Интерфейс задачи 2 и окно физических свойств блока с меткой Среда 2
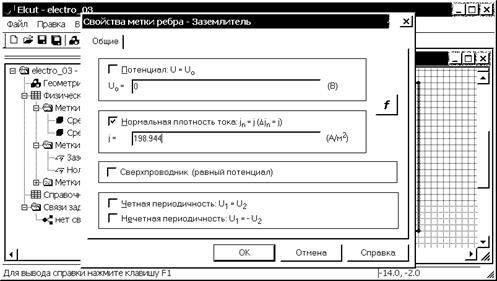
Рис. 3.10. Интерфейс задачи 2 и окно задания граничного условия Неймана на ребре с меткой Заземлитель
Для того чтобы задача была сформулирована корректно, необходимо задание условия Дирихле хотя бы в одной точке расчетной области. Зададим условие Дирихле на самых удаленных ребрах модели – верхних и определим на них потенциал равным нулю. После двойного щелчка левой кнопки мыши в “дереве” задачи на элементе “Ноль”, в открывшемся окне “Свойства метки ребра – Ноль” активируем графу “Потенциал” и оставляем в ней нуль. Нажимаем “ОК”, чтобы закрыть окно.
На остальных ребрах модели автоматически устанавливаются однородные граничные условия ( 
= 0).
6. Активируем окно геометрической модели. Для повышения точности расчета следует воспользоваться рекомендациями раздела 2.2 пункт 7 и задавать шаги дискретизации в вершинах модели вручную. Выделяем, удерживая Ctrl, четыре вершины в углах расчетной области и верхнюю вершину на ребре границы раздела сред. Отпускаем клавишу Ctrl и нажимаем комбинацию клавиш Alt+Enter. В открывшемся окне “Свойства выделенных объектов” меняем автоматически заданный шаг дискретизации на заданный вручную = 5 (м). Нажимаем “ОК”, чтобы закрыть окно.
Щелкнем левой кнопкой мыши на нижней вершине ребра границы раздела сред и нажимаем комбинацию клавиш Alt+Enter. В открывшемся окне “Свойства выделенных объектов” меняем автоматически заданный шаг дискретизации на заданный вручную = 2 (м). Нажимаем “ОК”, чтобы закрыть окно.
Нажимаем кнопку “Построение сетки” на дополнительной панели инструментов модели или можно воспользоваться командой “Построить сетку” в списке команд меню Правка. В модели автоматически создается расчетная сетка (рис. 3.11).
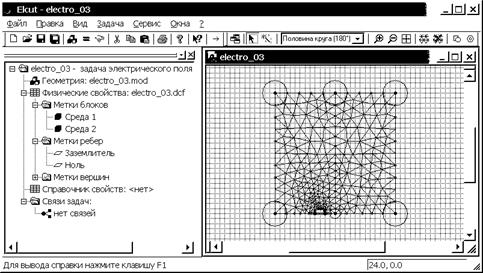
Рис. 3.11. “Дерево” задачи 2 и окно геометрической модели с автоматически построенной расчетной сеткой
Вызов окна “Свойства выделенных объектов” осуществляется нажатием комбинации клавиш Alt+Enter и показывает число созданных узлов. При установленных выше в режиме “Задан” шагах дискретизации общее число узловых точек сетки будет равно 254.
Задача создана и ее следует сохранить (Ctrl+S).
7. Теперь можно решить задачу и посмотреть результаты решения. Для этого щелкнем левой кнопкой мыши на кнопке “Решить” или кнопке “Увидеть результат” общей панели инструментов. После утвердительных ответов на все информационные сообщения системы, когда решение закончится, автоматически откроется окно результатов решения, в котором будет отражена картина поля. Используя команду “Картина поля…” меню Вид, вызываем соответствующее окно “Картина поля” и выбираем параметры поля, которые необходимо отобразить (рис. 3.12).
Рис. 3.12. Интерфейс задачи 2 с окном результатов расчета картины поля
Построим график изменения потенциала при r = 0 вдоль оси z. Для точного задания начала и конца линии построения, щелкнув правой кнопкой мыши в окне результатов расчета, выбираем из контекстного меню команду “Ввод линий контура…”. Открывается окно “Добавление линий”. Первая точка имеет координаты (0, 0), щелкнем левой кнопкой мыши на пункт “Начальная точка”. Пункт “Начальная точка” сменяется пунктом “Добавить линию”. Вводим с клавиатуры координаты второй точки (48, 0) в соответствующих графах, при этом тип контура линии – прямая линия (0°), и нажимаем левой кнопкой мыши на пункт “Добавить линию”. Выбираем “Закрыть”, чтобы завершить диалог.
При создании линии или контура автоматически активизируются кнопки “График” и “Таблица” панели анализа результатов 
. Нажатие левой кнопкой мыши на любой из них вызывает соответствующее окно. График изменения потенциала при r = 0 вдоль оси z представлен на рис. 3.13. Помимо потенциальной функции можно вывести графики изменения других параметров поля вдоль выбранной линии, например, компоненты напряженности (рис. 3.14).
Сравнивая рисунки 5.13 и 2.2, 5.14 и 2.6 можно судить о хорошем совпадении результатов даже при ограничении на число узлов. Отметим, что относительная погрешность расчета в ELCUT определяется границей расчетной области и числом узлов расчетной сетки и возрастает в областях с малым числом узлов.
Плотность тока проводимости определяет в каждом элементарном объеме мощность тепловых потерь. На рис. 3.15 выведен график тепловых потерь вдоль оси z при r = 0. Аналогичные графики могут быть выведены и по другим линиям, например, на границе раздела сред.
Решение задачи окончено, её следует сохранить (Ctrl+S) и закрыть. По команде “Выход” меню Файл пакет ELCUT автоматически закрывается.
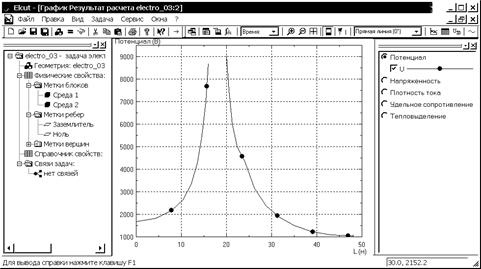
Рис. 3.13. График изменения потенциала при r = 0 вдоль оси z
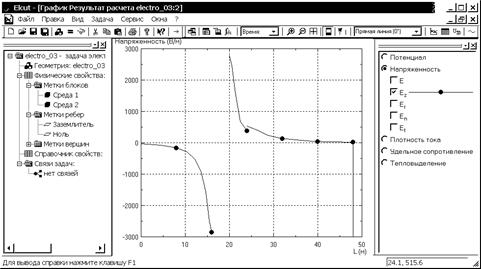
Рис. 5.14. График изменения z-компоненты напряженности вдоль оси z при r = 0
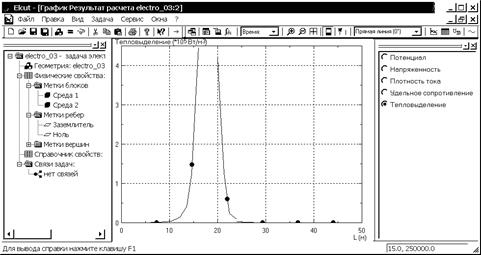
Рис. 3.15. График тепловых потерь вдоль оси z при r = 0.
ТЕМА 3
Графы
Графы широко используются в различных областях науки и техники для моделирования отношений между объектами. На макроуровне графы применяются для графического изображения топологических уравнений.
Считается, что теория графов зародилась в XVIII столетии в г. Кенигсберге (ныне г. Калининград), жители которого пытались решить задачу о переходе мостов города (река Прегель) по такому маршруту, в котором бы были пройдены все мосты, но каждый мост был пройден только один раз (рис. 3.1, а). Эту задачу удалось решить Эйлеру. Он показал, каким условиям должен удовлетворять граф, полученный по схеме мостов, (рис.3.1, б), чтобы такая задача имела решение.
Рис. 1.1. Схема мостов (а) и граф маршрутов (б)
Графом называется совокупность вершин (узлов) и связанных с ними ребер (ветвей). Граф можно задать в виде G = <V, E>, где V – множество вершин; E – отношение на V(E Ì V ´ V) – множество ребер. На рис. 3.2, а показан граф G, в котором множество ребер E есть {a, b, c, d, e, f, g}, а множество вершин V = {1, 2, 3, 4, 5}.
Подграфом называют такую часть графа, которая включает в себя некоторые вершины и ребра графа, причем среди ребер могут быть только те, которые связывают вершины подграфа. На рис. 3.2, б показан подграф G' графа G.
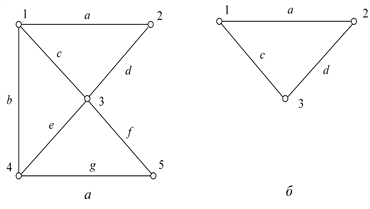
Рис. 3.2. Граф G (а) и его подграф G' (б)
Направленный (ориентированный) граф имеет ребра, на которых указаны направления. Ребра направленного графа называют дугами. На рис. 3.3, а показан ориентированный граф.
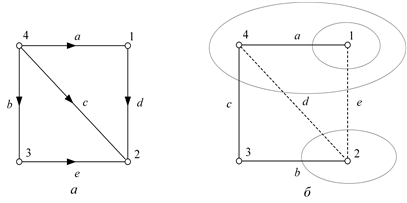
Рис. 3.3. Ориентированный граф (а), сечения дерева графа (б)
Степенью вершины Vi графа называют число ребер, инцидентных этой вершине. Термин «инцидентность» означает отношение объектов типа «проходят через…», «соединены с…». Две вершины называют смежными, если они соединены ребром. Например, на рис. 3.3, а вершина 4 смежна с вершиной 2, так как они соединены посредством ребра с.
Граничные вершины ребра – вершины, инцидентные этому ребру.
Кратные ребра – ребра с одинаковыми граничными вершинами.
Маршрутом (путем) S называют любую последовательность ребер, в которой соседние ребра инцидентны одной и той же вершине. В графе на рис. 3.2, а последовательности (a, d, e, g) и (b, g) – маршруты, а последовательность (d, g) маршрутом не является, так как ребра d и g инцидентны разным вершинам. Если в маршруте нет повторяющихся ребер, то он называется цепью. Если цепь начинается и кончается в одной и той же вершине, то она называется циклом-контуром. Количество ребер в S называют длиной маршрута.
Если каждому ребру графа приписано какое-то число (вес), то граф называют взвешенным.
Связным называют граф, в котором можно указать маршрут, связывающий любые вершины.
В задаче о кенигсбергских мостах (см. рис. 3.1) Эйлер показал, что такой граф не представляет собой единого цикла; иными словами, с какой бы вершины мы ни начали обход, мы не сможем обойти весь граф и вернуться обратно, не проходя никакого ребра дважды. Если бы такой цикл существовал, то, выйдя из начальной вершины, нужно было туда вернуться, а для всех промежуточных вершин нужно в них войти и выйти – степени всех вершин должны быть четными числами. Это условие не выполняется для кенигсбергских мостов.
Если на графе можно найти цикл, содержащий все его ребра, причем каждое ребро в точности по одному разу, то такой цикл называется эйлеровой линией, а граф, обладающий эйлеровой линией, – эйлеровым графом.
Если необходимо найти путь S в связанном графе, содержащий все его ребра по одному разу, в котором начальная и конечная вершины не совпадают, необходимо и достаточно, чтобы начальная и конечная вершины были единственными вершинами с нечетными степенями.
Деревом связного графа называют наименьший связный подграф данного графа.
Ветвями дерева называют ребра графа, вошедшие в дерево, а хордами – ребра графа, не вошедшие в дерево. Для одного и того же графа в общем случае можно указать несколько деревьев.
Контуром k-й хорды называют множество ребер, образующих цикл в графе, который получается при добавлении k-й хорды к дереву.
Сечением ветви дерева называют множество ребер, пересекаемых линией сечения, если:
а) среди ветвей дерева пересекается единственная;
б) линия сечения замкнутая и любое ребро может пересекаться не более одного раза.
Для графа, показанного на рис. 3.3, б, сечения ветвей его дерева записываются: a – (a, e); b – (b, d, e); c – (c, d, e).
Графы можно представить с помощью различных матриц, что является удобным при использовании алгебраических методов решения многих задач теории графов. Наиболее важными матричными представлениями являются матрицы инциденций (соединений) и смежности.
Первая матрица инциденций M для неориентированного графа представляет собой матрицу, строки которой соответствуют вершинам, а столбцы – ребрам. Элемент матрицы равен единице, если вершина инцидентна ребру. В противном случае элемент матрицы принимает значение ноль.
Для ориентированного графа элемент матрицы инциденций M равен +1, если вершина, инцидентная дуге, является начальной вершиной дуги (т. е. дуга исходит из этой вершины). Элемент равен –1, когда дуга входит в вершину. Если вершина не инцидентна дуге, то элемент матрицы равен 0. Так, для графа на рис. 3.3, а матрица M имеет следующий вид:
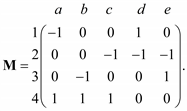(3.1)
В каждом столбце матрицы M находится две единицы – одна положительная, а другая отрицательная, так как каждое ребро инцидентно только двум вершинам. В каждой строке имеется столько единиц, сколько ребер инцидентно соответствующей вершине.
Вторая матрица инциденций N устанавливает соответствие между ребрами графа и независимыми контурами графа. В зависимости от выбранной системы независимых контуров – дерева графа можно составить разные матрицы N. Число независимых контуров обозначают через k. Каждой строке матрицы N ставят в соответствие контур, таким образом, число строк в матрице N равно числу независимых контуров k; каждому столбцу матрицы N ставят в соответствие ребро, и число столбцов матрицы N равно числу ребер – m.
Матрица N составляется по следующим правилам. Независимые контуры нумеруют от 1 до k; выбирают направления обхода контуров; начиная с первого выполняют обход контуров в соответствии с выбранными направлениями; проверяют, совпадает ли направление очередного ребра с направлением обхода контура: если да, то в соответствующем столбце матрицы N ставится +1, в противном случае –1; для ребер, не вошедших в рассматриваемый контур, в соответствующие столбцы проставляют нули.
Так, если в качестве дерева графа на рис. 3.3, а взять подграф с ребрами (a, b, c), то при добавлении хорды d образуется контур (a, d, c), а при добавлении хорды e – контур (c, e, b). Для такой системы независимых контуров матрица N имеет вид:
. (3.2)
Матрица смежности A является квадратной матрицей и для невзвешенного графа состоит из нулей и единиц: Ai,j= 1, если (i, j ) Î E, и Ai,j = 0 в противном случае. Для взвешенного графа Ai,j равно весу соответствующего ребра, а отсутствие ребра в ряде задач удобно обозначать бесконечностью. Если граф ориентированный, то для каждого ребра ставится Ai,j = 1, если направление от i к j, а Aj,i = – 1 и наоборот. Для неориентированных графов матрица смежности всегда симметрична относительно главной диагонали. Для графа на рис 2.14, а матрица A имеет следующий вид:
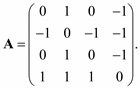(3.3)
С помощью матриц M и A легко проверить, существует ли в графе ребро, соединяющее вершину i с вершиной j. Основной недостаток этих матриц заключается в том, что они требуют, чтобы объем памяти был достаточен для хранения соответственно nm и n2 значений.
Этого недостатка лишены такие способы хранения графа, как одномерный массив длины n списков или множеств вершин. В таком массиве каждый элемент соответствует одной из вершин и содержит список или множество вершин, смежных с ней.
Для реализации некоторых алгоритмов более удобным является описание графа перечислением его ребер. В этом случае его можно хранить в двумерном массиве из двух строк и длиной m, каждый столбец которого содержит номер начальной вершины и номер конечной вершины графа.
При работе с графами на компьютере удобно вершины графа сопоставлять с числами от 1 до n, где n = |V| – количество вершин графа, и рассматривать V = {1, 2, … n}. Ребра нумеруют числами от 1 до m, где m = |E|. В дальнейшем ребра будем именовать не буквами, а цифрами.
Дата: 2019-07-30, просмотров: 288.
