Расчеты режимов сложных схем электрических сетей требуют специальных моделей представления схем и компактной записи уравнений. Такими моделями являются графы и матрицы.
Линии, трансформаторы и другие элементы электрической сети представляются в расчетах своими схемами замещения, состоящими из ветвей с сопротивлениями и проводимостями. Все шины электрических станций и подстанций являются узловыми точками сети. Количество этих узловых точек или узлов схемы сети обозначим буквой n, а количество ветвей, соединяющих эти шины, m. Если сеть не содержит замкнутых контуров, то количество узлов и ветвей различается на 1: n = m + 1. При наличии контуров n = m + 1 – k, где k – количество независимых контуров.
Графы являются топологическими моделями схем электрических цепей.
По сути, изображение электрической схемы в виде графа повторяет графическое изображение схемы, но без элементов, из которых состоит электрическая цепь. Узлы (вершины графа) соединяются непрерывными линиями (ребрами), на которых при необходимости указывается положительное направление тока или потока мощности.
Элементами ЭЭС, которые моделируются ребрами графа, являются ЛЭП, трансформаторы, реакторы, батареи конденсаторов и др. Как правило, все они представляются П-образными схемами замещения и поэтому имеют элемент связи между двумя граничными узлами – продольная ветвь, и элементы, связывающие узлы с нейтральной точкой системы N, – поперечные ветви (рис. 3.4).
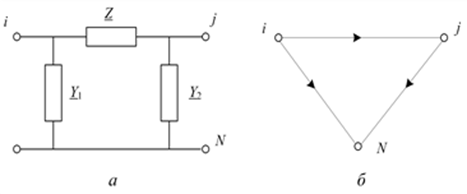
Рис. 3.4. П-образная схема замещения (а) и ее граф (б)
Для ЛЭП:
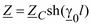, (3.4)
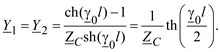(3.5)
Обычно Z = (r0 + jx0)l и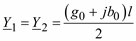 
.
Для трансформатора:
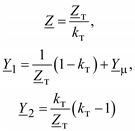(3.6)
при kт > 1. Если kт = 1, то из (3.6) получается Г-образная схема замещения трансформатора.
Для реакторов и батарей конденсаторов, включенных в виде продольных элементов сети, параметры схемы замещения: Z = jXр и Z = jXc. Y1 = Y2 = 0 (Y1 или Y2 может быть отлично от нуля и моделировать потери активной мощности в реакторе или батарее конденсаторов). В случае их включения в виде поперечных ветвей: Z = 0, а Y1 и Y2 представляются одной поперечной ветвью – Y шунта: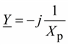 
и 
. Аналогично могут представляться своими схемами замещения электрические нагрузки .
Рассмотрим пример схемы электрической сети, состоящей из ЛЭП и трансформатора (рис. 3.5, а). Ее схема замещения есть две соединенные между собой П-образные схемы замещения – ЛЭП и трансформатора, а граф будет состоять из двух графов П-образных схем (рис. 3.5, б).
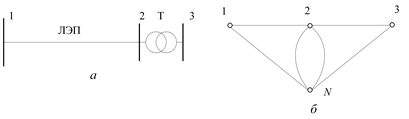
Рис. 3.5. Схема простой электрической сети (а) и ее граф (б)
Для более сложных схем, например, схемы на рис. 3.6, а, удобно ввести в рассмотрение нейтральную плоскость в сети и рассматривать узлы графа сети «висящими» над нейтральной плоскостью N и соединенными с ней поперечными ветвями (рис. 3.6, б).
Так как в общем случае каждая вершина графа инцидентна хотя бы одному ребру, связанному с вершиной (плоскостью) N, то при изображении графа эти ребра не изображаются (рис. 3.7).
Для моделирования топологии схем электрических сетей используют матричные модели, отражающие свойства графов. Это матрицы инциденций и смежности. В практических расчетах более удобной является компактная форма записи, например в виде перечисления ребер графа. Так, для графа рис. 3.7 массив имен ребер L может быть записан в следующем виде:
(3.7)
В первой строке массива L указывается номер (имя) начального узла, а во второй того же столбца – номер (имя) конечного узла. Пара номеров узлов в столбце образует имя ветви, например, для ветви b это 2 – 3.
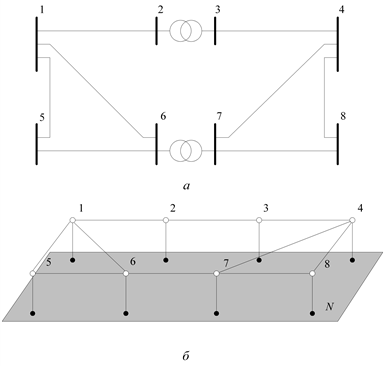
Рис. 3.6. Схема электрической сети из восьми узлов и десяти ветвей (а) и ее граф (б)
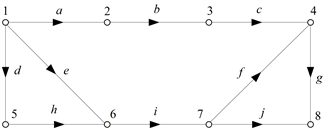
Рис. 3.7. Граф сети без изображения ребер, связанных с нейтральной плоскостью
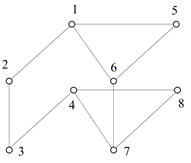
Рис. 3.8. Многослойный граф
В некоторых случаях можно использовать многослойные графы, в которых сеть каждого напряжения располагается в отдельном слое. Получается, что в горизонтальных слоях находятся ветви, моделирующие линии электропередачи, а между ними вертикально изображаются трансформаторные связи (рис. 3.8). Таких слоев может быть столько, сколько ступеней номинального напряжения имеется в сети.
Каждая продольная ветвь в графе электрической сети характеризуется сопротивлением Zj = Rj + jXj, а поперечная ветвь – проводимостью Yi = Gi + jBi (j = 1, 2,…, m; i = 1, 2,…, n), которые образуют матрицы параметров электрической сети – матрицу сопротивлений продольных ветвей и матрицу-столбец проводимостей поперечных ветвей – шунтов:
(3.8)
Здесь Zвjj = Zj, а YNi = Yi . Недиагональные элементы матрицы Zв обычно равны нулю, хотя в некоторых случаях учитывают взаимные сопротивления ветвей, которые могут быть отличны от нуля, например для близко расположенных ЛЭП возможно наличие взаимной индукции.
Кроме пассивных ветвей в сети существуют активные ветви, включающие источники ЭДС и тока. Эти ветви, как правило, являются поперечными и моделируют генераторы электрических станций (ЭДС) и потребителей электрической энергии (источники тока), – рис. 3.9, а.
(3.9)
Ветвь с ЭДС в действительности содержит еще и сопротивление и по сути является источником напряжения, которое зависит от нагрузки. В установившемся режиме достигается постоянство значения напряжения генераторов электростанций посредством специальных устройств регулирования и можно пренебречь влиянием сопротивлений генераторов на их напряжение. В дальнейшем будем считать эти ветви источниками ЭДС.
Принято не изображать на графе сети не только шунтирующие проводимости, но и активные поперечные ветви с ЭДС и источником тока, однако источник тока все же задают упрощенным изображением в виде стрелочки, направленной в узел (рис. 3.9, б). Это показывает, что в сеть «вливается» извне ток генерации или нагрузки (с обратным знаком). Такие токи называются токами инъекции (injection current) или задающими токами.
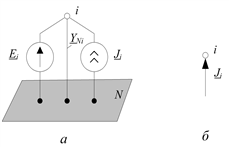
Рис. 3.9. Изображения поперечных ветвей
Матрицы E и J задают режим работы электрической сети и являются векторами независимых переменных. Они относятся к режимным параметрам электрической сети. Другие режимные параметры называются зависимыми переменными. К ним относятся напряжения в узлах, токи и напряжения в продольных ветвях и ряд других параметров режима:
U – матрица напряжений в узлах (узловые напряжения);
I – матрица токов ветвей;
U – матрица напряжений в ветвях (падения напряжения на сопротивлениях ветвей);
Sв(н) – матрица потоков мощности в начале ветвей;
Sв(к) – матрица потоков мощности в конце ветвей;
Sв – матрица потерь мощности в ветвях.
Рассмотрим пример направленного графа электрической сети, изображенного на рис. 3.10.
Для удобства записи в матричной форме параметров ветвей присвоим каждой ветви ее порядковый номер (на рис. 3.10 курсив). Составим матрицу соединений M для этого графа:
(3.10)
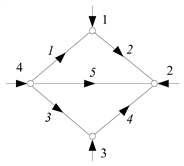
Рис. 3.10. Пример графа электрической сети
Умножим эту матрицу на матрицу токов ветвей, будем иметь:
(3.11)
Полученное соотношение является первым законом Кирхгофа в матричной форме записи
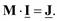(3.12)
Так как к узлам графа электрической сети еще присоединены другие поперечные ветви с ЭДС и проводимостью шунта, то задающий ток в (3.12) включает в себя также токи данных ветвей
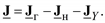(3.13)
Здесь: Jг – матрица токов генерации (ветви с ЭДС), которые определяются через мощности генерации;
Jн – матрица токов нагрузки, которые определяются через мощности нагрузки (имеет обратное направление – от узла);
JY – матрица токов в проводимостях шунтов, которые зависят от проводимости шунта из матрицы YN и напряжения в узле из матрицы U (также имеет обратное направление – от узла, так как моделирует потребление мощности).
Умножим транспонированную матрицу соединений МT на матрицу узловых напряжений, получим:
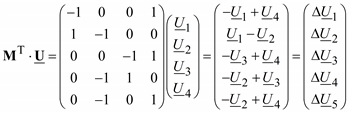(3.14)
или
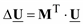. (3.15)
По закону Ома в матричной форме записи имеем
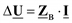(3.16)
или
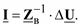(3.17)
Подставим в (3.12) выражение для матрицы токов ветвей (3.17) и затем (3.15), получим
(3.18)
Введем обозначение
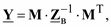(3.19)
тогда (3.18) приобретет вид
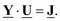(3.20)
Полученное соотношение является уравнением узловых напряжений (потенциалов) в матричной форме записи. Матрицу Y называют матрицей узловых проводимостей электрической сети. Рассмотрим структуру этой матрицы, для чего выполним матричные перемножения в (3.19). Заметим, что обратная матрица сопротивлений ветвей легко получается в силу своего диагонального вида – ее элементы суть обратные величины к сопротивлениям ветвей и являются проводимостями продольных ветвей.
Вначале перемножим первые две матрицы матричного произведения (3.19):
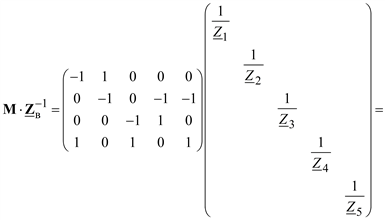
. (3.21)
Полученную матрицу умножим справа на матрицу MT. В результате получим:
(3.22)
Из полученной матрицы можно сделать следующие выводы о вычислении ее элементов.
1. Элементы, расположенные на главной диагонали матрицы, вычисляются как сумма проводимостей ветвей, подходящих к соответствующему узлу:
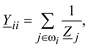(3.23)
где Yii – диагональный элемент матрицы Y;
Zj – сопротивление j-й ветви;
wi – множество номеров узлов, связанных с i-м узлом.
2. Недиагональные элементы равны проводимостям ветвей, имя каждой из которых состоит из номеров узлов, соответствующих номеру строки и номеру столбца, на пересечении которых находится данный элемент, и взятых с противоположным знаком. Матрица Y является симметричной матрицей.
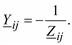(3.24)
Запишем уравнение узловых напряжений для узла с номером i:
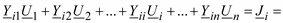
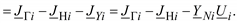(3.25)
Объединив подобные члены, получим, что в диагональные элементы матрицы Y войдут дополнительные слагаемые YNi:
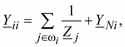(3.26)
т. е. диагональный элемент будет равен сумме проводимостей всех подходящих к i-му узлу ветвей, включая поперечную ветвь – шунт YNi.
Задающие токи узлов в (3.20) будут состоять только из токов генерации и токов нагрузки.
В случае отсутствия связей с нейтральной плоскостью N система уравнений (3.20) не имеет единственного решения, так как в этом случае определитель матрицы Y равен нулю. Сумма всех задающих токов в такой сети равна нулю:
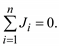(3.27)
Следовательно, среди всех n узлов можно выделить узел, например с номером n, ток в котором равен
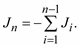(3.28)
Для уравнений узловых напряжений это означает, что одно уравнение лишнее, т. е. зависит от остальных уравнений и может быть получено через сумму всех остальных уравнений. Так как ток в этом узле может быть получен из баланса токов в сети (3.28), то его называют балансирующим. Обычно это шины мощной электростанции или системы.
Таким образом, из системы (2.20) исключается одно уравнение и тогда получается система независимых линейных уравнений порядка n – 1. Однако, поскольку число неизвестных напряжений по-прежнему равно n, в одном из узлов следует задать напряжение по величине и фазе так, чтобы все напряжения вычислялись относительно этого известного напряжения. Такой узел в сети называется базисным. Обычно фазу напряжения базисного узла принимают равной нулю, т. е. вектор напряжения базисного узла совмещают с действительной осью. Остальные узлы называют независимыми узлами.
Во многих случаях балансирующий узел и базисный узел совмещают, и в дальнейшем будем считать, что это один и тот же узел.
Таким образом, с исключением уравнения для базисного балансирующего узла с номером n будем иметь систему уравнений (3.20) с числом уравнений n – 1, однако в эти уравнения будет входить слагаемое с заданным напряжением базисного узла.
Изменим номер базисного балансирующего узла. Пусть его номер есть 0 (ноль). Тогда уравнение (3.20) приобретет следующий вид:
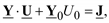(3.29)
где Y0 – матрица проводимостей ветвей, связывающих независимые узлы с базисным балансирующим узлом;
U0 – напряжение базисного узла (скаляр).
Матрица узловых проводимостей в (3.29) имеет порядок n – 1 и определяется через матрицу инциденций M, в которой нет одной строки, соответствующей балансирующему узлу.
Необходимо заметить, что во всех уравнениях, где одновременно присутствуют токи и напряжения (3.16), (3.17), (3.18), (3.20), (3.25) и (3.29), напряжения даны в фазных значениях, хотя индекс (буква «ф») для простоты не записывался. Эти же уравнения можно считать записанными и для линейных напряжений, однако токи будут увеличенными в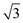 
раз, и для вычисления истинных токов их следует уменьшать в .
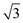Известными независимыми переменными в уравнениях установившегося режима могут быть задающие токи узлов и напряжение базисного узла. В этом случае решение уравнения (3.29) может быть записано в виде
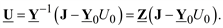(3.30)
Здесь Z – матрица узловых сопротивлений.
Численное решение системы уравнений (3.29) выполняется методом Гаусса или другим методом решения системы линейных алгебраических уравнений.
В случае, когда известны мощности в узлах сети – задающие мощности Si, токи можно вычислить приближенно через номинальные напряжения 
(i = 1,…, n – 1). Задающие мощности так же, как и токи, складываются из мощности генерации и мощности нагрузки:
(3.31)
Другой приближенный подход связан с представлением задающих токов через напряжения и проводимости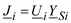 
, где YSi – проводимость генерации и/или нагрузки (схема замещения). Для i-го узла имеем:
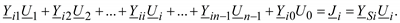(3.32)
Объединив подобные члены, получим
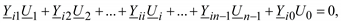(3.33)
где в элемент Yii входит проводимость YSi. Знак перед этой проводимостью зависит от того, какая мощность преобладает в узле: плюс, если нагрузка, и минус, если генерация. В матричной форме записи:
(3.34)
Решение матричного уравнения (3.34) запишется в виде
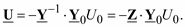(3.35)
Комплексную матрицу узловых проводимостей Y иногда представляют в блочной форме через ее вещественную G и мнимую B составляющие, и тогда система уравнений (3.34) становится системой с вещественными величинами:
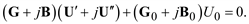(3.36)
После перемножения двучленов в (3.35) будем иметь:
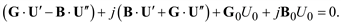(3.37)
Приравняем отдельно вещественные и мнимые части полученного уравнения и получим два матричных уравнения с вещественными величинами:
(3.38)
или в компактной форме записи:
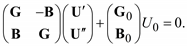(3.39)
Решение (3.39) запишется в виде
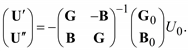(3.40)
Нелинейные модели
Так как во многих случаях расчеты ведутся при заданных мощностях нагрузок и генерации, то их следует ввести в уравнения установившегося режима.
Мощность в трехфазной сети в симметричных режимах выражается суммарной мощностью всех трех фаз:
(3.41)
В матричной форме это выражение можно записать, используя операцию диагонализации матрицы U. Матрица diag{U} есть квадратная матрица, в которой элементы матрицы U расположены по главной диагонали, а все остальные элементы равны нулю. Тогда
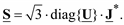(3.42)
Уравнение установившегося режима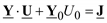 
записано для фазных токов и напряжений. Умножим обе части этого уравнения на 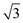и применим к величинам этого уравнения операцию сопряжения, получим
(3.43)
В левой части этого уравнения после умножения на 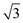напряжения стали линейными.
Умножим левую и правую части уравнения (3.43) слева на матрицу diag{U}, получим
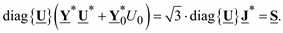(3.44)
Система уравнений (3.44) является системой нелинейных уравнений установившегося режима. В зависимости от формы представления комплексных величин применяют две основные формы этой системы уравнений.
Вначале рассмотрим алгебраическую форму записи. Для i-го узла имеем:
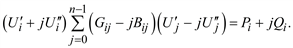(3.45)
После перемножения двучленов и разделения уравнения на два уравнения с вещественными величинами получим систему 2(n – 1) алгебраических уравнений
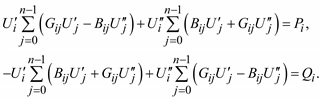(3.46)
Здесь i = 1,…, n – 1.
Тригонометрическая форма нелинейных уравнений установившегося режима может быть получена, если комплексные величины в уравнении (3.44) записать в виде
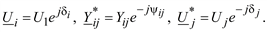(3.47)
Тогда
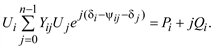(3.48)
Уравнение (3.48) в тригонометрической форме запишется как
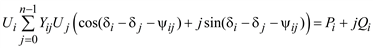, (3.49)
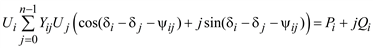, (3.50)
и после разделения на два вещественных уравнения
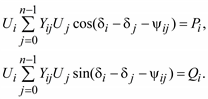(3.51)
Обычно вместо угла yij используют дополняющий до 90° угол αij. αij = 90 - yij, yij = 90 - αij.
Тогда cos( δi – δ j – yij) = cos(φi – φj – 90° + αij), а с учетом четности функции косинус cos( δi – δj – 90°+ αij) = cos(90° – δi + δj – αij). Имея в виду, что cos(90° – δ) = sin( δ), получим cos(90° – δi + δj – αij) = sin( δi – δj + αij).
Аналогично sin( δi – δj – yij) = sin( δi – δj – 90 + αij) = –sin(90° – δi + + δj – αij), получим –sin(90° – δb), в силу нечетности функции синус. Так как sin(90° – δ) = cos( δi + δj – αij) = –cos( δi – δj + αij). Подставляя полученные соотношения в (3.51), будем иметь:
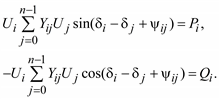(3.52)
В полученной системе нелинейных уравнений установившегося режима искомыми переменными являются модули и фазовые углы напряжений, в то время как в уравнениях (3.46) неизвестными являются вещественная и мнимая составляющие напряжений.
Дата: 2019-07-30, просмотров: 420.
