Генераторными узлами называют узлы, в которых генерируется активная мощность. Реактивная мощность, как правило, также генерируется в узлах. Генераторные узлы – это шины электрических станций или шины мощной системы, схема которой не входит в модель для расчетной схемы. Моделируются генераторные узлы по-разному:
· так же, как и узел нагрузки, – постоянными значениями активной и реактивной мощности, но с противоположным знаком;
· постоянным значением активной мощности и фиксированным значением модуля напряжения в узле. Реактивная мощность не известна и подлежит расчету;
· генераторный узел – это базисный и балансирующий узел одновременно. Активная и реактивная мощности узла подлежат вычислению;
· генераторный узел – это базисный узел, но с известными значениями активной и реактивной мощности – заданы все четыре независимых параметра режима – P, Q, U, φ;
· генераторный узел – это балансирующий узел, но напряжение в нем не известно ни по модулю, ни по фазе. Подлежат определению все четыре независимых параметра режима – P, Q, U, φ.
При фиксации активной мощности и модуля напряжения обычно в уравнения установившегося режима входит уравнение для активной мощности узла (3.46) и уравнение вида: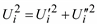 
, где Ui задано, а 
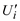и 
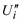подлежат определению.
В тех случаях, когда для одного из узлов требуется задать все четыре независимых параметра режима – P, Q, U, φ (базисный узел), то в сети должен появиться узел, в котором не известен ни один из этих четырех параметров – балансирующий узел. Происходит разделение балансирующего и базисного узлов.
Форма уравнений установившегося режима меняется, а именно –перестраивается матрица узловых проводимостей. Так, например, если для графа сети на рис. 3.10 базисным стал узел 2, а балансирующим остался узел 0, то матрица Y принимает вид:
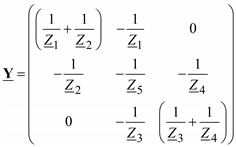
Математические модели линии
В простейшем представлении линия электропередачи – это проводники, протянутые на большое расстояние, по которым передается электрическая энергия. Возможность передачи электроэнергии обусловлена главным образом большим напряжением, при котором потери при передаче снижаются до приемлемого уровня.
Конструктивно воздушные ЛЭП представляет собой провода, подвешенные на безопасном расстоянии от земли, или кабели, в которых проводящие жилы изолированы друг от друга и от внешней среды и защищены различными покровами и броней. В зависимости от конструкции ЛЭП называют воздушными (ВЛ) или кабельными линиями (КЛ).
Практически во всем мире для передачи электрической энергии принята система трехфазного переменного тока 50 или 60 Гц. Однако в некоторых случаях применяются другие системы переменного тока и передачи постоянного тока. Будем рассматривать только трехфазные воздушные линии переменного тока высокого напряжения (до 1150 кВ), передающие электроэнергию на большие расстояния (до нескольких тысяч километров).
Передача электроэнергии по ЛЭП переменного тока обусловлена распространением электромагнитного поля в проводах и окружающем пространстве. Возникновение переменного электростатического поля приводит к появлению токов смещения – зарядных токов (рис. 2.1). Зарядные токи, накладываясь на нагрузочный ток, определяют постепенное изменение тока вдоль линии. Магнитное поле, обусловленное током линии, характеризуется напряженностью, также изменяющейся вдоль линии. Это приводит к наведению ЭДС самоиндукции и взаимоиндукции, неравных для различных участков линии. Неравенство этих ЭДС определяет сложный закон изменения напряжения вдоль линии, в свою очередь определяющий изменение токов смещения вдоль линии.
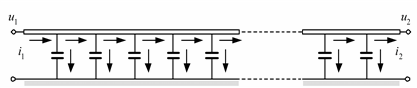
Рис. 2.1. Условное изображение распределения токов вдоль провода ЛЭП
В общем случае ЛЭП следует рассматривать как объект с распределенными вдоль одной пространственной координаты параметрами (вдоль линии). Параметры линии электропередачи, к которым относятся активное сопротивление, индуктивность, активная проводимость и емкость на единицу длины, считают равномерно распределенными вдоль ее длины. Такое свойство линий называют однородностью.
Провода ВЛ имеют в качестве проводящего материала алюминий или его сплав. Практически всегда используются сталеалюминиевые провода марки АС. Их удельное сопротивление постоянному току в среднем равно r = 29,1 Ом мм2 / км. Активное сопротивление переменному току больше сопротивления постоянному току вследствие поверхностного эффекта, однако для частоты 50 Гц это различие несущественно. Активное сопротивление в электрических схемах ЛЭП является параметром, определяющим процесс диссипации (рассеивания) энергии в виде отдачи тепла в окружающее пространство.
Индуктивность ЛЭП вызвана явлениями самоиндукции и взаимоиндукции фаз линии и определяется в зависимости от диаметра проводов фазы и расстояния между фазами. В практике расчетов электрических сетей используют индуктивное сопротивление фаз ЛЭП. Погонное индуктивное сопротивление ВЛ 330–1150 кВ x0 в среднем равно 0,31 Ом / км.
Вследствие несовершенства изоляции ВЛ и явления короны в местах присоединения проводов к гирляндам изоляторов ВЛ имеют место потери электроэнергии от токов утечки по изоляторам ВЛ и короны. Большое влияние на эти потери оказывают влажность и загрязнение окружающего воздуха. В зависимости от погоды потери от токов утечки и на корону могут изменяться в десятки раз.
Моделирование потерь в изоляции ВЛ можно выполнить с помощью введения активной проводимости g0, величина которой определяется по экспериментальным данным, полученным в результате наблюдений и расчетов существующих ВЛ. Для большинства ВЛ 330–1150 кВ погонная активная проводимость задается в пределах 0,01…0,1 мкСм / км.
Емкостные проводимости между фазами и между проводами и землей, грозозащитными тросами и заземленными частями опоры моделируются одним параметром – емкостной проводимостью фазы b0. Величина погонной емкостной проводимости ВЛ 330–1150 кВ в среднем составляет 3,5 мкСм / км.
В цепи с распределенными параметрами интервал времени распространения электромагнитных волн вдоль линии сопоставим с интервалом времени, в течение которого токи и напряжения изменяются на заметную величину от полного их изменения.
Другими свойствами линии электропередачи можно считать:
· непрерывность переменных;
· стационарность;
· одномерность в отношении пространства и многомерность в отношении переменных, характеризующих работы линии в разных точках линии;
· статизм или динамичность (в зависимости от исследуемых процессов);
· линейность или нелинейность (в зависимости от уравнений, описывающих режим работы линии) – при этом параметры линии считаются постоянными величинами.
В отношении детерминированности и стохастичности рассматриваются разные подходы к моделированию линии – параметры и переменные могут быть представлены также и случайными величинами.
Элементы ЭЭС являются, как правило, трехфазными устройствами переменного тока, и ЛЭП имеет три фазы, которые присоединяются к другим трехфазным элементам сети, например, повышающим и понижающим трансформаторам (рис. 2.2, а).
Здесь и далее будем рассматривать только симметричные трехфазные системы, которые вследствие симметрии можно графически изображать в однолинейном виде (рис. 2.2, б), имея в виду, что протекающий по фазе переменный ток замыкается через две другие фазы. Кроме того, трехфазная система имеет нейтраль N, которая технически может отсутствовать, но токи утечки и емкостные токи в линии могут моделироваться посредством введения нейтральной точки (линии, плоскости). На рис. 2.2 соединение обмоток трансформаторов в звезду дает нейтральные точки трехфазной системы, которые могут иметь соединение с землей (заземление).
Выделим в линии на расстоянии x от начала линии (рис. 2.2, а, точка 1) участок бесконечно малой длины dx. На этом участке линии электрические параметры можно считать сосредоточенными (рис. 2.3).
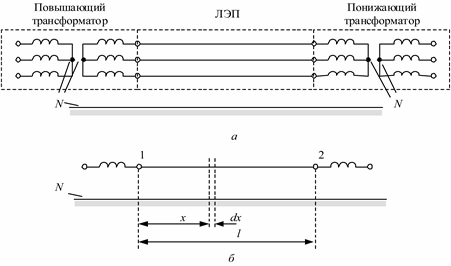
Рис. 2.2. Трехфазная линия электропередачи (а) и ее однолинейное изображение (б)
Составим уравнения Кирхгофа для электрической цепи на выделенном участке линии:
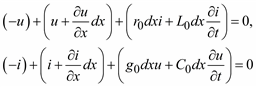21
или
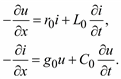22
Здесь в C0 и L0 учтены влияния соседних фаз линии.
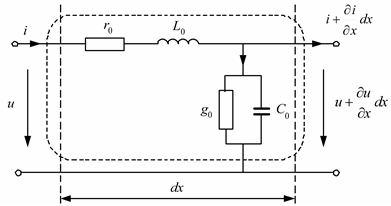
Рис. 2.3. Элементарный отрезок линии
Полученные уравнения являются дифференциальными уравнениями в частных производных – моделью участка линии на микроуровне. Независимые переменные в них – это время t и одна пространственная координата x.
Используя символический метод представления синусоидальных функций времени комплексными величинами, для действующих значений токов и напряжений можно записать:
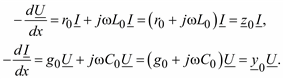23
Полученная система уравнений уже имеет одну независимую переменную x. Обозначим напряжения и токи по концам линии: U1 и I1 при x = 0 и U2 и I2 при x = l. Тогда из решения системы дифференциальных уравнений (2.3) получим связь между напряжениями и токами по концам линии:
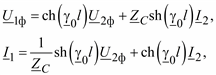24
где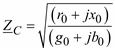 
– волновое сопротивление линии;
– коэффициент распространения волны;
α0 – коэффициент затухания волны;
β0 – коэффициент фазы.
Полученные уравнения называются уравнениями длинной линии или телеграфными уравнениями.
В (2.4) напряжения записаны в фазных значениях. Однако в трехфазных системах принято указывать линейные значения напряжений, что приводит к пересчету на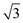 
некоторых слагаемых:
25
Чтобы не вводить в запись уравнений константу 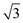и в то же время использовать линейные значения напряжений, используют увеличенное в 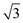значение тока линии. Таким образом, математическая модель длинной линии имеет вид
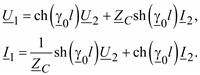26
Здесь I1 и I2 – фазные токи линии, увеличенные в .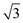
Когда необходимо вычислить напряжение и ток в какой-либо другой точке линии, находящейся на расстоянии x от начала линии (рис. 2.4), по напряжению и току в конце, используют модель:
27
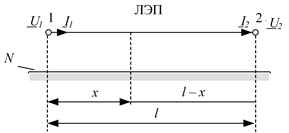
Рис. 2.4. Определение напряжения и тока в точке на линии
Формально напряжение и ток в любой точке линии можно рассматривать как результат наложения двух волн, движущихся в противоположные стороны. С течением времени волна напряжения перемещается от начала линии к ее концу; она носит название прямой или падающей волны. Волна напряжения, которая перемещается от конца линии к ее началу, носит название обратной или отраженной волны.
Расчеты показывают, что для воздушных линий электропередачи при частоте f = 50 Гц коэффициент фазы β0 ≈ 0,001 рад/км (0,06 град/км). С помощью этого значения можно найти длину прямой и обратной волн.
Введем понятие длины волны напряжения и тока λ, равной расстоянию между двумя точками линии, в которых фазы напряжения (тока) падающей или отраженной волны напряжения (тока) различаются на 2π.
28
где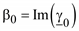 
– коэффициент фазы.
Скорость перемещения падающей волны вдоль линии называется фазовой скоростью волны. Это скорость перемещения точки, фаза колебания в которой остается постоянной:
29
Из этого соотношения с учетом ω = 2πf получим более точное значение коэффициента фазы
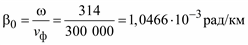210
и длины волны
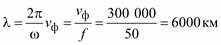. 211
Линии с длиной l = λ = 6000 км называют волновыми, а с l = λ / 2 = = 3000 км – полуволновыми линиями.
Для упрощения исследований режимов работы ЛЭП сверхвысокого напряжения иногда пользуются уравнениями идеальной линии, в которой активные параметры считаются равными нулю: r0 = 0, g0 = 0. Очевидно, что при этом α0 = 0.
С учетом
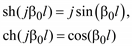212
получим математическую модель идеальной линии:
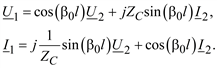213
Систему уравнений (2.6) можно представить как уравнения четырехполюсника (рис. 2.5).
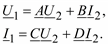214
Рис. 2.5. Четырехполюсник
Здесь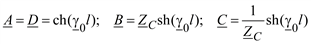 
, что позволяет считать данный четырехполюсник симметричным.
В практике расчетов удобно пользоваться П-образной схемой замещения линии (рис. 2.6).
Рис. 2.6. П-образная схема замещения ЛЭП
Найдем соотношения, связывающие параметры П-образной схемы замещения Z, Y1 и Y2 с параметрами модели длинной линии (2.6).
Запишем выражение, связывающее напряжения в начале U1 и конце U2 П-образной схемы замещения:
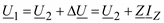, 215
где ΔU – падение напряжения в продольной ветви на параметре Z схемы замещения;
IZ – ток в ветви с параметром Z.
Соотношения между токами в ветвях схемы замещения получаются из первого закона Кирхгофа:
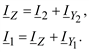216
Токи в поперечных ветвях с Y1 и Y2 вычисляются по формулам:
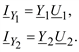217
Подставим ток IZ из (2.16) в (2.15) и с учетом (2.17) будем иметь:
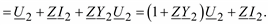218
Теперь запишем соотношение для тока в начале схемы замещения I1, выразив его также через напряжение и ток конца схемы замещения. Подставив в выражение для тока I1 из (2.16) выражения для тока IZ и тока IY1, получим
219
Подставим в это выражение U1 из (2.18), будем иметь:
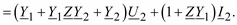220
Окончательно получаем систему уравнений для П-образной схемы замещения:
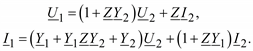221
Модель (2.21) по своей структуре совпадает с уравнениями четырехполюсника (2.14). Из этого с учетом вида модели длинной линии (2.6) следует, что
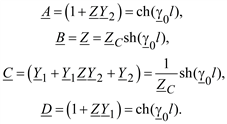222
Решение (2.22) относительно параметров П-образной схемы замещения дает:
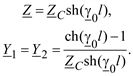223
Используя известные математические соотношения
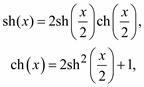224
получаем
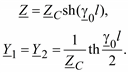225
Для идеальной линии параметры П-образной схемы замещения получаются в виде
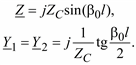226
Для П-образной схемы замещения ЛЭП (см. рис. 2.6) в п. 2.1.3 было получено
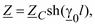
227
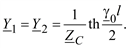
Величины составляющих комплексного параметра γ0 = α0 + jβ0 для линий сверхвысокого напряжения имеют порядок: α0 – 10–5 и β0 – 10–3. Поэтому когда длина линии l невелика, приближенно можно принять
228
Для параметров П-образной схемы замещения с математической моделью длинной линии получаем:
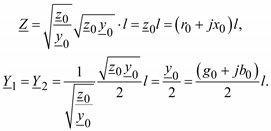229
Подставим в уравнения для П-образной схемы замещения (2.21) полученные значения (2.29):
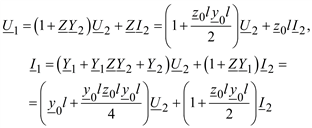230
или окончательно
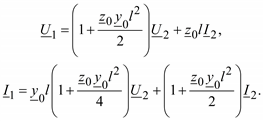231
Полученные уравнения являются упрощенной математической моделью ЛЭП, в которой не учитывается распределенность параметров, а сосредоточенные сопротивления и проводимости вычисляются по (2.29).
Для совсем коротких линий второе слагаемое в выражении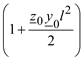 
является очень маленьким вследствие того, что проводимость 
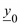имеет порядок 10–6 … 10–4. Тогда уравнения (2.31) приобретают еще более простой вид:
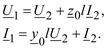232
Такая модель соответствует Г-образной схеме замещения линии, в которой только одна поперечная ветвь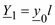 
.
Все математические модели ЛЭП удобно сопоставлять в табличной форме записи параметров четырехполюсника (табл. 2.3). Распределенность параметров в двух последних моделях не учитывается.
В других случаях пренебрегают либо сопротивлениями токоведущих жил линии (активным или реактивным), либо емкостной проводимостью между фазами линии.
Таблица 2.3
Коэффициенты четырехполюсника моделей ЛЭП
| Модель | A | B | C | D |
| Уравнения длинной линии |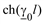 
| 
| 
|
|
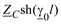
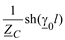
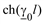
| Уравнения идеальной линии |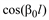 
| 
| 
|
|
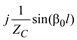
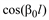
| Модель с сосредоточенными параметрами П-образной схемы замещения | 
| 
| 
|
|
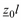
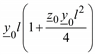
| Модель с сосредоточенными параметрами Г-образной схемы замещения | 1 |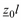
| 
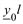
| 1 |
Модель трансформатора
Трансформатором называют статическое электромагнитное устройство, имеющее две (или более) индуктивно связанные обмотки и предназначенное для преобразования посредством электромагнитной индукции одной системы переменного тока в другую систему переменного тока. При этом число фаз, форма кривой напряжения (тока) и частота остаются неизменными.
Силовые трансформаторы применяются в системах передачи и распределения электроэнергии; для установок с преобразователями переменного тока в постоянный (выпрямители) или постоянного в переменный (инверторы); для получения требуемых напряжений питания у электроприемников. Силовые трансформаторы устанавливаются на электростанциях, на понижающих подстанциях, в центрах питания потребителей и непосредственно у потребителей электрической энергии.
В электрических сетях используются трехфазные трансформаторы или группы из трех однофазных трансформаторов. Силовые трансформаторы выполняют двухобмоточными и трехобмоточными. Существуют также трехобмоточные автотрансформаторы и двухобмоточные трансформаторы с расщепленной вторичной обмоткой.
Основными элементами силовых трансформаторов являются: магнитопровод, обмотки, изоляция, бак, расширитель и высоковольтные вводы. Другие части – это элементы системы охлаждения, устройства регулирования напряжения, а также защитные и измерительные устройства.
Магнитопровод является магнитной системой силового трансформатора и служит конструктивным основанием для установки и крепления обмоток, отводов от обмоток и других деталей (рис. 2.7). Магнитопровод выполняется из электротехнической стали.
Обмотки являются частью электрической цепи и состоят из обмоточного провода (медного или алюминиевого) и изоляционных деталей. К обмоткам также относят вводные концы обмоток, ответвления для регулирования напряжения и регулировочную обмотку, емкостные кольца и электростатические экраны емкостной защиты от перенапряжений.
Обмотки состоят из последовательно соединенных катушек, которые могут наматываться непрерывно, т. е. без паек. Между катушками ставятся прокладки из электрокартона. Фазы обмоток одного напряжения соединяются между собой в звезду или треугольник.
Рис. 2.7. Магнитопровод с обмотками силового трансформатора
В трансформаторах с масляным охлаждением магнитопровод с обмотками помещают в бак с трансформаторным маслом (рис. 2.8). Омывая обмотки и магнитопровод, трансформаторное масло отбирает от них тепло и, обладая большей теплопроводностью, чем воздух, через стенки радиатора отдает ее в окружающую среду.
Существуют также сухие трансформаторы.
Вводы предназначены для присоединения к сборным шинам распределительных устройств станций и подстанций. Ввод состоит из токопроводящей части, металлического фланца, служащего для крепления на крышке бака, и фарфорового изолятора.
Для компенсации температурных изменений применяется расширитель, помещенный в верхней части бака трансформатора или отдельным выносным баком.
Принцип действия трансформатора основан на явлении электромагнитной индукции. При подключении первичной обмотки к источнику переменного тока c напряжением u1 в витках этой обмотки протекает переменный ток i1, который создает в магнитопроводе переменный магнитный поток Ф. Замыкаясь на магнитопроводе, этот поток сцепляется с обеими обмотками (первичной и вторичной) и индуктирует в них ЭДС:
233
где w1 и w2 – число витков в первичной и вторичной обмотках трансформатора.
При подключении нагрузки к выводам вторичной обмотки трансформатора под действием ЭДС е2 в цепи этой обмотки создается ток i2, а на выводах вторичной обмотки устанавливается напряжение u2.
Из (2.33) следует, что ЭДС е1 и е2 отличаются друг от друга числом витков обмоток, в которых они наводятся. Поэтому, применяя обмотки с требуемым соотношением витков, можно изготовить трансформатор на любое отношение напряжений.
Обмотку трансформатора, подключенную к сети с более высоким напряжением, называют обмоткой высшего напряжения (ВН); обмотку, присоединенную к сети меньшего напряжения, – обмоткой низшего напряжения (НH).
Трансформаторы обладают свойством обратимости; один и тот же трансформатор можно использовать в качестве повышающего и понижающего. Но обычно трансформатор имеет определенное назначение: либо он является повышающим, либо понижающим.
Трансформатор – это аппарат переменного тока. Если же его первичную обмотку подключить к источнику постоянного тока, то магнитный поток и магнитопроводе трансформатора также будет постоянным как по величине, так и по направлению (dΦ/dt = 0). Поэтому и в обмотках трансформатора не будет наводиться ЭДС.
Основными электрическими элементами силового трансформатора являются обмотки, имеющие электрическое сопротивление. Ток, протекая по этим обмоткам, вызывает их нагрев. Потоки рассеивания обмоток обусловливают собственные индуктивности обмоток. Следовательно, в обмотках трансформатора, по которым протекают токи, имеются активные и индуктивные сопротивления.
Процесс намагничивания активной стали магнитопровода характеризуется кривой намагничивания B = f(H). Эта зависимость является нелинейной: на кривой имеется участок, после которого дальнейший рост напряженности магнитного поля практически не приводит к увеличению индукции в стали. Эта зона характеризует насыщение электротехнической стали. Отношение индукции к напряженности поля в любой точке кривой намагничивания называют магнитной проницаемостью (µ), которая характеризует способность материала к намагничиванию. Зависимость магнитной проницаемости электротехнической стали от индукции является также нелинейной.
Вследствие непрерывного изменения величины и направления намагничивающего тока, протекающего в первичной обмотке трансформатора, в магнитопроводе создается переменный магнитный поток, изменение которого приводит к перемагничиванию электротехнической стали.
Электрическая энергия, затраченная на перемагничивание, преобразуется в тепловую энергию, приводящую к нагреву магнитопровода трансформатора.
Потери в активной части магнитопровода обусловливаются природой процессов намагничивания ферромагнитных материалов и состоят из трех частей: потерь на гистерезис (Рг), потерь на вихревые токи (Рв) и потерь на магнитное последействие (Pп)
Потери на гистерезис при перемагничивании вызываются затратой энергии на перестройку границ доменов, и направления их самопроизвольной намагниченности в электротехнической стали зависят от ее микроструктуры и параметров внешнего магнитного поля.
Потери на вихревые токи вызываются затратой энергии на нагрев активной стали от вихревых токов, наводимых в ней переменным магнитным потоком. Вихревые токи циркулируют в листах в плоскостях, перпендикулярных направлению магнитного потока, т. е. в плоскостях поперечного сечения магнитопровода.
Величина потерь на вихревые токи пропорциональна квадрату толщины и обратно пропорциональна удельному электрическому сопротивлению активного материала, поэтому для уменьшения потерь на вихревые токи магнитопровод набирается из тонких, изолированных друг от друга слоев, толщина которых в основном определяется толщиной электротехнической стали. Слои магнитопровода выполняются из отдельных пластин или лент.
Измеренные потери в стали всегда больше, чем расчетная сумма потерь на гистерезис и на вихревые токи, за счет наличия потерь на магнитное последействие или, как их иногда называют, «дополнительных» потерь. Природа этих потерь в настоящее время недостаточно ясна, и они не поддаются аналитическому расчету. Увеличение общих потерь в стали магнитопровода может быть вызвано также за счет механических воздействий на нее при технологической обработке и несовершенства межлистовой изоляции. Кроме того, потоки рассеивания обмоток частично замыкаются через бак и другие стальные элементы трансформатора, что вызывает дополнительные потери на перемагничивание и вихревые токи. Для снижения этих потерь стальные баки трансформатора экранируют пакетами электротехнической стали или пластинами из немагнитных материалов (меди, алюминия).
Ток намагничивания и ток, вызывающий потери в стали трансформатора, также протекает по первичной обмотке. Вследствие нелинейности характеристики намагничивания ток намагничивания не является синусоидальным – зависимость тока намагничивания от времени является периодической функцией, но с несколько вытянутой по отношению к функции синуса формой кривой. Так как нагрузочный ток обычно в десятки раз больше тока намагничивания, то суммарный ток (намагничивания и нагрузочный) первичной обмотки является практически синусоидальным. В режимах работы трансформатора, близких к холостому ходу, следует считаться с несинусоидальностью тока трансформатора. Несинусоидальность тока трансформатора сильно увеличивается при возрастании тока намагничивания, что происходит при превышении напряжения, поданного на трансформатор.
Модель
Рассмотрим математические модели силовых трансформаторов, которые применяются в задачах, связанных с расчетом установившихся режимов схем электрических сетей. В таких моделях не учитываются емкостные связи между витками каждой из обмоток, между самими обмотками и обмотками и землей, а также распределенность электрических и магнитных параметров. Кроме того, ограничимся рассмотрением симметричных режимов нагрузки трансформаторов.
Получим математическую модель однофазного двухобмоточного трансформатора. Вначале предположим, что трансформатор не имеет магнитопровода (воздушный трансформатор), тогда он может быть представлен схемой рис. 2.9, в которой активные сопротивления обмоток изображены отдельно. Полярности обмоток на схеме отмечены звездочками.
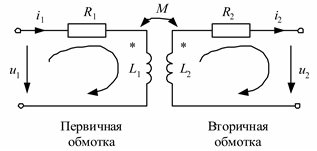
Рис. 2.9. Схема трансформатора без магнитопровода
При обходе контуров на схеме рис. 2.9 в соответствии с заданными направлениями по второму закону Кирхгофа получим уравнения трансформатора в дифференциальной форме:
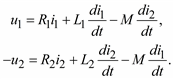234
Так как направления токов на схеме ориентированы не одинаково по отношению к звездочкам, то полярность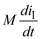 
не совпадает с i2 и, наоборот, полярность 
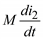не совпадает с i1.
При синусоидальных токах и напряжениях уравнения (2.34) в комплексной форме записываются следующим образом:
235
Эти уравнения равносильны следующим:
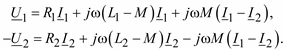236
Последним уравнениям соответствует схема замещения рис. 2.10. В отличие от рис. 2.9 в схеме замещения первичная и вторичная цепи трансформатора связаны не индуктивно, а гальванически.
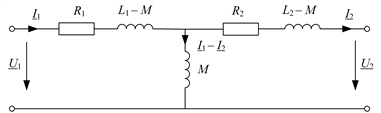
Рис. 2.10. Схема замещения трансформатора без магнитопровода
Входящие в схему рис. 2.10 разности L1 – M и L2 – M имеют физический смысл только при одинаковом числе витков первичной w1 и вторичной w2 обмоток (w1 = w2). В этом случае они представляют собой индуктивности рассеяния Ls1 и Ls2 первичной и вторичной обмоток трансформатора.
В реальных трансформаторах для моделирования потерь в стали в схему замещения трансформатора вводят активную проводимость Gμ. Для моделирования эффекта намагничивания сердечника вводят реактивную проводимость Bμ.
Если взять за основу математической модели трансформатора так называемый идеальный трансформатор с коэффициентом трансформации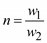 
, для которого относительная магнитная проницаемость равна бесконечности и ток намагничивания равен нулю, то добавлением к нему элементов, учитывающих основные паразитные эффекты, можно получить полную схему замещения трансформатора (рис 2.11).
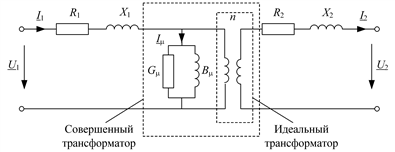
Рис. 2.11. Полная Т-образная схема замещения трансформатора
Потери энергии в обмотках трансформатора при протекании по ним токов учитываются активными сопротивлениями R1 и R2, последовательно с ними включены индуктивности рассеяния, которые учитывают эффект запасания энергии и наведения напряжения в обмотках от потоков рассеяния. Этим индуктивностям соответствуют индуктивные сопротивления обмоток X1 и X2. Ток намагничивания обусловливает намагничивающую силу, которая создает поток взаимной индукции. Величина тока намагничивания Iµпропорциональна напряжению первичной обмотки. Параллельно индуктивной проводимости намагничивания Bµвключают активную проводимость Gµ, учитывающую потери в сердечнике.
Таким образом, идеальным трансформатором является трансформатор, для которого при любых условиях 
.
Трансформатор, для которого при любой нагрузке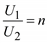 
, называется совершенным трансформатором (рис. 2.11).
Во многих случаях пользуются приведенной Т-образной схемой замещения трансформатора (рис 2.12). Получается она приведениям сопротивлений вторичной обмотки к напряжению первичной обмотки по соотношениям:
Рис. 2.12. Приведенная Т-образная схема замещения трансформатора
На схеме рис. 2.12 отмечены ток и напряжение:
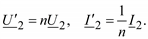237
Обычно для силовых трансформаторов более целесообразна так называемая Г-образная схема замещения, элементы которой имеют простой физический смысл и могут быть вычислены или измерены. Получается она следующим образом.
Ветвь намагничивания переносится на зажимы первичной обмотки и оказывается включенной на напряжение U1. Это вносит погрешность в математическую модель, так как в действительности ток намагничивания (ток холостого хода) протекает по первичной обмотке. Обычно ток холостого хода силовых трансформаторов меньше одного процента от номинального тока трансформатора, и такое упрощение считается допустимым. Сопротивления первичной обмотки оказываются последовательно включенными с приведенными сопротивлениями вторичной обмотки, и при их сложении получаются так называемые сопротивления трансформатора Rт и Xт (рис. 2.13):
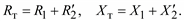
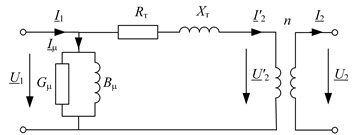
Рис. 2.13. Г-образная схема замещения трансформатора
Полученная схема носит название Г-образной схемы замещения трансформатора и применяется для выполнения расчетов схем электрических сетей, где она еще больше упрощается посредством представления ветви холостого хода в виде постоянных величин потерь активной и реактивной мощности на холостой ход (рис 2.14).
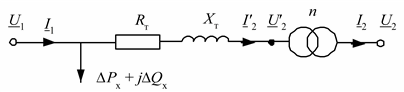
Рис. 2.14. Упрощенная Г-образная схема замещения трансформатора
Все полученное выше для однофазных трансформаторов можно распространить на каждую фазу трехфазного трансформатора.
Сопротивления и проводимости Г-образной схемы замещения трансформатора, приведенные к напряжению обмотки первичного напряжения, определяются по формулам:
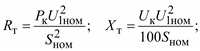
238
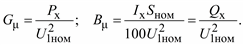
Моделирование элементов схем электрических сетей при использовании специальных программ для расчета их режимов работы удобно выполнять по П-образным схемам замещения. Такую схему замещения можно получить и для трансформатора.
Получим параметры П-образной схемы замещения (см. рис. 2.6) на основе Г-образной схемы замещения двухобмоточного понижающего трансформатора с коэффициентом трансформации n > 1 (рис. 2.13).
Найдем напряжение и ток первичной обмотки:
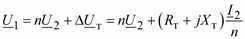, 239
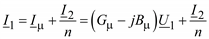. 240
После подстановки (2.39) в (2.40) получим
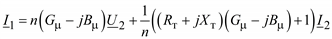. 241
Сопоставляя выражения (2.39) и (2.41) с уравнениями четырехполюсника
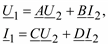242
и учитывая соотношения между коэффициентами четырехполюсника и параметрами П-образной схемы замещения [см. (2.22)]:
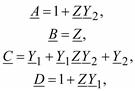243
будем иметь:
244
Из полученных соотношений можно найти параметры П-образной схемы замещения трансформатора:
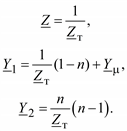245
П-образная схема замещения трансформатора в отличие от П-об-разной схемы замещения ЛЭП является несимметричной, т. е. Y1 ≠ Y2.
Внешней характеристикой трансформатора называют зависимость изменения вторичного напряжения U2 от тока нагрузки I2 при постоянном коэффициенте мощности приемника cos φ = const и номинальном первичном напряжении U1 = Uном. Сопоставляя внешние характеристики, полученные для различных математических моделей трансформатора, с экспериментально найденной характеристикой трансформатора, можно оценить величину погрешности различных моделей и определить, таким образом, область их использования.
Построим внешнюю характеристику силового трансформатора по его математической модели при изменении тока вторичной обмотки от нуля до Iном для трех различных коэффициентов мощности: 0,8; 0,9 и 1,0.
Внешнюю характеристику U2 = f(I2) построим по уравнению
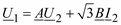. 246
Примем U1 = U1 = const (совместим с вещественной осью), тогда векторная диаграмма токов и напряжений трансформатора будет иметь вид, как на рис. 2.15.
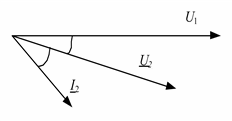
Рис. 2.15. Векторная диаграмма токов и напряжений 1
Выразим из (2.46) напряжение U2:
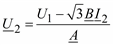. 247
Здесь ток I2 имеет угол сдвига относительно вещественной оси –(δ + φ), а напряжение вторичной обмотки представлено в комплексном виде: |U2| и δ, где δ входит в левую часть уравнения: U2 = U2e–jδ и в правую: I2 = I2e–j(φ + δ).
Чтобы получить зависимость величины (модуля) U2 от величины (модуля) I2, необходимо перейти к уравнениям с вещественными переменными. Для удобства примем совмещенным с действительной осью вектор U2, тогда векторная диаграмма токов и напряжений примет вид, показанный на рис. 2.16.
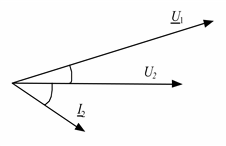
Рис. 2.16. Векторная диаграмма токов и напряжений 2
Тогда напряжение U2:
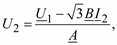248
где U1 = U1ejδ; I2 = I2e–jφ.
Разделим уравнение (2.48) на два уравнения с вещественными переменными. С учетом A = A = n и B = B' + jB'' будем иметь систему уравнений:
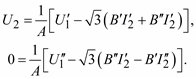249
Так как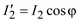 
, 
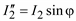и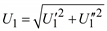 
, то получаем систему уравнений
250
с неизвестными U2, U1′ и U1′′.
Изменяя ток I2 в пределах от нуля до I2ном, будем искать решение системы уравнений (2.50) для каждого значения I2 и строить зависимость U2 = f(I2).
В Mathcad имеется возможность определения функции как решения системы уравнений. Для этого выражение с Find имеет вид определения функции: f(x) := Find(x) и далее в документе Mathcad f(x) становится определенной и является функцией аргумента x.
В нашем случае аргументами функции с Find будет U2 (по условию с углом равным нулю) и cos φ, который также будет различным для разных выходных характеристик.
Пример 1. Определим функцию как решение системы уравнений.
Для удобства записи введем еще две переменные I'2 = I2 cos φ и I''2 = I2 sin φ.
Начальные приближения:
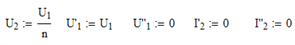
Решающий блок Mathcad:
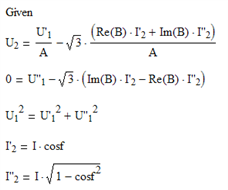
Функция как решение системы уравнений:
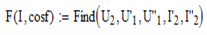
Здесь функция F является вектор-функцией, т. е. содержит пять элементов (по числу неизвестных). Первый элемент дает функцию U2, второй – U′1 и т. д. Нас интересует только первый элемент: функция U2 от I2 и cos φ. Если переменная ORIGIN в Mathcad имеет заданное по умолчанию значение 0, то наша функция будет использоваться в виде F(I2, cosφ)0. Так, например, для cos φ = 0,8 выходная характеристика будет строиться по функции F(I2, 0.8)0 при изменении тока от 0 до Iном.
Моделирование нагрузок
Процесс потребления электрической энергии отождествляется с понятием электрической нагрузки, которая характеризуется мощностью и энергией. Нагрузкой может быть один электроприемник, группа однотипных электроприемников или совокупность различных электроприемников – смешанная нагрузка.
К основным электроприемникам в электрической системе относятся:
· асинхронные двигатели,
· синхронные двигатели,
· лампы накаливания,
· люминесцентные лампы,
· печи сопротивления,
· дуговые печи.
Существует также большое число устройств и бытовых приборов, в которых сочетаются различные по типу электроприемники.
В задачах анализа установившихся режимов электрических систем необходима величина активной и реактивной мощности нагрузки. Физическая природа потребления энергии электрической нагрузкой такова, что ее активная и реактивная мощности зависят от подведенного напряжения и частоты в электрической системе. Такие зависимости носят название статических характеристик нагрузок по частоте и по напряжению. Разные типы электрических нагрузок имеют различные статические характеристики. В совокупности различных типов электроприемников рассматриваются статические характеристики смешанной нагрузки.
Статические характеристики используются при регулировании частоты и напряжения в ЭЭС. В общем они записываются как 
.
Здесь мы будем рассматривать зависимости мощности нагрузки только от напряжения – статические характеристики нагрузки по напряжению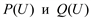 
. При этом будем считать частоту в ЭЭС неизменной величиной. По статическим характеристикам, построенным в относительных номинальных единицах, могут быть определены регулирующие эффекты нагрузки – как производные 
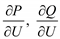в какой-либо рабочей точке характеристики, например при U = Uном.
Регулирующий эффект показывает степень снижения активной и реактивной нагрузки при изменении напряжения. Чем больше регулирующий эффект, тем сильнее изменяется мощность, потребляемая нагрузкой при изменении напряжения или частоты.
Для различных электроприемников и их сочетаний статические характеристики получаются разными и зависящими от их рабочих режимов. Практически приходится пользоваться статическими характеристиками, полученными экспериментально. В некоторых случаях их удается получить расчетным путем.
Статические характеристики изображают в координатах относительных величин – активной и реактивной мощности от частоты и напряжения (рис. 2.17).
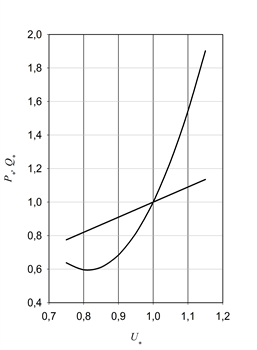
Рис. 2.17. Средние статические нагрузки по напряжению для смешанной нагрузки
На рис. 2.17 относительная величина напряжения U* = U / Uном, а относительные мощности определяются по отношению к номинальной или какой либо выбранной величине мощности нагрузки: P* = P / Pном, Q* = Q / Qном.
Следует отметить, что в ЭЭС и конкретно у потребителей устанавливаются специальные автоматические регулирующие устройства, которые компенсируют изменение напряжения на электроприемниках, что в значительной мере снижает регулирующие эффекты нагрузки. В простейшем случае это стабилизаторы напряжения, а в высоковольтных сетях – мощные регулируемые компенсирующие устройства реактивной мощности и регуляторы напряжения силовых трансформаторов. Рассмотрим статические характеристики отдельных видов нагрузки.
Асинхронные двигатели
Принцип действия асинхронного двигателя основан на явлении электромагнитной индукции. В неподвижную трехфазную обмотку статора асинхронного двигателя подается переменный ток, который формирует в статоре вращающееся магнитное поле. Это поле пересекает проводники замкнутой обмотки ротора и наводит в них ЭДС, под действием которых по обмотке ротора будет протекать ток. Взаимодействие этого тока с полем статора создает на проводниках обмотки ротора электромагнитные силы – вращающий момент, направление которого определяется по правилу «левой руки». Эти силы увлекают ротор в сторону вращения магнитного потока. Скорость вращения ротора всегда меньше скорости вращения магнитного поля статора. Если предположить, что в какой-то момент времени частота вращения ротора оказалась равной частоте вращения поля статора, то проводники обмотки ротора не будут пересекать магнитное поле статора и тока в роторе не будет. В этом случае вращающий момент станет равным нулю, и частота вращения ротора уменьшится по сравнению с частотой вращения поля статора, пока не возникнет вращающий момент, уравновешивающий момент нагрузки на валу двигателя и момент сил трения в подшипниках.
Асинхронные двигатели имеют различные статические характеристики. Активная мощность двигателей в значительной мере зависит от характеристик машин, приводимых во вращение двигателями. Реактивная мощность имеет разную зависимость от напряжения, обусловленную номинальной мощностью двигателя. Маломощные двигатели имеют более крутые характеристики по сравнению с мощными двигателями.
Реактивная мощность, потребляемая асинхронными двигателями, складывается из намагничивающей мощности, связанной с намагничивающим током, и мощности рассеяния, связанной с созданием полей рассеяния в статоре и роторе. При снижении напряжения реактивная мощность рассеяния растет, а намагничивающая мощность снижается. Суммарная мощность вначале снижается, а затем вновь начинает расти. При определенном напряжении, называемом критическим, дви-гатель останавливается и его дальнейшая работа становиться невозможной.
Синхронные двигатели
Вращающееся магнитное поле статора синхронной машины увлекает за собой ротор, который является электромагнитом-индуктором. Разноименные полюса магнитного поля статора и ротора притягиваются, и ротор вращается с постоянной скоростью. Для того чтобы ротор стал электромагнитом, на него подается постоянный ток – ток возбуждения. Этот ток при вращении ротора вызывает магнитное поле в статоре – реакцию якоря. В зависимости от величины тока возбуждения синхронный двигатель может работать в режиме перевозбуждения или недовозбуждения. Режим перевозбуждения – это нормальный режим работы двигателя. Мощные синхронные двигатели изготавливают с номинальным коэффициентом мощности 0,9 и 0,8 при работе с перевозбуждением.
В режиме перевозбуждения синхронный двигатель выдает реактивную мощность, т. е. имеет емкостный характер реактивной мощности по отношению к сети. При недовозбуждении синхронный двигатель имеет реактивную мощность индуктивного характера, но вследствие ограничений по устойчивости работы и перегреву лобовых частей машины максимально возможная потребляемая реактивная мощность не превышает 30 % от номинальной реактивной мощности при перевозбуждении.
Синхронные двигатели используются как источники реактивной мощности в ЭЭС и применяются для регулирования напряжения. Ток возбуждения синхронных машин изменяется в соответствии с законом регулирования напряжения в сети, поэтому статические характеристики синхронного двигателя по реактивной мощности зависят от закона регулирования напряжения в узле нагрузки, к которому он присоединен. В целом синхронные двигатели имеют положительный регулирующий эффект как по активной, так и по реактивной мощности.
Осветительная нагрузка
Установки электрического освещения с лампами накаливания, люминесцентными, дуговыми ртутными, натриевыми, ксеноновыми применяются на всех предприятиях для внутреннего и наружного освещения, для бытовых потребителей, нужд городского освещения и т. д.
Лампы накаливания излучают свет за счет свечения нити накаливания при большой температуре. При этом значительная часть потребляемой лампами накаливания энергии тратится на превращение в тепловую энергию. Если считать сопротивление R нити накаливания неизменным, а индуктивным сопротивлением пренебречь, то активная мощность лампы будет пропорциональна квадрату подведенного напряжения:
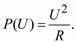251
Однако с изменением тока, протекающего по нити накаливания, ее температура и сопротивление меняются: с увеличением тока растет температура и увеличивается сопротивление нити и, наоборот, при снижении напряжения нить остывает и сопротивление снижается.
Экспериментально установлено, что потребляемая лампами накаливания мощность пропорциональна напряжению в степени 1,5…1,6. Реактивная мощность лампами накаливания практически не потребляется.
Люминесцентные лампы менее чувствительны к отклонениям напряжения. При повышении напряжения потребляемая мощность и световой поток увеличиваются, а при снижении – уменьшаются, но не в такой степени, как у ламп накаливания. Однако при снижении напряжения на люминесцентных лампах до величины 0,9Uном они начинают мерцать, а при величине напряжения 0,8Uном просто не загораются. Регулирующий эффект люминесцентных ламп по схеме с расщепленной фазой равен примерно 1,9 для активной мощности, а для реактивной мощности может быть оценен величиной 1,5.
Печи сопротивления
Они имеют характеристики, схожие с характеристиками ламп накаливания.
Дуговые печи
Дуговые печи представляют собой сложную и тяжелую нагрузку для энергосети – это крупный несимметричный и в высокой степени нестабильный потребитель по реактивной мощности. Флуктуации реактивной мощности, особенно выраженные на стадии расплава, приводят к падениям напряжения, уменьшающим активную мощность, поступающую к электропечи и другим электрическим нагрузкам, подсоединенным к тем же шинам распределительного устройства. Активная мощность, потребляемая печью, меняется пропорционально квадрату напряжения.
Компенсирующие устройства
Устройства типа индуктивности и емкости имеют квадратичные зависимости реактивной мощности от напряжения (если их реактивные сопротивления постоянны). Емкостная нагрузка имеет отрицательный регулирующий эффект.
Большинство компенсирующих устройств в настоящее время выпускаются с регулирующими устройствами, т. е. при изменении напряжения на шинах, где подключены компенсирующие устройства, последние изменяют свою мощность в соответствии с законом регулирования. Чаще всего компенсирующие устройства стабилизируют напряжение, т. е. поддерживают его на заданном уровне, что эквивалентно положительному регулирующему эффекту.
Модели
Статические характеристики для каждого типа электрической нагрузки и их совокупностей могут быть получены экспериментально. Однако в каждом конкретном случае это затруднительно и чаще всего пользуются так называемыми типовыми характеристиками. Так, например, можно выделить статические характеристики асинхронных двигателей малой, средней и большой мощности или статические характеристики определенного состава смешанной нагрузки. Полученные по таким нагрузкам статические характеристики обобщаются и представляются в виде математических моделей. В общем случае статические характеристики нагрузки по напряжению могут быть представлены в виде
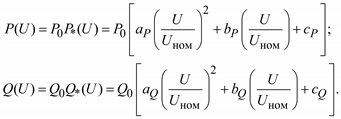252
где P0 и Q0 – активная и реактивная мощности нагрузки при номинальном напряжении; P*(U) и Q*(U) – статические характеристики нагрузок в относительных единицах; Uном – номинальное напряжение нагрузки или сети; aP, aQ, bP, bQ, cP и cQ – коэффициенты (параметры) моделей, полученные в результате обработки экспериментальных данных.
Средние статические характеристики примерно соответствуют следующему составу нагрузки, %:
Крупные асинхронные двигатели 15
Мелкие асинхронные двигатели 35
Крупные синхронные двигатели 9
Печи и ртутные выпрямители 11
Освещение и бытовая нагрузка 22
Потери в сетях 8
Обычно принимается aP = 0, т. е. линейная зависимость активной нагрузки от напряжения. Коэффициенты bP и cP в зависимости от характеристики узла нагрузки приведены в табл. 2.4.
Таблица 2.4
Значения коэффициентов bP и cP
| Характер нагрузки |
|
| Преобладают крупные промышленные предприятия | 0,3 | 0,7 | 0,6 | 0,4 | 0,9 | 0,1 |
| В среднем | 0,4 | 0,6 | 0,9 | 0,1 | 1,4 | –0,4 |
| Крупных промышленных предприятий нет | 0,9 | 0,1 | 1,2 | –0,2 | 1,5 | –0,5 |
Коэффициенты aQ, bQ и cQ в зависимости от коэффициента мощности приведены в табл. 2.5.
Таблица 2.5
Значения коэффициентов aQ, bQ и cQ
| Коэффициент мощности |
|
| 0,83…0,87 | 10 | –18 | 9 | 9,6 | –15,3 | 6,7 | 10 | –14,4 | 5,4 |
| 0,88…0,90 | 11,9 | –21,8 | 10,9 | 11,4 | –18,5 | 8,1 | 11,9 | –17,4 | 6,5 |
| 0,91…0,93 | 14,1 | –26,2 | 13,1 | 13,5 | –22,2 | 9,7 | 14,1 | –21 | 7,9 |
Моделирование электрических нагрузок статическими характеристиками по напряжению в расчетах установившихся режимов считается наиболее точным способом учета потребляемой мощности нагрузки. Однако для получения действительных статических характеристик требуются экспериментальные исследования, а для подбора типовых статических характеристик должен быть известен состав нагрузки, который может сильно изменяться во времени. Кроме того, в этом случае в расчетах непременно следует учитывать действие регуляторов напряжения, что значительно усложняет подготовку данных и требует знания законов регулирования.
Поэтому в большинстве случаев пользуются самой простой моделью нагрузки – постоянными значениями активной и реактивной мощности: P = const, Q = const.
В некоторых задачах, в которых выполняются расчеты установившихся режимов, токов короткого замыкания в электрической сети или расчеты устойчивости ЭЭС, нагрузки принято представлять схемами замещения. Такое представление является точным в том случае, если для нагрузки известны ее статические характеристики и величина подведенного напряжения. В других случаях такие модели являются приближенными.
Рассмотрим электрическую цепь, в которой имеется нагрузка, представленная в виде сопротивления Zн. Это сопротивление в общем случае является переменной величиной – получается нелинейная электрическая цепь. Даже если считать мощность, потребляемую нагрузкой, постоянной, сопротивление будет меняться в зависимости от напряжения по формуле
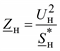. (2.53)
Кроме того, мощность также зависит от напряжения по статической характеристике и поэтому
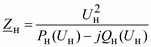. (2.54)
Нагрузка может быть представлена в виде двух схем замещения: с последовательным и параллельным соединением элементов (рис. 2.18).
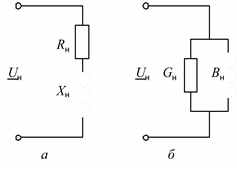
Рис. 2.18. Схемы замещения нагрузки при последовательном соединении:
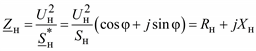, (2.55)
а при параллельном:
(2.56)
При постоянной величине заданного сопротивления или проводимости моделирование с помощью выражений (2.55) и (2.56) дает характеристики:
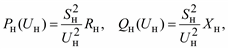
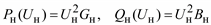. (2.57)
Моделирование постоянным сопротивлением дает обратную квад-ратичную зависимость от напряжения, а постоянной проводимостью – зависимость пропорционально квадрату напряжения. Вторая модель хорошо согласуется с моделью статической характеристики реактивной мощности нагрузки (2.52), поэтому для реактивной мощности вполне приемлема. Для активной мощности можно, например, воспользоваться линейной моделью, тогда будем иметь:
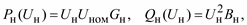(2.58)
где Gн и Bн вычислены при номинальном напряжении нагрузки.
На рис. 2.19 представлены действительные статические характеристики нагрузки (сплошные линии) и характеристики, полученные по моделям (2.58) – пунктирные линии.
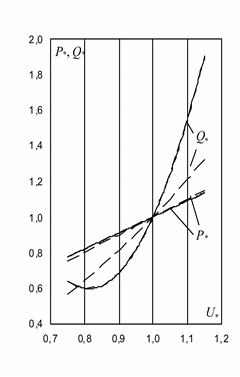
Рис. 2.19. Действительные статические характеристики нагрузки и зависимости мощностей от напряжения при моделировании нагрузки схемой замещения
Иногда в качестве данных по нагрузке бывают известны измеренные токи нагрузки. Принимая какое-либо значение коэффициента мощности нагрузки, ее можно моделировать постоянными значениями токов Iн:
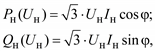(2.59)
что дает линейные статические характеристики как активной, так и реактивной мощности. Такие модели нагрузки используются в низковольтных сетях и сетях среднего напряжения.
Все математические модели электрических нагрузок, рассмотренные выше, сведены в табл. 2.6.
Таблица 2.6
Математические модели электрических нагрузок
| Математические модели | Мощность нагрузки | Примечания |
| Статические характеристики нагрузки по напряжению |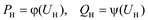 
| Получаются по данным эксперимента или подбором типовых характеристик |
| Постоянные значения мощности нагрузки |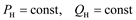 
| |
| Схема замещения: Yн = Gн – jBн = = const |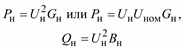 
| 
|
| Схема замещения: Zн = Rн + jXн = = const |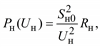 
| 
|
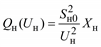
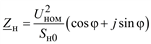
| Постоянное значение тока нагрузки: Iн = const (φ = const) |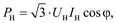 
| 
|
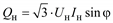
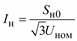
Примечание. Во всех формулах Sн0 – полная мощность нагрузки, которая может быть принята равной номинальной или максимальной мощности, а также мощности некоторого исходного или начального режима работы электроприемника или потребителя.
Защита линий
Воздушные и кабельные ЛЭП, имея большую протяженность, подвержены повреждениям в большей степени, чем другое оборудование. Особенно это относится к воздушным линиям. Поэтому для быстрого отключения они должны быть оборудованы релейной защитой, действующей на отключение.
При этом защита от замыканий на землю в сетях с заземленной нейтралью трансформаторов должна действовать на отключение, а в сетях с изолированной нейтралью – только защита от мф.кз. Замыкание на землю одной фазы в сети с изолированной нейтралью не нарушает работы потребителей. Поэтому защита от замыканий на землю выполняется с действием на сигнал для отыскания места замыкания.
Защиты линий отличаются многообразием и определяются главным образом схемой работы линий, напряжением сети и ответственностью питаемых потребителей. Для защиты ЛЭП с односторонним питанием применяются: максимальная токовая защита, токовая отсечка, токовая перечная дифференциальная защита параллельных линий, направленная токовая перечная дифференциальная защита параллельных линий. Для защиты ЛЭП с двухсторонним питанием кроме указанных выше защит применяются: максимальная направленная защита, направленная отсечка, продольная дифференциальная защита, дистанционная защита, высокочастотная защита.
Защита трансформаторов
Несмотря на то, что у трансформаторов отсутствуют движущееся и вращающееся части в процессе эксплуатации возможны и практически имеют место повреждения и нарушение нормальных режимов работы. Поэтому трансформаторы и автотрансформаторы должны оснащаться релейной защитой.
В обмотках трансформаторов могут возникать К.З. между фазами, одной или двух фаз на землю, между витками одной фазы и замыкания между обмотками. На вводах трансформаторов, ошиновок также могут возникать замыкания между фазами и на землю. Кроме указанных повреждений, в условиях эксплуатации могут происходить нарушение нормальных режимов работы трансформаторов, к которым относятся:
· прохождение через трансформатор сверхтоков при повреждении других элементов, связанных с трансформатором;
· перегрузка;
· выделение из масла горючих газов;
· понижение уровня масла, повышение его температуры.
Из вышеизложенного следует, что защита трансформаторов должна удовлетворять следующим условиям:
1. Отключать трансформатор от всех источников питания при его повреждении.
2. Отключить трансформатор от поврежденной части установки при прохождении через него сверхтоков в случаях повреждения шин или другого оборудования, связанного с трансформатором, а также при повреждении смежного оборудования и отказа защиты на нем или выключателе.
3. Подавать предупредительный сигнал дежурному подстанции при перегрузке трансформатора, выделении газа из масла, понижения уровня масла, повышении его температуры.
В соответствии с назначением для защиты трансформаторов при их повреждениях и сигнализации о нарушении нормальных режимов работы применяются следующие типы защит:
1. Дифференциальная защита – для защиты при повреждении обмоток, вводов, ошиновки трансформаторов.
2. Токовая отсечка мгновенного действия для защиты трансформатора при повреждении его ошиновки, вводов и части обмоток со стороны источника питания.
3. Газовая защита для защиты при повреждениях внутри бака трансформатора, сопровождающихся выделением газа, а также при понижении уровня масла.
4. Максимальная токовая защита, максимальная направленная защита или МНЗ с пуском минимального напряжения для защиты от сверхтоков, проходящих через трансформатор при повреждении, как самого трансформатора, так и элементов связанных с ним.
5. Защита от перегрузки, действующая на сигнал на подстанции с обслуживающим персоналом и на отключение – без обслуживающего персонала.
Кроме того, в отдельных случаях на трансформаторах устанавливаются другие виды защит.
Дата: 2019-07-30, просмотров: 349.
