4.1. Не торопись записать ответ. Просмотри (а еще лучше – проговори) все этапы решения. Проверь еще раз, нет ли у тебя ошибок в вычислениях и рассуждениях. Проверь, правдоподобен ли ответ, соответствует ли он здравому смыслу, нет ли в твоем доказательстве ссылок на сомнительные утверждения. Если все в порядке – ты просто молодец!
4.2. Не торопись записать ответ. Подумай, всегда ли решаема данная задача, какие условия можно было бы изменить и как. Может быть, ты сможешь обнаружить что-то, что может оказаться полезным при решении других задач.
4.3. Запиши ответ. Поздравляем, твоя задача решена!
Следует заметить, что приведенная схема с успехом может быть использована не только в процессе решения математической задачи, но и при решении любой проблемы, причем не только учебной. Так что работа ученика будет иметь не только учебный, но, что важнее, и развивающий и воспитывающий эффект.
Методы (приемы) работы над задачей:
- Изучение условия задачи;
- Выдвижение идеи (плана) решения;
- Поиск аналогии, сравнительные чертежи.
- Разбиение задачи на подзадачи.
- Решение одной задачи несколькими способами;
- Прием разбора готового решения;
Метод же один: метод указаний и самостоятельного поиска “мыши” в куче камней.
“Помогая ученику, учитель должен оказывать ему внутреннюю помощь, т.е. ограничиться такими подсказками, которые могли бы рождаться в сознании самого ученика, и избегать внешней помощи, т.е. давать куски решения, которые не связаны с сознанием ученика” (Д. Пойа).
Невозможно сказать, как возникает решение трудной задачи. Но ясно, что в решении велика роль происходящих в мозгу бессознательных процессов. Здесь же я буду говорить об отработке лишь элементарных приемов мышления, пользуясь тремя заповедями учителя, (по Д. Пойа):
- Старайся научить своих учеников догадываться;
- Старайся научить своих учеников доказывать;
- Пользуйся наводящими указаниями, но не старайся навязывать своего мнения насильно.
При обучении неискушенных в математике учащихся, которые привыкли решать задачи только на определенные правила, все представляет сложность.
- учащиеся не понимают, что же такое “рассуждение”, зачем вообще что-то нужно доказывать (дедуктивный аспект мышления);
- не видят логических проблем (формальнологический аспект);
- не то, что не могут найти подход к решению, а просто не осознают, что же это такое - “идея решения” (индуктивный аспект);
- они (учащиеся) не привыкли рассматривать связи между задачами (ассоциативный аспект мышления).
Для отработки элементарных навыков мышления представляется естественным выделить типы таких задач, при решении которых указанные выше аспекты применяются, так сказать, в чистом виде.
Начну с задач, служащих формированию дедуктивного аспекта мышления.
Первый тип - задачи с “естественным рассуждением”, их педагогическая роль состоит в том, чтобы приучить школьников проводить последовательную цепочку рассуждений (к чему сводится решение любой математической задачи). На первых порах следует отбирать задачи, в которых нет сколько либо необычных математических идей, такие, как простейшие логические и комбинаторные задачи, математические ребусы.
Два конкретных примера:
На острове живут рыцари, которые всегда говорят правду, и купцы, которые всегда лгут. Островитянин в присутствии другого островитянина говорит, что по крайней мере один из них лжец. Кто они?
Миша, Сережа, Дима, Валера и Костя рисовали машины:
- кто-то рисовал пожарную машину красным карандашом;
- кто-то гоночную машину синим фломастером;
- кто-то - грузовик коричневой ручкой;
- кто-то - легковую машину синим карандашом;
- кто-то - легковую машину коричневым фломастером.
Миша и Сережа рисовали карандашом. Сережа и Дима рисовали одинаковым цветом. Кто что рисовал?
Второй тип - “задачи - ловушки”, в которых напрашивающийся ответ является неверным. Их роль показать необходимость доказательств (рассуждений).
- 100 кг свежесобранных грибов имели влажность 99%. Через 2 дня их влажность составляла 98%. Сколько стали весить грибы?
- Два мальчика играли в шашки 2 часа. Сколько играл каждый из них?
- Масса петуха на двух ногах 4 кг. Какова будет масса, если петух встанет на 1 ногу.
Третий тип. Следующая ступенька в развитии дедуктивного мышления связана с формально-логическим аспектом. Его можно подчеркнуть с помощью так называемых очевидных задач, в которых ответ абсолютно очевиден (и верен), но на первых порах совершенно неясно, как же его получить.
Мама купила 4 воздушных шара: красные и голубые. Красных шаров больше, чем голубых. Сколько шаров каждого цвета купила мама?
С этого момента переходим от формально-логических и дедуктивных задач к индуктивным, которые уже непосредственно связаны с поиском идеи. И наша цель – помочь детям.
Один из древних и действенных методов обучения это “метод Сократа”, т.е. диалог с аудиторией. Искусство наставника состоит в том, чтобы задавать учащимся такие вопросы, которые они должны бы задавать сами себе. Безусловно, такой вопрос можно поставить практически к любой задаче, однако желательно, чтобы он не был прямой подсказкой.
Итак, четвертый тип задач - это “задачи с внутренним вопросом”.
а) Переложить 2 спички из числа имеющихся так, чтобы образовалась фигура, состоящая из четырех одинаковых квадратов.
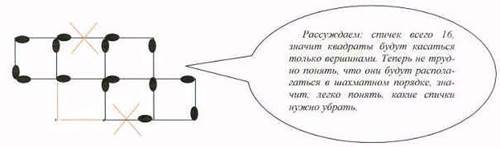
Перейдем теперь к вопросу о формировании ассоциативного аспекта мышления.
Как известно, интеллект человека во многом определяется числом задействованных связей между клетками его мозга. Естественно, что для развития математического мышления необходимо устанавливать связи между фактами, понятиями, задачами и т.д. Причем устойчивость возникшей связи зависит от того, насколько самостоятельно она была открыта. “Тем, что вы были вынуждены открыть сами, можете снова воспользоваться, когда в этом возникает необходимость” (Г. Лихтенберг).
Решение задач часто возникает по ассоциации с чем-то известным, подчеркну, что не по аналогии, а “по ассоциации”.
В этой связи представляю пятый тип задач - задачи-загадки:
- Сосчитай быстро: 012345678910.
Сколько в сумме 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 составят числа, записанные в ряд? - Сколько девочек в классе?
Если от наибольшего двузначного числа отнять числа, записанные двумя восьмерками, а к полученному числу прибавить наименьшее двузначное число, то как раз получается нужное число. Сколько девочек было в классе?
Умение воспринимать ход мысли и “читать между строк” — важная составляющая общего образования, которую можно воспитать в процессе обучения математике. Ведь математика “ум в порядок приводит”.
Задачи для самостоятельного анализа.
- Найдите все целочисленные решения уравнения:
х у = х + у. - Папа купил арбуз Д=20см, толщина корки которого составила 1см. Какой % стоимости этого арбуза оказался истраченным на корку?
- Сколькими способами можно расставить на шахматной доске 8 ладей, чтобы они не били друг друга?
- Скорый поезд вышел из Москвы в С-Петербург и шел без остановки со скоростью 60 км/ч. Другой поезд вышел ему навстречу из С-Петербурга в Москву и тоже шел без остановок со скоростью 40 км/ч. На каком расстояний будут эти поезда друг от друга за час до встречи?
Отсюда понятно, что нестандартные задачи это такие, для которых в курсе математики не имеется общих правил и положений, определяющих точную программу их решения. Такие задачи обычно включены в олимпиады
Правил решения задач нестандартного характера нет. Но великими решателями задач найдено ряд общих рекомендаций-указаний, которыми можно пользоваться при решении. Эти советы -рекомендации назовем эвристическими правилами.
Чтобы решить нестандартную задачу, надо составить (найти) план (ход) решения - не обязательно точный и полный перечень действий. Большей частью это даже не ход, а только идея, а все остальное возникает в процессе решения. Иногда оказывается, что идея не верна, и надо все начинать снова. Процесс этот не поддается точному определению, но говорить при этом о каких-то общепринятых шагах можно, хотя поиску решения задач нельзя научить, можно лишь самому научиться.
Совет 1. Распознай вид данной задачи.
Как распознать вид задачи? Первым признаком является характер требования задачи. По этому признаку выделим 3 вида задач:
- Задачи на нахождение искомого (вычислительные задачи).
- Задачи на доказательство или объяснение (верность, ложность утверждения, объяснение какого - то фактора).
- Задачи на преобразование или построение (сконструировать что -то, изменить).
Совет 2. Сведи решение к уже решаемому.
Совет прост, но практически воспользоваться им не так-то просто. Ведь нет определенных правил для такого сведения незнакомых задач к уже решенным. Однако, если внимательно, вдумчиво анализировать задачи, вдумчиво решать каждую задачу, фиксируя в своей памяти все приемы, с помощью которых были найдены решения, какими методами, способами были решены задачи, то постепенно у вас вырабатывается умение в таком сведении. Не секрет ведь, что человек, который не умеет решать стандартные задачи, не решит и нестандартную.
Один из организаторов математических олимпиад в России, известный математик Тартаковский Владимир Абрамович сравнивал поиск решения задачи с поиском (задачей) пой мать мышь, прячущуюся в куче камней. Есть два способа к этому:
- отбрасывать постепенно по камню, пока не покажется мышь;
- ходить вокруг горы и внимательно смотреть, не покажется ли хвостик; тогда хватать и вытягивать мышь из кучи.
Действительно, поиск решения напоминает поиск этой самой мыши. Живой пример такого поиска (задача о ракушках, найденных мальчиком). Ответ. Среди мальчиков нет такого, который не нашел ни одной ракушки. Так как мальчики нашли 5 ракушек, то могут быть такие варианты решения:
- 2 мальчика нашли по 1, один 3.
- 2 мальчика - по 2, третий - 1.
- Один нашел - 4, один - 1, один - ни одной.
Так как варианты 1 и 3 не соответствуют условию задачи, решением является только варианты 2: 2+2+1.
Поиск решения нестандартной задачи сводится к работе над задачами .процессуальными, которые способствуют развитию умений сравнивать, анализировать, обобщать, прогнозировать, рассуждать, планировать. Задачи на нахождение и описание процесса достижения поставленной цели при определенных условиях называются процессуальными. Ответом задач является сам процесс получения того фактора, который выступает целью деятельности.
Ценность таких задач в том, что их решение способствует формированию операционного стиля мышления, необходимого для изучения математики и информатики.
Процессуальные задачи по виду деятельности учащихся при их решении можно разделить на эвристические и алгоритмические (пошаговые). Деление это чисто условное. Эвристические процессуальные задачи вовлекают детей в творческую поисковую или частично - поисковую деятельность, содействующих развитию интеллектуальных умений.
Способы решения таких задач:
- Составление таблиц, (переливание).
- Использование рисунка и рассуждения по рисунку
- Оформление схем или блок- схем. (Задача про козу, волка и капусту).
(блок - схема - взвешивание монет).
(рисунок к задаче с велосипедами).
Такого рода задачи можно найти сколько угодно или составить. При решении учащиеся используют разные символы, образы, а ответы получают в результате рассуждений. Это и продвигает их в развитии.
Третий вид задач: преобразование или построение содержит задачу воссоздать образ изображенных предметов и различные мыслительные операции с этими образами. Очень распространены в этом виде задач со спичками (примеры на листах).
В заключении сформируем основные рекомендации для поиска решения нестандартных задач:
- Прочтя задачу, надо попытаться установить, к какому виду задач она принадлежит.
- Если вы узнали в ней стандартную задачу знакомого вида, то примените для решения общее правило.
- Если же задача нестандартная, то следует:
а) Вычленять из задачи или разбивать ее на подзадачи стандартного вида (способ разбиения), привлечь аналогию;
б) Ввести в условие вспомогательные элементы, построения;
в) Заменить задачу другой равносильной задачей (способ моделирования).
Для того, чтобы было легче понять и решить задачу, полезно предварительно построить вспомогательную модель задачи - ее схематическую запись.
Решение нестандартных задач есть искусство, которым можно владеть лишь в результате глубокого постоянного самоанализа действий по решению задач и постоянной тренировки в решении разнообразных задач.
Помните, что решение задач - есть вид творческой деятельности, а поиск решения - процесс изобретательства.
Нестандартная задача - это задача, решение которой для данного ученика не является известной цепью известных действий.
В умении решать нестандартные задачи входят моральные качества: настойчивость, терпение, воля к победе;
- Знание методов решения; знание эвристических приемов и умение избирать новые приемы решения;
- Умение пополнять полезную информацию.
Следующим важнейшим аспектом является тщательное изучение и осмысление требований задачи. Эвристическое правило “Изучи цель, поставленную задачей. Не начинай решение в слепую. Выбери направление поиска плана на решения, руководствуясь целью задачи”.
Метод указаний позволяет детям успешнее и быстрее решить задачу, но применять его нужно только тогда, когда есть полная уверенность в его полезности.
Если задача такова, что в ходе ее решения предстоит сделать слишком много указаний, то полезнее применить прием разбора готового решения.
Поиск плана решения многих задач требует у школьников так называемых комбинаторных способностей, под которыми понимают умение сделать подходящий выбор. При первой же трудности учащийся должен спросить, как он ранее преодолевал трудности, отыскать подходящую аналогию. Для этого полезно применять сравнительные чертежи, вспомогательные характеристики.
Установление сходства сразу наталкивает на плодотворные идеи.
Прием разбиения задачи на подсказки, каждая из которых решается довольно легко. (Задачи на построение 3 вид).
Метод решения одной задачи несколькими способами. Зачем он? Различные способы решения задачи дают возможность использовать те или иные теоретические положения. Это делает знания более прочными, осознанными.
Общепринятое в методике математики деление процесса решения задачи на 4 основных этапа:
- Осмысления условия задачи;
- Составление плана - выдвижение идеи, гипотезы;
- Осуществление плана решения;
- Изучение найденного решения.
СЛОВАРЬ
Что такое эвристическое оправдание при решении задачи - Это пошаговая мотивация эвристических действий в которой каждый этап доказательства должен быть мотивирован и оправдан с точки зрения предыдущего этапа т.е. убеждения в целесообразности очередного этапа решения задачи.
Синтезом каких подходов является эвристическая разработка решения задачи - Синтезом всех возможных подходов.
Что такое эвристический поиск - это системы эвристических действий, направленные на получение нового знания, разработку проблем активности и самостоятельности учащихся и внедрением проблемного обучения.
Что такое эвристическое правило - Это элементарная единица методологических средств, содержащая рекомендации по выбору возможного действия в условиях альтернативного поиска.
Что такое структура задачи? из чего состоит содержание задачи - Структура это совокупность достаточно элементарных объектов с конкретно описанной связью между ними, которая представляет однозначную организацию совокупности.
Если в заданной форме определены структурные элементы, связи между ними, а так же известные и неизвестные элементы структурных объектов.
Взаимодействие каких компонентов происходит в процессе учебного исследования - состоит из 4-х компонентов:
Объекта исследования (предмету, явления окружающей действительности, физические и социальные законы и т.п.).
Субъекта исследования (определенный студент, коллектив учащихся).
Руководителя исследования (Тьютор).
Методов исследования: экспериментального и теоретического.
Чем экспериментальные учебные исследования отличаются от теоритических –
Это самостоятельные эмпирические исследования в виде лабораторного или производственного эксперимента или в форме наблюдения, в результате которых исследователь получает новые явления и новые экспериментальные факты.
А это исследования объекта на основе имеющихся теоретических знаний в направлении, идущем от теории к идеям и гипотезам, закономерностям , законам и следствиям с возникновением на определенных этапах творческих догадок, озарений, находок.
Что такое эвристическая стратегия - возможный рациональный способ достижения цели.
Что такое эвристическая система - это система действий по поиску новой информации для достижения цели.
Какие эвристические умения можно выделить в эвристической учебно-познавательной деятельности –
умения приводить в систему знания об окружающей действительности и знания о деятельности в ней;
самостоятельное преобразование уже имеющихся данных, знаний, освоенных ранее способов деятельности и т.п.;
осуществление технологического мышления(самостоятельно определить рациональный порядок своей деятельности, выбирать наилучший способ действий);
использование научного подхода к принятию решений.
На чем основана эвристическая рациональность действий - она основана на интуиции, смутных субъективных ощущениях и не всегда достижима и контролируема в отличии от традиционной рациональности.
Каким правилом выражается основной принцип экономии деятельности - он выражается правилом: не делай при помощи больше того, что можно сделать при помощи меньшего.
Наиболее важные принципы обучения эвристической деятельности - к ним можно отнести принцип активности и стимулирования изучения и принцип чередования логической и эвристической деятельности.
Что такое правдоподобное эвристическое рассуждение - это рассуждение основанное, на информации, полученной в результате эвристической деятельности, достоверность которой не доказана и не опровергнута.
Литература:
- Фридман Л.М. Теоретические основы обучения математике: Учебное пособие. – изд. 2-е, испр. и доп. – М.: Едиториал УРСС, 2005. – 248 с.
- Мугаллимова С.Р. О видах эвристических приемов // Омский научный вестник – 2006 – №9. – С. 107-109.
- Пойа Д. Как решать задачу. – Львов. Журнал “Квантор”, 1991. – 215 с.
- Уфнаровский В.А. Математический аквариум. – Ижевск: Ижевская республиканская типография, 2000 – 216 с.
Кружок "Эвристические задачи". 2-й класс
Задача: Развивать ум, волю, чувства детей, как основу усвоения знаний, умений, навыков.
Цели:
- Изучить уровень способностей учеников поступающих в 2 класс.
- Выявить слабые места в интеллектуальном развитии младших школьников.
- Оказать помощь детям в развитии памяти, внимания, зрительного восприятия, творческого мышления, языкового чутья, фантазии.
- Учить решать эвристические задачи.
- Развивать интеллект и познавательную деятельность учеников.
ПРОГРАММА
1. Что такое интеллект?
2. Головоломки на внимание.
3. Головоломки на внимание.
4. Ребусы.
5. Анаграммы.
6. Анаграммы
7. Аналогии.
8. Головоломки.
9. Кроссворды.
10. Перевертыши.
11. Игры Деда Буквоеда.
12. Игры Деда Буквоеда.
13. Буквенные логические цепочки.
14. Логические цепочки.
15. Задачи шутки.
16. Тестирование учащихся в конце года. – 2 ч
Кружок помогает формировать интеллектуальные способности ученика:
- развивать гибкость и логику мышления;
- хорошую память;
- устойчивое внимание
- умение формировать понятия;
- развивать речевые способности;
- цепкое пространственное восприятие, т. е. интеллект.
Занятие № 1.
Тема: Что такое интеллект?
Цель: Познакомить с понятием “интеллект”; пробудить желание стать умными, грамотными; познакомить с различными видами упражнений для мозга.
Ход занятия:
 1. Игра на внимание.
1. Игра на внимание.
– Смотри на квадрат 10 секунд.
– Закрой глаза на 10 секунд.
– Меняю 2 фигуры местами.
Что изменилось? (повторяю 3-5 раз).
Беседа об интеллекте.
– Кому удалось запомнить расположение фигур без труда?
– Кому не удалось?
– Зачем человеку нужна память?
– Можно ли развивать, улучшать свои умственные способности?
Ум - удивительная особенность человека. Мы не можем его потрогать, увидеть, услышать, но он всегда с нами и создает нашу жизнь. Чтобы быть умным, надо выполнять умственные операции для массажа своего мозга. Мозг это мышцы, а они должны двигаться, чтобы не быть вялыми, дряблыми.
Ум, рассудок, разум, мыслительные способности, т. е.способность к обучению – это интеллект. Любой человек может повысить или понизить свои интеллектуальные способности.
Что может снизить интеллект человека?/ курение, травмы, алкоголизм, болезни./
Какие упражнения повышают умственные способности?
Развивающие упражнения:
РЕБУСЫ
| У | З, | О | Показываю сложные ребусы. |
| П А | , | З Ж | |
| Л И | 100 К |
ГОЛОВОЛОМКИ
| 2, . | 4, | 6, | 8, | … | Продолжи ряд на 1число. |
| 1, | 3, | 5, | 7, | …. |
АНАГРАММЫ сел /лес/, сорт /трос/ сукно /конус/ сосна /насос/
ШАРАДЫ Число и нота рядом с ним,
Да букву припиши согласную,
А в целом мастер есть один,
Он мебель делает прекрасную. /столяр/
С “с” - на дереве расту,
С “ж” - по дереву ползу. /сук, жук/
ПЕРЕВЕРТЫШИ: У лип Алеша нашел пилу.
КРОССВОРДЫ:

ИГРЫ В СЛОВА: /придумай слово на последний звук, на 1 звук, на 3 звук…/
ЗАГАДКИ: /провести конкурс загадок/
– Где, по-вашему, можно найти интеллектуальные задачи? (выставка книг, газет, сборников, …)
Подводим итог занятия.
– У кого больше жетонов? /давались за каждое правильное задание./
– Называется “ЭРУДИТ”.
Занятие №2
Тема: Головоломки на внимание.
Цель: Познакомить с решением головоломок, развивать зрительное восприятие, наблюдательность, учить сравнивать, находить общее, различия.
Ход занятия.
 1. Игра на внимание.
1. Игра на внимание.
Смотрим 10 секунд.
Закрываем на 10 секунд глаза.
Что изменилось?/повторяю 3-4 раза/
Вставь нужную фигуру.
Какой фигурки не хватает? Докажи.
Кто не согласен? Докажи.
Чем кроме формы фигурки отличаются друг от друга?

Работа в паре.
Дети находят ответ, обсуждая его с соседом.
Ответ зарисовывают в тетрадь.
Проверяем, сверяя ответы.

Индивидуальная работа.
Раздаю каждому свою головоломку. Ответы выбирают на листе с готовыми вариантами. Не справился, помогает одноклассник-консультант.
Составь сам.
Раздаю картинки из вкладышей в букварь.
Рисуем сетку из 9 квадратов.
Задание: 1. Составь головоломку из картинок.
2. Разгадай задание у соседа по парте.
3. Оцени, как он разгадал твое задание.
4. За правильный ответ вручи ему жетон.
6. Итог занятия. Считаем жетоны. Можно сделать переходящую медаль “ЭРУДИТ”.
Занятие №3
Тема: Головоломки на внимание.
Цель: Развивать зрительное восприятие, внимание, логическое мышление: закрепить знание печатных букв.
Ход занятия.
Игра на внимание.
“Цифра-буква” Дети по очереди называют цифру-букву. Ошибся - выбываешь из игры.
Дата: 2019-05-29, просмотров: 359.