Определение. Касательной плоскостью к поверхности в точке 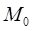 называется плоскость, содержащая все касательные к кривым, принадлежащим поверхности и проходящим через точку
называется плоскость, содержащая все касательные к кривым, принадлежащим поверхности и проходящим через точку 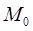 .
.
Нормаль к поверхности – это прямая, перпендикулярная касательной плоскости и проходящей через точку касания 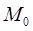 .
.
Уравнение любой плоскости, проходящей через заданную точку 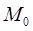 имеет вид:
имеет вид:  , где
, где 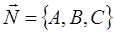 - нормальный вектор, перпендикулярный к плоскости.
- нормальный вектор, перпендикулярный к плоскости.  - точка касания. Уравнения любой прямой, проходящей через точку
- точка касания. Уравнения любой прямой, проходящей через точку 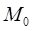 :
:  - где m, n, p – координаты направляющего вектора прямой
- где m, n, p – координаты направляющего вектора прямой 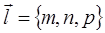 . Для нормали в качестве направляющего вектора можно взять вектор
. Для нормали в качестве направляющего вектора можно взять вектор 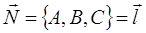 .
.

 Если уравнение поверхности имеет вид
Если уравнение поверхности имеет вид 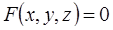 , то нормальный вектор к ней в точке
, то нормальный вектор к ней в точке 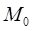 :
: 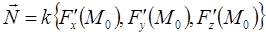 .
.
Тогда уравнение касательной плоскости: 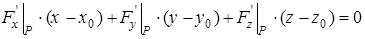 .
.
Уравнения нормали к поверхности в точке  :
: 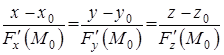 .
.
Если уравнение поверхности имеет вид  , то
, то  . (Это уравнение можно переписать в виде
. (Это уравнение можно переписать в виде 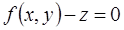 и положить
и положить 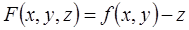 .)
.)
Пример 12.9. Составим уравнение касательной плоскости и уравнения нормали к поверхности 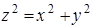 в точке
в точке 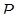
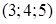 .
.
Решение. Обозначим через 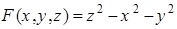 . Найдем значения частных производных в точке
. Найдем значения частных производных в точке 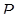 :
: 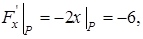
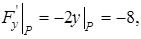
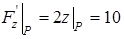 . Подставим полученные результаты в уравнения касательной плоскости и нормали. Ответ: уравнение касательной плоскости имеет вид
. Подставим полученные результаты в уравнения касательной плоскости и нормали. Ответ: уравнение касательной плоскости имеет вид 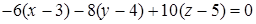 или
или 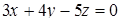 , а уравнения нормали -
, а уравнения нормали -  .
.
Пример 12.10. Составим уравнения плоскостей, касательных к поверхности 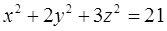 и параллельных плоскости
и параллельных плоскости 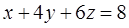 .
.
Решение. Уравнение касательной плоскости имеет вид: 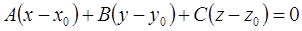 .
.
Так как она параллельна плоскости 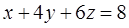 , то её нормальный вектор
, то её нормальный вектор 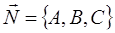 коллинеарен нормальному вектору этой плоскости
коллинеарен нормальному вектору этой плоскости 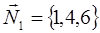 . Необходимо найти точку касания
. Необходимо найти точку касания 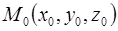 . Координаты этой точки фигурируют при отыскании нормального вектора
. Координаты этой точки фигурируют при отыскании нормального вектора 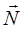 к поверхности. Рассмотрим уравнение поверхности в виде
к поверхности. Рассмотрим уравнение поверхности в виде 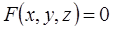 , где
, где 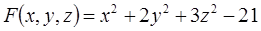 . Вычислим частные производные функции
. Вычислим частные производные функции 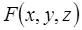 в точке касания
в точке касания 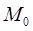 :
:
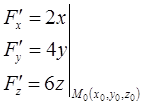
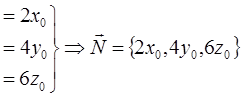
Из условия коллинеарности векторов 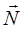 и
и 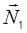 следует пропорциональность их координат. Мы получим два уравнения с тремя неизвестными:
следует пропорциональность их координат. Мы получим два уравнения с тремя неизвестными: 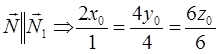
Третье уравнение получим, если учтём, что точка 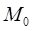 должна принадлежать поверхности, а, следовательно, её координаты обращают уравнение поверхности в тождество:
должна принадлежать поверхности, а, следовательно, её координаты обращают уравнение поверхности в тождество: 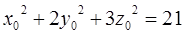
Для нахождения неизвестных 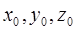 решаем систему:
решаем систему: 
Найдём две точки касания: 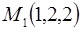 и
и  .
.
Составим искомые уравнения касательных плоскостей с нормальным вектором  , подставляя координаты точек и вектора в уравнение плоскости.
, подставляя координаты точек и вектора в уравнение плоскости.
Ответ: касательная плоскость в точке 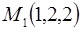 имеет уравнение
имеет уравнение 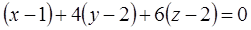 , а в точке
, а в точке  -
-  .
.
Занятия 14-15 . Экстремум функции нескольких переменных. Условный экстремум функции двух переменных. Наибольшее и наименьшее значение функции 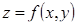 в замкнутой ограниченной области.
в замкнутой ограниченной области.
Ауд.: [3] 7.187–7.195 (неч.), 7.201, 7.205, 7.214.
Дома: [3]: 7.187–7.195 (четн.), 7.202–7.204, 7.210–7.213.
Часть 1. Экстремум функции нескольких переменных.
Определение. Точка  называется точкой строгого локального максимума (минимума) функции
называется точкой строгого локального максимума (минимума) функции 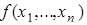 , если существует окрестность
, если существует окрестность  такая, что для любого
такая, что для любого 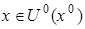 :
:  (
(  ).
).
Определение. Точки локального максимума и минимума функции нескольких переменных называются точками локального экстремума данной функции.
Необходимое условие локального экстремума. Если 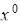 - точка локального экстремума функции
- точка локального экстремума функции 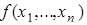 , которая является непрерывной в этой точке и имеет в ней конечные частные производные
, которая является непрерывной в этой точке и имеет в ней конечные частные производные 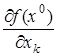 ,
, 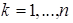 , то
, то 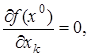
 .
.
Определение. Точки функции 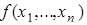 , в которых
, в которых 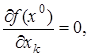
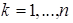 , называются стационарными точками функции.
, называются стационарными точками функции.
Достаточное условие локального экстремума. Пусть 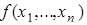 имеет в области
имеет в области  непрерывные частные производные до 2 порядка включительно и точка
непрерывные частные производные до 2 порядка включительно и точка  - стационарная точка этой функции. Тогда если дифференциал второго порядка
- стационарная точка этой функции. Тогда если дифференциал второго порядка 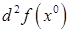 знакоопределён, то точка
знакоопределён, то точка  является точкой локального экстремума. Причём, если
является точкой локального экстремума. Причём, если 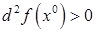 , то это точка локального минимума, а если
, то это точка локального минимума, а если  , то это точка локального максимума.
, то это точка локального максимума.
Заметим, что 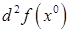 является квадратичной формой
является квадратичной формой 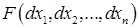 , и её знакоопределённость можно исследовать, используя критерий Сильвестра. Матрица этой квадратичной формы
, и её знакоопределённость можно исследовать, используя критерий Сильвестра. Матрица этой квадратичной формы 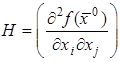 (матрица Гессе). В частности, для функции
(матрица Гессе). В частности, для функции  план исследования по достаточному признаку существования точек локального экстремума выглядит следующим образом.
план исследования по достаточному признаку существования точек локального экстремума выглядит следующим образом.
Пусть  имеет в области
имеет в области 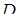
 непрерывные частные производные до 2 порядка включительно и точка
непрерывные частные производные до 2 порядка включительно и точка 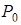
 стационарная точка этой функции. Обозначим
стационарная точка этой функции. Обозначим 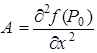 ,
,  ,
, 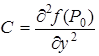 ,
, 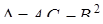 . Тогда матрица Гессе имеет вид
. Тогда матрица Гессе имеет вид 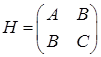 и её главные миноры
и её главные миноры 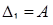 и
и 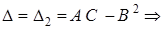
1) если  , то
, то  является точкой локального минимума;
является точкой локального минимума;
2) если 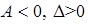 , то
, то 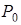 является точкой локального максимума;
является точкой локального максимума;
3) если 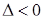 , то
, то 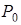 не является точкой локального экстремума;
не является точкой локального экстремума;
4) если  , то требуются дальнейшие исследования.
, то требуются дальнейшие исследования.
Пример 14.1. Исследуем на экстремум функцию 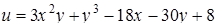 .
.
Решение. Найдем стационарные точки, используя необходимые условия локального экстремума.

Получили 4 стационарные точки 
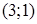 ,
, 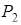
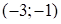 ,
, 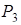
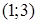 ,
, 
 . Применим теорему о достаточном условии локального экстремума для каждой точки (см. план). Вычислим частные производные
. Применим теорему о достаточном условии локального экстремума для каждой точки (см. план). Вычислим частные производные  ,
, 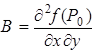 ,
,  , где
, где  .
.
В точке 
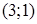 имеем
имеем 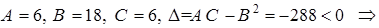 точка
точка  не является точкой экстремума.
не является точкой экстремума.
В точке 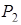
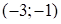 имеем
имеем  точка
точка  не является точкой экстремума.
не является точкой экстремума.
В точке 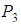
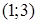
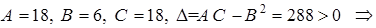 точка
точка  - точка локального минимума.
- точка локального минимума.
В точке 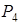
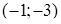
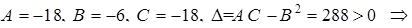 точка
точка 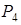 - точка локального максимума. Вычислим экстремальные значения функции.
- точка локального максимума. Вычислим экстремальные значения функции. 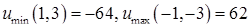 .
.
Часть 2 . Условный экстремум функции двух переменных.
Рассмотрим следующую задачу. Требуется найти максимум или минимум функции 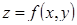 , достигнутый при условии, что её аргументы связаны уравнением
, достигнутый при условии, что её аргументы связаны уравнением 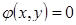 (уравнение связи).
(уравнение связи).
Если функции 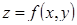 соответствует некоторая поверхность, то в этой задаче требуется найти точки, которые, во-первых, принадлежат линии пересечения поверхности
соответствует некоторая поверхность, то в этой задаче требуется найти точки, которые, во-первых, принадлежат линии пересечения поверхности 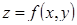 и цилиндра, параллельного оси OZ, уравнение которого
и цилиндра, параллельного оси OZ, уравнение которого  , и, в которых, во-вторых, функция
, и, в которых, во-вторых, функция 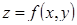 принимает экстремальные значения.
принимает экстремальные значения.
План решения задачи.
Составляется «функция Лагранжа»:  , где λ – некоторый множитель, и решается задача о нахождении обычного экстремума этой функции.
, где λ – некоторый множитель, и решается задача о нахождении обычного экстремума этой функции.
1. Точки, где возможен экстремум, находятся из необходимых условий экстремума, к которым надо присоединить уравнение связи:
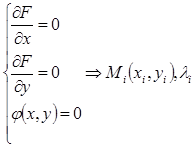
2. Для выяснения наличия или отсутствия экстремума в найденных точках необходимо воспользоваться достаточным признаком экстремума. Возможны следующие варианты.
а) Можно, как в задаче о безусловном локальном экстремуме, составить дискриминант 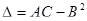 , где
, где  ,
, 
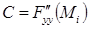 Затем сделать соответствующие выводы:
Затем сделать соответствующие выводы:
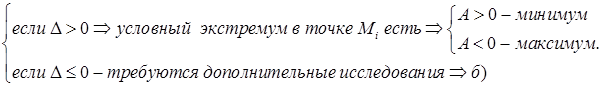
б) Можно поступить иначе - составить определитель третьего порядка
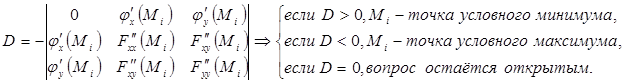
в) Наконец, можно вопрос о наличии условного экстремума решить, рассмотрев второй дифференциал функции Лагранжа в точке 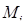 , т. е.
, т. е.
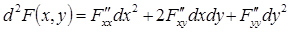 , учтя при этом, что
, учтя при этом, что 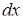 и
и  связаны между собой уравнением
связаны между собой уравнением 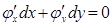 (вычислен дифференциал левой и правой части уравнения связи
(вычислен дифференциал левой и правой части уравнения связи  ), где
), где  и
и  не обращаются одновременно в ноль. Тогда
не обращаются одновременно в ноль. Тогда 

Пример 14.2. Найдём условные экстремумы функции 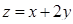 при условии
при условии  .
.
Геометрически это выглядит следующим образом. Наклонная плоскость пересекается круговым цилиндром. В пересечении получается наклонный эллипс, на котором имеются точки условного экстремума (см. рис. 10).
Решение. (См. план решения задачи) Составляем функцию Лагранжа 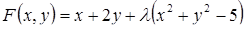 . Находим точки, где возможен условный экстремум этой функции, решая соответствующую систему
. Находим точки, где возможен условный экстремум этой функции, решая соответствующую систему


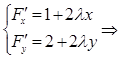
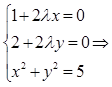
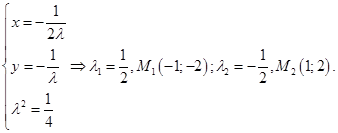
2. Находим производные второго порядка от функции Лагранжа и используем достаточное условие. а)
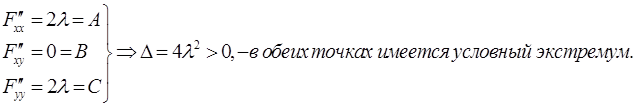
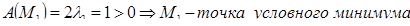 ,
,
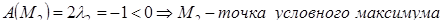 .
.
Ответ: 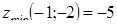 ,
,  .
.
Пример 14.3. Найдём точки экстремума функции 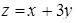 при условии
при условии  .
.
Решение. Выпишем функцию Лагранжа 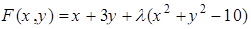 .
.
Найдем стационарные точки функции Лагранжа решив систему 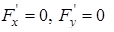 , то есть
, то есть
 .
.
Получим две точки 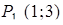 при
при 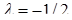 и
и 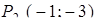 при
при  .
.
Используем способ, в котором исследуется знак дифференциала второго порядка функции Лагранжа (см. план, пункт в)). 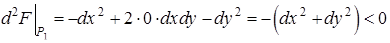 . Вывод, точка
. Вывод, точка 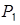 является точкой условного максимума.
является точкой условного максимума.
Аналогично, в точке 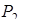 получаем
получаем 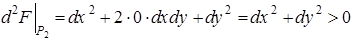 , откуда следует, что точка
, откуда следует, что точка  является точкой условного минимума. Вычисляем значения функции в точках локальных условных экстремумов.
является точкой условного минимума. Вычисляем значения функции в точках локальных условных экстремумов. 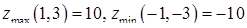
Часть 3 . Наибольшее и наименьшее значение функции 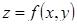 в замкнутой ограниченной области.
в замкнутой ограниченной области.
Одно из свойств непрерывной функции заключается в том, что в замкнутой ограниченной области D множество числовых значений функции имеет точные верхнюю и нижнюю границы, причём обе они являются значениями функции по крайней мере в одной точке области. Эти значения называются наибольшим и наименьшим значениями функции в области D.
Обозначим наибольшее и наименьшее значения функции 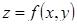 в замкнутой области D соответственно через M и m. Эти значения могут достигаться функцией либо во внутренних точках области D (в точках экстремума), либо на границе области (и тогда они являются условными экстремумами функции).
в замкнутой области D соответственно через M и m. Эти значения могут достигаться функцией либо во внутренних точках области D (в точках экстремума), либо на границе области (и тогда они являются условными экстремумами функции).
План решения задачи о нахождении наибольшего и наименьшего значений непрерывной функции 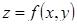 в замкнутой области D, граница которой имеет уравнение
в замкнутой области D, граница которой имеет уравнение 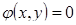 .
.
1. Находим стационарные точки (точки, где  и
и 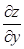 обращаются в нуль), принадлежащие области D .
обращаются в нуль), принадлежащие области D .
2. Находим точки, где возможен условный экстремум функции 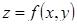 при условии
при условии 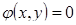 на каждом участке границы.
на каждом участке границы.
3. Вычисляем значения функции во всех найденных точках, а также в точках пересечения отдельных участков границы, если таковые имеются. Из полученных значений выбираем наибольшее и наименьшее.
Пример 14. 4. Определить наибольшее и наименьшее значение функции 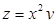 в области
в области 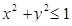 .
.
Решение. (См. план решения задачи)
1. Находим стационарные точки заданной функции, принадлежащие рассматриваемой области: 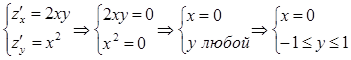
2. Составляем функцию Лагранжа:  .
.
Находим её стационарные точки: 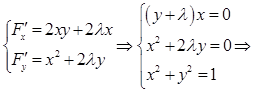
| |

3. Вычисляем значения функции во всех полученных точках. 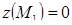 ,
,  ,
, 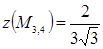 ,
, 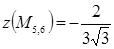 ,
, 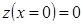 . Выбираем из этих значений наибольшее и наименьшее.
. Выбираем из этих значений наибольшее и наименьшее.
Ответ:наибольшее значение функции 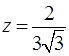 достигается в точках ,
достигается в точках ,
наименьшее значение 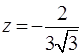 – в точках
– в точках 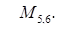
Дата: 2019-05-28, просмотров: 395.