Уравнение 2- ого порядка 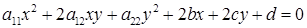 определяет на плоскости  некоторую кривую 2 – ого порядка (Это может быть эллипс, гипербола, парабола или случаи их вырождения). Чтобы построить кривую, необходимо её уравнение привести к каноническому виду и выяснить, в какой новой системе координат оно такой вид имеет. Причём для построения необходимо, чтобы новая система была прямоугольной декартовой системой .

Часть слагаемых в этом уравнении есть квадратичная форма  с матрицей 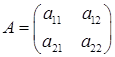 в ортонормированном базисе .

Существует ортогональное линейное преобразование, которое приводит квадратичную форму к каноническому виду 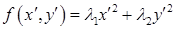 в новом ортонормированном базисе 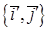. При этом линейная связь между старыми и новыми координатами такова, что 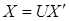, где  - матрица преобразования, элементами столбцов которой являются координаты собственных ортонормированных векторов матрицы . Выразив старые переменные 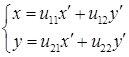 и подставив их вместе с новой квадратичной формой в уравнение (8.1), получим уравнение вида . Если теперь выделить полные квадраты, то получится каноническое уравнение одной из известных кривых в прямоугольной системе координат 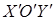 с базисом 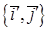, состоящим из собственных ортонормированных векторов матрицы .

Если 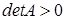,   уравнение соответствует кривой эллиптического типа, если , то  кривой гиперболического типа, если 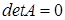, то уравнение соответствует кривой параболического типа.

Пример 7.3. Построим кривую, заданную уравнением .

Решение. Выпишем квадратичную форму, соответствующую части уравнения . Приведём её к каноническому виду ортогональным преобразованием, которое исходный ортонормированный базис преобразует в новый ортонормированный базис из собственных векторов матрицы . Это преобразование позволит построить кривую в новой прямоугольной системе координат.

Составим матрицу квадратичной формы: .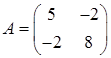

Определитель Кривая эллиптического типа.

Составим характеристическое уравнение и вычислим собственные значения матрицы:

. Так как , собственные векторы, им соответствующие, ортогональны.

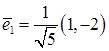 и 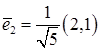 - нормированные собственные векторы, соответствующие и 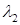. Эти векторы образуют новый ортонормированный базис, в котором матрица квадратичной формы принимает канонический вид , а её матрица принимает диагональный вид: .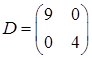

Матрица перехода к новому базису составляется из координат новых базисных векторов: . Связь между новыми и исходными координатами осуществляется с помощью матрицы перехода по формуле: 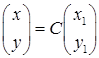, откуда получим: .

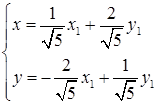Подставим в исходное уравнение кривой полученные выражения старых переменных через новые, а также заменим квадратичную форму: .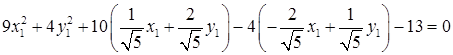

Приведём подобные слагаемые, выделим полные квадраты и получим каноническое уравнение эллипса в новой системе координат: 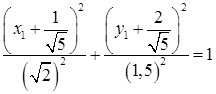. Чтобы построить эллипс в исходной системе координат, на координатной плоскости проведём новые координатные оси: ось  в направлении собственного вектора 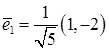, и ось   в направлении собственного вектора 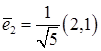. В новой системе строим эллипс с центром симметрии в этой системе 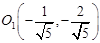, с полуосями  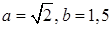(см. рис. 2).

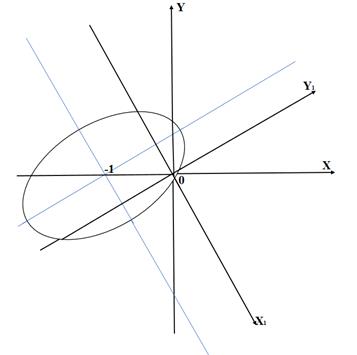
Рис.2. Эллипс, заданный уравнением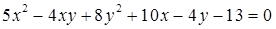

Пример 7.4. Исследуем уравнение и построим кривую: .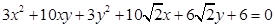

Решение. Выпишем квадратичную форму, соответствующую уравнению:

.

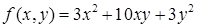Составим матрицу квадратичной формы: .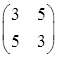

Исследуем определитель квадратичной формы: кривая гиперболического типа.

Составим характеристический полином и вычислим собственные числа квадратичной формы:

, .

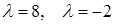Собственные (нормированные) векторы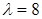: для : , для : .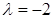

Из собственных векторов составим базис, в котором квадратичная форма приобретает канонический вид: , а её матрица становится диагональной: . Матрица перехода к новому базису: .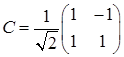

Связь между новыми и исходными координатами осуществляется с помощью матрицы перехода по формуле: 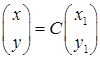, откуда получим:             , .

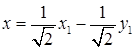Подставим в исходное уравнение кривой данные выражения, а также заменим квадратичную форму каноническим видом: .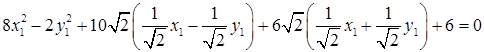

Приведём подобные слагаемые, выделим полные квадраты. Окончательно получим уравнение в каноническом виде: .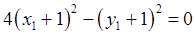

Это случай вырождения случай гиперболы в  пару пересекающихся прямых .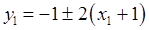

Чтобы построить полученные прямые, на координатной плоскости проведём новые координатные оси: ось OX_1, в направлении собственного вектора 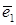, и ось OY_1, в направлении собственного вектора .

Центра пересечения прямых отмечаем уже в новой системе координат, и строим прямые (см. рис.3).

Рис. 3. Вырожденный случай гиперболы – пара пересекающихся прямых.

Аналогично приводятся к каноническому виду и строятся поверхности второго порядка.

Пример 7.5. Привести к каноническому виду уравнение и построить поверхность: .

Решение. Выпишем квадратичную форму, соответствующую уравнению: .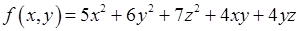

Матрица квадратичной формы имеет вид: .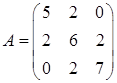

Составим характеристический многочлен  и вычислим собственные значения  квадратичной формы: .

Найдём собственные ортонормированные  векторы. для 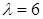: 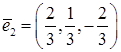,    для : ,   для : .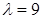

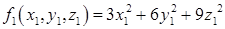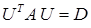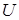Собственные ортонормированные  векторы образуют базис, в котором квадратичная форма имеет  канонический вид:  , а её матрица становится диагональной: . (В качестве проверки можно вычислить произведение , где  - матрица перехода к новому базису, имеющая вид ).

Связь между новыми и исходными координатами осуществляется с помощью матрицы перехода по формуле: , откуда получаем

, , .

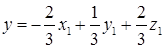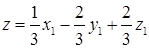Подставим в исходное уравнение кривой данные выражения, а также заменим квадратичную форму каноническим видом: .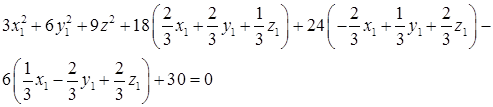

Упростим уравнение, выделим полные квадраты и приведём его к каноническому виду:

Мы получили уравнение смещённого эллипсоида. Координаты центра симметрии эллипсоида в новой системе координат O’(1,-2,-1).

Чтобы построить эллипсоид, проведём новые координатные оси так, что  ось 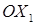  пойдёт в направлении собственного вектора 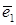, ось  - в  направлении собственного вектора 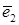, а ось  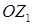-  в направлении собственного вектора .

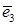Искомый эллипсоид см. на рис. 4

Рис.4. Эллипсоид, заданный уравнением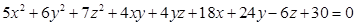

Самостоятельно решите задачи 4.226, 4.228, 4.231 [3]

Занятие 9 . Контроль по модулю 1.