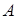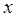Определение.  Число   называется пределом функции при стремлении  к 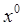, если функция определена в некоторой проколотой окрестности  и для любого 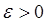 существует такое 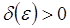, что для всех 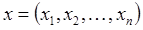, удовлетворяющих неравенству: , выполняется неравенство: .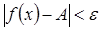

Пример 10.4. Вычислим .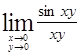

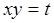Решение. При непосредственной подстановке получаем неопределённость типа . В результате замены  преобразуем предел функции двух переменных в известный предел функции одной переменной, а именно .

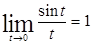Ответ: 1.

Пример 10.5. Вычислим .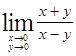

Решение. При непосредственной подстановке получаем неопределённость типа . Заметим, что если этот предел существует, то он не должен зависеть от того, как точка 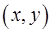стремится к точке 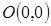. Вычислим этот предел при условии, что точка  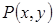стремится к  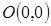вдоль оси OX, т. е. при .

Тогда .

Теперь вычислим этот предел при условии, что точка 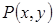 стремится к  вдоль оси OY, т. е. при . Тогда

Оказалось, что результат зависит от направления подхода точки 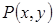 к .

Ответ: предел не определён.

Пример 10.6. Вычислим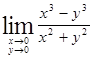

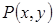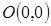Решение. Непосредственная подстановка даёт неопределённость типа . Вычислим этот предел при стремлении точки  к  вдоль оси OX и вдоль оси OY.

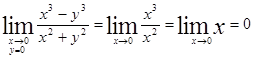и

То, что эти пределы совпали, не гарантирует существования предела, так как необходимо учесть все возможные направления стремления точки 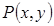 к . Рассмотрим множество прямых, проходящих через точку 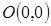 и вычислим данный предел при условии, что точка  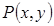стремится к  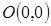по любой из них. Тогда  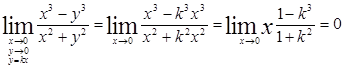при любом значении k. Ответ: 0.

Определение. Функция 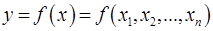 называется непрерывной в точке , если она определена в этой точке, существует  и он равен значению функции в этой точке .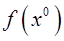

Определение. Функция  называется непрерывной на множестве, если она непрерывна в каждой точке этого  множества.

Определение. Точкой разрыва функции 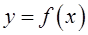 называется внутренняя или граничная точка области определения ФНП, в которой нарушено хотя бы одно из условий непрерывности.

Если точки разрыва образуют линию, то она называется линией разрыва. Если точки разрыва образуют поверхность, то она называется поверхностью разрыва. Если у точки разрыва существует окрестность, в которой нет других точек разрыва, то такая точка называется изолированной точкой разрыва.

Пример 10.7. Найдём и построим на плоскости XOY точки разрыва функции .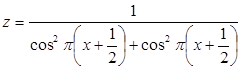

Решение. Данная функция не определена там, где .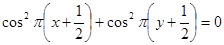

.

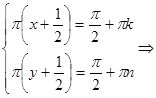
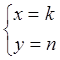Ответ: Точки разрыва ФНП - точки 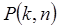, где 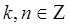(см. рис.9).

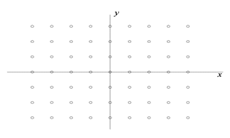                                                                                  Рис.9. Точки разрыва данной функции.

Занятие 11 . Частные производные 1-го порядка ФНП. Частные производные высших порядков ФНП. Дифференциал первого и второго порядка ФНП.

Ауд.:[3]: 7.57, 7.60, 7.61, 7.63, 7.66, 7.87, 7.89, 7.91, 7.103, 7.105.

Дом: [3] 7.56, 7.58, 7.59, 7.62, 7.64, 7.67, 7.88, 7.90, 7.92, 7.102, 7.107.