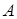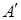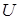Если в базисе 𝔅 квадратичная форма имеет матрицу , а в базисе 𝔅′  - матрицу , и   – матрица перехода от базиса 𝔅 к базису 𝔅′, то связь между матрицами выражается формулой .

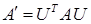Пример 6.3. Определить, как будет выглядеть матрица квадратичной формы 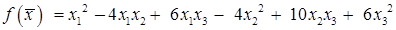 в новом базисе, если связь между координатами вектора в новом базисе  и его  координатами в исходном  базиса 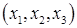задана формулами: .

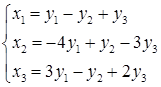Решение. Составим матрицу квадратичной формы в исходном базисе: .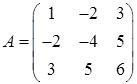

Чтобы получить матрицу перехода из исходного базиса к новому, запишем систему уравнений, задающих связь между координатами, в матричной форме:

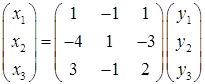. При переходе от базиса 𝔅 к базису 𝔅′, имеет место формула, связывающая координаты вектора в этих двух базисах: . Откуда следует, что матрица перехода имеет вид .

Вычислим матрицу квадратичной формы в новом базисе:

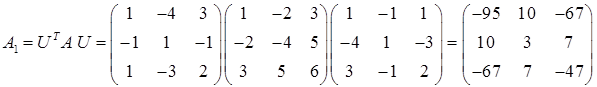. И теперь составим саму  квадратичную форму в новом базисе: .                                      Часть 3. Знакоопределённость квадратичной формы, критерий Сильвестра.

Определение. Квадратичная форма 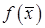 называется положительно определенной, если ее значения положительны для любого ненулевого вектора:  для .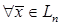

Квадратичная форма 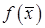называется отрицательно определенной, если ее значения отрицательны для любого ненулевого вектора:  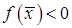для .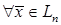

Квадратичная форма 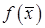 называется знаконеопределенной (знакопеременной), если она принимает и положительные, и отрицательные значения.

 Пусть 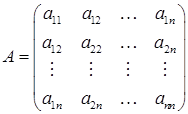 - матрица квадратичной формы. Главными минорами этой матрицы называют миноры, последовательно окаймляющие элемент 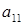, т.е. , , …, .

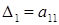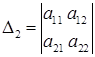Критерий Сильвестра. Для того, чтобы квадратичная форма была положительно определенной, необходимо и достаточно, чтобы все главные миноры её матрицы были положительны: Δ₁ > 0, Δ₂ > 0, …, Δ_n > 0.

Для того, чтобы квадратичная форма была отрицательно определенной, необходимо и достаточно, чтобы знаки главных миноров её матрицы чередовались так, что  Δ₁ < 0, Δ₂ > 0, Δ₃ < 0, Δ₄ > 0, …, (-1) ⁿΔ_n > 0. То есть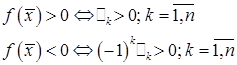

Если для невырожденной квадратичной формы не выполнено ни одно из этих условий, форма знакопеременна.

Пример 6.4. Исследовать на знакоопределённость квадратичную форму .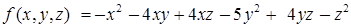

Решение. Составим матрицу данной квадратичной формы 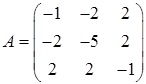. Вычислим её главные миноры. 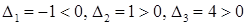. Условия знакопостоянства не выполняются, следовательно, форма знакопеременная.

Пример 6.5. Исследуем знакоопределённость квадратичной формы 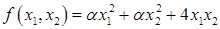в зависимости от значения .

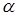Решение. Составим матрицу квадратичной формы и вычислим её главные миноры.

.  

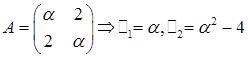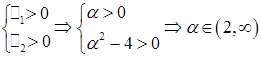Из критерия Сильвестра следует, что                                                                 , если                                                                                                                 и 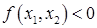, если .

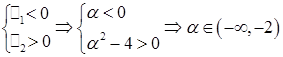Ответ: квадратичная форма положительно определенная при 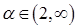, отрицательно определённая при  и знаконеопределенная для .

Решить задачи 4.218, 4.220, 4.222, 4.224. [3]

Занятия 7-8 .  Приведение квадратичной формы к каноническому виду методом Лагранжа и ортогональным преобразованием. Приведение кривых и поверхностей второго порядка к каноническому виду.

Ауд.:  [3], гл. 4: 4.210, 4.211, 4.213, 4.215, 4.226, 4.228, 4.231 Дома:  [3], гл. 4: 4.212, 4.214, 4.216, 4.227, 4.229, 4.230