Аннотация. В составе данного модуля изучаются основные понятия раздела математического анализа - функции нескольких переменных: предел, непрерывность, градиент, линии и поверхности уровня, а также раздел дифференциального исчисления функций нескольких переменных. Приведены краткие теоретические сведения, подробно разобраны типовые примеры и задачи.

Занятие 10 . Область определения ФНП. Линии и поверхности уровня. Предел и непрерывность ФНП.

Ауд.: [3]: 7.6, 7.8, 7.10, 7.19, 7.21, 7.32, 7.35, 7.44, 7.46, 7.50, 7.55.

Дом:: [3] 7.7, 7,9, 7.13, 7.20,7.33, 7.34, 7.45, 7.47, 7.51.

Часть 1. Область определения ФНП.

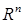Определение. Множество упорядоченных наборов из n действительных чисел , для которых определены линейные комбинации и скалярное произведение, называется точечным евклидовым арифметическим n – мерным пространством , а наборы  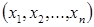называются его точками  или 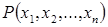. Действительные числа  называются координатами точки. Точку 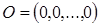 называют началом отсчёта или началом координат.

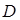Определение. Если в пространстве  определён закон, по которому каждой точке  некоторой области  этого пространства ставится в соответствие единственное действительное значение переменной 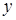, то этот закон называется функцией n переменных и обозначается .

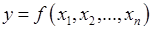Множество D называется областью определения функции, а множество
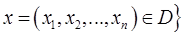- областью значений функции.

Пример 10.1. Найдём область определения функции .

Решение. Областью определения D данной функции является множество точек  плоскости XOY, таких, что их координаты удовлетворяют неравенству 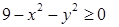.То есть 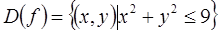. Это точки, принадлежащие кругу с центром в начале координат, радиус которого равен 3.

Часть 2 . Линии и поверхности уровня.

Определение. Линией уровня функции двух переменных 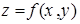 называется множество точек плоскости 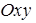, в которых функция сохраняет постоянное значение z=C.

Определение. Поверхностью уровня функции трёх переменных 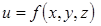называется множество точек пространства , в которых функция сохраняет своё значение.

Пример 10.2. Найдём область определения и линии уровня функции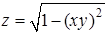  

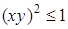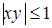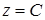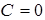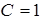Решение. Подкоренное выражение неотрицательно, значит,  или, что то же самое,  (см. рис. 5). Чтобы построить линии уровня, дадим функции некоторые значения , где  (так как область значений данной функции ). Например, возьмем , , . Построим графики этих функций. Из условия  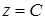следует, что , где . Линии уровня – семейство гипербол при 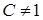 и прямые  при 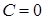(см. рис 6)

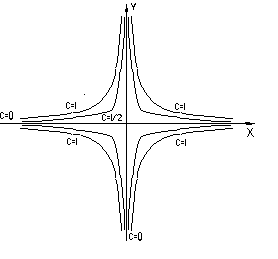
Рис. 5. Область определения              Рис. 6. Линии уровня

Пример 10.3. Найдём и построим линии уровня функции .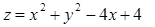
Решение. Областью определения данной функции является множество точек 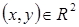. Условие линий уровня: z=C. Выделив в заданной функции полный квадрат: 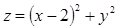, получим, что и 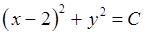. Это уравнения линий уровня, которые могут быть изображены на плоскости XOY как окружности с центром в точке 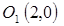и радиусами .(см. рис.8)

Заметим, что в условии задано уравнение параболоида, для которого линии уровня есть проекции на плоскость XOY линий его пересечения с плоскостями z=C (см. рис.7). На рис. 8 изображены линии уровня, соответствующие С=0, С=1, С=2 и С=4. При С=0 получаем точку 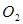 (соответствующая плоскость касается поверхности в точке ).

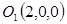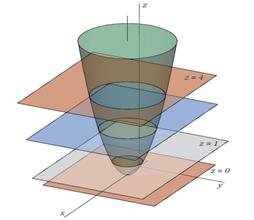
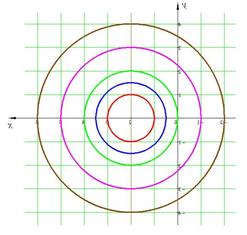
 Рис. 7. Сечение параболоида                      Рис. 8.  Линии уровня

плоскостями, параллельными XOY