И.В. Дубограй
О.В. Скуднева
ФУНКЦИИ НЕСКОЛЬКИХ
ПЕРЕМЕННЫХ
Учебно-
методическое пособие по дисциплине «Линейная алгебра и функции нескольких переменных».
для студентов всех специальностей факультета «Энергомашиностроение»
Москва
Издательство МГТУ им. Н. Э. Баумана
2019
Занятие 6 . Квадратичные формы, критерий Сильвестра. Преобразование матрицы квадратичной формы при переходе к новому базису.
Ауд.: [3], гл. 4: 4.218–4.225 (четн.) Дома: [3], гл. 4: 4.218–4.233 (неч.)
Часть 1. Квадратичная форма. Матрица квадратичной формы.
Рассмотрим конечномерное линейное пространство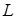 
с базисом 𝔅= 
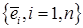. В этом базисе вектор 
.
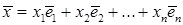Определение. Квадратичной формой, определённой для вектора 
, называется функция координат этого вектора, задаваемая как однородный многочлен второй степени относительно координат этого вектора 
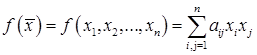, где коэффициенты 
.
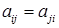То есть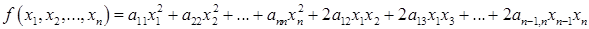 
.
Матрица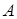 
, составленная из коэффициентов 
, называется матрицей квадратичной формы. Так как 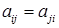, очевидно, что она является симметрической.
Если вектору поставить в соответствие матрицу – столбец из его координат, то квадратичную форму можно записать в матричном виде: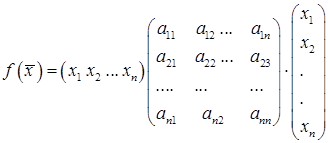 
, 
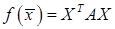
Матрицы 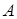и 
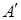квадратичной формы в двух различных базисах пространства связаны между собой так, что 
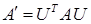, где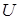 
– матрица перехода от исходного базиса к новому.
Определитель матрицы квадратичной формы называется её дискриминантом, а ранг этой матрицы – рангом квадратичной формы. Ранг квадратичной формы не зависит от выбора базиса (инвариантен относительно выбора базиса).
Если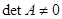 
, квадратичная форма называется невырожденной.
Пример 6.1. Составим матрицу квадратичной формы 
, вычислим её дискриминант и определим ранг.
Решение. При составлении матрицы квадратичной формы на главную диагональ ставим коэффициенты при квадратах переменных, а на остальные места – коэффициенты при попарных произведениях координат, делённые на 2. Квадратичную форму можно расписать, что удобно для составления её матрицы: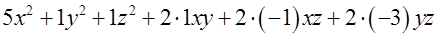 
. Расставив коэффициенты на соответствующие им места, получим матрицу
. Определитель этой матрицы равен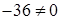 
, это значит, что матрица (а вместе с ней и квадратичная форма) невырожденная, и её ранг равен трём, то есть размерности пространства.
Пример 6.2. Дана матрица квадратичной формы: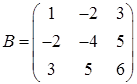 
. Составим саму квадратичную форму.
Решение. Воспользовавшись формулой 
, запишем квадратичную форму: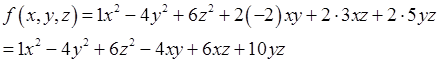 
Заметим, что определитель матрицы равен -96, её ранг равен 3, и данная квадратичная форма также является невырожденной.
Занятие 11 . Частные производные 1-го порядка ФНП. Частные производные высших порядков ФНП. Дифференциал первого и второго порядка ФНП.
Ауд.:[3]: 7.57, 7.60, 7.61, 7.63, 7.66, 7.87, 7.89, 7.91, 7.103, 7.105.
Дом: [3] 7.56, 7.58, 7.59, 7.62, 7.64, 7.67, 7.88, 7.90, 7.92, 7.102, 7.107.
И.В. Дубограй
О.В. Скуднева
ФУНКЦИИ НЕСКОЛЬКИХ
ПЕРЕМЕННЫХ
Учебно-
методическое пособие по дисциплине «Линейная алгебра и функции нескольких переменных».
для студентов всех специальностей факультета «Энергомашиностроение»
Москва
Издательство МГТУ им. Н. Э. Баумана
2019
Занятие 6 . Квадратичные формы, критерий Сильвестра. Преобразование матрицы квадратичной формы при переходе к новому базису.
Ауд.: [3], гл. 4: 4.218–4.225 (четн.) Дома: [3], гл. 4: 4.218–4.233 (неч.)
Часть 1. Квадратичная форма. Матрица квадратичной формы.
Рассмотрим конечномерное линейное пространство 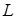с базисом 𝔅= 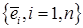. В этом базисе вектор .
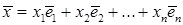Определение. Квадратичной формой, определённой для вектора 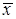, называется функция координат этого вектора, задаваемая как однородный многочлен второй степени относительно координат этого вектора 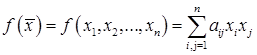, где коэффициенты .
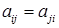То есть .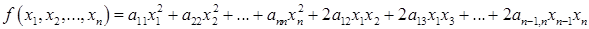
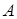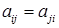Матрица , составленная из коэффициентов , называется матрицей квадратичной формы. Так как , очевидно, что она является симметрической.
Если вектору поставить в соответствие матрицу – столбец из его координат, то квадратичную форму можно записать в матричном виде: ,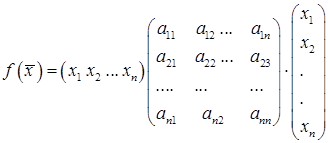
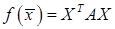
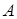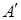Матрицы и квадратичной формы в двух различных базисах пространства связаны между собой так, что 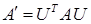, где 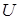– матрица перехода от исходного базиса к новому.
Определитель матрицы квадратичной формы называется её дискриминантом, а ранг этой матрицы – рангом квадратичной формы. Ранг квадратичной формы не зависит от выбора базиса (инвариантен относительно выбора базиса).
Если 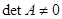, квадратичная форма называется невырожденной.
Пример 6.1. Составим матрицу квадратичной формы , вычислим её дискриминант и определим ранг.
Решение. При составлении матрицы квадратичной формы на главную диагональ ставим коэффициенты при квадратах переменных, а на остальные места – коэффициенты при попарных произведениях координат, делённые на 2. Квадратичную форму можно расписать, что удобно для составления её матрицы: 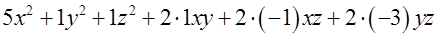. Расставив коэффициенты на соответствующие им места, получим матрицу
. Определитель этой матрицы равен 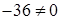, это значит, что матрица (а вместе с ней и квадратичная форма) невырожденная, и её ранг равен трём, то есть размерности пространства.
Пример 6.2. Дана матрица квадратичной формы: 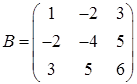. Составим саму квадратичную форму.
Решение. Воспользовавшись формулой , запишем квадратичную форму: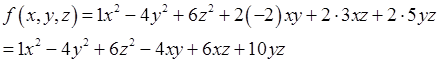
Заметим, что определитель матрицы равен -96, её ранг равен 3, и данная квадратичная форма также является невырожденной.
Дата: 2019-05-28, просмотров: 236.
