Определение. Если квадратичная форма содержит только квадраты переменных то такой её вид  называется каноническим.
называется каноническим.
Базис, в котором квадратичная форма имеет канонический вид, называется каноническим базисом.
Очевидно, что в каноническом базисе матрица квадратичной формы имеет диагональный вид 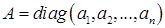 . Откуда следует, что ранг квадратичной формы совпадает с числом отличных от нуля коэффициентов
. Откуда следует, что ранг квадратичной формы совпадает с числом отличных от нуля коэффициентов  .
.
Канонический вид квадратичной формы, в котором коэффициенты равны одному из чисел  , называется нормальным видом.
, называется нормальным видом.
Метод Лагранжа заключается в последовательном выделении полных квадратов.
Пример 7.1. Привести квадратичную форму 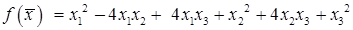 к каноническому виду, используя метод Лагранжа .
к каноническому виду, используя метод Лагранжа .
Решение: Выделим слагаемые, содержащие множитель 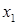 , и дополним их сумму до полного квадрата, тождественно преобразовав при этом квадратичную форму.
, и дополним их сумму до полного квадрата, тождественно преобразовав при этом квадратичную форму. 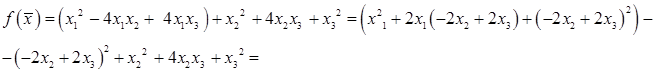
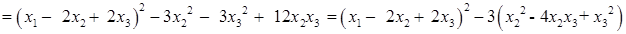 Теперь выделим полный квадрат во второй скобке, добавляя и вычитая
Теперь выделим полный квадрат во второй скобке, добавляя и вычитая 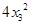 :
:
 . Таким образом, если обозначить
. Таким образом, если обозначить
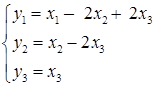 , то квадратичная форма примет канонический вид:
, то квадратичная форма примет канонический вид: 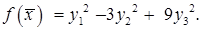
Связь между новыми 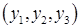 и старыми
и старыми  координатами вектора
координатами вектора  можно записать в матричном виде:
можно записать в матричном виде:  . Учитывая, что при переходе к новому базису
. Учитывая, что при переходе к новому базису 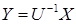 , имеем
, имеем  , где
, где 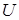 - матрица перехода (матрица преобразования).
- матрица перехода (матрица преобразования).
Вычислив её, получаем 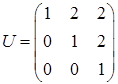 - матрица перехода к каноническому базису, в котором квадратичная форма имеет канонический вид
- матрица перехода к каноническому базису, в котором квадратичная форма имеет канонический вид 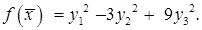
Замечание. Если в квадратичной форме (или на некотором этапе) вообще отсутствуют квадраты переменных, например,
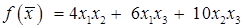 , то сделаем вспомогательную замену переменных:
, то сделаем вспомогательную замену переменных: 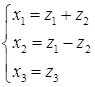 . При этом квадратичная форма принимает вид:
. При этом квадратичная форма принимает вид: 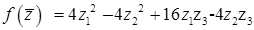 . Дальше действуем как в примере 7.1.
. Дальше действуем как в примере 7.1.
Очевидно, что канонический вид квадратичной формы неоднозначен.
Решить задачи 4.210,4.211. [3]
Часть 2. Приведение квадратичной формы к каноническому виду ортогональным преобразованием.
Матрица квадратичной формы симметрическая, поэтому существует ортогональное преобразование, которое приводит эту матрицу к диагональному виду, а следовательно, саму квадратичную форму к каноническому виду.
Пример 7.2. Привести к каноническому виду ортогональным преобразованием квадратичную форму
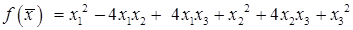 .
.
Решение. Составим матрицу квадратичной формы 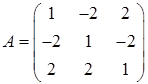 .
.
Решим характеристическое уравнение  . Оно имеет корни
. Оно имеет корни  (простой) и
(простой) и 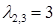 (кратности 2).
(кратности 2).
Корню  соответствует нормированный собственный вектор
соответствует нормированный собственный вектор 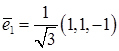 .
.
Корням 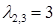 соответствует двумерное пространство собственных векторов
соответствует двумерное пространство собственных векторов  . Выбрав
. Выбрав 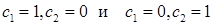 , получим
, получим 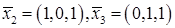 .
.
Так как 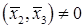 , пронормируем систему
, пронормируем систему 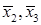 , и получим
, и получим  . В ортонормированном базисе
. В ортонормированном базисе 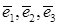 матрица квадратичной формы принимает диагональный вид:
матрица квадратичной формы принимает диагональный вид: 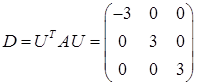 (где матрица перехода, составленная из координат ортонормированных собственных векторов,
(где матрица перехода, составленная из координат ортонормированных собственных векторов,  ортогональна, т.е.
ортогональна, т.е.  ).
).
Базис 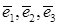 является для квадратичной формы каноническим, форма в этом базисе имеет вид
является для квадратичной формы каноническим, форма в этом базисе имеет вид 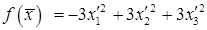 , где
, где
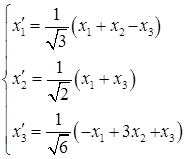 - линейное ортогональное преобразование координат, приводящее квадратичную форму к каноническому виду. Эта связь координат следует из того, что при переходе к новому базису с матрицей перехода
- линейное ортогональное преобразование координат, приводящее квадратичную форму к каноническому виду. Эта связь координат следует из того, что при переходе к новому базису с матрицей перехода 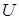 координаты вектора
координаты вектора  в этих базисах связаны формулой
в этих базисах связаны формулой 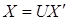 или
или 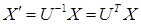 .
.
Дата: 2019-05-28, просмотров: 412.