Определение. Пусть задано уравнение 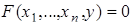 . Если точка
. Если точка 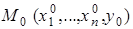 и уравнение
и уравнение  определяют в некоторой окрестности точки
определяют в некоторой окрестности точки 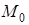 однозначную функцию
однозначную функцию  , то говорят, что уравнение
, то говорят, что уравнение  задает неявную функцию.
задает неявную функцию.
Теорема. Пусть функция 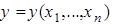 задана неявно уравнением
задана неявно уравнением  , где
, где 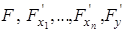 непрерывны в некоторой окрестности точки
непрерывны в некоторой окрестности точки 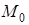 , причем
, причем 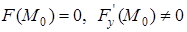 . Тогда
. Тогда 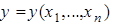 имеет в точке
имеет в точке 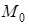 все частные производные и
все частные производные и 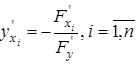
Пример 12.4. Найдём частные производные 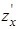 и
и 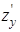 для функции, заданной уравнением
для функции, заданной уравнением 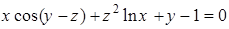 .
.
Решение. Введем обозначение 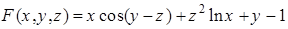 . Найдем
. Найдем 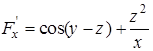 ,
,  ,
, 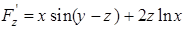 . Тогда
. Тогда 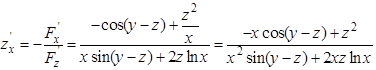 ;
;  Пример 12.5. Найдём полный дифференциал неявной функции
Пример 12.5. Найдём полный дифференциал неявной функции  , заданной уравнением
, заданной уравнением  .
.
Решение. Используя свойства дифференциала (те же, что и для функции одной переменной), вычислим полные дифференциалы левой и правой частей заданного равенства.
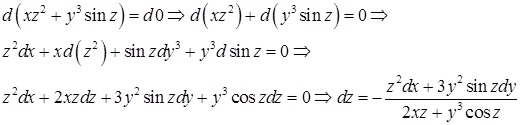
Часть 3. Производная по направлению. Градиент функции. Рассмотрим функцию  , дифференцируемую в некоторой области
, дифференцируемую в некоторой области 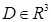 . В точке
. В точке  дадим приращение переменным
дадим приращение переменным  так, чтобы точка
так, чтобы точка 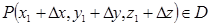 . Пусть вектор
. Пусть вектор 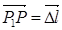 , его длина
, его длина 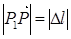 ,
, 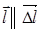 .
.
Определение. Производной функции 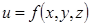 в точке
в точке 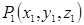 по направлению вектора
по направлению вектора 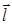 называется предел отношения приращения функции, соответствующего приращению
называется предел отношения приращения функции, соответствующего приращению 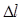 , к самому
, к самому  при условии его стремления к нулю:
при условии его стремления к нулю: 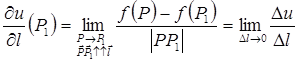 .
.
Если функция 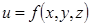 дифференцируема в точках некоторой области, то в этих точках производная вычисляется по следующей формуле:
дифференцируема в точках некоторой области, то в этих точках производная вычисляется по следующей формуле: 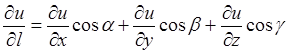 , где
, где 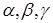 – углы, образуемые вектором
– углы, образуемые вектором 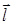 с соответствующими осями координат.
с соответствующими осями координат.
Если  , то
, то 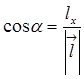 ,
, 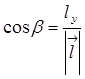 ,
,  .
.
Направляющие косинусы вектора  удовлетворяют равенству:
удовлетворяют равенству: 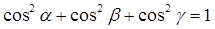 .
.
Для функции двух переменных 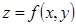 производная по направлению вычисляется по формуле
производная по направлению вычисляется по формуле 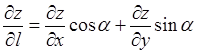 , т. к.
, т. к. 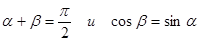 .
.
Производная по направлению в точке есть скорость изменения функции в данном направлении.
Определение. Градиентом функции 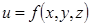 в произвольной точке области, где существуют частные производные этой функции, называется вектор,
в произвольной точке области, где существуют частные производные этой функции, называется вектор,
координатами которого являются соответствующие частные производные данной функции. 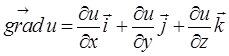 .
.
Соответственно, для  градиентом называется вектор
градиентом называется вектор 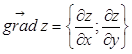 .
.
Замечания. 1. Вектор 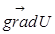 в данной точке указывает направление наибольшего роста функции
в данной точке указывает направление наибольшего роста функции 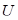 в этой точке. При этом наибольшее значение производной по направлению в точке M принимает значение
в этой точке. При этом наибольшее значение производной по направлению в точке M принимает значение
наиб. 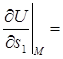
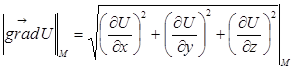 , когда
, когда 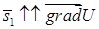 .
.
2. Градиент функции трёх (двух) переменных в точке М ортогонален к поверхности (линии) уровня, проходящей через точку М.
Пример 12.6. Найдём производную функции 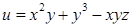 в точке
в точке 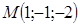 по направлению от неё к точке
по направлению от неё к точке  .
.
Решение. Производная функции  вычисляется по формуле
вычисляется по формуле 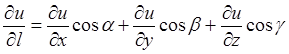 . Найдём частные производные функции в точке М:
. Найдём частные производные функции в точке М: 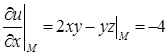 ,
, 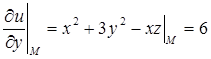 .
. 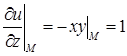
В качестве вектора направления возьмём вектор 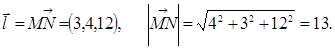 Тогда направляющие косинусы:
Тогда направляющие косинусы: 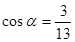 ,
, 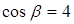 ,
, 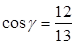 . Подставляем найденные величины в формулу и получаем:
. Подставляем найденные величины в формулу и получаем:  .
.
Ответ: 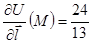 .
.
Замечание. Т.к.  функция в данном направлении возрастает.
функция в данном направлении возрастает.
Пример 12.7. Найдём наибольшее значение производной по направлению для функции 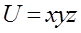 в точке
в точке  .
.
Решение. Известно, что направление наибольшего возрастания функции указывает вектор градиента. 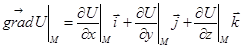 .
.
Вычислим значения частных производных в точке M: 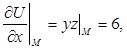
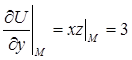
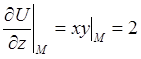
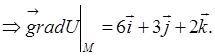
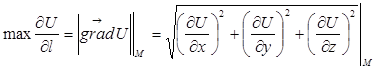 Отсюда следует, что
Отсюда следует, что 
Это значение достигается в направлении вектора 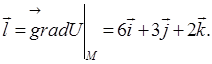
Ответ: 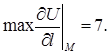
Пример 12.8. Найдём 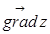 в точке
в точке 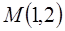 и линию уровня, проходящую через эту точку, для функции
и линию уровня, проходящую через эту точку, для функции 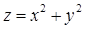 . Убедимся в их ортогональности.
. Убедимся в их ортогональности.
Решение. а) По определению, 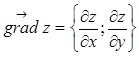 . Вычислим частные производные функции z в точке М:
. Вычислим частные производные функции z в точке М:  ;
;  .
.
Отсюда следует, что 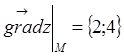 .
.
б) Для отыскания линии уровня положим z=C. Тогда  .Это уравнения окружностей. Для линии уровня, проходящей через точку
.Это уравнения окружностей. Для линии уровня, проходящей через точку 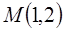 , выполняется условие
, выполняется условие  . То есть ей соответствует значение
. То есть ей соответствует значение 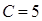 . Отсюда следует, что уравнение искомой линии уровня
. Отсюда следует, что уравнение искомой линии уровня  .
.
Убедимся в том, что в точке 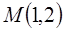 вектор
вектор 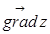 ортогонален к найденной линии уровня, то есть он перпендикулярен касательной к окружности
ортогонален к найденной линии уровня, то есть он перпендикулярен касательной к окружности 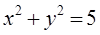 в точке М. Тангенс угла
в точке М. Тангенс угла  наклона касательной к окружности в точке М:
наклона касательной к окружности в точке М: 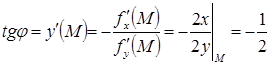 . Угол наклона
. Угол наклона 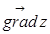 к положительному направлению оси OX обозначим ψ:
к положительному направлению оси OX обозначим ψ:
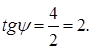 Из формулы
Из формулы  следует, что , т.к.
следует, что , т.к. 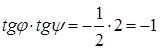 ,
, 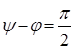 , ч. т. д.
, ч. т. д.
Ответ:  ,
, 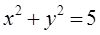 .
.
Дата: 2019-05-28, просмотров: 343.