Рассмотрим ФНП , которая имеет частные производные  во всех точках 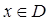. Эти производные в свою очередь есть новые ФНП, определённые в некоторой области .

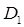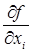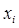Определение. Если функция  имеет частную производную по переменной , то эта производная называется производной второго порядка функции  по переменным  и .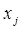

Обозначение: ; .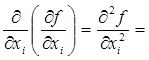

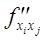Аналогично определяются производные более высокого порядка.

Смешанная производная k-ого порядка в точке P функции, которая непрерывна в окрестности этой точки вместе со своими частными производными до k-ого порядка включительно, не зависит от порядка дифференцирования. В частности, если функция 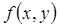 непрерывна вместе со своими частными производными до второго порядка включительно в окрестности точки, то в этой точке

.

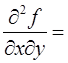
Пример 11.2.  Для функции 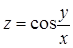 убедиться, что .

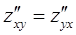Решение. Вычислим производные первого порядка.

,   .

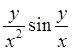Вычислим далее производные от полученных функций, чтобы получить смешанные производные 2 – ого порядка.

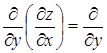
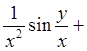
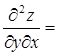
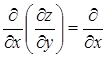
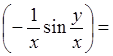
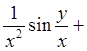
Получили 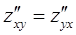, что и требовалось доказать.

Часть 3 . Дифференциал первого и второго порядка ФНП. Определение. Полным приращением функции 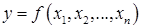, соответствующим приращениям аргументов  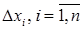называется разность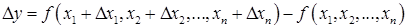  

Определение. Функция 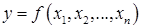, определённая в некоторой окрестности точки  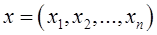называется дифференцируемой в ней, если существуют такие числа 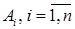, что в этой точке полное приращение функции может быть представлено в ви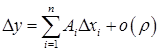де , где 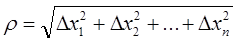,  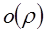бесконечно малая более высокого порядка, чем каждое .

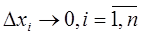Определение. Полным дифференциалом функции  называется главная часть полного приращения этой функции, линейная относительно приращений аргументов, т. е.

Дифференциалы независимых переменных совпадают с их приращениями, т. е. …, .

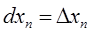Если функция дифференцируема в точке P, то числа . .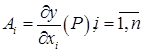

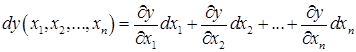В частности, для : .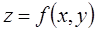

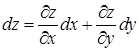Для    .

Правила дифференцирования:

Пример 11.3. Найдём полный дифференциал функции .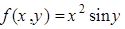

Решение. Вычислим частные производные данной функции: 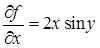, . Подставим их в формулу 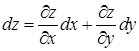, где 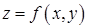, и получим ответ: .

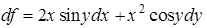Замечание. Для дифференцируемой в точке ФНП   её полное приращение 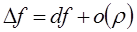. Тогда с точностью до бесконечно малой более высокого порядка относительно приращений аргументов (или ) верно следующее приближённое равенство: 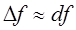. Это можно использовать для приближённых вычислений значений ФНП.

Пример 11.4. Используя дифференциал функции двух переменных, вычислим приближённо число .

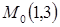Решение. Будем считать, что искомое число есть значение функции  в точке   с координатами . В соседней точке  значение функции легко вычисляется: 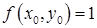, где .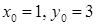

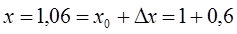
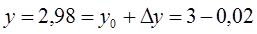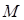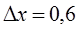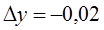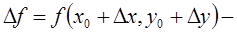
. Таким образом, при переходе из точки   в точку  координаты получают приращения , . 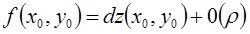, 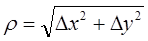. Отсюда .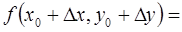

Вычислим : , . .

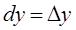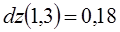Ответ: .

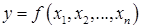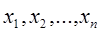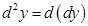Определение. Дифференциалом второго порядка функции  называется дифференциал от её полного дифференциала (или дифференциала 1-го порядка), рассматриваемого как функция переменных  при фиксированных значениях ,  …, .Обозначается .Дифференциал n – ого порядка: .

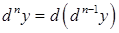Имеет место символическая формула, которая формально раскрывается по биномиальному закону: .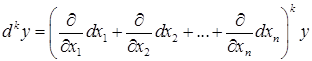

Например, для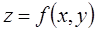  

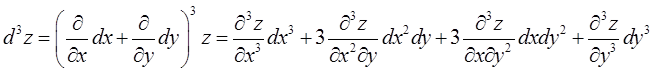
Пример 11.5. Найдём 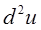 для функции  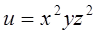в точке М(1,1,1).

Решение.

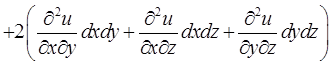
Вычисляем все частные производные второго порядка в точке М:

,  ,  ,

, ,

, , .

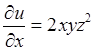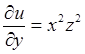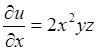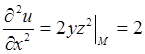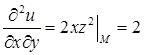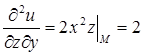Ответ: .