Теорема. Если функции 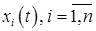 дифференцируемы в точке
дифференцируемы в точке 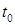 , в которой
, в которой 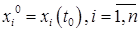 , а ФНП
, а ФНП 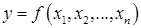 - дифференцируема в точке
- дифференцируема в точке 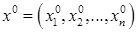 , то сложная функция
, то сложная функция 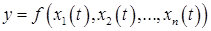 дифференцируема в точке
дифференцируема в точке 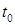 и имеет производную
и имеет производную 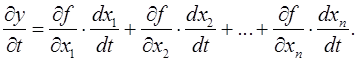
Чтобы составить формулу для вычисления производной от сложно заданной функции, полезно предварительно нарисовать схему зависимости заданной функции от всех переменных. По ней легко прослеживаются все связи. Рассмотрим несколько вариантов задания сложной функции. 1. Если 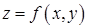 , где
, где  , то функция
, то функция 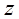 имеет непосредственно две частные производные
имеет непосредственно две частные производные 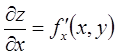 и
и 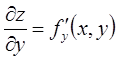 . А если учесть, что
. А если учесть, что 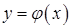 , то
, то 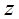 , как функция одной переменной
, как функция одной переменной  , имеет полную производную
, имеет полную производную 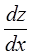 .
. 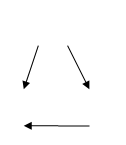 Чтобы составить формулу для вычисления
Чтобы составить формулу для вычисления 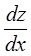 , построим схему зависимости z от своих переменных. По этой схеме составляем формулу
, построим схему зависимости z от своих переменных. По этой схеме составляем формулу  . Здесь учтены все варианты зависимости функции z от переменной
. Здесь учтены все варианты зависимости функции z от переменной  .
.
Замечание. Обратите внимание на обозначения производных. 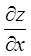 - частная производная функции, которая вычисляется при условии, что переменная
- частная производная функции, которая вычисляется при условии, что переменная  не меняется;
не меняется;
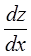 и
и  - полные производные от функций, зависящих только от одной переменной x.
- полные производные от функций, зависящих только от одной переменной x.
2. Пусть  , где
, где 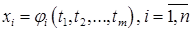 . Схема зависимости и формулы для вычисления частных производных
. Схема зависимости и формулы для вычисления частных производных  выглядят так:
выглядят так:

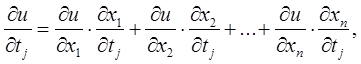
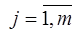
Пример 12.1. Найдём частные производные от сложно заданной функции 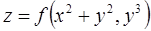 .
.
Решение. Представим функцию следующим образом: пусть  , где
, где  . Построим схему зависимости функции z от всех переменных и по ней составим формулы для вычисления
. Построим схему зависимости функции z от всех переменных и по ней составим формулы для вычисления 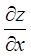 и
и  .
.
 По схеме видим, что функция
По схеме видим, что функция 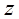 зависит от переменной
зависит от переменной 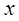 , которая связана только с
, которая связана только с 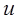 .
.
Как бы от 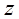 к
к 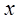 можно попасть только по одному «пути», сделав два «шага» от
можно попасть только по одному «пути», сделав два «шага» от 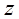 к
к  и от
и от  к
к  .
.
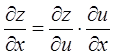 ,
, 
По схеме от 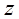 к
к  можно попасть или через
можно попасть или через 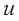 , сделав два «шага», или через
, сделав два «шага», или через 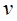 , сделав тоже два «шага».
, сделав тоже два «шага».
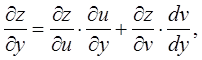
 Обратите внимание на обозначение производных.
Обратите внимание на обозначение производных. 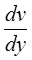 - полная производная от
- полная производная от 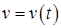 , т.к.
, т.к.  зависит от одной переменой
зависит от одной переменой  .
.
При вычислении производных высших порядков следует помнить, что любая частная производная зависит от тех же переменных, что и данная функция, причём по той же схеме.
Пример 12.2. Убедимся, что функция 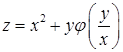 удовлетворяет уравнению
удовлетворяет уравнению 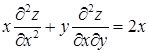 .
.
Решение. Для сложной функции 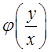 введём переменную
введём переменную 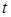 так, что
так, что  . Если
. Если 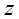 удовлетворяет данному уравнению, то подстановка частных производных в это уравнение приведёт его к тождественному равенству. Построим схему зависимости функции
удовлетворяет данному уравнению, то подстановка частных производных в это уравнение приведёт его к тождественному равенству. Построим схему зависимости функции  от переменных, и, составив формулу для вычисления
от переменных, и, составив формулу для вычисления 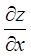 , найдём эту производную:
, найдём эту производную:

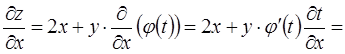
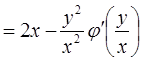 .
.
 Схема зависимости
Схема зависимости 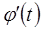 от переменных выглядит аналогично.
от переменных выглядит аналогично.


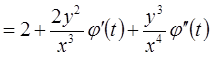 ,т.к.
,т.к.  .
. 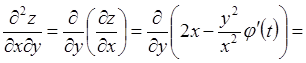

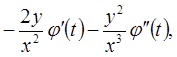 т.к.
т.к. 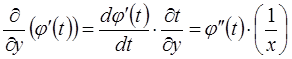 .
.
Подставляем найденные 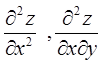 в уравнение:
в уравнение:

После упрощения получаем  , ч.т.д.
, ч.т.д.
Часть 2 . Дифференциал сложной функции. Инвариантность полного дифференциала ФНП.
Если 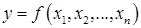 , то её полный дифференциал
, то её полный дифференциал  .
.
Эта форма записи сохраняется и в случае, если 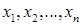 являются не только независимыми переменными, но и функциями других независимых переменных. Если
являются не только независимыми переменными, но и функциями других независимых переменных. Если  - сложная функция, где
- сложная функция, где 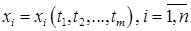 , то
, то
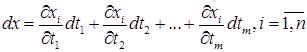 . Подставив все
. Подставив все 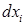 в выражение полного дифференциала
в выражение полного дифференциала  , получим после преобразования
, получим после преобразования 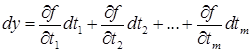 . То есть выражение
. То есть выражение  имеет тот же вид, что исходное. Отсюда следует, что полный дифференциал ФНП не зависит от того, являются ли переменные
имеет тот же вид, что исходное. Отсюда следует, что полный дифференциал ФНП не зависит от того, являются ли переменные  независимыми или зависят от других переменных. (Свойство инвариантности полного дифференциала относительно переменных.) Дифференциал высшего порядка не обладает свойством инвариантности.
независимыми или зависят от других переменных. (Свойство инвариантности полного дифференциала относительно переменных.) Дифференциал высшего порядка не обладает свойством инвариантности.
Пример 12.3. Найдём полный дифференциал сложно заданной функции  .
.
Решение. Пусть  . Тогда функция
. Тогда функция 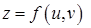 и её полный дифференциал
и её полный дифференциал 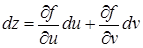 . При этом
. При этом 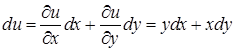 и
и 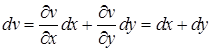 . Подставив найденные
. Подставив найденные 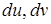 в формулу для
в формулу для 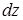 , получим ответ:
, получим ответ: 
Дата: 2019-05-28, просмотров: 321.