Задание 121-140. 1. В условии данной задачи необходимо: а). Перейти к вариационному ряду, и построить полигон частот; б). Найти выборочную среднюю, выборочную дисперсию, исправленную выборочную дисперсию, исправленное выборочное среднеквадратическое отклонение случайной величины Х; в). Построить доверительный интервал для генеральной средней и генерального среднеквадратического отклонения с заданным уровнем доверительной вероятности γ=0,95; г). Используя критерий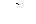 
Пирсона при уровне значимости a=0,05 проверить гипотезу о том, что случайная величина X– распределена по нормальному закону. Построить на одном графике гистограмму эмпирического распределения и соответствующую нормальную кривую.
121. Для проверки качества поступившей партии зерна по схеме собственно-случайной бесповторной выборки произведено 10%-ное обследование. В результате анализа установлено следующее распределение данных о влажности зерна:
| Процент влажности | Менее 8 | 8–10 | 10–12 | 12–14 | 14–16 | 16–18 | 18–20 | Более 20 |
| Число проб | 7 | 15 | 30 | 35 | 25 | 18 | 7 | 3 |
122. По схеме собственно-случайной бесповторной выборки проведено 5%-ное обследование вкладов в Сбербанк одного из городов. Результаты обследования 150 вкладов представлены в таблице:
| Размер вклада, тыс. руб. | Менее 40 | 40–60 | 60–80 | 80–100 | 100–120 | 120–140 | Более 140 |
| Число вкладов | 6 | 17 | 35 | 43 | 28 | 13 | 8 |
123.По схеме собственно-случайной бесповторной выборки проведено 10%-ное обследование предприятий одной из отраслей экономики в отчетном году. Результаты обследования представлены в таблице:
| Выпуск продукции, млн.руб. | Менее 30 | 30–40 | 40–50 | 50–60 | 60–70 | 70–80 | 80–90 | Более 90 |
| Число предприятий | 6 | 9 | 19 | 29 | 21 | 9 | 5 | 2 |
124. По схеме собственно-случайной бесповторной выборки проведено 10%-ное обследование предприятий одной из отраслей экономики в отчетном году. Результаты обследования представлены в таблице:
| Выпуск продукции, млн.руб. | Менее 30 | 30–40 | 40–50 | 50–60 | 60–70 | 70–80 | 80–90 | Более 90 |
| Число предприятий | 6 | 9 | 19 | 29 | 21 | 9 | 5 | 2 |
125. Данные об урожайности зерновых культур в некотором регионе получены с помощью собственно-случайной бесповторной выборки. Результаты обследования 100 предприятий из 1000 приведены в таблице:
| Урожайность, ц/га | 20–30 | 30–40 | 40–50 | 50–60 | 60–70 | 70–80 | 80–90 | 90–100 |
| Число предприятий | 6 | 9 | 19 | 29 | 21 | 9 | 5 | 2 |
126. В результате выборочного обследования 100 предприятий из 1000 по схеме собственно-случайной бесповторной выборки, получено следующее распределение предприятий по росту производительности труда (в процентах по отношению к предыдущему году):
| Рост производительности труда, % | 13–17 | 17–21 | 21–25 | 25–29 | 29–33 | 33–37 |
| Число предприятий | 6 | 20 | 24 | 29 | 11 | 10 |
127. Для нахождения средней цены продовольственной корзины из 1000 городов России по схеме собственно-случайной бесповторной выборки отобрали 100 городов. Полученные данные представлены в таблице:
| Стоимость продовольственной корзины, тыс. руб. | Менее 1,0 | 1,0–1,2 | 1,2–1,4 | 1,4–1,6 | Более 1,6 |
| Число городов | 11 | 27 | 34 | 21 | 7 |
128.Данные о продолжительности телефонных разговоров, отобранные по схеме собственно-случайной бесповторной выборки, приведены в таблице:
| Время, мин | 1,5–2,5 | 2,5–3,5 | 3,5–4,5 | 4,5–5,5 | 5,5–6,5 | 6,5–7,5 | 7,5–8,5 | 8,5–9,5 | 9,5–10,5 |
| Число разговоров | 3 | 4 | 9 | 14 | 37 | 12 | 8 | 8 | 5 |
129. Для нахождения среднего времени прорастания семян из большой партии по схеме собственно-случайной бесповторной выборки было отобрано 200 семян. Распределение семян по времени их прорастания представлено в таблице:
| Время прорастания, дни | Менее 4 | 4–6 | 6–8 | 8–10 | 10–12 | 12–14 | Более 14 |
| Число семян | 2 | 14 | 55 | 73 | 38 | 10 | 8 |
130. По схеме собственно-случайной бесповторной выборки из 1500 участников соревнования было отобрано 100 человек. Их распределение по числу набранных баллов дано в таблице:
| Число набранных баллов | 52–56 | 56–60 | 60–64 | 64–68 | 68–72 | 72–76 |
| Число участников | 9 | 11 | 19 | 30 | 21 | 10 |
131. Для нахождения средней стоимости компьютера определенной комплектации из 500 компьютерных магазинов региона по схеме собственно-случайной бесповторной выборки было отобрано 100 магазинов. Распределение компьютеров по их стоимости представлено в таблице:
| Стоимость компьютера, тыс. руб. | 10–12 | 12–14 | 14–16 | 16–18 | 18–20 | 20–22 |
| Число магазинов | 3 | 13 | 36 | 26 | 14 | 8 |
132. С целью определения средней продолжительности обслуживания клиентов в пенсионном фонде, число клиентов которого очень велико, по схеме собственно-случайной бесповторной выборки проведено обследование 100 клиентов. Результаты обследования представлены в таблице:
| Время обслуживания, мин. | Менее 2 | 2–4 | 4–6 | 6–8 | 8–10 | 10–12 | Более 12 |
| Число клиентов | 6 | 10 | 21 | 39 | 15 | 6 | 3 |
133. Из 1560 сотрудников предприятия по схеме собственно случайной бесповторной выборки отобрано 100 человек для получения статистических данных о пребывании на больничном листе в течение года. Полученные данные представлены в таблице:
| Количество дней пребы-вания на больничном листе | Менее 3 | 3–5 | 5–7 | 7–9 | 9–11 | Более 11 |
| Число сотрудников | 6 | 13 | 24 | 39 | 8 | 10 |
134. В некотором городе по схеме собственно случайной бесповторной выборки было обследовано 80 магазинов розничной торговли из 2500 с целью изучения объема розничного товарооборота. Получены следующие данные:
| Товарооборот, у.е. | Менее 60 | 60–70 | 70–80 | 80–90 | 90–100 | Более 100 |
| Число магазинов | 12 | 19 | 23 | 18 | 5 | 3 |
135. В результате выборочного обследования российских автомобилей, обслуживающихся в автосервисе по гарантии, по схеме собственно-случайной бесповторной выборки из 280 автомобилей были отобраны 60. Полученные данные о пробеге автомобилей с момента покупки до первого гарантийного ремонта представлены в таблице:
| Пробег, тыс.км | Менее 1 | 1–2 | 2–3 | 3–4 | 4–5 | 5–6 | Более 6 |
| Число автомобилей | 3 | 5 | 9 | 16 | 13 | 8 | 6 |
136. В филиале заочного вуза обучается 2000 студентов. Для изучения стажа работы студентов по специальности по схеме собственно случайной бесповторной выборки отобрано 100 студентов. Полученные данные о стаже работы студентов по специальности представлены в таблице:
| Стаж работы по специальности, лет | Менее 2 | 2–4 | 4–6 | 6–8 | 8–10 | 10–12 | Более 12 |
| Количество студентов | 10 | 19 | 24 | 27 | 12 | 5 | 3 |
137. Имеются выборочные данные о распределении вкладчиков по размеру вклада в Сбербанке города:
| Размер вклада, тыс. руб. | До 40 | 40–60 | 60–80 | 80–100 | Свыше 100 |
| Число вкладов | 32 | 56 | 92 | 120 | 100 |
138. В результате выборочного обследования 100 предприятий региона из 500 по схеме собственно случайной бесповторной выборки получено следующее распределение снижения затрат на производство продукции в процентах к предыдущему году:
| Процент снижения затрат (%) | 4–6 | 6–8 | 8–10 | 10–12 | 12–14 | 14–16 |
| Число предприятий | 6 | 20 | 31 | 24 | 13 | 6 |
139. С целью изучения дневной выборки ткани (м) ткачихами комбината по схеме собственно-случайной бесповторной выборки было отобрано 100 ткачих из 2000. Результаты обследования представлены в таблице:
| Дневная выработка, м | Менее 55 | 55–65 | 65–75 | 75–85 | 85–95 | 95–105 | Более 105 |
| Число ткачих | 8 | 7 | 15 | 35 | 20 | 8 | 7 |
140. Для планирования бюджета предприятия на следующий год было проведено выборочное обследование использования амортизационного фонда. По схеме собственно- случайной бесповторной выборки из 500 выплат были отобраны 100 и получены следующие данные:
| Величина выплаты (руб.) | Менее 1000 | 1000–2000 | 2000–3000 | 3000–4000 | 4000–5000 | 5000–6000 |
| Число выплат | 3 | 13 | 33 | 26 | 17 | 8 |
Задачи № 141-160. Необходимо:
1. Вычислить условные средние 
и 
и построить эмпирические линии регрессии.
2. предполагая, что между переменными Х и Y существует линейная корреляционная зависимость:
а) найти уравнения прямых регрессии и построить их графики на одном чертеже с эмпирическими линиями регрессии;
б) вычислить коэффициент корреляции на уровне значимости 0,05, оценить его значимость и сделать вывод о тесноте и направлении связи между переменными Х и Y;
в) используя соответствующее уравнение регрессии, определить количество примесей в драгоценном изделии, если его стоимость составляет 25 тыс. руб.
141. Распределение 60 предприятий по затратам рабочего времени X (тыс. человеко-дней (чел. дн.)) и выпуску продукции Y (млн. руб.) представлены в таблице:
 y
x
| 30–40 | 40–50 | 50–60 | 60–70 | 70–80 | Итого: |
| 10–25 | 1 | 3 | 2 | 6 | ||
| 25–40 | 3 | 6 | 4 | 1 | 14 | |
| 40–55 | 3 | 7 | 6 | 1 | 17 | |
| 55–70 | 1 | 6 | 4 | 4 | 15 | |
| 70–85 | 2 | 5 | 1 | 8 | ||
| Итого: | 4 | 13 | 21 | 16 | 6 | 60 |
142. Распределение 50 предприятий по стоимости основных производственных фондов X (млн. руб.) и стоимости произведенной продукции Y (млн. руб.) представлены в таблице:
| y
x
| 15–20 | 20–25 | 25–30 | 30–35 | 35–40 | 40–45 | Итого: |
| 20–30 | 1 | 4 | 2 | 7 | |||
| 30–40 | 2 | 4 | 5 | 2 | 13 | ||
| 40–50 | 5 | 6 | 2 | 1 | 14 | ||
| 50–60 | 1 | 3 | 3 | 4 | 11 | ||
| 60–70 | 1 | 3 | 1 | 5 | |||
| Итого: | 3 | 13 | 14 | 8 | 7 | 5 | 50 |
143. Распределение 80 литейных цехов машиностроительных заводов по степени компьютеризации процессов производства X (%) и производственным затратам Y (млн. руб.) представлено в таблице:
| y x | 5–6 | 6–7 | 7–8 | 8–9 | 9–10 | Итого: |
| 10–20 | 2 | 4 | 2 | 8 | ||
| 20–30 | 1 | 5 | 3 | 9 | ||
| 30–40 | 2 | 3 | 7 | 1 | 13 | |
| 40–50 | 4 | 2 | 10 | 2 | 18 | |
| 50–60 | 1 | 3 | 11 | 2 | 17 | |
| 60–70 | 2 | 8 | 5 | 15 | ||
| Итого: | 7 | 15 | 32 | 20 | 6 | 80 |
144. Распределение 80 предприятий, выпускающих однотипную продукцию, по количеству реализованных товаров X (тыс. ед.) и цене на производимые товары Y (тыс. руб. за ед. продукции) представлено в таблице:
| y x | 10–20 | 20–30 | 30–40 | 40–50 | 50–60 | Итого: |
| 60–70 | 3 | 3 | 6 | |||
| 70–80 | 1 | 5 | 4 | 10 | ||
| 80–90 | 2 | 7 | 7 | 1 | 17 | |
| 90–00 | 6 | 10 | 4 | 20 | ||
| 100–110 | 2 | 7 | 8 | 2 | 19 | |
| 110–120 | 4 | 4 | 8 | |||
| Итого: | 6 | 19 | 26 | 21 | 8 | 80 |
145. Распределение 100 средних фермерских хозяйств по числу наемных рабочих X (чел.) и их средней месячной заработной плате на 1 человека Y (тыс. руб.) представлено в таблице:
| y x | 2 – 4 | 4 – 6 | 6 – 8 | 8 – 10 | 10 – 12 | Итого |
| 1–3 | 6 | 8 | 4 | 18 | ||
| 3–5 | 2 | 10 | 2 | 2 | 16 | |
| 5–7 | 2 | 6 | 8 | 2 | 18 | |
| 7–9 | 4 | 12 | 10 | 2 | 28 | |
| 9–11 | 10 | 6 | 4 | 20 | ||
| Итого | 16 | 26 | 38 | 14 | 6 | 100 |
146. Распределение 100 новых видов тарифов на сотовую связь всех известных мобильных систем X (ден. ед.) и выручка от них Y (ден. ед.) приводится в таблице:
| y x | 10 | 15 | 20 | 25 | 30 | 35 | Итого |
| 20 | 4 | 2 | 6 | ||||
| 30 | 5 | 3 | 8 | ||||
| 40 | 5 | 45 | 5 | 55 | |||
| 50 | 2 | 8 | 7 | 17 | |||
| 60 | 0 | 4 | 7 | 3 | 14 | ||
| Итого | 4 | 7 | 10 | 57 | 19 | 3 | 100 |
147. Распределение 50 курящих мужчин по количеству выкуриваемых в день сигарет X (штук) и продолжительности жизни Y (лет) представлено в таблице:
| y x | Менее 60 | 60–65 | 65–70 | 70 –75 | Более 75 | Итого |
| Менее 10 | 1 | 1 | 2 | 5 | 9 | |
| 10–20 | 1 | 2 | 2 | 3 | 8 | |
| 20–30 | 2 | 3 | 3 | 1 | 9 | |
| 30–40 | 4 | 5 | 2 | 1 | 12 | |
| Более 40 | 6 | 5 | 1 | 12 | ||
| Итого | 13 | 16 | 9 | 7 | 5 | 50 |
148. В таблице приведено распределение 120 коров по дневному надою Y (в кг) и по жирности X (в %):
| y x | 7 | 9 | 11 | 13 | 15 | Итого |
| 3,3 | 8 | 8 | ||||
| 3,5 | 2 | 16 | 8 | 26 | ||
| 3,7 | 4 | 16 | 10 | 2 | 32 | |
| 3,9 | 2 | 6 | 10 | 2 | 20 | |
| 4,1 | 8 | 6 | 20 | 34 | ||
| Итого | 10 | 16 | 48 | 36 | 10 | 120 |
149. Распределение 50 городов по численности населения X (тыс. чел.) и среднемесячному доходу на одного человека Y (тыс. руб.) представлено в таблице:
| y x | 2–3 | 3 – 4 | 4 – 5 | 5 – 6 | 6 – 7 | 7–8 | Итого |
| 0–50 | 1 | 1 | 3 | 5 | |||
| 50–100 | 2 | 5 | 1 | 8 | |||
| 100–150 | 1 | 1 | 6 | 2 | 2 | 12 | |
| 150–200 | 4 | 9 | 13 | ||||
| 200–250 Более 250 | 2 | 2 | 5 2 | 1 | 9 3 | ||
| Итого | 1 | 4 | 15 | 18 | 9 | 3 | 50 |
150. Распределение 50 предприятий пищевой промышленности по степени автоматизации производства Х (%) и росту производительности труда Y (%) представлено в таблице:
| у х | 5–9 | 9–13 | 13–17 | 17–21 | 21–25 | Итого |
| 15–21 | 3 | 2 | 1 | 6 | ||
| 21–27 | 1 | 2 | 3 | 2 | 8 | |
| 27–33 | 2 | 7 | 3 | 12 | ||
| 33–39 | 2 | 5 | 8 | 15 | ||
| 39–45 | 2 | 2 | 1 | 5 | ||
| 45–51 | 2 | 2 | 4 | |||
| Итого | 4 | 8 | 18 | 17 | 3 | 50 |
151. Распределение 110 образцов полимерных композиционных материалов по содержанию в них нефтешламов Х (%) и водопоглощению Y (%) представлено в таблице:
| у х | 15–25 | 25–35 | 35–45 | 45–55 | 55–65 | 65–75 | Итого |
| 5–15 | 17 | 4 | 21 | ||||
| 15–25 | 3 | 18 | 3 | 24 | |||
| 25–35 | 2 | 15 | 5 | 22 | |||
| 35–45 | 3 | 13 | 7 | 23 | |||
| 45–55 | 6 | 14 | 20 | ||||
| Итого | 20 | 24 | 21 | 18 | 13 | 14 | 110 |
152. Имеются следующие выборочные данные о рыночной стоимости квартир Y (тыс.у.е.) и их общей площади Х (кв.м) :
| у х | 13–18 | 18–23 | 23–28 | 28–33 | 33–38 | Итого |
| 33–49 | 4 | 2 | 1 | 7 | ||
| 49–65 | 2 | 6 | 4 | 1 | 13 | |
| 65–81 | 1 | 4 | 9 | 4 | 1 | 19 |
| 81–97 | 3 | 6 | 3 | 12 | ||
| 97–113 | 1 | 3 | 5 | 9 | ||
| Итого | 7 | 12 | 18 | 14 | 9 | 60 |
153. Распределение 60 банков по величине процентной ставки Х (%) и размеру выданных кредитов Y (млн.руб.) представлено в таблице:
| y х | 2–5 | 5–8 | 8–11 | 11–14 | 14–17 | Итого |
| 11–13 | 1 | 6 | 7 | |||
| 13–15 | 4 | 7 | 3 | 14 | ||
| 15–17 | 1 | 11 | 5 | 1 | 18 | |
| 17–19 | 4 | 5 | 2 | 11 | ||
| 19–21 | 8 | 2 | 10 | |||
| Итого | 12 | 8 | 17 | 13 | 10 | 60 |
154. Распределение 100 предприятий по количеству работников Y (чел.) и средней месячной надбавки к зарплате Х (%) представлено в таблице:
| у х | 10–20 | 20–30 | 30–40 | 40–50 | 50–60 | Итого |
| 7,5–12,5 | 6 | 4 | 10 | |||
| 12,5–17,5 | 6 | 6 | 2 | 14 | ||
| 17,5–22,5 | 10 | 2 | 12 | |||
| 22,5–27,5 | 3 | 6 | 8 | 2 | 19 | |
| 27,5–32,5 | 4 | 11 | 10 | 25 | ||
| 32,5–37,5 | 10 | 6 | 4 | 20 | ||
| Итого | 17 | 23 | 38 | 16 | 6 | 100 |
155. Распределение 50 предприятий по стоимости основных производственных фондов Х (млн.руб.) и стоимости произведенной продукции Y (млн.руб.) представлены в таблице:
| у х | 15–25 | 25–35 | 35–45 | 45–55 | 55–65 | 65–75 | Итого |
| 5–15 | 17 | 4 | 21 | ||||
| 15–25 | 3 | 18 | 3 | 24 | |||
| 25–35 | 2 | 15 | 5 | 22 | |||
| 35–45 | 3 | 13 | 7 | 23 | |||
| 45–55 | 6 | 14 | 20 | ||||
| Итого | 20 | 24 | 21 | 18 | 13 | 14 | 110 |
156. Распределение 60 предприятий по объему инвестиций в развитие производства Х (млн.руб.) и получаемой за год прибыли Y (млн.руб.) представлены в таблице:
| у х | 0–0,8 | 0,8–1,6 | 1,6–2,4 | 2,4–3,2 | 3,2–4,0 | Итого |
| 2–4 | 2 | 2 | 4 | |||
| 4–6 | 2 | 7 | 10 | 19 | ||
| 6–8 | 2 | 17 | 7 | 26 | ||
| 8–10 | 4 | 3 | 2 | 9 | ||
| 10–12 | 2 | 2 | ||||
| Итого | 4 | 11 | 31 | 10 | 4 | 60 |
157. Распределение 50 однотипных предприятий по основным фондам Х (млн.руб.) и себестоимости выпуска единицы продукции Y (млн.руб.) представлены в таблице:
| у х | 1 | 2 | 3 | 4 | 5 | Итого |
| 30–80 | 1 | 2 | 3 | 6 | ||
| 80–130 | 1 | 4 | 3 | 8 | ||
| 130–180 | 4 | 8 | 3 | 1 | 16 | |
| 180–230 | 2 | 5 | 4 | 11 | ||
| 230–280 | 3 | 4 | 2 | 9 | ||
| Итого | 5 | 13 | 16 | 9 | 7 | 50 |
158. Распределение 50 городов по численности населения Х (тыс. чел.) и среднемесячному доходу на одного человека Y (тыс. руб.) представлено в таблице:
| у х | 3–4 | 4–5 | 5–6 | 6–7 | 7–8 | Более 8 | Итого |
| 30–50 | 1 | 1 | 3 | 5 | |||
| 50–70 | 2 | 5 | 1 | 8 | |||
| 70–90 | 1 | 1 | 6 | 2 | 2 | 12 | |
| 90–110 | 4 | 9 | 13 | ||||
| 110–130 | 2 | 2 | 5 | 9 | |||
| Более 130 | 2 | 1 | 3 | ||||
| Итого: | 1 | 4 | 15 | 18 | 9 | 3 | 50 |
159. Распределение 70 банков по величине процентной ставки Х (%) и размеру выданных кредитов Y (млн.руб.) представлено в таблице:
| y х | 2–5 | 5–8 | 8–11 | 11–14 | 14–17 | Итого |
| 11–13 | 2 | 8 | 10 | |||
| 13–15 | 5 | 7 | 4 | 16 | ||
| 15–17 | 1 | 11 | 5 | 1 | 18 | |
| 17–19 | 4 | 5 | 2 | 11 | ||
| 19–21 | 10 | 5 | 15 | |||
| Итого | 14 | 11 | 18 | 14 | 13 | 70 |
160. Распределение 110 предприятий по количеству работников Y (чел.) и средней месячной надбавки к зарплате Х (%) представлено в таблице:
| у х | 10–20 | 20–30 | 30–40 | 40–50 | 50–60 | Итого |
| 7,5–12,5 | 9 | 6 | 15 | |||
| 12,5–17,5 | 6 | 6 | 2 | 14 | ||
| 17,5–22,5 | 11 | 3 | 14 | |||
| 22,5–27,5 | 3 | 6 | 8 | 2 | 19 | |
| 27,5–32,5 | 4 | 12 | 10 | 26 | ||
| 32,5–37,5 | 10 | 7 | 5 | 22 | ||
| Итого | 17 | 25 | 40 | 20 | 8 | 110 |
Вопросы для подготовки к зачету (3 семестр)
| Компетенция | Вопросы к зачету |
| ПК-22 Способностью использовать законы и методы математики, естественных, гуманитарных и экономических наук при решении профессиональных задач | 1. Элементы комбинаторики. 2. Испытания и события. Классификация событий. Примеры. 3. Понятие вероятности. Классическое определение вероятности события. Свойства вероятности. Полная группа событий. Противоположные события. 4. Понятие суммы событий. Теорема сложения вероятностей несовместных событий. 5. Понятие произведения событий. Теорема умножения вероятностей зависимых и независимых событий. 6. Повторные независимые испытания. Формула Бернулли. 7. Локальная и интегральная теорема Лапласа. Формула Пуассона 8. Понятие и виды случайной величины. Дискретная случайная величина. Примеры. Закон распределения д.с.в. 9. Математическое ожидание д.с.в. Вероятностный смысл М(х) Свойства М(х) 10. Определение дисперсии. Формула для вычисления Д(х). Свойства Д(х) 11. Определение функции распределения, ее свойства и график. 12. Непрерывная случайная величина. Функция распределения н.с.в и ее свойства. Вероятность попадания в заданный интервал. 13. Функция плотности распределения н.с.в и ее свойства. Вероятностный смысл плотности распределения. 14. Числовые характеристики непрерывной случайной величины 15. Нормальный закон распределения н.с.в. Числовые характеристики для нормального распределения. 16. Выборочный метод. Генеральная совокупность и выборка. Статистическое распределение выборки. Полигон и гистограмма. 17. Числовые характеристики статистического распределения. 18. Точечные и интервальные оценки статистического распределения. 19. Проверка гипотезы о законе распределения генеральной совокупности. Критерий Пирсона. 20. Исследование статистической зависимости двух случайных величин. Линейная регрессия и корреляция. |
Процедура оценивания зачета
Очная форма обучения
Согласно положению о текущем контроле и промежуточной аттестации студентов, ФГБОУ ВО «Государственный аграрный университет Северного Зауралья» принятого решением ученого совета от 4 апреля 2016 г. протокол № 10: «зачет служит формой аттестации по итогам выполнения и защиты студентами лабораторных и практических занятий. При условии успешной защиты всех лабораторных работ и практических занятий, предусмотренных рабочей программой дисциплины, выставляется оценка «Зачтено»».
Таким образом, по дисциплине «Математика» выставляется оценка «Зачтено», при условии посещения студентами занятий; успешного выполнения контрольных работ; защиты РГР; получения положительной оценки при собеседовании по темам, выносимым на самостоятельное обучение.
Если студент не выполнил условия программы дисциплины, то зачет проводится в форме теста, по результатам которого выставляется оценка «Зачтено» либо «Не зачтено» в зависимости от процента верно выполненных заданий. Метод тестирования - бумажный. Перед началом работы над тестами преподаватель проводит инструктаж, разъясняет порядок заполнения ответов, порядок проведения тестирования, оговаривает вопросы соблюдения дисциплины при тестировании.
Время начала и окончания тестирования фиксируется, нарушение временного регламента не допускается.
Во время проведения тестирования каждому студенту предоставляется отдельное место, которое организуется в соответствии с требованиями гарантированного индивидуального выполнения теста.
При неоднократном нарушении дисциплины тестируемый удаляется из аудитории.
В процессе прохождения тестирования студенту разрешается пользоваться только ручкой, калькулятором и тестовыми материалами.
Заочная форма обучения
По дисциплине «Математика» студенты заочной формы в третьем семестре сдают зачет. Зачет выставляется по результатам РГР, которая предусмотрена учебным планом при посещении всех лекционных и практических занятий. В противном случае, процедура сдачи зачета как у студентов очного отделения.
Критерии оценки
Студенту выдается вариант с зачетными тестовыми заданиями и предоставляется 60 минут на подготовку. В задание включено 40 тестовых вопросов по 8 из каждой темы, с возможными вариантами ответов, из которых необходимо выбрать правильный. Оценка выставляется:
«зачтено», если студент верно отвечает на 60-100% вопросов теста.
«не зачтено», если обучающийся допустил грубые ошибки и ответил верно менее чем на 60% вопросов теста.
Учебно-методическое и информационное обеспечение дисциплины
а) основная литература
2. Гмурман В.Е. Теория вероятностей и математическая статистика: Учеб. пособие / В.Е. Гмурман. – М.: Высшее образование, 2006 г
3. Гмурман В.Е. Руководство к решению задач по теори вероятностей и математической статистике: Учеб. пособие / В.Е. Гмурман. – М.: Высшее образование, 2006 г.
4. Соколов, Г.А., Гладких. Математическая статистика для вузов/ Г.А. Соколов, И.М. Гладких. – 2-е изд., исправл.- М.: Издательство «Экзамен», 2007
б) дополнительная литература
1. Гудыма А.П. Лабораторный практикум по математической статистике: методические указания и варианты индивидуальных заданий для выполнения расчетно-графических работ в 3-х частях, Тюмень 2000 г.
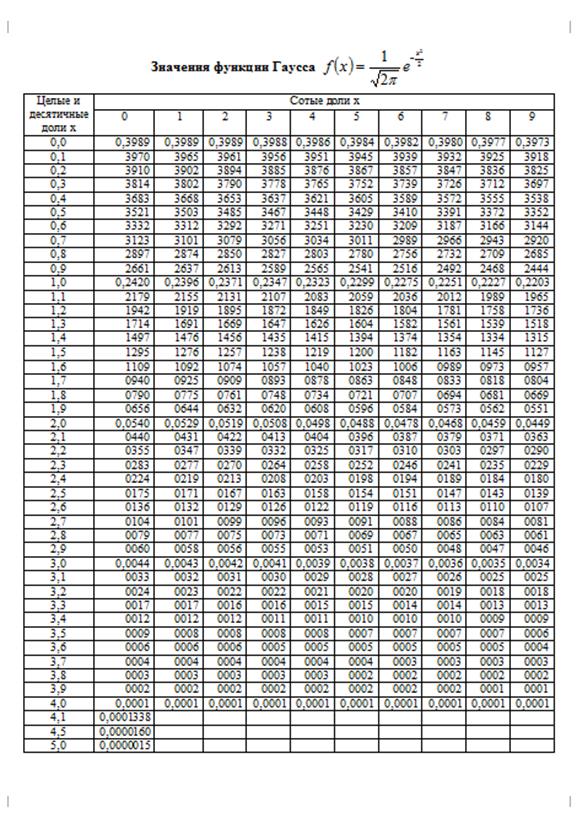
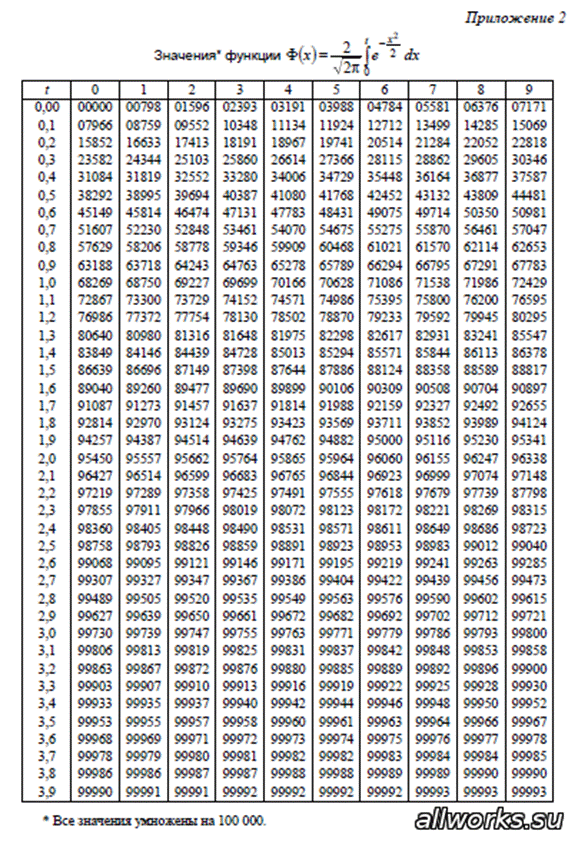
Приложение 1
Дата: 2019-05-28, просмотров: 633.
